2. 燕山大学 信息科学与工程学院, 河北 秦皇岛 066004;
3. 清华大学 电子工程系, 北京 100084;
4. 新乡学院 网络管理中心, 河南 新乡 453003
针对云服务系统中虚拟机可以迁移的特点,提出了服务台数量可变的M/M/m(t)系统模型.构造基于子任务队长过程和虚拟机数量变化过程的两维马尔可夫链,利用矩阵几何理论得到了该过程的稳态分布以及该系统的稳态性能指标.在考虑服务水平协议的前提下,给出了系统需要开启虚拟机平均数的近似下界,并分析了不同参数对排队指标和处于on状态虚拟机数量的影响.
2. School of Information Science and Engineering, Yanshan University, Hebei Qinhuangdao 066004, China;
3. Department of Electronic Engineering, Tsinghua University, Beijing 100084, China;
4. Network Management Center, Xinxiang University, Henan Xinxiang 453003, China
In view of the migration characteristics of virtual machines in cloud service systems, an M/M/m(t) system model with variable number of servers is proposed. A two-dimensional Markovian chain based on the queuing length process of sub-tasks and the number changing process of virtual machines is established. The steady-state distribution of the process and the steady-state performance index of the system are obtained by using matrix geometric theory. Considering the service level agreement, an approximate lower bound of the average number of virtual machines that the system should open is given, and the effects of different parameters on the queuing index and the number of virtual machines in on-state are analyzed.
云服务系统因其可扩展性、灵活性日益受到重视.与传统的网络服务系统不同,该系统具有如下特征:1)具有弹性(Elasticity), 即可以按照业务需求动态调配系统所需的资源;2)资源调度的弹性依靠数量庞大的虚拟机(VM, virtual machine)的迁移来实现[1];3)云服务系统必须按照客户需求提供服务,即在服务水平协议(SLA, service level agreement)前提条件下实现云服务资源的调度.为了保证SLA,云服务系统对服务质量提出了很高的要求.云资源后台调度需要先进的理论和算法支撑才能实现,故研究云服务系统的建模理论成为必然.
如果把虚拟机看做服务台,访问需要视为顾客,则云服务系统可以看做一个排队系统. Khazaei等[2]建立了云服务中心的M/G/m/m+r模型,Chang等[3]借助该模型实现了更加准确的系统性能分析. Cao等[4-5]借助M/M/m模型,从降低电力消耗和收益最大化的角度分别研究了云服务的性能和定价策略.
为了实现服务的弹性,Tian等[6]把云服务系统视作M/G/c模型,利用非线性规划模型,给出了负载的最佳分配策略. Yang等[7]从嵌入马尔可夫链的角度建立排队模型,给出需求等待时间、处理时间及网络延迟的解析结构.在忽略虚拟机迁移速率的前提下,Luo和Li等[8-9]分别提出了阈值控制下的虚拟机调度策略.对于服务台数量庞大的云服务中心,Enver[10]得到了系统稳态分析的封闭形式,并实现了服务台数量等于500的数值模拟. Yin等[11]假设虚拟机可以同步休眠,建立了云服务系统的休假模型,给出了系统休眠率等性能指标.
在实际的云计算系统中,虚拟机的配置和迁移是实现云资源弹性变化的关键所在[12].在调度中预拷贝算法、后拷贝算法和混合拷贝算法是3种常见的虚拟机迁移算法[13-15].系统负载是动态变化的,如果负载较小,虚拟机完成客户响应的需求任务后会释放虚拟机;如果系统负载变大,则负载平衡器将提前感知,发出增加虚拟机的指令.理想的虚拟机调度算法可以实现虚拟机数量的动态变化,这种调控不但可以提高服务质量,还可以帮助云管理中心降低成本,增加收益.
不同于传统阈值控制策略或服务台数确定的排队系统,笔者研究了一个服务台数量可变的M/M/m(t)云服务系统模型,虚拟机的迁移导致服务台数量的变化,而虚拟机的启动与关闭依赖于系统队长和服务台数量的相对变化,而且启动和关闭需要一定的时间.笔者利用Markov分析的方法得到了系统性能指标,在SLA约束下分析了系统需要的处于开启状态最少的虚拟机个数,并分析了不同参数对系统性能的影响.
1 云服务系统描述如图 1所示的云服务系统中,客户的访问需求包含一系列的子任务,这些子任务首先在负载平衡器前的排队室等待处理,假定每一个子任务恰好被某一个虚拟机单独处理.由文献[16-18]知,负载平衡器在云资源调度中起着关键作用,可以感知系统状态等信息,并根据系统资源进行调度.
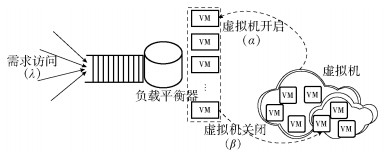
|
图 1 云排队系统示意图 |
假定负载平衡器的服务速率非常大,任务经过负载平衡器的时间相对于被虚拟机处理的时间很小(可以忽略不计),虚拟机处理任务满足先到先服务(FCFS, first come first serve)的机制.负载平衡器可以随时监控到系统中任务数和所有虚拟机的运行状态,虚拟机聚集或迁移可以通过负载平衡器来控制.
如果系统中的任务数量小于系统中正处于开启状态(on)的虚拟机数量,那么新到来的任务将会被负载平衡器直接分配到某一个虚拟机上进行处理;否则,负载平衡器将启动寻找功能,让那些处于关闭状态(off)的虚拟机转入on状态, 在寻找过程结束瞬间,服务台数量增加一个,并立即接受子任务.
在某个虚拟机完成其子任务的时刻,如果系统中的任务数量不大于系统中正处于on状态的虚拟机数量,负载平衡器将启动虚拟机关闭功能,在释放过程完成的瞬间,服务台数量减少一个,该虚拟机将迅速转入off状态.因此,作如下假设:
1) 任务的到达服从Poisson过程,参数为λ;
2) 系统排队室容量较大,排队等待的子任务不会丢弃;
3) 每个虚拟机处理子任务的时间服从参数为μ的指数分布,系统处于on状态的最小虚拟机数量为s(s≥1), 可以利用的所有虚拟机数量记为N;
4) 当虚拟机处于off状态时,负载平衡器会发出开启虚拟机指令瞬间开始,虚拟机经过物理启动、数据拷贝等环节,到进入on状态且可以接受任务的时间是随机的,服从参数为α的指数分布;如果虚拟机正处于闲置状态,那么需要关闭该虚拟机的时间服从参数为β的指数分布.
2 云服务系统模型由图 1可知,云服务系统可以假定为一个服务台数量可变的M/M/m(t)排队系统.由于t时刻处于开启状态的服务台数量m(t)依赖于系统中的子任务数量,因此系统队长过程{L(t), t≥0}不是马尔可夫过程.同时,由于虚拟机服务时间和虚拟机迁移的时间都服从指数分布,故{(L(t), m(t)), t≥0}是连续时间的马氏链,状态空间为Ω={(i, j)|i≥0, s≤j≤N}.其中,s代表系统需要开启的最少虚拟机数量,N代表可开启的虚拟机数量的上界.
将Ω中的状态按照字典序排列,则该马氏链的无穷小生成元矩阵Q有如下形式:
| $ \mathit{\boldsymbol{Q}} = \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{F}}_0}}&{{\mathit{\boldsymbol{E}}_0}}&{}&{}&{}&{}&{}&{}\\ {{\mathit{\boldsymbol{G}}_1}}&{{\mathit{\boldsymbol{F}}_1}}&{{\mathit{\boldsymbol{E}}_1}}&{}&{}&{}&{}&{}\\ {}&{{\mathit{\boldsymbol{G}}_2}}&{{\mathit{\boldsymbol{F}}_2}}&{{\mathit{\boldsymbol{E}}_2}}&{}&{}&{}&{}\\ {}&{}& \cdots & \cdots & \cdots &{}&{}&{}\\ {}&{}&{}&{{\mathit{\boldsymbol{G}}_N}}&{{\mathit{\boldsymbol{F}}_N}}&{{\mathit{\boldsymbol{E}}_N}}&{}&{}\\ {}&{}&{}&{}&{{\mathit{\boldsymbol{G}}_N}}&{{\mathit{\boldsymbol{F}}_N}}&{{\mathit{\boldsymbol{E}}_N}}&{}\\ {}&{}&{}&{}&{}& \cdots & \cdots & \cdots \end{array}} \right) $ | (1) |
其中Ei, Fi, Gi,0≤i≤N都是N-s+1阶矩阵.记I为N-s+1阶单位矩阵,Q的每一个分块矩阵的形式如下:
当0≤i≤s时,Ei=λ I, Gi=iμ I
| $ {\mathit{\boldsymbol{F}}_i} = \left( {\begin{array}{*{20}{c}} { - \lambda - i\mu }&{}&{}&{}&{}\\ \beta &{ - \lambda - i\mu - \beta }&{}&{}&{}\\ {}&{2\beta }&{ - \lambda - i\mu - 2\beta }&{}&{}\\ {}&{}& \ddots & \ddots &{}\\ {}&{}&{}&{\left( {N - s} \right)\beta }&{ - \lambda - i\mu - \left( {N - s} \right)\beta } \end{array}} \right) $ |
当s+1≤i≤N时,
| $ {\mathit{\boldsymbol{E}}_i} = \lambda \mathit{\boldsymbol{I}},{\mathit{\boldsymbol{G}}_k} = \left( {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{G}}_1^{\left( i \right)}}&{\bf{0}}\\ {\bf{0}}&{\mathit{\boldsymbol{G}}_2^{\left( i \right)}} \end{array}} \right),{\mathit{\boldsymbol{F}}_k} = \left( {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{F}}_1^{\left( i \right)}}&{\bf{0}}\\ {\mathit{\boldsymbol{F}}_0^{\left( i \right)}}&{\mathit{\boldsymbol{F}}_2^{\left( i \right)}} \end{array}} \right) $ |
| $ \mathit{\boldsymbol{G}}_1^{\left( i \right)} = \left( {\begin{array}{*{20}{c}} {s\mu }&{}&{}&{}\\ {}&{\left( {s + 1} \right)\mu }&{}&{}\\ {}&{}& \ddots &{}\\ {}&{}&{}&{i\mu } \end{array}} \right),\mathit{\boldsymbol{G}}_2^{\left( i \right)} = \left( {\begin{array}{*{20}{c}} {i\mu }&{}&{}&{}\\ {}&{i\mu }&{}&{}\\ {}&{}& \ddots &{}\\ {}&{}&{}&{i\mu } \end{array}} \right),\mathit{\boldsymbol{F}}_0^i = \left( {\begin{array}{*{20}{c}} 0&0& \cdots &\beta \\ 0&0& \cdots &0\\ \vdots & \vdots & \ddots & \vdots \\ 0&0& \cdots &0 \end{array}} \right) $ |
| $ \mathit{\boldsymbol{F}}_1^i = \left( {\begin{array}{*{20}{c}} { - \lambda - \left( {i - s} \right)\alpha - s\mu }&{\left( {i - s} \right)\alpha }&{}&{}\\ {}&{ - \lambda - \left( {i - s - 1} \right)\alpha - \left( {s + 1} \right)\mu }&{\left( {i - s - 1} \right)\alpha }&{}\\ {}& \ddots & \ddots &{}\\ {}&{}&{ - \lambda - \alpha - \left( {i - 1} \right)\mu }&\alpha \\ {}&{}&{}&{ - \lambda - i\mu } \end{array}} \right) $ |
| $ \mathit{\boldsymbol{F}}_2^i = \left( {\begin{array}{*{20}{c}} { - \lambda - \beta - i\mu }&{}&{}&{}&{}\\ {2\beta }&{ - \lambda - 2\beta - i\mu }&{}&{}&{}\\ {}&{3\beta }&{ - \lambda - 3\beta - i\mu }&{}&{}\\ {}&{}& \ddots & \ddots &{}\\ {}&{}&{}&{\left( {N - i} \right)\beta }&{ - \lambda - \left( {N - i} \right)\beta - i\mu } \end{array}} \right) $ |
这里的G1(i)是i-s+1阶矩阵,G2(k)是N-i阶矩阵,F1(i)是i-s+1阶矩阵,F2(i)是N-i阶矩阵,F0(i)是(N-i)×(i-s+1)矩阵.
3 稳态分析 3.1 稳态条件由无穷小生成元矩阵Q的结构知,马氏链{(L(t)m(t)), t≥0}是拟生灭过程.依据Neuts[19]的矩阵几何理论, 该过程稳态分布存在当且仅当下式成立
| $ \mathit{\boldsymbol{x}}{\mathit{\boldsymbol{G}}_N}\mathit{\boldsymbol{e}} > \mathit{\boldsymbol{x}}{\mathit{\boldsymbol{A}}_N}\mathit{\boldsymbol{e}} $ | (2) |
其中:x是马氏过程{Y(t), t≥0}的稳态概率向量,e是全1列向量,且x满足
| $ \mathit{\boldsymbol{x}}\left( {{\mathit{\boldsymbol{E}}_N} + {\mathit{\boldsymbol{F}}_N} + {\mathit{\boldsymbol{G}}_N}} \right) = 0,\mathit{\boldsymbol{xe}} = 1 $ | (3) |
考虑拟生灭过程{(L(t), m(t)), t≥0},设其稳态分布为π =(π0, π1, π2, …),其中πi=(πi0, πi1, …, πiN),i≥0.
由矩阵几何理论可知, πi(i≥0)具有如下形式:
| $ {\mathit{\boldsymbol{\pi }}_k} = {\mathit{\boldsymbol{\pi }}_0}\prod\limits_{j = 1}^k {{\mathit{\boldsymbol{R}}_j}} ,1 \le k \le N - 1 $ | (4) |
| $ {\mathit{\boldsymbol{\pi }}_k} = {\mathit{\boldsymbol{\pi }}_{N - 1}}{\mathit{\boldsymbol{R}}^{k - N + 1}},k \ge N $ | (5) |
其中R = RN是下面矩阵方程的最小非负解
| $ {\mathit{\boldsymbol{R}}^2}{\mathit{\boldsymbol{G}}_N} + \mathit{\boldsymbol{R}}{\mathit{\boldsymbol{F}}_N} + {\mathit{\boldsymbol{E}}_N} = 0 $ | (6) |
矩阵(6)的解可由下面迭代的方法得到.
步骤1 给定R初值,设R0=0
步骤2 Rn+1=-(EN+ Rn2 GN) FN-1
步骤3 给定小正数ε,若‖ Ri- Ri+1‖ < ε,则迭代停止.
表达式(4)中的Rj, 1≤j≤N-1由下面方程组给出:
| $ {\mathit{\boldsymbol{R}}_j}{\mathit{\boldsymbol{R}}_{j + 1}}{\mathit{\boldsymbol{G}}_{j + 1}} + {\mathit{\boldsymbol{R}}_j}{\mathit{\boldsymbol{F}}_j} + {\mathit{\boldsymbol{E}}_j} = 0 $ | (7) |
由π0(F0+ R1 G1)= 0及归一化条件
| $ {\mathit{\boldsymbol{\pi }}_0}\left( {\mathit{\boldsymbol{I}} + \sum\limits_{k = 1}^{N - 1} {\prod\limits_{j = 1}^k {{\mathit{\boldsymbol{R}}_j}} } + \prod\limits_{j = 1}^{N - 1} {{\mathit{\boldsymbol{R}}_j}} {{(\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{R}})}^{ - 1}}} \right)\mathit{\boldsymbol{e}} = 1 $ | (8) |
得π0及稳态分布π, 其中e是元素全为1的列向量.
3.3 稳态性能指标在云服务系统中,子任务形成的平均系统队长、子任务在系统中的平均逗留时间与客户的体验和满意度直接相关,处于on状态的虚拟机数量是系统能耗的直接影响因素.子任务平均系统队长、子任务的平均逗留时间、平均等待时间及处于on状态的虚拟机平均数如下:
子任务平均系统队长为
| $ L = \sum\limits_{i = 1}^\infty {i{\mathit{\boldsymbol{\pi }}_i}\mathit{\boldsymbol{e}}} $ |
子任务的平均逗留时间为
| $ W = \frac{{\bar L}}{\lambda } = \sum\limits_{i = 1}^\infty {i{\mathit{\boldsymbol{\pi }}_i}\mathit{\boldsymbol{e}}} /\lambda $ |
子任务的平均等待时间为
| $ {W_q} = \sum\limits_{i = 1}^\infty {\frac{{i{\mathit{\boldsymbol{\pi }}_i}\mathit{\boldsymbol{e}}}}{\lambda }} - \frac{1}{\mu } $ |
处于on状态的虚拟机平均数为
| $ S = \sum\limits_{i = 0}^\infty {\sum\limits_{j = m}^N j } {\pi _{ij}} $ |
其中πi由式(4)和式(5)给出.
4 SLA的度量在云服务系统模型中,由于SLA的约束,考虑处于开启状态的最少服务台个数是必要的. SLA的要求有多种方式,譬如对平均传输时延或者等待时间的限定等,实际上这些约束在具体的实践中应用并不方便[17-18].笔者从客户子任务等待时间的概率约束出发,研究系统所需的处于开启的服务台数量.
考虑一个一般的M/M/m排队系统,子任务到达率为λ,每个服务台的服务速率为μ.子任务等待时间是随机的,记为w;子任务的等待时间一个存在一个阈值,记为τ.
由文献[20], 云服务的SLA可以用子任务平均等待时间超过某一阈值τ的概率P{w≥τ}不超过某一约定值θ来刻画,即
| $ P\left\{ {w \ge \tau } \right\} = \frac{{{\rho ^m}}}{{m!\left( {1 - \rho /m} \right)}}{{\rm{e}}^{ - \mu \tau (m - \rho )}}{p_0} \le \theta $ | (9) |
其中:
| $ \frac{{{\rho ^m}}}{{{\rho ^m} + m!(1 - \rho /m)\sum\limits_{j = 0}^{m - 1} {\frac{{{\rho ^j}}}{{j!}}} }}{{\rm{e}}^{ - \mu \tau (m - \rho )}} \le \theta $ | (10) |
记满足式(10)的服务台数量最小值为m*.由于不等式(11)的左端形式较为复杂,实际应用中,可以通过近似的方法求得.
这里考虑的是一种理想情况,即排队系统的服务台全部开启,没有关闭的情况,在顾客到达参数和虚拟机服务参数不变的前提下,由于虚拟机开启还需要一定的时间,这实际上造成了虚拟机服务速率小于理想状态下的服务速率.因此,在云服务系统中,为了满足SLA的要求,实际需要的最小服务台总数s应该不少于m*,即
| $ s \ge {m^ * } $ | (11) |
若取λ=8,τ=0.01,θ=0.02,图 2给出了在单服务台服务速率取不同值时,云服务违约率P{w≥τ}随服务台个数变化时的取值情况.对于给定的服务速率,随着服务台个数m的递增,子任务平均等待时间超出阈值的概率在递减.随着服务速率增大,或者随着ρ的减小,违约的概率在逐步下降,需要的最少的服务台个数m*也在不断越小.可以看到,μ=4时,m*=5;μ=5时,m*=5;μ=6时,m*=4.
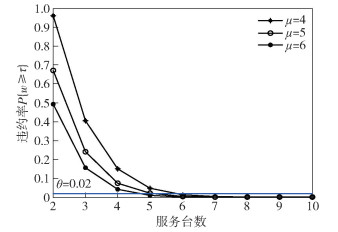
|
图 2 云服务违约率示意图 |
一般而言,在SLA约束下每个虚拟机的服务速率μ相对固定,不妨取μ=4,τ=0.05,α=0.4,θ=0.02,设最大的可以调用的虚拟机数量N=25.
5.1 到达率λ对系统性能的影响随着子任务平均到达速率的变化,需要处于开启状态的虚拟机的最小数量m*、系统稳态队长N,子任务的平均等待时间Wq以及系统处于工作状态的虚拟机的平均数S的变化情况见表 1.
|
|
表 1 到达率λ对系统性能的影响 |
表 1中第2列代表了不同业务强度下,系统需要的最少的虚拟机的数量.可以看到,随着系统子任务平均到达率的增加,按照SLA协议需要的最小的服务台数量m*逐渐变大.系统平均队长有递增趋势,但是由于最小服务台数量的调整,子任务的平均等待时间有一定的波动,系统平均开启的服务台数量也呈单调递增趋势.
5.2 平均开启的服务台数的波动在云计算服务中心,除了要考虑SLA的约束和子任务的排队性能外,虚拟机的能耗是影响系统性能的重要因素,而能耗主要由系统平均开启的服务台数目决定.当μ=4,τ=0.05,α=0.4,θ=0.02,β=0.3,N=25,表 2反映了虚拟机启动速率、平均到达率两个方面因素对系统处于on状态的虚拟机平均数S的影响.
|
|
表 2 虚拟机启动速率α和到达率λ对处于on状态的虚拟机平均数的影响 |
在表 2中,需要处于开启状态的虚拟机的最小数量m*同表 1.随着到达率的递增,处于on状态的虚拟机数量呈递增趋势;虽然,随着虚拟机启动速率α的增加,处于on状态的虚拟机数量S也在增加,但是α对S的影响并不明显.
当μ=4,τ=0.05,α=0.4,θ=0.02,α=0.4,N=25时,表 3反映了虚拟机关闭速率、平均到达率两个方面因素对系统处于on状态的虚拟机平均数S的影响.在表 3中,需要处于开启状态的虚拟机的最小数量m*同表 1.随着到达率的递增,处于on状态的虚拟机数量呈递增趋势;随着虚拟机关闭速率β的增加,处于on状态的虚拟机数量S也在递减,但β对S的影响并不明显.
|
|
表 3 虚拟机关闭速率β和到达率λ对处于on状态的虚拟机平均数的影响 |
云服务系统的建模与性能分析是云资源调度算法设计的基础,一直以来是云计算研究领域的热点.笔者的贡献包括两方面.
1) 用排队的方法建立了虚拟机数量可变的云服务系统的模型,并做了相应的性能分析.不同于一般的服务台数量固定的排队系统,这里充分考虑了虚拟机迁移的特点.虚拟数量的变化由负载平衡器调节,且虚拟机的开启和关闭均需要一定时间.这种假定不但符合虚拟机调用实际环境,而且有助于对调度成本做下一步分析.
2) 在SLA约束下,研究了系统需要开启的最小虚拟机数.借助排队论已有的结论,采用基于某个概率上限的SLA约束,从而给出了系统在满足SLA约束下需要开启的最小虚拟机个数的一个近似求解方法.借助数值模拟,分析不同参数对系统性能指标和系统处于开启状态的虚拟机平均数的影响.
由于模拟软件性能制约,做数值模拟的最大虚拟机数量不够大,未来研究需要对虚拟机的能耗以及虚拟机迁移产生的费用等问题做进一步的分析.
| [1] |
Mostafa N, Abdelhameed I, Hesham A. Optimization of live virtual machine migration in cloud computing:A survey and future directions[J]. Journal of Network and Computer Applications, 2018(110): 1-10. |
| [2] |
Khazaei H, Misic J, Misic V. Performance analysis of cloud computing centers using M/G/m/m+r queuing systems[J]. IEEE Transactions on Parallel and Distributed Systems, 2012, 23(5): 936-943. DOI:10.1109/TPDS.2011.199 |
| [3] |
Chang X, Wang B. Modeling active virtual machines on IaaS clouds using an M/G/m/m+K queue[J]. IEEE Transactions on Services Computing, 2016, 9(3): 408-420. DOI:10.1109/TSC.2014.2376563 |
| [4] |
Cao J, Kai H, Li K, et al. Optimal multiserver configuration for profit maximization in cloud computing[J]. IEEE Transactions on Parallel & Distributed Systems, 2013, 24(6): 1087-1096. |
| [5] |
Chen W, Cao J, Wan Y. QoS-Aware virtual machine scheduling for video streaming services in multi-Cloud[J]. Tsinghua Science and Technology, Special Section on Cloud Computing, 2013, 18(3): 308-317. |
| [6] |
Tian Y, Lin C, Li K. Managing performance and power consumption tradeoff for multiple heterogeneous servers in cloud computing[J]. Cloud coputation, 2014(17): 845-955. |
| [7] |
Yang Z, Liu W, Xu D. Study of cloud service queuing model based on imbedding Markov chain perspective[J]. Cluster Computing, 2017(6): 1-8. |
| [8] |
Zuo L, Shu L, Dong S, et al. Dynamically weighted load evaluation method based on self-adaptive threshold in cloud computing[J]. Mobile Networks and Applications, 2017, 22(1): 4-8. |
| [9] |
Li Z. An adaptive overload threshold selection process using Markov decision processes of virtual machine in cloud data center[J/OL]. Cluster Computing, 2018. https: //doi.org/10.1007/s10586-018-2408-4.
|
| [10] |
Enver E. Performability analysis of cloud computing centers with large numbers of servers[J]. Journal of Supercomputing, 2017(73): 1-27. |
| [11] |
Yin C, Jin S. An energy-saving strategy based on multi-server vacation queuing theory in cloud data center[J/OL]. The Journal of Supercomputing, 2018. https: //doi.org/10.1007/s11227-018-2513-4.
|
| [12] |
LoridoBotran T, MiguelAlonso J, Lozano J. A review of auto-scaling techniques for elastic applications in cloud environments[J]. Journal of Grid Computing, DOI10.1007/s10723-014-9314-7.
|
| [13] |
马飞, 刘峰, 李竹伊. 云计算环境下虚拟机快速实时迁移方法[J]. 北京邮电大学学报, 2012, 35(01): 103-106. Ma F, Liu F, Li Z Y. Fast live migration method of virtual machine in cloud computing environment[J]. Journal of Beijing University of Posts and Telecommunications, 2012, 35(01): 103-106. DOI:10.3969/j.issn.1007-5321.2012.01.024 |
| [14] |
吴小东, 韩建军. 云数据中心基于阈值的虚拟机迁移节能调度算法[J]. 华中科技大学学报(自然科学版), 2018, 46(09): 30-34. Wu X D, Han J J. Threshold-based energy efficient VM scheduling in cloud datacenters[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2018, 46(09): 30-34. |
| [15] |
姜栋瀚, 林海涛. 云计算环境下的资源分配关键技术研究综述[J]. 中国电子科学研究院学报, 2018, 13(03): 308-314. Jiang D H, Lin H T. A summary of key techniques research on resource allocation in cloud computing environment[J]. Journal of China Academy of Elecronics and Information Technology, 2018, 13(3): 308-314. DOI:10.3969/j.issn.1673-5692.2018.03.013 |
| [16] |
Salah K, Elbadawi K, Boutaba R. An analytical model for estimating cloud resources of elastic services[J]. Journal of Netw System Management, 2016, 24(2): 285-308. DOI:10.1007/s10922-015-9352-x |
| [17] |
Green L V, Soares J, Giglio J F, Green R A. Using queueing theory to increase the effectiveness of emergency department provider staffing[J]. Academic Emergency Medicine, 2006, 13(1): 61-68. |
| [18] |
Izady N, Worthington D J. Setting staffing requirements for time-dependent queueing networks:the case of accident and emergency department[J]. European Journal of Operational Research, 2012(219): 531-540. |
| [19] |
Neuts F. Structured stochastic matrices of M/G/1 type and their applications[M]. New York: Marcel Dekker, 1989: 205-206.
|
| [20] |
唐应辉, 唐小我. 排队论:基础与分析技术[M]. 北京: 科学出版社, 2006: 50-53.
|


