提出了自适应加窗小波变换方法,实现了心电特征波形精准定位.依据Q波和S波变化趋势识别出心电波有效起始点和终止点;结合差分阈值法检测QRS起始点,实现了心电特征波段的信息识别.研究结果表明,采用提出的定位识别方法,能对异常和亚健康心电波形进行有效识别,提高对QRS波群、特征P波和T波的识别度,对心电信息的提取和异常性心绞痛、心肌缺血、不稳定型心绞痛等心电异常诊断具有重要意义.
An adaptive windowed wavelet transform method was proposed to make precision positioning of the electrocardiography feature waveforms. The effective starting and ending points of electrocardiography wave were identified according to the trend of Q wave and S wave. The information recognition of the electrocardiography characteristic band was realized by combining the differential threshold method to detect the QRS starting. It is shown that the proposed method can effectively identify abnormal and sub-healthy electrocardiography waveforms and improve the recognition of QRS wave group, P wave and T wave for extration of electrocardiography information and diagnosis of abnormal electrocardiography such as abnomal angina pectoris, myocardial ischemia and unstable angina pectoris.
心电监测是目前反映心电活动的主要技术, 心电波形常作为诊断心脏异常、心脏疾病的参考依据.临床上对心电波形的识别认知多具有主观性, 且人工工作量大, 识别诊断工作较为繁琐.针对此问题, 自动识别心电特征, 以实现自动识别动态心电图具有重要的理论意义和实际应用价值.
近些年, 心电波形自动识别技术迅猛发展, 分析方法层出不穷, 有时域、频域、小波和功率谱特征等方法, 这些方法主要以QRS波群检测为出发点[1-3].目前有很多QRS波群检测算法, 如差分阈值检测方法、模板匹配法、神经网络算法、希尔伯特变换法和小波变换法[4-8].
差分阈值法的检测准确性依赖于信号预处理的好坏, 对预处理的依赖较高; 模板匹配法直观易懂, 但是作为模板的心电波形需要具有高度代表性, 而在临床中心电波形具有很大差异性, 这导致模板匹配法在实际应用中不具有可靠性; 神经网络算法在保证训练数据量的基础上对各类波形具有高检测度, 但是该算法局限于非线性预测; 希尔伯特变换法能获取形态信息, 但是易受噪声影响.小波变换具有较好的时频局域化和多分辨率分析特性, 研究者对其在图像融合、处理, 雷达, 机械等方面的应用进行了较为深入的研究.在医学领域, 小波变换在心电信号去噪方面有较为成熟的应用, 但在心电识别中的应用处于起步阶段, 尤其在异常心电识别中由于识别效果不佳使用更少.随着识别方法不断改进, 识别精确度不断提高, 识别分析从QRS波群特征提取转向P、T和ST段特征参数提取, 并取得了一些成果[9].
异常心电波形具有特异性和不规则性, 传统方法对异常波形的识别存在较大误差[10-13].为了提高异常心电波形识别精准度, 笔者基于二样条小波变换提出了自适应加窗小波变换, 最后结合差分阈值方法有效识别异常心电波形, 提取心电特征, 提高了QRS波群、特征P波和T波的识别度, 对典型常见心脏类疾病诊断和预测有重要指导性作用.
1 异常心电信号特征识别理论 1.1 心电信号识别分析心电波形的识别特征参数包括幅值、持续时间和波形形态.幅值参数包括R波、P波、Q波、S波、T波的幅值和ST段幅值偏移量; 持续时间参数包括RS波群时间宽度、P波时间宽度、RR时间宽度、P-R时间宽度、QT时间宽度和ST时间宽度; 波形形态即每个观察周期内心拍与各波段的波形.相比于其他波段, QRS波形特征更为明显, 尤其是R波具有高幅值、高斜率的特点, 所以想要心电波提取群的特征, 先实现QRS波群检测(心电波群的特征提取起始于QRS波群检测), 而QRS波群检测从定位R波开始, 识别心电信号中的R波形态特征.如果信号或信号的某阶导数在一个点产生突变, 则这个点是信号的一个奇异点.所以, QRS波群中R波的检测可以归结为信号奇异点的检测.笔者提出的自适应加窗小波变换能在小波变换的基础上增加自适应时间窗, 准确识别心电特征的R波奇异点.
1.2 心电信号小波变换中的奇异点心电信号的奇异性通常在李氏指数(Lipschitz)处有所变化, 随着尺度的逼近, 信号奇异点将越来越接近小波变换的模极大值.基于连续小波变换和多种策略QRS波群检测的方法, 奇异点的李氏指数将决定着信号衰减的情况, 因此李氏指数对心电时域信号x(t)的奇异性有较好的描述作用[14].李氏指数的定义如下所述.
|Wx(a, b)|为心电信号x(t)小波, 令0≤α < 1, 如果存在一个常数C, 使∀t∈R, 均有
| $ \left| {x\left( t \right) - x\left( {{t_0}} \right)} \right| \le C{\left| {t - {t_0}} \right|^\alpha } $ | (1) |
成立, α为非整数, 且存在常数A, 使得
| $ \begin{array}{*{20}{c}} {\left| {{W_x}(a,b)} \right| \le A{a^{\alpha + 0.5}}\left( {1 + {{\left| {\frac{{t - {t_0}}}{a}} \right|}^\alpha }} \right)}\\ {\left( {\forall a \in {\mathit{\boldsymbol{{\rm{R}}}}^ + },t \in \mathit{\boldsymbol{{\rm{R}}}}} \right)} \end{array} $ | (2) |
则称心电信号x(t)在t0处的李氏指数为α.其中, a表示心电信号中的任意一个采样点位置.心电信号x(t)在t0时间点的导数阶次越高, 李氏指数越大, 心电信号在t0处越平滑.
若小波函数φ(t)的支撑范围为[-C, C], 则小波系φa, b(t)的支撑范围是[t-Ca, t+Ca].使t0包含在φa, b(t)范围内的所有点的集合就是心电信号奇异点t0的影响范围:
| $ \left| {t - {t_0}} \right| \le Ca $ | (3) |
在影响范围内, 心电信号x(t)小波变换满足
| $ \left| {{W_x}(a,b)} \right| \le A{a^{\alpha + 0.5}} $ | (4) |
固定横坐标a0, 若点(a0, t0)是函数|Wx(a, t)|的局部极值, 该点满足
| $ {\rm{lb}}\left| {{W_x}(a,t)} \right| \le {\rm{lb}}A + j(\alpha + 0.5) $ | (5) |
由式(5)可以得到结论:若信号在t0处的李氏指数α>0, 随着变换尺度j的增加, 小波变换的模极大值会增加; 当α≤0时, 模极大值减小或不发生变化.所以在小波高尺度域内使用小波变换很容易找到模极大值点.在心电波形中, 幅度值高, 波形变化快的QRS波群存在多个奇异点.根据极值点与导函数的关系, 若采用一阶导函数, 小波系数Wx(1)(a, t)中等于0的点与信号x(t)中的极值点相对应, Wx(1)(a, t)的极值点与信号x(t)中的转折点相对应; 二阶导数Wx(2)(a, t)中等于0的点与信号x(t)中的转折点相对应, Wx(2)(a, t)的极值点与信号x(t)中的极值点相对应.综上分析, 通过检测Wx(2)(a, t)中的零点或者极值点, 可以实现检测心电波形信号QRS波群的极值点.
1.3 构建分层滤波器在实际检测中, 要想使用小波函数较准确地定位信号中的奇异点, 不仅需要函数有较好的定位特性, 还需要有较高的分析精度.样条小波的优点不胜枚举, 其不仅具有较好的对称性, 还具有非紧致正交性[15].下面采用多抽样滤波器组技术对信号进行分解.
由于异常心电信号基线漂移, 工频干扰和肌电干扰频率覆盖在3个频段, 所以采用双正交二次B样条小波[16]对心电信号进行分解.通过构造正交条样滤波器把心电信号按照模极大值点的频率分成4层, 选用低通滤波器和高通滤波器实现频率分层.滤波器系统函数如下所述.
令H0(z)与H1(z)分别是信号x(t)进行分解的低通、高通滤波器, G0(z)和G1(z)是对应的重构滤波器[17].由滤波器组的理想重构条件可得
| $ \begin{array}{*{20}{c}} {Y(z) = \left[ {{H_0}(z){G_0}(z) + {H_1}(z){G_1}(z)} \right]\frac{{Z(z)}}{2} + }\\ {\left[ {{H_0}(z){G_0}(z) + {H_1}(z){G_1}(z)} \right]\frac{{Z( - z)}}{2}} \end{array} $ | (6) |
要使输出函数满足
| $ y(n) = x(n - k) $ | (7) |
则对应的z变换为
| $ Y(z) = X(z){Z^{ - k}} $ | (8) |
消除X(z)引起的失真可得
| $ {H_0}( - z){G_0}(z) + {H_1}( - z){G_1}(z) = 0 $ | (9) |
使Y(z)成为X(z)的纯迟延, 有
| $ {H_0}(z){G_0}(z) + {H_1}(z){G_1}(z) = mz - k $ | (10) |
令
| $ {P_0}(z) = {H_0}(z){G_0}(z) $ | (11) |
则
| $ {H_0}(z){G_0}(z) + {H_0}( - z){G_0}(z) = mz - k $ | (12) |
| $ {P_0}(z) = {\left( {1 + {z^{ - 1}}} \right)^{2p}}Q(z) $ | (13) |
k应为奇数, 故P0(z)中只有一个奇次项.其中, p为任选整数, Q(z)为(2p-2)次的多项式.取p=2, 则P0(z)是(4p-2)=6次的多项式, 所以取k=3, 有
| $ {P_0}(z) = {\left( {1 + {z^{ - 1}}} \right)^4}\left( { - 1 + 4{z^{ - 1}} - {z^{ - 2}}} \right)/16 $ | (14) |
| $ {H_1}(z) = \left( { - 1 - 3{z^{ - 1}} + 3{z^2} + {z^{ - 3}}} \right)/4 $ | (15) |
| $ {H_1}(z) = \left( { - 1 + 3{z^{ - 1}} - 3{z^2} + {z^{ - 3}}} \right)/4 $ | (16) |
由式(6)~式(16)可以确定高通滤波器和低通滤波器的系数分别为
| $ {g_0} = - \frac{1}{4},\;{g_1} = - \frac{3}{4},\;{g_2} = \frac{3}{4},\;{g_3} = \frac{1}{4} $ |
| $ {h_0} = \frac{1}{4},{h_1} = \frac{3}{4},{g_2} = \frac{3}{4},{g_3} = \frac{1}{4} $ |
R波在波群中具有高频率、高幅度的特性, 且4分层小波变换检测出R波具有极值点偏移的情况, 而且容易受到干扰.下面在小波变换、频率分层后在相应层添加自适应窗, 能校正识别错误的R波, 有效改善极值点的漂移问题[18-20], 具体流程如图 1所示, 异常心电识别样例如图 2所示.

|
图 1 自适应加窗小波变换R波检测流程 |
|
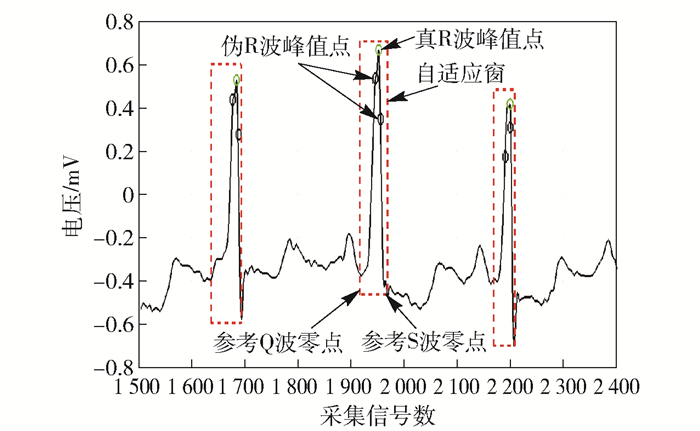
图 2 对心室颤动心电采用自适应加窗小波变换R波检测 |
图 1中, 小波变换将心电信号按频率分解成4层, 分别用细节系数表示为cd1、cd2、cd3、cd4, 从1层到4层细节系数对应的频率依次递增.由于R波具有高频、高幅度特性, 在第4尺度上能够搜寻到细节系数的模极值, 所以依据经验阈值能够筛选出正负模极大值对, 确定过零点的位置.
异常心电波形具有周期性和规则性特征, 在指定频率尺度上使用自适应窗搜索, 即在一系列极值中选取最大值, 保证R波识别的精确性. Q波和S波的模极值对主要存在于第2尺度上, 对细节系数cd2分别求R波波峰零点左边和右边的第1个零点可以得到Q波和S波的零点, 取Q波的零点作为时间域自适应窗的左边界, S波的零点作为窗的右边界, 则有R波窗函数Rwindows(i)=S(i)-Q(i), 其中i为波群位置的索引值, 在窗内搜索到的R波峰值点即是识别校正后的R波波峰.
如图 2所示, 针对心室颤动心电波形使用自适应加窗小波变换对R波进行检测识别.在第2尺度上搜寻到参考的Q波与R波零点, 将这些零点分别作为自适应窗的左边界和右边界.在一个自适应窗内存在多个R波过零点, 这些过零点在心电图中反映为多个伪R波峰值点, 在窗函数中搜索出过零点的极值点即为真R波峰值点.
2 异常心电识别度仿真分析和验证依据所提出的自适应加窗小波变换法在MATLAB环境中进行仿真实验.实验中进行仿真验证的数据来自于MIT-BIH标准心电库.文中展示出的心电波形为常见异常波形, 如预激综合征发生房颤产生的心室融合心跳、窦性停搏引起的长周期低幅度心跳、不稳定型心绞痛伴随的多极值点Q波与S波等.使用MIT-BIH标准心电库中的异常心电数据对波群R波的识别度, 波群起始、终止点识别率和异常心电识别效果进行了仿真和性能分析, 对波形检测中出现的多极值点Q波和S波以及在边界特征识别过程中出现的多极值点边界情况进行了仿真和性能验证.
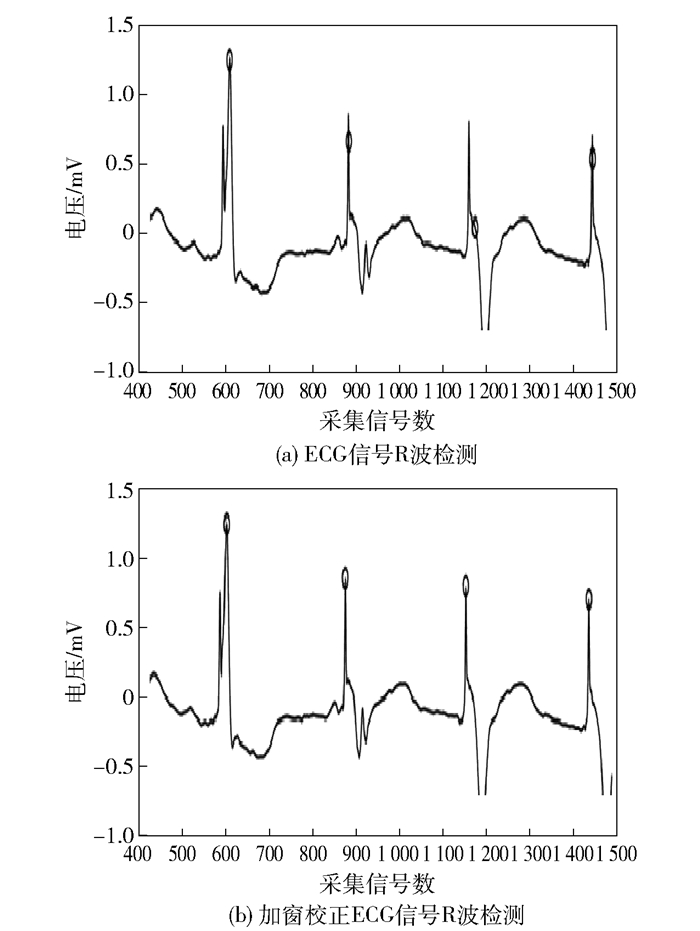
2.1 定位波群中的R波MIT-BIH心电数据库中记录了使用holter采集的各类异常心电患者信息.排除人为因素, 随机选取心电数据库中的8个子数据库对自适应加窗小波变换与普通小波变换R波识别度进行对比实验. 图 3所示为随机采集的104号子心电库中的起搏融合心跳心电信息对R波识别效果的比较分析.从图 3中可看出, 采用小波变换特征识别方法得到的R波定位点会存在偏移, 甚至还可能出现R波定位错误的情况; 若采用自适应加窗小波变换对R波进行检测, 则能从形似极值点的众多点中搜索出一个最大值, 这样能保证R波定位的精确性, 对后续的特征提取意义重大.
|
图 3 心室融合心跳自适应加窗小波变换R波检测对比 |
对采集的8个心电子数据库做识别度比较实验, 识别度比较结果如表 1所示.从表 1中可以看出, 对编号100、101、102、103子数据库使用小波变换进行特征识别, 得到的识别度比较高, 使用自适应加窗小波变换能继续保持比较高的波群识别度, 对心电波形定位QRS波群具有良好的指导作用. 表 1中编号105和108子数据库由于存储的心电信息本身存在比较大的误差和杂乱波形, 相对于小波变换识别检测方法, 采用所提出的自适应加窗小波变换方法识别度有了较大的提高, 分别由61.747%和73.944%提高到87.175%和93.363%.
|
|
表 1 R波识别度改进前后效果对比 |
心电波群起始点作为心电波形的边界特征是心电波形的重要属性, 在实际的识别工作中, 心电波群的边界特征识别以识别波形特征点为基础展开.在心电特征识别中, 波群起始和终止点常作为诊断的重要标准, 所以识别波群的起始和终止点特征意义很大.在识别波群持续时间中, Q波起始点和S波终止点常作为波群识别的起始和终止参考点.
Q波以及S波为高频低幅波, 在分布上处于较低尺度.对极大值域对比分析, 确定在细节系数cd2上, 可以进行Q波和S波检测. Q波、S波和R波紧密相连, 其中Q波的波峰是R波的起点而S波的波峰则是R波的终点, 由Q波和S波所生成的模极值对与R波生成的模极值对紧密相关. Q波和S波存在于心电波形奇异点覆盖范围内, 使用波群奇异点检测, 借助模极值对之间的过零点进行Q波和S波检测, 对于大幅值的R波, 其所生成的模极值对几乎不会受噪声干扰, 但实验中发现Q波所生成的模极值对的首波和S波所生成的模极值对的尾波往往检测不理想, 笔者采用对QRS波群自适应加窗小波变换方法, 在cd4层R波所生成的模极值对左右两侧搜索过零点, 分别对Q波起点和S波终点进行定位.
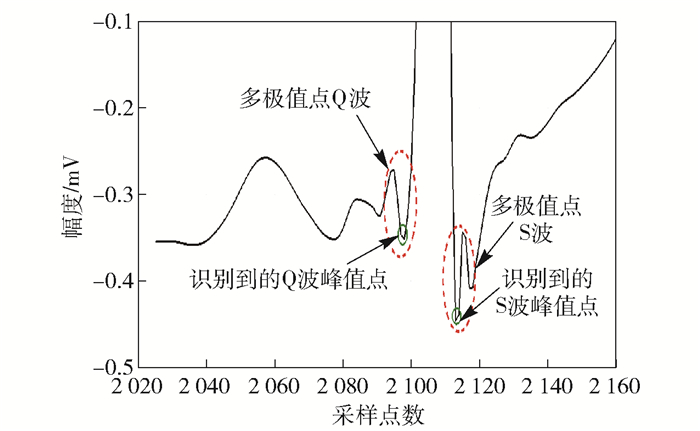
从图 4中可以看到, 在实际检测心电过程中, 由于心跳抖动或者不规则心跳扰动较大会导致Q波和S波出现较多极值点.由于心电波形中Q波和S波既是波形的2个极值点也是峰值点, 在已经得到R波峰值点的情况下, 使用自适应加窗小波变换, 对Q波和S波有很好的识别效果.
|
图 4 多极值点Q波和S波信号现象图解 |
所提出的自适应加窗小波变换方法在第2层小波系数中搜索Q波和S波正负极值对, 获取Q波和S波的零点Q(i)、S(i), 将Q波和S波的零点作为矩形窗的中轴, 即Qaxis(i)=Q(i), Saxis(i)=S(i), R波零点和Q波零点的间距作为Q波校正半矩形窗宽度, 即Q波的校正矩形窗函数Qwindows(i)=2QRinterval(i), S波的校正矩形窗函数Swindows(i)=2SRinterval(i), 其中i为波群的索引值, SRinterval为S波零点和R波零点的间距, QRinterval为Q波零点和R波零点的间距, 识别结果如图 4所示.
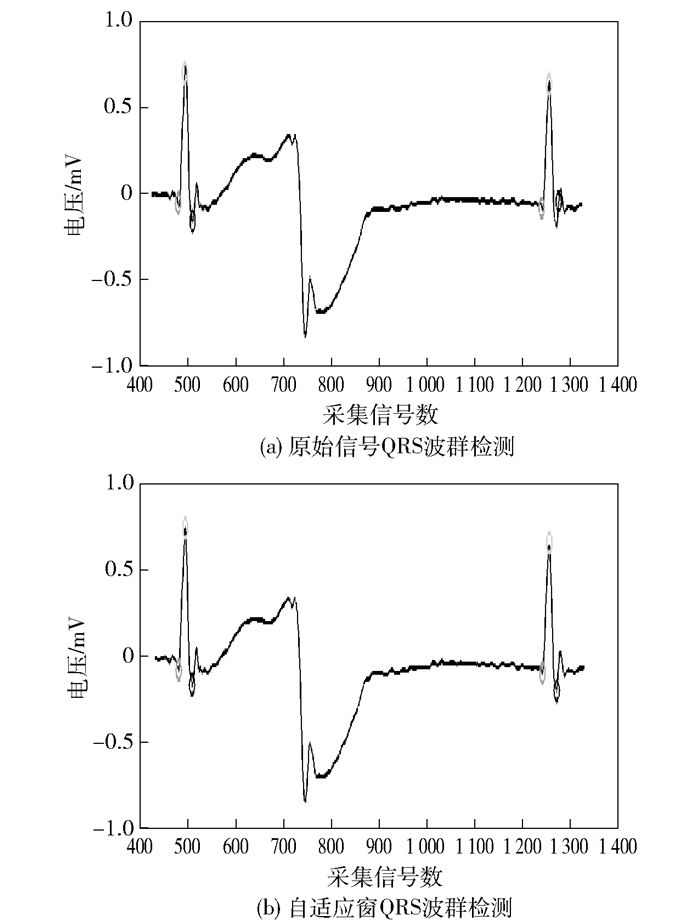
从图 5中可以观察到使用自适应加窗小波变换添加自适应窗后波群特征点检验的优化结果.自适应加窗小波变换的检验方式对于常规波形具有比较稳定的检验结果, 对于Q波和S波存在较多极值点的特征波, 则在一簇极值点中选取出最值作为Q波与S波的特征点, 该方法能保证极值点的唯一性和准确性.
|
图 5 QRS波群检测改进效果对比 |
表 2是对随机选取的异常心电数据库中12个子库中的典型心电波形进行性能验证的结果. 表 2中显示, 合计140个QRS波群检验中正确率高达95%, 误检和漏检分别占2.86%和2.14%, 符合波形检验正确率的要求.实验结果表明, 自适应加窗的小波变换方法对于异常QRS波群的识别效果良好.
|
|
表 2 心电数据库中QRS波群检测结果 |
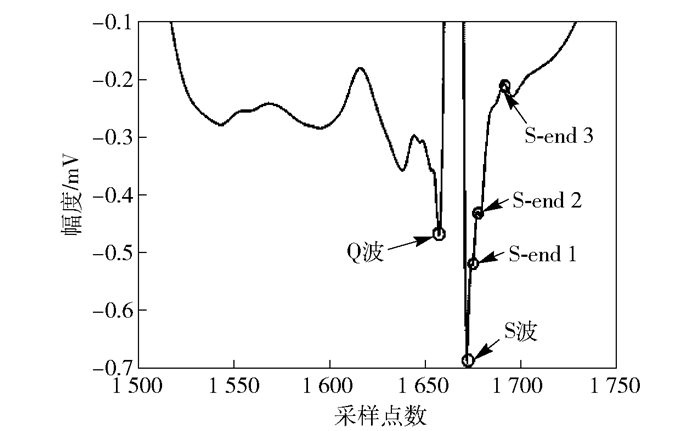
QRS波群起始和终止点信息常作为临床上突发心脏异常(如休克、心绞痛等)的诊断标准, QRS起始点有效性识别具有重要的意义.波群中Q波的起点与QRS波群的起点是同一个位置, S波的终点与QRS波群的终点是同一个位置.但是与QRS波群的其他部分相比, QRS波群的起点和终点形态具有多样性.起始点可能是特征波附近的第1个过零点, 也可能是信号前端或后端的某个过零点. 图 6中呈现的是S波边界识别过程中存在多个极值点的情况.在识别QRS波边界时, 由于存在细小的起伏极值点, 依靠获取最近零点的方式可能获得边界点S-end1或者S-end2, 而波群的边界点在S-end3处, 这样获取边界极值点的方式在某些特殊波形中会造成比较大的误差.由于QRS波群是一群具有固有变化趋势的周期波形, 笔者提出了依据Q波和S波变化趋势识别出有效的起始点和终止点的方法.
|
图 6 多极值点S波边界识别 |
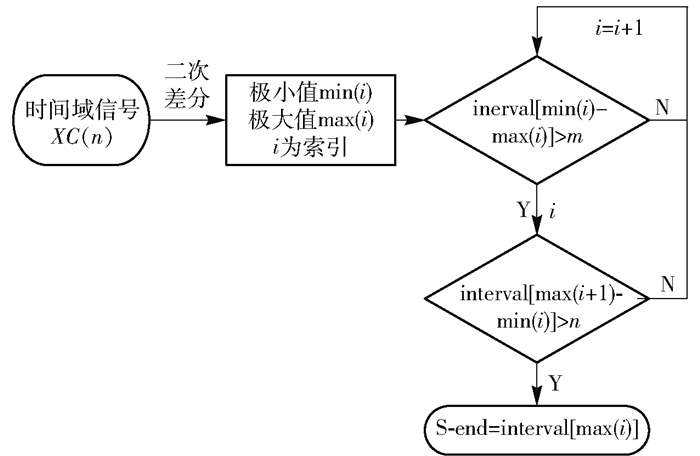
统计心电QRS波形特征可知, Q波起点和S波终点主要位于极大值点和极小值点交界处, 且极值点之间的间隔比较大.基于QRS波群的该种变化特性, 笔者将差分阈值算法运用在检测QRS起始点中.为了描述方便, 以确定S波终止点为例(Q波起始点识别同理), 算法实现流程如图 7所示.
|
图 7 差分阈值识别S波终点流程 |
二次差分处理信号得到差分函数满足
| $ X{C^2}\left( n \right) = \left\{ \begin{array}{l} - 1,\;\;\;\;极大值点\\ 0,\;\;\;\;\;\;极值间隔点\\ 1,\;\;\;\;\;\;\;极小值点 \end{array} \right. $ | (17) |
根据相邻极小值点和极大值点之间的间隔大于阈值m和下一个极大值点和极小值点之间的间隔大于阈值n判断极大值点是否是S波的边界.
针对MIT-BIH心电库中存在Q波和S波边界值多极值点的问题, 对比分析差分阈值和经验的方法对边界值的识别准确率.规定识别的边界值与实际边界值相差5个采样间隔, 即可认为边界识别产生误差.如表 3所示, 在12个子心电库中各取50个心拍, 使用经验识别的方式识别异常心电的边界值存在随机性, 识别的准确率不高, 使用差分阈值的方式能在众多的极值点中找到边界收敛的趋势进而找到边界值. 205、219、220、222和228这5个子心电库使用了差分阈值的方法, 准确率有较大的提升.实验证明, 使用差分阈值能准确识别波群边界值, 对心电识别有着良好的指导作用.
|
|
表 3 心电库中经验和差分阈值波群边界识别准确率对比 |
针对异常心电波形特征点和波群边界值的识别, 采用自适应加窗小波变换的方法有效解决了心电波形中Q波、R波和S波存在抖动的影响, 提高了特征点识别的准确性.基于波群边界值具有丰富的心电波形信息, 采用差分阈值的方法确定波群边界值, 提升了边界值识别的准确率.研究结果对波群精准定位和异常心电信息识别有重要的理论意义和实际应用价值.
| [1] |
Wang L, Zheng C X, Ye J L, et al. A very efficient real-time QRS detection method[J]. Beijing Biomedical Engineering, 1998(4): 217-222. |
| [2] |
Cheng X M, Lin J S, Zhang Z G. An improved template matching method for high resolution ECG[J]. Chinese Journal of Biomedical Engineering, 1999, 18(1): 89-96. |
| [3] |
Chen Y Q, Li G, Ye W Y, et al. An improved algorithm of adaptive coherent model in the application of electrocardiograph[J]. Signal Processing, 2002, 18(3): 244-248. |
| [4] |
马玉润. ECG预处理与QRS波群检测技术研究[D].兰州: 兰州大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10730-1013238627.htm
|
| [5] |
Liu Z D, Chen J, Tang M F. Pulse transit time detection based on waveform time domain feature and dynamic difference threshold[J]. Journal of Biomedical Engineering, 2017, 34(3): 329-334. |
| [6] |
Yan H L, An Y, Wang H F, et al. Feature extraction of ECG hearbeats based on convolutional neural networks[J]. Computer Engineering and Design, 2017, 38(4): 1024-1028. |
| [7] |
Zhang J L, Zheng X. Stationary wavelet transform and new threshold function used in ECG signal denoising[J]. Journal of Beijing University of Posts and Telecommunications, 2017, 40(1): 28-31. |
| [8] |
Kher R, Vala D, Pawar T, et al. Implementation of derivative based QRS complex detection methods[C]//3rd International Conference on Biomedical Engineering and Informatics. Yantai: [s. n.], 2010: 927-931.
|
| [9] |
Dong S, Xu F, Lingwood B, et al. R-wave detection: a comparative analysis of four methods using newborn piglet ECG[C]//International Conference on Information Sciences Signal Processing & Their Applications. Kuala Lumpur: [s. n.], 2010: 320-323.
|
| [10] |
Zhang Q L, Su S M, Wang M. QRS feature extration algorithm based on wavelet transform[J]. Journal of Zhengzhou University, 2017, 49(4): 100-103. |
| [11] |
姚成.心电信号智能分析关键技术研究[D].长春: 吉林大学, 2012.
|
| [12] |
Yochum M, Renaud C, Jacquir S. Automatic detection of P, QRS and T patterns in 12 leaders ECG signal based on CWT[J]. Biomedical signal processing and control, 2016(25): 46-52. |
| [13] |
Madeiro J P, Cortez P C, Marques J A, et al. An innovative approach of QRS segmentation based on first-derivative, Hilbert and wavelet transforms[J]. Medical Engineering & Physics, 2012, 34(9): 1236-1246. |
| [14] |
Wang Z X, Zhang S J, Zeng X P. Shape recognition algorithm for ST-segment of ECG signal[J]. Journal of Computer Applications, 2011, 31(10): 2811-2810. |
| [15] |
Gao Z, Kong F, Zhang X. Accurate and rapid QRS detection for intelligent ECG monitor[C]//Third International Conference on Measuring Technology and Mechatronics Automation.[S. l.]: IEEE Computer Society, 2011: 298-301.
|
| [16] |
Dai J X, Li Z X, Song H X. The analysis and application of signal Lipschitz exponent based on wavelet[J]. Journal of Nanjing University of Posts ant Telecommunications (Natural Science), 2008, 28(6): 69-73, 82. |
| [17] |
Ma A P, Liu L. Research on fault signal detection of transmission line based on wavelet theory[J]. Sichuan Electric Power Technology, 2010, 30(5): 356-361. |
| [18] |
赵毅.基于小波分析和神经网络的异常心电信号分类研究[D].太原: 太原理工大学, 2015.
|
| [19] |
Su L M, Dai Q J, Wang J. R waveform calibration and QRS waveform detection of B-splines-based biorthbogonal wavelets[J]. Journal of Clinical Rehabilitative Tissue Engineering Research, 2009, 13(9): 1657-1660. |
| [20] |
马宪.远程动态心电信号的信息提取与认知[D].北京: 北京邮电大学, 2013. http://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CMFD&filename=1013244305.nh
|


