2. 重庆大学 计算机学院, 重庆 400044
直接设计对于图的加密算法比较困难,为此,提出了2种解决方案.一是借鉴二维易辛模型简单高效和局部化的优点;二是将图的加密问题转换成较简单问题的组合.通过改进基本的易辛模型设计了用于一维数据、二维数据、树结构的加密算法,最终实现了图的加密.分析和实验结果表明,该方法可以实现图加密所要求的可逆性、多样性、高效性、随机性和扩散性等.
2. College of Computer Science, Chongqing University, Chongqing 400044, China
As graph structure is widely applied in science and engineering, it has good practical value to design graph encryption algorithm. Since it is difficult to directly design an encryption algorithm for a graph, two methods are introduced to solve this problem. First, the advantages of 2D Ising model, such as simplicity and locality, are introduced to the design of encryption. Second, the problem of graph encryption is transferred to several simple problems. Encryption algorithms for one-dimension data, two-dimension data, tree-structure are proposed based on the improved Ising model. Finally, the graph encryption algorithm is implemented. Analysis and simulation demonstrate that the proposed method can fulfill basic requirements of graph encryption, including reversibility, adaptability, efficiency, randomness and diffusion.
图是一种由顶点和边组成的数学结构,在物理、化学、生物学、工程[1]、计算机科学[2-3]和社会科学[4-5]等学科的研究中有着广泛的应用.此外,大量的科研和工程数据也以图的形式保存.若这些科研或工程数据涉及机密信息,则在通信和存储前应先加密.传统的加密算法将所有数据都看作一维结构,加密将破坏图的结构.借助易辛模型(Ising model)提出了一种图加密算法.该算法充分考虑图本身的特点,在对图结构和图节点数据加密之后,可以保留图数据的组织结构,具有很好的应用价值.
1 易辛模型易辛模型是Lenz提出的一个统计力学模型[6],用于研究晶体的磁性.它由许多格点构成,每个格点处于向上或向下的自旋状态.每个格点与相邻的上、下、左、右4个格点存在相互作用.格点状态的改变受到式(1)所示的能量公式影响:
| $ H(\sigma ) = - \sum\limits_{ < i, j > } {{J_{i, j}}} {\sigma _i}{\sigma _j} - \mu \sum\limits_j {{h_j}} {\sigma _j} $ | (1) |
其中:参数Ji, j表示格点之间的相互作用,σ代表一个格点的自旋,hj代表模型的外部条件.当晶体处于绝对零度时,所有格点的状态统一向上或统一向下,系统就表现出铁磁性.升高到一定温度时,某些格点的状态受到扰动,从而使系统处于无序状态.
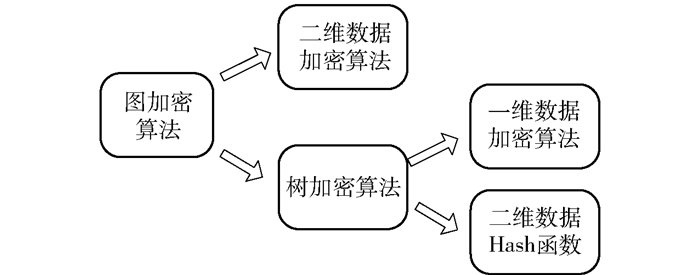
2 基于易辛模型的图加密算法直接设计图加密算法是一个比较复杂的问题.图加密算法可转换为对树结构的加密问题,并进一步分解为更简单的子问题. 图 1显示了图加密算法与其他算法之间的依赖关系.
|
图 1 图加密算法与其它算法的依赖关系 |
一维数据中,各元素排成一行,每个元素包含1 bit信息.一维数据的拓扑结构与一维易辛模型在结构上是相同的,但需要解决可逆的问题.
把元素按序号分成2类,序号为奇数的元素称为奇格;否则称为偶格.很明显,在一维结构中,与奇格相邻的元素均为偶格,反之亦然.这样,可以设计一种可逆变换,依次对奇格和偶格进行并行处理.具体过程在算法D1Enc中描述.
算法名称:D1Enc
输入:
d:待加密的一维数据
k:密钥
输出:
d:加密后的一维数据
过程:
n=d. size //一维数据包含的比特个数
FOR r=1: n //加密轮数等于n
//对全体奇格并行加密.
假设di是一个奇格,其加密由式(2)表示.
| $ {d_i} = {d_i} \oplus {S_1}\left( {x, y, {k_i}} \right) $ | (2) |
//对全体偶格并行加密.
假设dj是一个偶格,其加密由式(3)表示.
| $ {d_j} = {d_j} \oplus {S_2}\left( {u, v, {k_j}} \right) $ | (3) |
END
在式(2)和式(3)中,di和ki分别表示明文和密钥的第i比特,表示异或运算,x和y分别表示di的前一个偶格和后一个偶格.在一般情况下,x和y由式(4)计算.
| $ \left. {\begin{array}{*{20}{l}} {x = {d_{i - 1}}}\\ {y = {d_{i + 1}}} \end{array}} \right\} $ | (4) |
若di位于边界(i=1或i=n),则x或y是di越过边界后的前一个或后一个偶格.类似地,u和v表示dj的前一个和后一个奇格. S1和S2为查找表,其内容在表 1和表 2中显示.解密与加密很相似,但每一轮解密中,应先对全体偶格作解密运算,再对全体奇格作解密运算.由于式(2)和式(3)采用异或运算,解密公式与加密完全相同.
|
|
表 1 查找表S1的内容 |
|
|
表 2 查找表S2的内容 |
由一维加密算法的描述容易得出当格点数为n时,采用串行加密的方式,算法的时间复杂度为O(n2).奇格在加密时,其相邻的偶格均保持不变,因此全体奇格可同时进行加密.同理,全体偶格也可实现并行加密.因此,算法在并行机制下其时间复杂度将大大降低.
2.2 二维数据加密算法二维数据中,各元素排列成矩阵的形式,每个元素仍包含1 bit信息.对二维数据的加密方法可由一维数据的加密扩展而来.首先规定一个元素的邻居是其上、下、左、右4个元素;其次,定义奇格(或偶格)为行下标和列下标之和等于奇数(或偶数)的元素.具体内容在算法D2Enc中描述.
算法名称:D2Enc
输入:
d:待加密的二维数据
k:密钥
输出:
d:加密后的二维数据
过程:
[m, n]=d. size //二维数据的行数和列数
FOR r=1: max(m, n) //加密轮数等于m和n中的较大值
//对全体奇格并行加密.
假设di是一个奇格,其加密由式(5)表示.
| $ {d_i} = {d_i} \oplus S(x, y, u, v) \oplus {k_i} $ | (5) |
//对全体偶格并行加密.
假设dj是一个偶格,其加密由式(6)表示.
| $ {d_j} = {d_j} \oplus S(x, y, u, v) \oplus {k_j} $ | (6) |
END
在式(5)和式(6)中,di和ki分别表示明文和密钥的第i比特,⊕表示异或运算,x、y、u、v分别是与当前元素在上、下、左、右方向上相邻的4个元素.若当前元素位于边界上,则x、y、u、v中的一个或多个值要跨越边界. S是一个查找表,其内容在表 3中显示.与一维数据加密类似,在解密过程的每一轮变换中,应先对偶格解密,再对奇格解密.
|
|
表 3 查找表S的内容 |
根据二维算法的描述可知,串行加密数据的时间复杂度为
Hash函数将变长的输入转换为定长的输出.对D2Enc稍加修改即可构造出二维Hash函数.由于Hash函数是不可逆的,处理时不需区分奇格和偶格,所有元素可并行处理.具体内容在算法D2Hash中描述.
算法名称:D2Hash
输入:
d:二维数据
l:算法输出的比特个数
输出:
h:定长的Hash值
过程:
[m, n]=d. size //二维数据的行数和列数
FOR r=1: max(m, n)
//对全体元素并行处理.假设di是表示第i个元素,其加密由式(7)表示.
| $ {d_i} = {d_i} \oplus S(x, y, u, v) $ | (7) |
END
h=d[1..l] //取处理结果的前l个比特.
2.4 树加密算法与分析设计树的加密算法比一维和二维数据的加密更困难:树没有一维和二维数据那样规整的结构,也没有奇数结点和偶数结点的概念.但是树的加密仍可借鉴易辛模型的思想.由于树有层次的概念,每个结点只与上一层和下一层的结点相连,而同一层的结点互不相连.若把结点按所在层数的奇偶性分成2个集合,则奇数层结点的邻居都在偶数层;反之亦然.由此可以实现对奇数层(或偶数层)上所有结点的并行加密,具体内容在算法TreeEnc中描述.
算法名称:TreeEnc
输入:
t:待加密的树
h:树的高度
k:密钥
输出:
t:加密后的树
过程:
FOR r=1: h //处理轮数等于树的高度
//对奇数层的所有结点并行处理.
设其中某个结点为ti,其处理过程如下:
1) 把ti所有相邻结点的值及密钥k连接成二进制串b;
2) 将b排列成方形矩阵M(若b的长度不是平方数则在b的尾部添0);
3) l=D2Hash(M, 256); //调用D2Hash函数将M转换成256比特的子密钥;
4) ti=D1Enc(ti, l); //调用D1Enc函数对ti进行加密.
//对偶数层的所有结点并行处理,设其中某个结点为tj.
5) 对tj的处理过程与ti完全相同.
END
根据树加密算法的描述,可知树加密算法的时间复杂度取决于算法D1Enc的时间复杂度,故其时间复杂为O(n2).同样,使用并行加密可以提升运算效率.
2.5 图的加密算法及其分析一般的图结构具有不规则性,因此难以判断图中的节点为奇格还是偶格,无法使用易辛模型的处理方式.为此,在设计通用的图加密算法时,将图分为图结构δ和图节点数据m两部分.例如,在表示由n个用户构成的社交网络时,δ是反映n个用户之间相互关系的图形;m包含n个元素,分别对应这n个用户的数据.将δ转换为邻接矩阵,从而使用基于易辛模型的二维数据加密算法进行处理.对于m所表示的节点数据,通过深度优先搜索或广度优先搜索算法,将其转换为树,然后使用树加密算法TreeEnc进行处理.整个图加密的具体内容在算法GraphEnc中描述.
算法名称:GraphEnc
输入:
δ:图结构
m:节点数据
k:密钥
输出:
γ:加密后的图结构
c:加密后的数据
过程:
BEGAN
//图的结构一般用邻接矩阵或邻接表,可转换为二维数据加密;
γ=D2Enc(δ, k);
//节点数据可使用一维数据加密;
c=TreeEnc(m, k);
END
从图加密的过程可以发现,图加密的性能主要由TreeEnc和D2Enc的性能决定,所以,其时间复杂度为O(n2).
3 实验结果 3.1 树加密由于图节点数据加密可以转换为树的加密,实验主要检查树加密算法的随机性和扩散性,前者包括对直方图和相关系数的检测,后者包括对2个扩散性指标的检测.
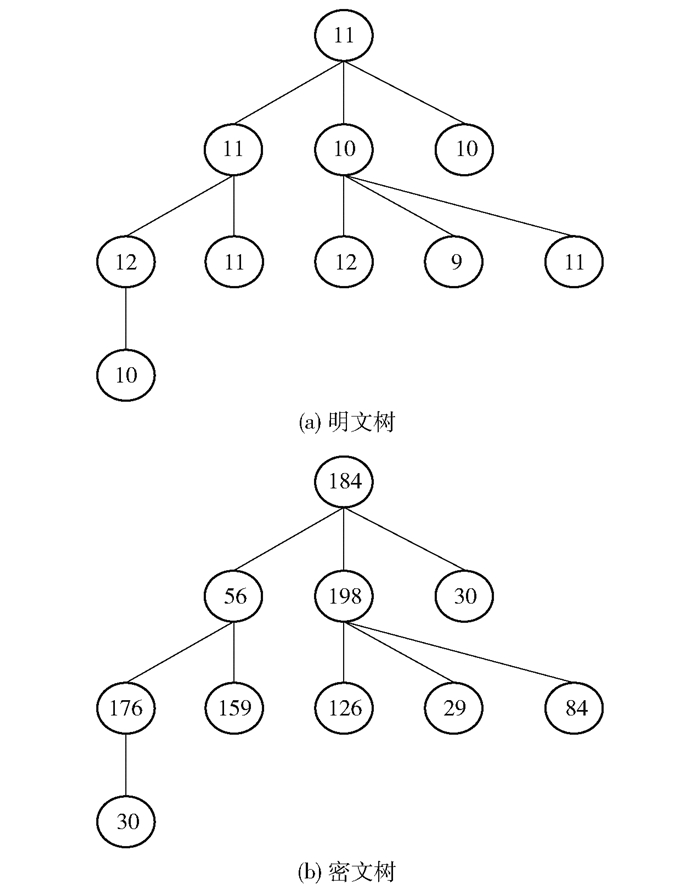
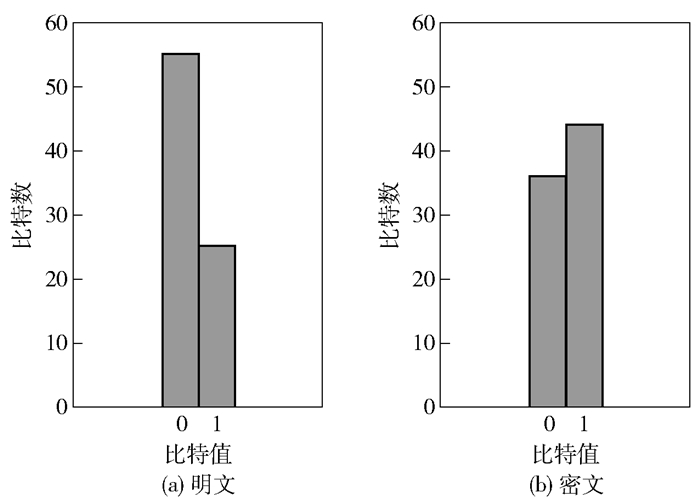
为了直观展示加密效果,对图 2(a)中所示的一棵树的存储结构进行加密.该树的高度为4,共10个节点,每个节点存储1个字节的信息,各节点保存的信息以数值形式展现于图 2(a)中.加密密钥为256 bit的零向量,图 2(b)所示为加密后得到的密文树. 图 3给出了明文和密文的直方图,显然密文的直方图比明文更均匀.这说明加密后,树的分布随机性更高.
|
图 2 树加密示例 |
|
图 3 加密前后的直方图 |
此外,利用相关系数来表征树中父子结点的线性相关程度,其值域为[-1, 1].相关系数的绝对值越大,则相关性越强. 图 2所示的明文树和加密树中,父子节点的平均相关系数为0.608 9和0.002 3,说明笔者设计的加密算法有效地消除了明文中父子结点的线性相关性.
NCR(nodes changing rate)值是从图像加密技术中借用的概念,意指明文某个结点发生改变时,密文结点改变的比例. BCR (bit changing rate)是一个比NCR更严格的概念,指当明文随机改变1 bit时密文各比特的改变率. NCR以结点为单位进行检测,节点以字节为单位时,理想随机树的NCR值为0.996 1;BCR以比特为单位,其检测粒度更细.对于理想随机树,其BCR值为0.5.
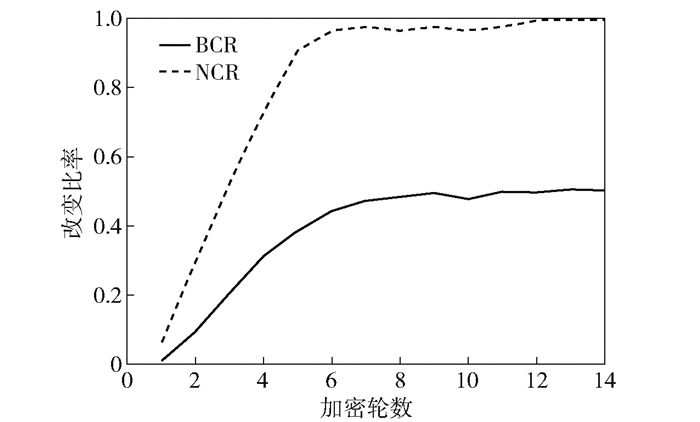
为了显示加密算法扩散过程中的更多细节,随机产生一棵明文树,树的高度为13,包含200个结点,每个结点的长度为1 byte.对该明文树进行加密得到相应的密文树;然后,随机改变明文树中某个结点中的1 bit,再加密改变后的树,得到另一个加密树;最后,根据2个加密树得到树加密算法的NCR和BCR分析结果,如图 4所示. 图 4的结果显示,NCR值和BCR值随加密轮数的增加而增大.当加密进行到第8轮时,NCR和BCR的增长变缓,加密轮次到第11轮时,NCR和BCR值保持在理想值0.996 1和0.5上下轻微波动.测试结果说明,通过在设置合理加密轮数的条件下,本文算法能够达到理想的树加密效果.
|
图 4 高度为13的树在加密过程中NCR值和BCR值变化情况 |
选取斯坦福大学公开数据集CA-GrQc作为加密对象,该数据集展示了一个协作网络,其中包含了5 242个节点和14 496条边.由于图中的节点数据通过树加密算法进行加密,其性能已在3.3节中进行了分析,所以本节只展示对图结构进行加密的效果.选取数据集中第10~1 500节点之间的结构进行加密. 图 5(a)所示为加密前从数据集中随机选取10个节点所得到的这些节点之间的连接情况,图 5(b)为加密后,这10个节点之间的连接情况.对比图 5(a)和(b)可以看出,加密算法很好地隐藏了图结构.为了从整体上展示对图结构的加密效果,将第10~1 500节点之间的连接关系用邻接矩阵的方式表示,再将此邻接矩阵转化为二值图像,如图 6(a)所示.其中,图像中的黑色点和白色点分别表示对应节点之间存在和不存在邻接关系.对图结构加密之后,邻接矩阵对应的二值图像如图 6(b)所示.根据图 6可以看出,加密后的图结构边分布趋于均匀,很好地隐藏了原始的图结构.

|
图 5 图加密 |

|
图 6 结构二值图 |
图的加密具有广泛而重要的应用.笔者对易辛模型进行了改造,并设计了一维数据和二维数据的加密算法,进而构成树加密算法.所提出的图加密算法将图分为图结构和图节点数据2个部分,分别使用二维数据和树加密算法进行加密.理论分析和实验测试的结果表明,所提出的方法可以满足图加密的各项要求.这说明将易辛模型用于图加密这一思路是可行的.现阶段的研究是基于易辛模型,以比特为单位设计的图加密算法,在未来的工作中将继续研究以字节为单位的加密算法,进一步提高算法的效率.
| [1] |
Ślusarczyk G, Łachwa A, Palacz W, et al. An extended hierarchical graph-based building model for design and engineering problems[J]. Automation in Construction, 2017(74): 95-102. |
| [2] |
Luo C, Zuo L. Metric properties of Sierpin' ski-like graphs[J]. Applied Mathematics and Computation, 2017(296): 124-136. |
| [3] |
Lin M S, Chen C M. Counting independent sets in tree convex bipartite graphs[J]. Discrete Applied Mathematics, 2017(218): 113-122. |
| [4] |
Zhou H, Li J, Li J, et al. A graph clustering method for community detection in complex networks[J]. Physica a:Statistical Mechanics and Its Applications, 2017(469): 551-562. |
| [5] |
Fortunato S. Community detection in graphs[J]. Physics Reports, 2010, 486(3-5): 75-174. DOI:10.1016/j.physrep.2009.11.002 |
| [6] |
Ising E. Beitrag zur theorie des ferromagnetismus[J]. Zeitschrift für Physik, 1925, 31(1): 253-258. DOI:10.1007/BF02980577 |


