针对低信噪比(SNR)和复杂电磁环境条件下跳频参数估计精度低及算法复杂度高的问题,提出了一种短时傅里叶变换(STFT)和平滑伪魏格纳分布(SPWVD)的组合时频分析方法.该算法首先利用STFT将天线接收信号变换到时频域,并对时频信号进行自适应降噪处理;通过自适应聚类算法进行频率的精估计;提取时频信息并剔除各类干扰,再通过网台分选后得到各类网台跳时粗估计;最后采用SPWVD及修正后的截断门限进行跳变时刻的精估计.仿真结果表明,该算法在混合网台和低SNR条件下,跳频参数估计精度较高,算法复杂度较低,有效解决了实际跳频通信系统存在频率转换时间条件下的参数估计问题.
To solve low accuracy of parameter estimation and high complexity of algorithms in frequency hopping signal under low signal-to-noise ratio (SNR) and complex electromagnetic environment, a new algorithm combined short-time Fourier transform (STFT) with smoothed pseudo Winger-Ville distribution (SPWVD) is proposed. Firstly, the received signals are converted to time-frequency domain by using STFT, and then adaptive noise reduction is used in time-frequency domain. Secondly, the accurate frequency is estimated by adaptive clustering algorithm. Thirdly, the time-frequency information of the signals is extracted and all kinds of interference are eliminated. After the network is sorted, the rough estimation range of the hopping time can be calculated. Finally, SPWVD algorithm and a truncation threshold are used to deal with the rough estimation range, and then a precise frequency estimation is obtained. Simulations show that the parameter estimation of the algorithm has high accuracy and low complexity under the condition of hybrid networking and low SNR. The parameter estimation problem of existing frequency switching time in actual frequency hoppingcommunication system has been effectively solved.
跳频信号具有抗干扰和抗衰落能力强、截获率低和易于实现多址组网等特点, 因而广泛地应用在无线通信领域[1-3], 同时也向通信对抗侦查提出了严峻的挑战[4].参数估计是跳频信号侦查的一个关键步骤, 经典的时频分析方法主要有短时傅里叶变换(STFT, short-time Fourier transform)[5]、Gabor变换[6]、魏格纳分布、平滑伪魏格纳分布(SPWVD, smoothed pseudo Winger-Ville distribution)[7-9]等.张坤峰等[10]和Zhao等[11]提出的跳频参数估计方法都只考虑单个跳频信号, 不适用于多个跳频信号的情况.付卫红等[12]提出的组合时频分析方法只适用于同步网台且能量分布均匀的条件下, 该方法对同步网台的参数估计效果较好.然而在战场环境中, 存在大量的噪声干扰, 大多数情况下都是混合网台(既有同步网台又有异步网台称为混合网台).陈利虎等[13]提出的谱图时频矩阵和SPWVD“相乘”得到信号的时频图后, 分别沿频率轴及时间轴投影寻找峰值, 再修正峰值位置, 将得到的准确的峰值位置分别作为载频以及跳变时刻的估计值.该方法对全部时域观测信号进行SPWVD变换, 算法复杂度高, 且信噪比(SNR, signal-to-noise ratio)低时, 时频峰值检测困难, 跳周期估计误差性能差.从上面的分析可以看出, 单一跳频信号和同步网台的参数估计技术比较成熟, 但对混合网台且存在频率转换时间的情形研究较少.因此, 当考虑频率转换时间时, 一个源信号的每两跳之间都需要估计出2个跳变时刻, 分别为终止时刻和起始时刻(终止时刻表示前一跳的截止时刻, 起始时刻表示后一跳的起跳时刻).对一般算法而言, 2个跳变时刻的估计, 不仅仅是增加了算法的复杂度, 而且使很多算法直接失效.
所以针对上述问题, 笔者提出了基于STFT-SPWVD的组合时频分析方法, 不但考虑频率转换时间、低SNR和复杂电磁环境, 而且在混合网台参数估计中, 参数估计的精度较高, 算法的复杂度较低.
1 跳频信号模型跳频信号的载频由一组伪随机码控制在一个宽频带内进行随机跳变, 其模型可定义为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{s}}_i}\left( t \right) = \sqrt S \exp \left[ {{\rm{j}}\left( {2{\rm{ \mathsf{ π} }}{f_0}t + {\varphi _0}} \right)} \right]{\rm{rect}}\left( {\frac{t}{{\Delta {t_0}}}} \right) + }\\ {\sum\limits_{l = 1}^L {\exp } \left[ {{\rm{j}}\left( {2{\rm{ \mathsf{ π} }}{f_l}t + {\varphi _l}} \right)} \right]{\rm{rect}}\left( {\frac{{t - \left( {l - 1} \right){T_c} - \Delta {t_0}}}{{{T_c}}}} \right) + }\\ {\exp \left[ {{\rm{j}}\left( {2{\rm{ \mathsf{ π} }}{f_E}t + {\varphi _E}} \right)} \right]{\rm{rect}}\left( {\frac{{t - L{T_c} - \Delta {t_0}}}{{\Delta {t_E}}}} \right)} \end{array} $ | (1) |
其中: si(t)为第i个源信号;
| $ K = \frac{{{T_c}}}{{{T_c} + T'}} $ | (2) |
当考虑附加高斯白噪声的影响时, 跳频通信系统数学模型为
| $ \mathit{\boldsymbol{x}}\left( t \right) = \mathit{\boldsymbol{A}}\left( t \right)\mathit{\boldsymbol{s}}\left( t \right) + \mathit{\boldsymbol{n}}\left( t \right) $ | (3) |
其中:s(t)=[s1(t), s2(t), …, sn(t)]T为发送信号矢量; A=[α1, α2, …, αn]为m×n的天线增益矩阵(m≥n), 矩阵A也称为混合矩阵; n(t)为正态分布的复高斯白噪声.
2 算法原理首先使用STFT将天线接收信号变换到时频域, 并对时频信号进行自适应降噪处理; 其次通过自适应聚类算法进行频率的精估计, 剔除各类干扰后并分选混合网台; 然后提取时频信息得到跳时粗估计; 最后采用SPWVD及修正后的截断门限进行跳变时刻的精估计.
2.1 基于STFT算法的时频信息处理对采样信号x(t)进行STFT, 重叠窗长为3P/4(P为STFT的窗长), 得到时频信号X(t, f).
为了避免噪声的影响, 对时频信号X(t, f)自适应降噪.首先找到所有时频点幅度的最小值X1以及最大值X2, 然后得到阈值的一个初值ε1=(X1+X2)/2.以ε1为时频支撑点阈值, 将所有时频点分为2部分:当|X(t, f)|>ε1时, 存于F1中, 并统计其频点个数记为
| $ \left. \begin{array}{l} X' = \sum\limits_{\mathit{\boldsymbol{X}}\left( {t,f} \right) \in {F_1}} {\frac{{\left| {\boldsymbol{X}\left( {t,f} \right)} \right|}}{{{{\tilde N}_1}}}} \\ X'' = \sum\limits_{\mathit{\boldsymbol{X}}\left( {t,f} \right) \in {F_2}} {\frac{{\left| {\boldsymbol{X}\left( {t,f} \right)} \right|}}{{{{\tilde N}_2}}}} \end{array} \right\} $ | (4) |
根据2个频点幅度模值, 计算出新的阈值.重复上述过程直到第k次迭代的阈值εk与第k+1次迭代的阈值εk+1满足|εk-εk+1| < 0.1时停止迭代, 得到稳定的阈值ε=εk+1, 将大于阈值的时频点保留, 小于阈值的时频点置零, 最终得到
为了提高频率的分辨率, 首先采用自适应聚类算法对时频图中的频率进行聚类, 对
| $ {\mathit{\boldsymbol{f}}_l} = \frac{{\mathit{\boldsymbol{l}}{f_s}}}{P} $ | (5) |
其中fs为采样频率.通过式(5)获得fl后, 对fl中所有的元素进行聚类, 得到第l列即第l窗的聚类载频flo=[flo(1) flo(2) … flo(γl)], 其中γl为第l窗所聚载频个数.
得到各个窗的聚类频率flo后, 统计每个频率fi的起始窗tsi、终止窗tei以及持续窗数ti(ti=tei-tsi+1), 用向量Ti表示, Ti=(fi, tsi, tei, ti).
由于在短波频段电磁环境十分复杂, 各种信号分布密集而且种类较多, 因此, 在提取时频信息以后, 需要对信号中的干扰信号进行检测并进行干扰剔除.
下面进行干扰类型分析并提出对于不同干扰类型的剔除方法.
1) 定频信号检测及剔除:定频信号又分为连续定频信号和断续定频信号.
连续定频信号检测及剔除:对每一跳载频的时频信息Ti进行判断, 当持续窗数ti>3L(其中L为所有载频的平均持续窗数)时, 说明该跳为连续定频信号, 将该跳时频信息进行剔除.
断续定频信号检测及剔除:对时频信息Ti中每个频率fi使用的次数进行统计, 并求出平均使用次数记为nf, 当某个频率的使用次数大于3nf时, 则认为该频率所对应的时频信息为断续定频信号, 需要剔除.
2) 扫频信号检测及剔除:由于扫频信号占用的带宽较宽, 且相对稳定, 而跳频信号带宽较窄, 通过对时频信息的聚类, 扫频信号不显现频率聚类特性, 而跳频信号将会在载频处出现聚类中心, 因此, 可通过聚类方法去除扫频干扰.
3) 突发信号剔除:如果突发信号的频率随时间在变化, 可按扫频信号的处理方法剔除, 否则通过统计跳频信号的驻留时间, 用驻留时间为标准, 直接剔除; 如果按驻留时间不能剔除, 则可按照不同频点上信号段之间不存在连续性而予以剔除.
剔除各类干扰以后, 按照持续窗数ti对时频信息进行分类, 并且按照起始窗tsi出现的时间进行排序.对于每一类信号分别进行处理(类内同步信号可当作单一跳频信号处理), 对于类内的每两跳信号之间, 前一跳信号的终止窗为tek, 后一跳信号的起始窗为tsk+1, 则跳变时刻的粗估计范围为
| $ {\mathit{\boldsymbol{y}}_k} = \mathit{\boldsymbol{x}}\left( {\left( {t_e^k - 1} \right)\frac{P}{4}:\left( {t_s^{k + 1} + 1} \right)\frac{P}{4}} \right) $ | (6) |
其中k=1, 2, …, m, m为跳变点的个数.
虽然魏格纳分布、伪魏格纳分布时频聚焦性强, 但是都属于二次时频分析方法, 易受到交叉项的干扰, 严重影响参数估计的性能.因此采用SPWVD算法, 时频域同时加窗, 从而抑制交叉项的干扰. SPWVD的定义为
| $ \begin{array}{*{20}{c}} {\int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } \boldsymbol{x} } } \left( {u + \frac{\tau }{2}} \right){\boldsymbol{x}^*}\left( {u - \frac{\tau }{2}} \right)\psi \left( {\tau ,v} \right) \times }\\ {{{\rm{e}}^{ - {\rm{j}}2{\rm{ \mathsf{ π} }}\left( {tv + tf - uv} \right)}}{\rm{d}}u{\rm{d}}v{\rm{d}}\tau } \end{array} $ | (7) |
其中ψ(t, v)为时频域的平滑函数.
根据上述原理, 分别对截取信号yk进行SPWVD变换, 得到其时频矩阵Yk(t, f).再对时频矩阵Yk(t, f)进行截断处理, 得到截断处理后的时频矩阵Y′k(t, f):
| $ {{\mathit{\boldsymbol{Y'}}}_k}\left( {t,f} \right) = \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{Y}}_k}\left( {t,f} \right),}&{若\;\left| {{\mathit{\boldsymbol{Y}}_k}\left( {t,f} \right)} \right| > \delta }\\ {0,}&{若\left| {{\mathit{\boldsymbol{Y}}_k}\left( {t,f} \right)} \right| < \delta } \end{array}} \right. $ | (8) |
其中δ为截断门限.在文献[13]中, 截断门限设置为δ=η×mean(Yk(t, f)), 通过设置η来设置截断门限, 该方法易导致截断门限偏大或偏小.当截断门限设置较小时, 导致对应载频信息的长度偏长; 当截断门限设置较大时, 导致对应载频信息长度偏短.针对此问题, 提出一种基于精估计出的频率修正截断门限的方法, 通过精估计频率, 找到该频率在时频矩阵Y′k(t, f)中的位置, 获取该频率对应时频矩阵中的幅值, 绝对值求和取平均作为截断门限.该方法降低了非载频信息点对截断门限设置的影响, 其具体方案如下:
设第k个截取信号的采样点数为Nk, 当估计跳频信号的前一跳终止时刻时, 其对应载频位置为n1=Pfk1/fs(fk1为yk前一跳的频率, fs为采样频率); 当估计跳频信号的后一跳起始时刻时, 其对应载频位置为n2=Pfk2/fs(fk2为yk后一跳的频率).则此时的截断门限为
| $ {\delta _r} = \frac{1}{{{N_k}}}\sum\limits_{j = 1}^{{N_k}} {\left| {{\mathit{\boldsymbol{Y}}_k}\left( {j,{n_r}} \right)} \right|} ,\;\;\;r = 1,2 $ | (9) |
截断信号yk的前一跳终止时刻为hk1=max(t||Y′k(t, fk1)|>0), 后一跳起始时刻为hk2=min(t||Y′k(t, fk2)|>0)(由于SPWVD的滑窗长度为1, 因此窗数和时刻点数一一对应).
实际的跳时精估计为
| $ \left. \begin{array}{l} {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over h} }_{k,1}} = \left( {t_e^k - 1} \right)\frac{P}{4} + {h_{k1}}\\ {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over h} }_{k,2}} = \left( {t_s^{k + 1} - 1} \right)\frac{P}{4} + {h_{k2}} \end{array} \right\} $ | (10) |
则跳周期为
| $ {{\hat T}_{{\rm{hop}}}} = \left( {{\rm{mean}}\left( {{{\hat h}_{k,1}} - {{\hat h}_{k - 1,1}}} \right) + {\rm{mean}}\left( {{{\hat h}_{k,2}} - {{\hat h}_{k - 1,2}}} \right)} \right)/2 $ | (11) |
实验1 不同算法的跳频信号参数估计性能
参数设置:仿真使用3个跳频信号, 采用同步异步共存的混合组网方式, 不考虑跳频信号之间的碰撞, 符号速率分别为200 kbit/s、200 kbit/s、160 kbit/s, 跳频图案分别为
| $ {s_1} = \left\{ {\begin{array}{*{20}{c}} {26.5}&{30}&{33}&{28}&{34} \end{array}} \right\} $ |
| $ {s_2} = \left\{ {\begin{array}{*{20}{c}} {31.5}&{35.5}&{30.5}&{27}&{33} \end{array}} \right\} $ |
| $ {s_3} = \left\{ {\begin{array}{*{20}{c}} {24.5}&{21}&{26}&{22} \end{array}} \right\} $ |
其中:s1、s2为同步信号, s3为异步信号.占空比K=0.92, 采样率fs=80 MHz, STFT窗长P=3 200, 滑动窗长为
由图 1、图 2、图 3可知:文献[5]算法中跳时刻估计精度较低, 由于STFT参数估计的过程是一个不断滑窗的过程, 所以只能估计出跳频信号在哪一个窗内发生跳变, 并不能准确地估计出跳变时刻, 导致估计误差较大.该算法通过查找时频幅值的最大值来估计跳频频率, 但是在实际的跳频通信系统中, 跳频信号的频率分辨率往往受限, 因此该仿真实验固定了频率分辨率, 而且当相同频率在不同时间重复出现时, 导致采用时频峰值估计出现较大误差, 甚至出现估计出的频率个数少于实际载频数.
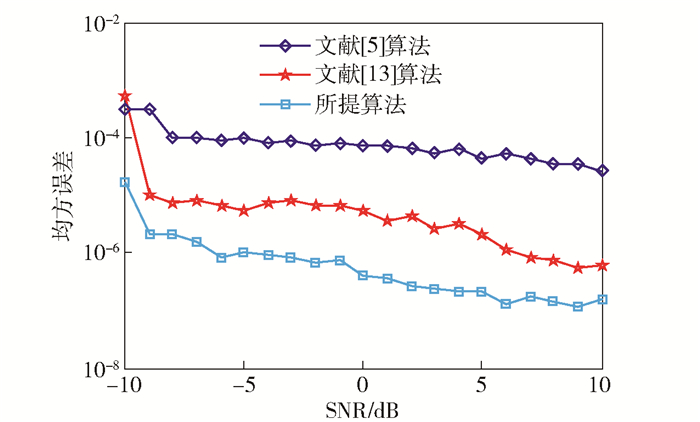
|
图 1 跳时刻均方误差估计 |
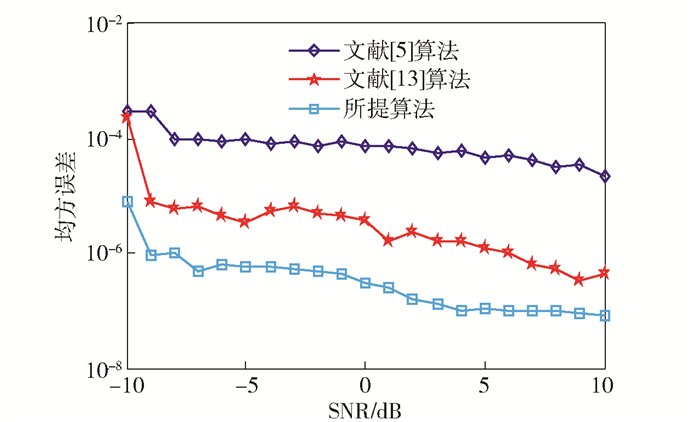
|
图 2 跳周期均方误差估计 |
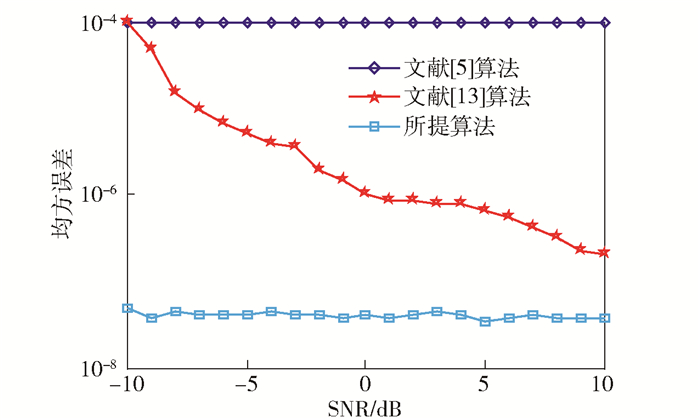
|
图 3 跳频频率均方误差估计 |
文献[13]中的算法跳时刻估计在得到时频图后, 分别沿频率轴及时间轴投影寻找峰值, 再修正峰值位置, 将得到准确的峰值位置分别作为载频以及跳变时刻的估计值.该方法受噪声影响严重, 当SNR较低时, 时频峰值检测困难, 跳周期估计误差性能差, 导致算法参数估计精度较低.
所提算法得到的跳频信号参数估计性能较好, 是由于所提算法通过时频域的自适应降噪, 增强了该算法的抗噪性能.虽然都在相同的频率分辨率条件下进行仿真, 笔者采用时频域的频率聚类的方法, 增加了频率的聚集性, 提高了频率的分辨率.另外, 在使用SPWVD算法时, 由于截取的跳时粗估计信号较短, 设置滑动步长B=1, 提高了时间分辨率.在估计跳变时刻时, 根据精估计的频率, 设置了自适应的截断门限, 精估计出跳时刻.因此, 所提算法的跳频信号参数估计精度较高.
实验2 非均匀能量分布对跳频信号参数性能的影响
参数设置:3个同步信号的跳频图案分别为
| $ {s_1} = \left\{ {\begin{array}{*{20}{c}} {26.5}&{30}&{33}&{28}&{34} \end{array}} \right\} $ |
| $ {s_2} = \left\{ {\begin{array}{*{20}{c}} {31.5}&{35.5}&{30.5}&{27}&{33} \end{array}} \right\} $ |
| $ {s_3} = \left\{ {\begin{array}{*{20}{c}} {24.5}&{21}&{26}&{22}&{36} \end{array}} \right\} $ |
且能量均匀时Ps1:Ps2:Ps3=1::11, 能量非均匀时Ps1:Ps2:Ps3=10:5:1, 跳速分别为h1=2 000 hop/s、h2=2 000 hop/s、h3=2 000 hop/s, 入网时间分别为0.125 ms、0.125 ms、0.125 ms, 其余条件与仿真实验1相同.
由于文献[12]中的算法只适用于同步网台的跳频信号参数估计, 且对能量分布敏感, 所以在此次仿真中, 只用同步信号, 单独和所提算法进行对比.
由图 4可以看出, 文献[12]中的算法跳时估计受源信号的能量分布影响严重, 其主要原因是该算法将同步信号当作一跳处理, 每一跳选取一个载频, 当所取信号的前一跳和后一跳来自同一个源信号时, 采用主能量分析法, 认为主要能量分布在2个不同的载频上, 判断为此处发生跳变; 当所取信号的前一跳和后一跳来自2个不同的源信号, 且能量分布差别较大时, 主能量仍然集中在一个频率上, 该算法认为没有发生跳变, 因此在能量分布非均匀且能量分布差别较大时, 跳时估计误差较大.

|
图 4 文献[12]算法随信号能量分布影响 |
由图 5可以看出, 所提出算法受能量干扰较小, 因为即便源信号的能量分布差别较大, 但是时频矩阵中的载频位置的信息估计不受影响, 仍然可以通过频率聚类得到信号的频率估计, 统计载频的起始时间、终止时间以及持续窗长, 都与能量分布无关, 根据提取的时频信息, 粗估计得到跳变时刻, 通过SPWVD对粗估计的信号进行处理, 根据估计出的频率设置截断门限, 最终得到精估计的跳时.因此, 所提算法受源信号的能量分布影响较小.
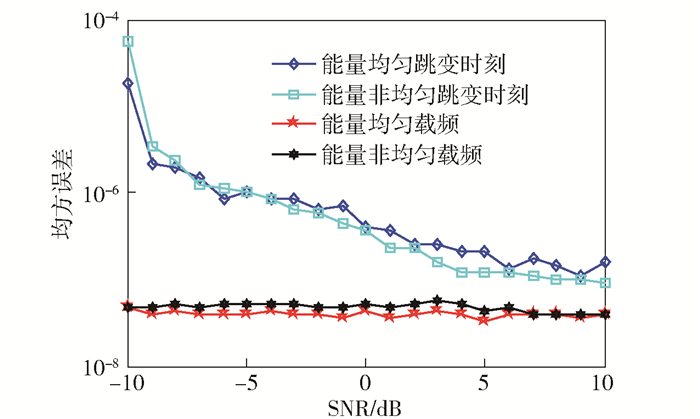
|
图 5 所提算法随信号能量分布影响 |
实验3 复杂电磁环境下多跳频信号网台分选
参数设置:7个源信号的参数设置为
| $ {s_1} = \left\{ {\begin{array}{*{20}{c}} {30}&{21}&{8.5}&{30.5}&{28} \end{array}} \right\} $ |
| $ {s_2} = \left\{ {\begin{array}{*{20}{c}} {12}&{35.5}&{19.5}&{7.5}&{30} \end{array}} \right\} $ |
| $ {s_3} = \left\{ {\begin{array}{*{20}{c}} {25}&8&{34.5}&{36}&{21.5} \end{array}} \right\} $ |
| $ {s_4} = \left\{ {\begin{array}{*{20}{c}} {21.5}&{36.5}&{22}&{37.5} \end{array}} \right\} $ |
| $ {s_5} = \left\{ {\begin{array}{*{20}{c}} {33}&{23.5}&{26.5}&{20} \end{array}} \right\} $ |
| $ {s_6} = \left\{ {\begin{array}{*{20}{c}} {31}&{32}&7&{16} \end{array}} \right\} $ |
| $ {s_7} = \left\{ {\begin{array}{*{20}{c}} {35}&{16.5}&{36.5}&{39}&{35}&5&{7.5} \end{array}} \right\} $ |
其中:s1、s2、s3属于一个同步网台, s4、s5、s6属于一个同步网台, s7属于一个异步网台.跳速分别为h1=2 000 hop/s、h2=2 000 hop/s、h3=2 000 hop/s、h4=1 500 hop/s、h5=1 500 hop/s、h6= 1 500 hop/s、h7=2 500 hop/s, 符号速率分别为b1=200 kbit/s、b2=200 kbit/s、b3=200 kbit/s、b4=160 kbit/s、b5=160 kbit/s、b6=160 kbit/s、b7=250 kbit/s, 入网时间分别为0.125 ms、0.125 ms、0.125 ms、0.25 ms、0.25 ms、0.25 ms、0.187 5 ms, 信号的入射角度分别为-66°、-56°、60°、-36°、16°、-16°、-6°, 其余参数和仿真实验1相同.
为了考虑复杂电磁环境和多个网台条件下所提算法性能, 增加了扫频信号、连续定频信号和断续定频信号, 经过所提算法自适应降噪后得到稳定的时频信息如图 6所示, 经过干扰剔除后, 转换成无干扰类型, 再进行跳频参数估计, 由图 7可以看出, 跳时、跳频和跳周期仍然有较高的估计精度.
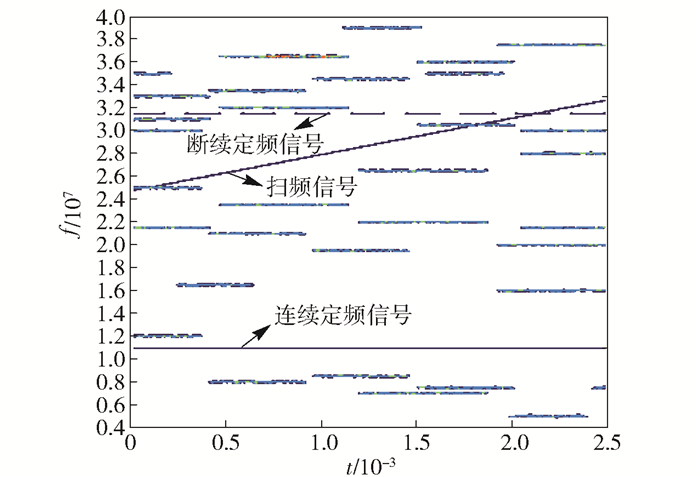
|
图 6 混合自适应降噪后的时频图 |

|
图 7 多个网台在复杂电磁环境下的参数估计 |
为了表示方便, 用N表示总的信号的采样长度, Nk表示SPWVD第k次粗估计的截取的信号长度,
由于计算算法复杂度时, 加法的次数相对乘法的次数可以忽略不计, 所以在这里只考虑乘法次数.所提出的STFT算法复杂度为
参数设置为:N=2×105、P=3 200、K=0.92、A=7, STFT重叠窗长为P/4, 虽然每次粗估计信号的长度有略微差异, 但基本稳定在5 000个点左右, 因此M=5 000, 自适应降噪的迭代次数经过多次测试, 基本在60次左右即可迭代完成, 则C=60, W=790 400, 得到具体算法次数详见表 1.
|
|
表 1 不同算法的运算量(乘法次数) |
在相同硬件和给定SNR条件下, 使用仿真实验1中的参数, 仿真所提出的STFT-SPWVD算法时用时50.774 0 s, 仿真文献[13]中的谱图-SPWVD, 由于算法复杂度太高, 同等硬件无法仿真, 只能增大谱图和SPWVD的滑窗间隔, 滑窗间隔设置为B2=64, 最终用时174.41 s.从上述数据可以看出, 由于仿真点数较多, 所以算法复杂度都较高, 但是, 在相同的参数设置条件下, 所提出的算法比文献[13]中的算法复杂度降低了6个数量级.当文献[13]中的算法的滑窗间隔B2=64时, 由图 1和图 3可以看出, 所提算法比文献[13]中的算法的跳时均方误差估计低1个数量级, 跳频频率均方误差估计低3个数量级.而且由表 1可以看出, 所提算法复杂度比文献[13]中的算法低4个数量级.
5 结束语笔者提出了一种基于STFT-SPWVD组合的时频分析方法, 并结合跳频信号的结构特性, 考虑频率转换时间和混合组网方式, 解决了现有算法在低SNR和复杂电磁环境条件下跳频参数估计精度低及算法复杂度高的问题.本算法利用STFT复杂度低的特点对跳频信号进行粗估计, 使用自适应聚类算法对频率进行聚类, 提高了频率的分辨率, 再根据各类干扰的特性进行干扰剔除, 并结合SPWVD算法估计精度高的特点以及截断门限的修正, 不仅提高了跳时的估计精度, 而且还避免了对整个信号进行SPWVD处理带来的高复杂度的影响.最后通过仿真实验证明了所提算法不仅受源信号能量分布影响较小, 在相同的条件下比现有谱图-SPWVD算法复杂度降低6个数量级, 而且跳时均方误差估计降低了1个数量级, 跳频频率均方误差估计降低了3个数量级.
| [1] |
付卫红, 武少豪, 刘乃安, 等. 跳频信号的欠定盲源分离[J]. 北京邮电大学学报, 2015, 38(6): 11-14. Fu Weihong, Wu Shaohao, Liu Naian, et al. Underdetermined blind source separation of frequency hopping signal[J]. Journal of Beijing University of Posts and Telecommunications, 2015, 38(6): 11-14. |
| [2] |
Sousa J S, Vilela J P. Uncoordinated frequency hopping for wireless secrecy against non-degraded eavesdroppers[J]. IEEE Transactions on Information Forensics & Security, 2017, 13(1): 143-155. |
| [3] |
Rothman T. Random paths to frequency hopping[J]. American Scientist, 2019, 107(1): 46-53. DOI:10.1511/2019.107.1.46 |
| [4] |
孟令杰, 张顺健, 翟翔. 战术电台跳频通信反侦察抗干扰效能分析[J]. 火力与指挥控制, 2018, 43(6): 76-80. Meng Lingjie, Zhang Shunjian, Zhai Xiang. Analysis of counter-reconnaissance and counter-jamming effectiveness for tactical radio frequency hopping communication[J]. Fire Control & Command Control, 2018, 43(6): 76-80. DOI:10.3969/j.issn.1002-0640.2018.06.015 |
| [5] |
胡杨林, 金燕华.跳频信号盲检测与参数盲估计算法研究及实现[D].成都: 电子科技大学, 2016: 28-51. http://cdmd.cnki.com.cn/Article/CDMD-10614-1016176029.htm
|
| [6] |
于欣永, 郭英, 张坤峰, 等. 基于盲源分离的多跳频信号网台分选算法[J]. 信号处理, 2017, 33(8): 1082-1089. Yu Xinyong, Guo Ying, Zhang Kunfeng, et al. A network sorting algorithm based on blind source separation of multi-FH signal[J]. Journal of Signal Processing, 2017, 33(8): 1082-1089. |
| [7] |
Stevens D L, Schuckers S A. Low probability of intercept frequency hopping signal characterization comparison using the Wigner Ville distribution and the Choi Williams distribution[J]. Global Journal of Research In Engineering, 2016, 16(2): 2249-2596. |
| [8] |
张承骥, 桂志先, 王鹏, 等. 基于Renyi熵的SPWVD时频参数优选研究[J]. 能源与环保, 2017, 39(2): 32-35. Zhang Chengji, Gui Zhixian, Wang Peng, et al. Study on optimization selection of SPWVD parameters based on Renyi entropy[J]. China Energy and Environmental Protection, 2017, 39(2): 32-35. |
| [9] |
Liang Zhongjie, Lü Ming. A joint rapid parameter estimate method of frequency hopping signals[C]//2012 International Conference on Control Engineering and Communication Technology. Washington: IEEE, 2012: 952-954.
|
| [10] |
张坤峰, 郭英, 齐子森, 等. 基于稀疏贝叶斯重构的多跳频信号参数估计[J]. 华中科技大学学报(自然科学版), 2017, 45(1): 97-102. Zhang Kunfeng, Guo Ying, Qi Zisen, et al. Parameter estimation for multiple frequency-hopping signals based on sparse Bayesian reconstruction[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2017, 45(1): 97-102. |
| [11] |
Zhao L, Wang L, Bi G, et al. Robust frequency-hopping spectrum estimation based on sparse bayesian method[J]. IEEE Transactions on Wireless Communications, 2015, 14(2): 781-793. DOI:10.1109/TWC.2014.2360191 |
| [12] |
付卫红, 王璐, 贾坤, 等. 基于STFT与SPWVD的跳频参数盲估计算法[J]. 华中科技大学学报(自然科学版), 2014(9): 59-63. Fu Weihong, Wang Lu, Jia kun, et al. Blind parameter estimation algorithm for frequency hopping signals based on STFT and SPWVD[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2014(9): 59-63. |
| [13] |
陈利虎, 张尔扬. 一种多分量跳频信号参数盲估计方法[J]. 信号处理, 2009, 25(2): 194-198. Chen Lihu, Zhang Eryang. A new method for blind parameter estimation of multicomponent frequency-hopping signals[J]. Journal of Signal Processing, 2009, 25(2): 194-198. DOI:10.3969/j.issn.1003-0530.2009.02.006 |



