2. 景德镇陶瓷大学 机电学院, 江西 景德镇 333000;
3. 深圳网络空间科学与技术广东省实验室(鹏城实验室), 广东 深圳 518055
为满足差异化业务场景下不同类型用户的服务质量需求,构建了基于网络切片的无线资源分配模型.为获得最佳资源调度方案,将用户服务质量需求转化为无线资源需求,以系统总速率最大化为目标,构建网络资源管理和分配机理及其优化问题.该优化问题为混合整数非线性规划,直接求解复杂度较高,因此提出了基于拉格朗日对偶理论的解决方案,并给出求解算法.通过与比例公平算法和最大系统容量算法进行对比及仿真分析,证明了所提算法在牺牲了部分公平性的前提下提高了系统容量,并验证了所提算法的有效性.
2. School of Mechanical and Electronic Engineering, Jingdezhen Ceramic Institute, Jiangxi Jingdezhen 333000, China;
3. Shenzhen Cyberspace Laboratory, Guangdong Shenzhen 518055, China
In order to meet the quality of service requirements of different types of users in different application scenarios and improve spectrum efficiency, the wireless resource allocation model is constructed based on network slicing. In order to obtain the optimal resource allocation scheme, the quality of service requirements of users are transformed into the wireless resources requirements, and the wireless resource optimization problem is formulated with the goal of maximizing the total system rate. Since the optimization is a mixed integer nonlinear optimization, the complexity of optimal solution is considerably high. A solution based on Lagrange duality is proposed and the solving algorithm is given. Finally, compared with the proportional fairness algorithm and the maximum system capacity algorithm, the simulation results show that the proposed algorithm improves the system capacity while sacrificing partial fairness, which verifies the effectiveness of the proposed algorithm.
随着移动互联网和物联网的快速发展, 产生了如超高清视频、虚拟现实、智能抄表、智能家居、车联网等多样化的业务场景, 终端的接入数目、种类和流量发生了爆炸式增长.业务类型的丰富多样导致其业务特征差异巨大, 如智能家居和环境监测等业务需要网络对海量连接设备的支持; 超高清视频和移动医疗则对速率的性能要求较高; 车联网和工业控制则对时延和可靠性的要求极高.由此可看出, 不同业务场景对数据传输速率、时延、可靠性和连接密度等性能指标有不同的要求.当前第4代移动通信系统网络架构只能满足传统移动用户的单一业务需求, 无法满足多样化业务场景要求, 因此迫切需要发展下一代移动通信网络.
5G移动通信网络将会支持和扩展更多的差异化业务场景, 并定义了3大类业务场景:增强移动宽带(eMBB, enhanced mobile broadband)、海量机器类通信(mMTC, massive machine type communication)和超可靠低时延通信(uRLLC, Ultra-reliable-low latency Communications)[1], 这3大类业务场景涵盖了当下和未来发展的所有典型业务场景.而未来5G对这3类业务的支持是依靠其关键技术之一的网络切片(NS, Network slicing)[2]. NS可看作对物理网络进行切分, 并按照业务需求构建端到端的逻辑网络, 为差异化业务提供定制化服务. NS由多种网络功能组成, 并依靠必要的物理资源或虚拟资源保持正常运行[3].不同NS对应不同的业务场景, 并对其用户提供服务需求, 同时, 不同类型业务的用户其性能要求差异较大, 对应的资源种类及数量要求自然不同. NS为用户提供服务时需要合适的资源作为支撑, 过多的资源导致资源浪费, 且降低了频谱效率, 过少的资源影响NS性能, 且降低用户服务质量.在多种资源中, 无线通信资源对NS影响最为直接, 因为无线通信资源量较少且信道条件恶劣, 直接影响NS服务用户的服务质量, 所以无线通信资源的合理分配对NS的正常运行和用户的服务质量至关重要.
许多学者以最大频谱效率为目标研究资源管理. Parsaeefard等[4]基于无线虚拟化网络对资源管理和接入控制进行了研究, 建立了最小资源约束和最小速率约束的两种虚拟网络要求, 在资源有限的前提下建立优化问题来求解最优的子信道和功率分配.为满足不同服务提供商对用户提供的服务和用户之间的公平性, Kamel等[5]建立相应的优化问题, 由于其为NP-hard问题, 较难求解, 所以提出了一种有效的启发式算法来求次优解. Parsaeefard[6]不仅考虑子信道和功率的分配, 而且将用户对基站的选择纳入其中, 并提出了低复杂度的两步迭代算法求最优解.
为节约能量, 许多学者开始考虑以最大能量效率为目标的资源管理方案[7-10]. Liu等[7]为提高用户终端能效, 将其能量消耗转化为用户接收的符号数并求解. Gao等[8]考虑了基站拥有不完全信道状态信息时, 如何为用户分配资源使能量效率最大, 通过对中断概率和资源的约束建立优化问题, 并提出相应的求解算法. Kazemi等[9]考虑到最大能量效率的资源管理最优解求解复杂, 因此提出了一种低复杂度求解算法. Peng等[10]考虑了异构云无线接入网架构下通过合理分配无线资源来最大化能量效率.
云无线接入网将基带处理单元从基站解耦并组合为资源池, 并通过链路与远端射频单元相连, 集中式的资源管理和信号处理可以提高频谱效率和能量效率[10-13].但基带处理单元和射频单元的解耦使信号在链路中传输消耗时间, 且随着用户数量的增加而增加.上述文献中用户类型相同, 为满足不同用户需求, 仅对用户获得速率作出约束.而未来5G的用户数量不断增加且类型更加多样, 需求各有不同, 而频谱资源短缺, 因此需要更加灵活且满足不同类型用户需求的高频谱资源管理方案.
为了满足上述要求, 提供更加灵活的资源分配方案, 可通过分析不同业务场景下的用户需求, 并将其转化为对无线通信资源的需求.通过构建系统模型来求解最佳资源分配方案, 以系统总速率最大化为目标建立无线资源管理优化问题.由于其为混合整数非线性优化, 难以求解, 所以考虑了基于拉格朗日对偶理论和KKT条件对原优化的问题进行转化, 并对其迭代求解, 给出最优资源的分配算法.最后通过与已有算法对比, 并进行仿真分析, 验证了所提算法的有效性.
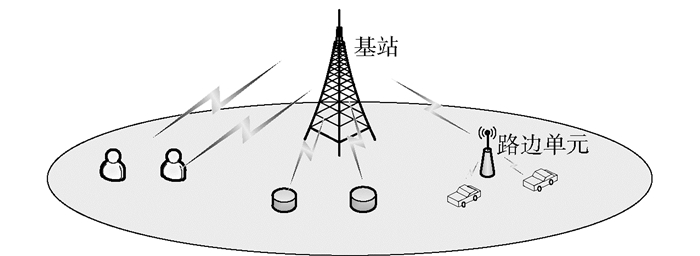
1 系统模型考虑如图 1所示的基于正交频分多址接入(OFDMA, orthogonal frequency division multiplexing access)系统的下行链路, 在基站覆盖范围内有属于不同NS的用户并为其提供通信服务.设NS集合为
|
图 1 系统模型 |
每类g∈
| $ {R_{{n_g},k}} = {x_{{n_g},k}}B{\rm{lb}}\left( {1 + \frac{{{p_{{n_g},k}}{{\left| {{h_{{n_g},k}}} \right|}^2}}}{{B{N_0}}}} \right) $ | (1) |
为简化起见, 令
用户ng的总速率为
| $ {R_{{n_g}}} = \sum\limits_{k \in \mathscr{K}} {{x_{{n_g},k}}} B{\rm{lb}}\left( {1 + {c_{{n_g},k}}{p_{{n_g},k}}} \right) $ | (2) |
前文已经分析过不同NS下的用户对性能要求差异较大, 也就是每个切片都有各自侧重点, 但同时也对其他性能指标要求有要求, 但是要求不高.因此需要分别对不同场景进行分析来满足其要求.
首先, G1切片下用户对速率要求较高, 得其传输速率约束为
| $ {R_{{n_g}}} \ge R_g^{{\rm{rsv}}},\forall {n_g} \in {\mathscr{N}_g},g \in {G_1} $ | (3) |
G1用户对可靠性要求虽然不高, 但需要满足一定的可靠性, 而可靠性的高低直接受误码率影响, 因此可转化为对误码率的约束.将可靠性约束转化为对误比特率(BER, bit error rate)r的约束为
| $ {r_{{n_g},k}} \le r_g^{{\rm{rsv}}},\;\;\;\forall {n_g} \in {\mathscr{N}_g},\;\;\;g \in {G_1} $ | (4) |
其次, G3切片下用户对时延及可靠性要求较高, 其中可靠性可以转化为误码率进行约束:
| $ {r_{{n_g},k}} \le r_g^{{\rm{rsv}}},\;\;\;\forall {n_g} \in {\mathscr{N}_g},\;\;\;g \in {G_3} $ | (5) |
对于传输数据量为sng的用户由于其在传输中消耗了部分时间, 假设已知当前剩余最大允许传输时延为tng, 对于时延要求可转化为对速率的要求:
| $ {R_{{n_g}}} \ge \frac{{{s_{{n_g}}}}}{{{t_{{n_g}}}}} = R_g^{{\rm{rsv}}},\forall {n_g} \in {\mathscr{N}_g},g \in {G_3} $ | (6) |
最后, 在G2切片中, 虽然用户密度较大, 但是在同一时刻大部分用户处于休眠状态并不需要传输数据, 只有少量用户需要传输数据且数据量较少.因此, 这里只关注需要进行传输数据的用户的要求, 即传输的速率和可靠性要求.得到其用户速率约束如下:
| $ {R_{{n_g}}} \ge R_g^{{\rm{rsv}}},\forall {n_g} \in {\mathscr{N}_g},g \in {G_2} $ | (7) |
可靠性约束转化为BER约束如下:
| $ {r_{{n_g},k}} \le r_g^{{\rm{rsv}}},\;\;\;\forall {n_g} \in {\mathscr{N}_g},\;\;\;g \in {G_2} $ | (8) |
设信号采用QPSK调制, 则传输信号的r与Eb/N0之间关系为
| $ r = \frac{1}{2}{\rm{erfc}}\left( {\sqrt {{E_{\rm{b}}}/{N_0}} } \right) $ | (9) |
其中余补误差函数erfc(x)为减函数:
| $ {\rm{erfc}}\left( x \right) = \frac{2}{{\sqrt {\rm{ \mathsf{ π} }} }}\int_x^\infty {{{\rm{e}}^{ - {\eta ^2}}}{\rm{d}}\eta } $ | (10) |
信噪比ε与Eb/N0之间关系为
| $ \frac{{{E_{\rm{b}}}}}{{{N_0}}} = \frac{\varepsilon }{{\left( {{R_{\rm{b}}}/B} \right)}} = \frac{{cp}}{{x{\rm{lb}}\left( {1 + cp} \right)}} $ | (11) |
则BER与信噪比ε的关系为
| $ r = \frac{1}{2}{\rm{erfc}}\left( {\sqrt {\frac{r}{{\left( {{R_{\rm{b}}}/B} \right)}}} } \right) = \frac{1}{2}{\rm{erfc}}\left( {\sqrt {\frac{{cp}}{{x{\rm{lb}}\left( {1 + cp} \right)}}} } \right) $ | (12) |
通过对上述系统模型的分析, 为提高频谱效率并保证用户的性能要求, 以最大化系统总速率为目标, 建立如下的优化问题:
| $ \begin{array}{l} \mathop {\max }\limits_{x,p} \sum\limits_{g \in \mathscr{G}} {\sum\limits_{{n_g} \in {\mathscr{N}_g}} {{\omega _g}{R_{{n_g}}}} } \\ {\rm{s}}.\;{\rm{t}}.\;\;{\rm{C1}}:\sum\limits_{g \in \mathscr{G}} {\sum\limits_{{n_g} \in {\mathscr{N}_g}} {{x_{{n_g},k}}} } \le 1,\forall k \in \mathscr{K}\\ \;\;\;\;\;\;{\rm{C}}2:{x_{{n_g},k}} \in \left\{ {0,1} \right\},\forall {n_g} \in {\mathscr{N}_g},\forall g \in \mathscr{G}\\ \;\;\;\;\;\;{\rm{C}}3:\sum\limits_{g \in \mathscr{G}} {\sum\limits_{{n_g} \in {\mathscr{N}_g}} {\sum\limits_{k \in \mathscr{K}} {{x_{{n_g},k}}{p_{{n_g},k}}} } } \le P\\ \;\;\;\;\;\;{\rm{C}}4:{r_{{n_g},k}} \le r_g^{{\rm{rsv}}},\forall {n_g} \in {\mathscr{N}_g},\forall g \in \mathscr{G},\forall k \in \mathscr{K}\\ \;\;\;\;\;\;{\rm{C}}5:{R_{{n_g}}} \ge R_g^{{\rm{rsv}}}\forall {n_g} \in {\mathscr{N}_g},\forall g \in \mathscr{G} \end{array} $ | (13) |
其中:ωg为不同切片用户加权系数; C1和C2为子信道的约束, 即每个子信道只能分配给一个用户; C3为分配给所有信道的功率总和, 必须小于基站的总功率; C4和C5则分别为误码率约束和速率约束.采用穷举搜索算法求解上述问题, 寻找到最优子信道分配方案需要NK次, 再通过注水法获得最优的功率分配, 整体算法复杂度为O(KNK), 可见, 当用户和信道规模较大时, 求解的复杂度相当大.
2 问题求解 2.1 问题转化下面根据得到的优化问题对其进行转化求解.令
| $ \begin{array}{*{20}{c}} {\overline {{\rm{C}}4} :\frac{{{c_{{n_g},k}}{p_{{n_g},k}}}}{{{\rm{lb}}\left( {1 + {c_{{n_g},k}}{p_{{n_g},k}}} \right)}} - \frac{{{x_{{n_g},k}}E_g^{{\rm{rsv}}}}}{{{N_0}}} \ge 0,}\\ {\forall {n_g} \in {\mathscr{N}_g},\forall g \in \mathscr{G}} \end{array} $ | (14) |
因此原问题转化如下:
| $ \begin{array}{*{20}{c}} {\mathop {\max }\limits_{x,p} \sum\limits_{g \in \mathscr{G}} {\sum\limits_{{n_g} \in {\mathscr{N}_g}} {\sum\limits_{k \in \mathscr{K}} {{\omega _g}} } } {R_{{n_g}}}}\\ {{\rm{s}}.\;{\rm{t}}.\;\;{\rm{C}}1,{\rm{C}}2,{\rm{C}}3,\overline {{\rm{C}}4} ,{\rm{C}}5} \end{array} $ | (15) |
Yu等[14]对多信道系统的非凸频谱优化问题进行了研究, 并提出了时间共享条件, 得出当信道数足够大时便满足此条件, 此时原问题的解和其对偶问题解之间的对偶差额为零, 实际中的信道数足够满足此条件, 因此可以通过求解对偶问题来获得原问题的解, 定义拉格朗日函数如下:
| $ \begin{array}{*{20}{c}} {L\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{p}},\alpha ,\mathit{\boldsymbol{\lambda }},\mathit{\boldsymbol{\mu }}} \right) = }\\ {\alpha \left( {P - \sum\limits_{g \in \mathscr{G}} {\sum\limits_{{n_g} \in {\mathscr{N}_g}} {\sum\limits_{k \in \mathscr{K}} {{x_{{n_g},k}}} } } {p_{{n_g},k}}} \right) + }\\ {\sum\limits_{g \in \mathscr{G}} {\sum\limits_{{n_g} \in {\mathscr{N}_g}} {{\omega _g}{R_{{n_g}}}} } + \sum\limits_{g \in \mathscr{G}} {\sum\limits_{{n_g} \in {\mathscr{N}_g}} {{\lambda _{{n_g}}}\left( {{R_{{n_g}}} - R_g^{{\rm{rsv}}}} \right)} } + }\\ {\sum\limits_{g \in \mathscr{G}} {\sum\limits_{{n_g} \in {\mathscr{N}_g}} {\sum\limits_{k \in \mathscr{K}} {{\mu _{{n_g}}}\left( {\frac{{{c_{{n_g},k}}{p_{{n_g},k}}}}{{\rm{lb}\left( {1 + {c_{{n_g},k}}{p_{{n_g},k}}} \right)}} - \frac{{{x_{{n_g},k}}E_g^{{\rm{rsv}}}}}{{{N_0}}}} \right)} } } = }\\ {\alpha P + \sum\limits_{g \in \mathscr{G}} {\sum\limits_{{n_g} \in {\mathscr{N}_g}} {\sum\limits_{k \in \mathscr{K}} {\left( {{\omega _g}{R_{{n_g},k}} - \alpha {x_{{n_g},k}}{p_{{n_g},k}} + {\lambda _{{n_g}}}{R_{{n_g},k}} - } \right.} } } }\\ {\left. {\frac{{{\mu _{{n_g}}}{x_{{n_g},k}}E_g^{{\rm{rsv}}}}}{{{N_0}}} + \frac{{{\mu _{{n_g}}}{c_{{n_g},k}}{p_{{n_g},k}}}}{{{\rm{lb}}\left( {1 + {c_{{n_g},k}}{p_{{n_g},k}}} \right)}}} \right) - }\\ {\sum\limits_{g \in \mathscr{G}} {\sum\limits_{{n_g} \in {\mathscr{N}_g}} {{\lambda _{{n_g}}}R_g^{{\rm{rsv}}}} } = }\\ {\sum\limits_{k \in \mathscr{K}} {{L_k}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{p}},\alpha ,\mathit{\boldsymbol{\lambda }},\mathit{\boldsymbol{\mu }}} \right)} + \alpha P - \sum\limits_{g \in \mathscr{G}} {\sum\limits_{{n_g} \in {\mathscr{N}_g}} {{\lambda _{{n_g}}}} } R_g^{{\rm{rsv}}}} \end{array} $ | (16) |
其中α、λ、μ为约束条件的拉格朗日乘子.通过拉格朗日乘子可以将一个具有复杂约束条件的问题转化为一个相对简单的无约束问题, 从而更容易获得问题的解, 并得到拉格朗日对偶函数为
| $ g\left( {\alpha ,\mathit{\boldsymbol{\lambda }},\mathit{\boldsymbol{\mu }}} \right) = \mathop {\max }\limits_{\mathit{\boldsymbol{x}},\mathit{\boldsymbol{p}}} L\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{p}},\alpha ,\mathit{\boldsymbol{\lambda }},\mathit{\boldsymbol{\mu }}} \right) $ | (17) |
对偶问题为
| $ \begin{array}{*{20}{c}} {\mathop {\max }\limits_{\alpha ,\mathit{\boldsymbol{\lambda }},\mathit{\boldsymbol{\mu }}} g\left( {\alpha ,\mathit{\boldsymbol{\lambda }},\mathit{\boldsymbol{\mu }}} \right)}\\ {{\rm{s}}.\;{\rm{t}}.\;\;\alpha \ge 0,\mathit{\boldsymbol{\lambda }} \ge 0,\mathit{\boldsymbol{\mu }} \ge 0} \end{array} $ | (18) |
通过观察可以将对偶问题分解成K个独立的子问题:
| $ \begin{array}{*{20}{c}} {{g_k}\left( {\alpha ,\mathit{\boldsymbol{\lambda }},\mathit{\boldsymbol{\mu }}} \right) = \mathop {\max }\limits_{\mathit{\boldsymbol{x}},\mathit{\boldsymbol{p}}} {L_k}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{p}},\alpha ,\mathit{\boldsymbol{\lambda }},\mathit{\boldsymbol{\mu }}} \right) = }\\ {\mathop {\max }\limits_{\mathit{\boldsymbol{x}},\mathit{\boldsymbol{p}}} \sum\limits_{g \in \mathscr{G}} {\sum\limits_{{n_g} \in {\mathscr{N}_g}} {\left( {{\omega _g}{R_{{n_g},k}} - \alpha {x_{{n_g},k}}{p_{{n_g},k}} + {\lambda _{{n_g}}}{R_{{n_g},k}} - } \right.} } }\\ {\frac{{{\mu _{{n_g}}}{x_{{n_g},k}}E_g^{{\rm{rsv}}}}}{{{N_0}}} + \frac{{{\mu _{{n_g}}}{c_{{n_g},k}}{p_{{n_g},k}}}}{{{\rm{lb}}\left( {1 + {c_{{n_g},k}}{p_{{n_g},k}}} \right)}}} \end{array} $ | (19) |
式(19)中令xng, k=1, 即假设子信道k分配给用户ng, 可得它为关于png, k的凹函数, 因此利用KKT条件对png, k求一阶导, 并令其为零, 可以得到每个用户的最优功率分配值, 得
| $ \begin{array}{*{20}{c}} {\frac{{\partial {L_k}}}{{\partial {p_{{n_g},k}}}} = \frac{{\left( {{\omega _g} + {\lambda _{{n_g}}}} \right)B{c_{{n_g},k}}}}{{\ln 2\left( {1 + {c_{{n_g},k}}{p_{{n_g},k}}} \right)}} - \alpha + \frac{{{\mu _{{n_g}}}{c_{{n_g},k}}}}{{{\rm{lb}}\left( {1 + {c_{{n_g},k}}{p_{{n_g},k}}} \right)}} - }\\ {\frac{{{\mu _{{n_g}}}}}{{{{\left( {{\rm{lb}}\left( {1 + {c_{{n_g},k}}{p_{{n_g},k}}} \right)} \right)}^2}}}\frac{{{p_{{n_g},k}}c_{{n_g},k}^2}}{{\ln 2\left( {1 + {c_{{n_g},k}}{p_{{n_g},k}}} \right)}}} \end{array} $ | (20) |
对
| $ \begin{array}{l} {Y_{{n_g},k}} = \frac{{\left( {{\omega _g} + {\lambda _{{n_g}}}} \right)B{c_{{n_g},k}}}}{{\ln 2\left( {1 + {c_{{n_g},k}}{p_{{n_g},k}}} \right)}} + \frac{{{\mu _{{n_g}}}{c_{{n_g},k}}}}{{ {\rm{lb}} \left( {1 + {c_{{n_g},k}}{p_{{n_g},k}}} \right)}} - \\ \frac{{{\mu _{{n_g}}}}}{{{{\left( { {\rm{lb}} \left( {1 + {c_{{n_g},k}}{p_{{n_g},k}}} \right)} \right)}^2}}}\frac{{{p_{{n_g},k}}c_{{n_g},k}^2}}{{\ln 2\left( {1 + {c_{{n_g},k}}{p_{{n_g},k}}} \right)}} \end{array} $ | (21) |
根据式(21)可知Yng, k为减函数, 当png, k=0时Yng, k为大于零的最大值, 当png, k→∞时Yng, k为趋于零的最小值.当最大值大于α时, 上述问题必有解; 当最大值小于α时, 则在定义域内无解并令png, k=0.
得到p*ng, k后, 将其值代入gk(α, λ, μ)中, 为了得到最优的子信道分配方案, 每个信道只能分配给一个用户, 需要选择最优的用户占用此信道, 其分配方案可以表示为
| $ x_{{n_g},k}^* = \left\{ {\begin{array}{*{20}{l}} {1,}&{{n_g} = \arg\;\max {H_{{n_g},k}}}\\ {0,}&{其他} \end{array}} \right. $ | (22) |
其中
| $ \begin{array}{*{20}{c}} {{H_{{n_g},k}} = \left( {{\omega _g} + {\lambda _{{n_g}}}} \right)B{\rm{lb}}\left( {1 + {c_{{n_g},k}}{p_{{n_g},k}}} \right) - \alpha {p_{{n_g},k}} + }\\ {{\mu _{{n_g}}}\left( {\frac{{{c_{{n_g},k}}{p_{{n_g},k}}}}{{{\rm{lb}} \left( {1 + {c_{{n_g},k}}{p_{{n_g},k}}} \right)}} - \frac{{E_g^{{\rm{rsv}}}}}{{{N_0}}}} \right)} \end{array} $ | (23) |
根据上面的分析可得每个子信道和功率的最优分配方案, 但当前的最优解不一定是全局最优解, 需要对拉格朗日乘子进行迭代更新.这里采用次梯度算法对拉格朗日乘子进行更新求解.
| $ \begin{array}{*{20}{c}} {\alpha \left( {t + 1} \right) = }\\ {{{\left[ {\alpha \left( t \right) - {\tau _\alpha }\left( t \right)\left( {P - \sum\limits_{g \in \mathscr{G}} {\sum\limits_{{n_g} \in {\mathscr{N}_g}} {\sum\limits_{k \in \mathscr{K}} {{x_{{n_g},k}}{p_{{n_g},k}}} } } } \right)} \right]}^ + }} \end{array} $ | (24) |
| $ {\lambda _{{n_g}}}\left( {t + 1} \right) = {\left[ {{\lambda _{{n_g}}}\left( t \right) - {\tau _\lambda }\left( t \right)\left( {{R_{{n_g}}} - R_g^{{\rm{rsv}}}} \right)} \right]^ + } $ | (25) |
| $ \begin{array}{*{20}{c}} {{\mu _{{n_g}}}\left( {t + 1} \right) = \left[ {{\mu _{{n_g}}}\left( t \right) - {\tau _\mu }\left( t \right) \times } \right.}\\ {{{\left. {\left( {\frac{{{c_{{n_g},k}}{p_{{n_g},k}}}}{{{\rm{lb}}\left( {1 + {c_{{n_g},k}}{p_{{n_g},k}}} \right)}} - \frac{{{x_{{n_g},k}}E_g^{{\rm{rsv}}}}}{{{N_0}}}} \right)} \right]}^ + }} \end{array} $ | (26) |
其中:
根据求解过程得到资源分配算法求解步骤如下:
1) 构造如式(16)的拉格朗日函数L(x, p, α, λ, μ), 并转化为对偶问题g(α, λ, μ);
2) 将g(α, λ, μ)分解为K个独立的子问题gk(α, λ, μ)并初始化拉格朗日乘子α0, λ0, μ0;
3) 根据式(21)和式(22)计算最优的信道分配和功率分配方案(x*, p*);
4) 根据信道及功率分配结果计算更新的g(α, λ, μ);
5) 根据次梯度算法更新拉格朗日乘子α, λ, μ;
6) 检查收敛条件是否满足, 若不满足则跳转到步骤3), 若满足收敛条件则结束循环并获得全局最优资源分配方案(x*, p*).
上述算法基于拉格朗日对偶理论, 并将对偶问题分解成K个独立的子问题, 每个子问题需要针对N个用户分别求解, 并经过有限次迭代后收敛到最优解, 可得该算法的计算复杂度为O(KN), 远远低于穷举搜索算法的复杂度, 大大降低了求解难度.
4 仿真结果为评价所提算法的资源分配性能, 下面对算法的性能进行仿真分析.由于不同类型用户性能要求差异较大, 同时为了比较所提算法获得的容量与系统所能达到最大容量, 选择了经典的比例公平算法(PF, proportional fairness)和最大容量算法(MAXR, maximum rate)进行比较.由于不同切片间性能要求差异化太大, 如在速率方面, eMBB切片要求的速率远远高于mMTC切片要求的速率, 如果直接用获得的速率大小来衡量公平性的话, 那么所有用户所得速率都趋于相等才能称之为公平, 为保证公平性则需要为mMTC切片分配更多的资源, 但是为mMTC切片分配超出它要求的速率是没有必要的, 同时也降低了其他用户获得的速率.因此认为采用比例公平更适合作为本文的公平度, 以衡量用户的公平性, 其公平度定义[15]为
| $ f = \frac{{{{\left( {\sum\limits_{g \in \mathscr{G}} {\sum\limits_{{n_g} \in {\mathscr{N}_g}} {\frac{{{R_{{n_g}}}}}{{R_g^{{\rm{rsv}}}}}} } } \right)}^2}}}{{N\sum\limits_{g \in \mathscr{G}} {\sum\limits_{{n_g} \in {\mathscr{N}_g}} {{{\left( {\frac{{{R_{{n_g}}}}}{{R_g^{{\rm{rsv}}}}}} \right)}^2}} } }} $ | (27) |
可看出
系统参数设置如下:设所有用户在基站覆盖半径为500米的范围内均匀分布, 系统总带宽为10 MHz, 利用OFDMA将其平均分成的子信道数为K=128, 系统总功率P为40 dBm.用户传输信道路径损耗和阴影衰落结合建模为38+30lgd+X, 单位为dB, 其中d表示基站与用户之间的距离, X单位为dB且为服从高斯分布的标准差为6 dB的阴影衰落随机变量. 3种切片的性能指标各不相同, 每个切片服务多个用户, 其中仿真中所用的切片用户数量的比例为2 :3 :5.不同的切片对应不同的权重系数ωg, 为仿真方便, 假设所有切片的权重系数均为1.当切片g∈G1时, 速率要求Rgrsv为1.5 Mbit/s, rgrsv为1×10-4; 当切片g∈G3时, 设其用户数据量为5 kbit, 剩余允许最大时延范围在5~10 ms之间, rgrsv为1×10-6; 当切片g∈G2时, 速率要求Rgrsv为0.3 Mbit/s, rgrsv为1×10-3.
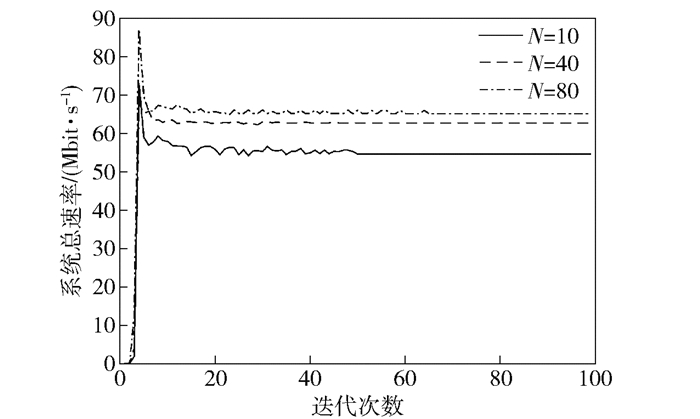
图 2所示为根据本文所提算法在不同总用户数的条件下, 系统总速率的收敛情况.随着总用户数量的增加, 算法迭代中求解的变量数量也会增加, 导致每次迭代复杂度有所提升, 而算法的收敛同时也受拉格朗日乘子迭代的影响, 导致不同对应收敛点是不同的, 但是从仿真中可以看出在迭代几十次后算法均达到收敛状态, 由此可以看出所提算法可以有效解决资源的分配问题.
|
图 2 系统总速率收敛情况 |
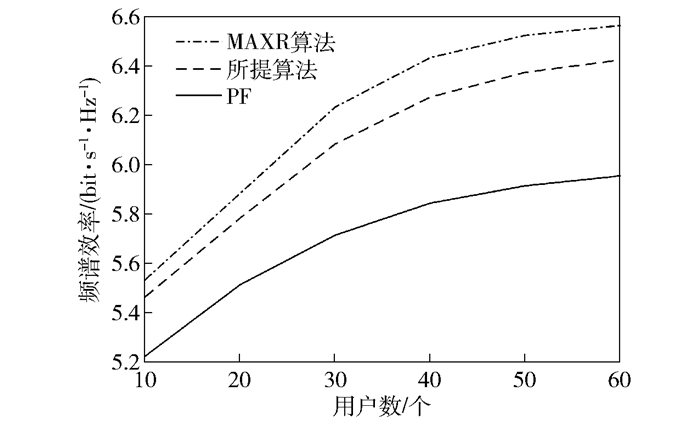
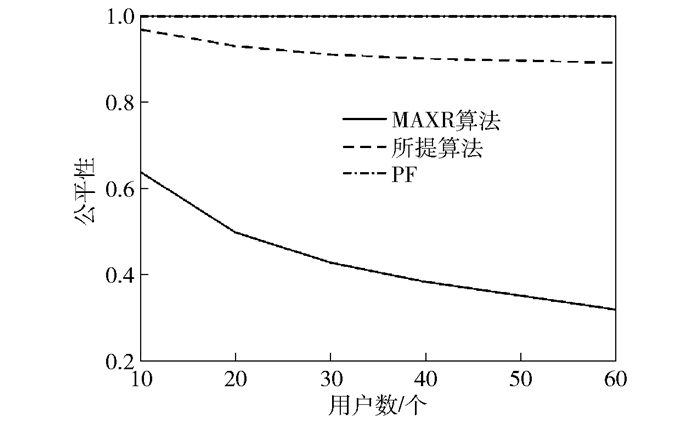
图 3是将所提算法与PF算法和MAXR算法的频谱效率对比仿真实验. 图 4是3种算法之间的公平性对比仿真实验.从中可以看出MAXR算法的频谱效率最大, 而用户公平性最差, 因为它将资源分配给信道条件最好的用户, 信道条件差的用户往往获取不到资源. PF算法则与MAXR算法正好相反, 因为它是按比例实现资源的分配.本文所提算法由于没有约束用户速率的比例公平性, 同时也保证信道条件差的用户也会获得资源, 因而在保证用户可以正常工作下充分利用信道增益, 实现系统总容量的最大化.从图 3可以看出其频谱效率只是略小于MAXR算法的频谱效率, 同时从图 4中看出保证了用户之间一定的公平性.因此, 可以总结出所提算法平衡了系统容量与用户之间的公平性, 实现了资源的合理分配, 并具有较好的性能.
|
图 3 所提算法与现有算法的系统容量对比 |
|
图 4 不同算法的公平性比较 |
为满足不同类型用户的差异化需求, 构建了基于NS的系统模型, 并以系统总速率最大为目标建立资源分配优化问题.为降低求解复杂度, 采用了拉格朗日对偶理论和KKT条件将问题进行转化求解, 并给出了最优资源分配算法.最后将所提算法与已有算法进行对比实验, 仿真结果证明了所提算法在保证一定用户公平性的前提下, 可以提高系统容量, 同时验证了算法的有效性.
| [1] |
ITU-R. IMT vision-framework and overall objectives of the future development of IMT for 2020 and beyond[S/OL].[2018-01-11]. https://www.itu.int/dmspubrec/itu-r/rec/m/R-REC-M.2083-0-201509-I!!PDF-E.pdf.
|
| [2] |
NGMN Alliance. 5G white paper[S/OL]. 2015[2018-03-11]. https://www.ngmn.org/fileadmin/ngmn/content/images/news/ngmn_news/NGMN_5G_White_Paper_V1_0.pdf.
|
| [3] |
3GPP. Study on architecture for next generation system: TR23.799[EB/OL]. 2016[2018-03-10]. https://www.3gpp.org/ftp/Specs/archive/23_series/23.799.
|
| [4] |
Parsaeefard S, Jumba V, Derakhshani M, et al. Joint resource provisioning and admission control in wireless virtualized networks[C]//IEEE Wireless Communications and Networking Conference. New Orleans: IEEE, 2015: 2020-2025.
|
| [5] |
Kamel M I, Long B L, Girard A. LTE wireless network virtualization: dynamic slicing via flexible scheduling[C]//IEEE Vehicular Technology Conference. Seoul: IEEE, 2014: 1-5.
|
| [6] |
Parsaeefard S, Dawadi R, Derakhshani M, et al. Joint user-association and resource allocation in virtualized wireless networks[J]. IEEE Access, 2016(4): 2738-2750. |
| [7] |
Liu J, Wang Y, Zhao Z, et al. Energy-efficient resource allocation in OFDMA-based wireless multicast systems[C]//IEEE International Conference on Advanced Communication Technology. PyeongChang: IEEE, 2017: 419-426.
|
| [8] |
Gao X, Yang K, Wu J, et al. Energy-efficient resource allocation and power control for downlink multi-cell OFDMA networks[C]//IEEE Global Communications Conference. Singapore: IEEE, 2017: 1-6.
|
| [9] |
Kazemi J, Omidi M J, Navaie K. A novel low complexity energy-efficient resource allocation for OFDM systems[J]. Transactions on Emerging Telecommunications Technologies, 2017, 28(1): 1-11. |
| [10] |
Peng M, Zhang K, Jiang J, et al. Energy-efficient resource assignment and power allocation in heterogeneous cloud radio access networks[J]. IEEE Transactions on Vehicular Technology, 2015, 64(11): 5275-5287. DOI:10.1109/TVT.2014.2379922 |
| [11] |
Stephen R G, Zhang R. Green OFDMA resource allocation in cache-enabled CRAN[C]//IEEE Online Conference on Green Communications Green Communications. Piscataway: IEEE, 2016: 70-75.
|
| [12] |
Dai B, Yu W. Energy efficiency of downlink transmission strategies for cloud radio access networks[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(4): 1037-1050. DOI:10.1109/JSAC.2016.2544459 |
| [13] |
Liu L, Bi S, Zhang R. Joint power control and fronthaul rate allocation for throughput maximization in OFDMA-based cloud radio access network[J]. IEEE Transactions on Communications, 2015, 63(11): 4097-4110. DOI:10.1109/TCOMM.2015.2469687 |
| [14] |
Yu W, Lui R. Dual methods for nonconvex spectrum optimization of multicarrier systems[J]. IEEE Transactions on Wireless Communications, 2006, 54(7): 1310-1322. DOI:10.1109/TCOMM.2006.877962 |
| [15] |
Jain R, Chiu D, Hawe W. A quantitative measure of fairness and discrimination for resource allocation in shared systems[R].[S.l.]: Digital Equipment Corporation, Technical Report TR-301, 1984.
|


