提出了一种基于加权混合滤波与重心法的近似三角形内点测试(APIT)改进定位算法(HFG-APIT).利用混合滤波过滤突变信号强度值使数据平滑稳定输出;再引入加权中位数来提高接收信号强度(RSSI)的精度;最后采用重心法进行内点测试减少误判,提高定位精度.仿真结果表明,混合滤波算法比其他滤波方法处理RSSI数据的测距精度更高,HFG-APIT的定位误差分别为最小二乘定位算法(LSM-RSSI)和APIT定位算法的41.7%和23.8%,整体定位性能也优于其他2种算法.
An improved approximate point-in-triangulation test (APIT) localization algorithm which based on weighted hybrid filtering and center of gravity method (HFG-APIT) was proposed. Hybrid filtering is used to filter abrupt signal strength values to make the data output smoothly and stably. Weighted median is then used to improve the accuracy of received signal strength indication (RSSI), the center of gravity method is used for interior point testing to reduce misjudgment and improve localization accuracy. Simulation results show that the hybrid filtering algorithm has higher ranging accuracy than other filtering methods in processing RSSI data and the localization errors of HFG-APIT are 41.7% and 23.8% of RSSI localization algorithm based on least squares method (LSM-RSSI) and APIT localization algorithm, the localization performance is also better than the other two algorithms.
利用无线传感器网络技术(WSN, wireless sensor network)对非煤矿山地压灾害进行监测,对于矿山地压预警、安全管理和事故救援有着极其重要的作用[1].在WSN中,定位算法主要分为基于测距和与距离无关的2种定位算法[2].基于信号接收强度(RSSI, received signal strength indication)的测距算法具有有效距离长,不需要额外硬件,成本低功耗小的优点,可以满足非煤矿山地压灾害监测对定位成本,定位能耗等方面的要求[3-4].
Wang C L[5]引入了高斯滤波(GF, Gaussian filtering)和卡尔曼滤波(KF, Kalman filtering)对信号强度RSSI进行滤波处理.但是在井下环境干扰较多的条件下,KF只能处理高噪音情况,不能有效地过滤突变数据[6];GF虽然对静止的目标数据输出稳定,但是当目标移动时相对误差会增大[7]. Wei Z等[8]提出了一种LSM-RSSI算法(LSM-RSSI, RSSI localization algorithm based on least square method),该算法在利用均值、中值和高斯混合滤波优化RSSI基础上采用最小二乘法的估算环境参数减少测量误差,但是单纯的改进计算式会增加计算误差,导致定位精度降低;Feng S等[9]提出了在近似三角形内点测试法(APIT, approximate point-in-triangulation test)基础上利用网格法找寻最大概率的质心坐标,该算法定位性能稳定但是利用面积法进行内点测试计算量大,判断时间长,耗能大[10-11].为此,提出一种基于加权混合滤波与重心法的APIT改进定位算法(HFG-APIT, APIT based on weighted hybrid filtering and center of Gravity method),利用GF和KF的混合滤波(HF, hybrid filtering)算法以及加权中位数对RSSI数据进行优化,再利用重心法对内点测试进行改进,以提高定位精度.
1 RSSI测距模型RSSI测距模型的核心思路是:根据接收到的信标节点和未知节点的信号强度计算得出信号在传播过程中的损耗,并以此建立符合实际环境的数学模型通过信号传播损耗计算出节点之间的距离,从而计算出未知节点的位置[12].通常使用对数—常态分布模型.对数—常态分布模型为
| $ P\left( d \right) = P\left( {{d_0}} \right) - 10n\lg \left( {\frac{d}{{{d_0}}}} \right) + {X_\sigma } $ | (1) |
其中:d为未知节点和信标节点之间的距离;P(d)表示无线信号经过距离d之后的信号强度;d0表示信标节点和参考节点之间的距离,通常取d0=1 m;P(d0)表示参考节点接收到的信号强度值;n表示路径衰减因子;Xσ是均值为0,方差为σ的正态分布随机变量,表示井下环境因素对无线信号的影响程度.
信号强度P(d)可以用RSSI值表示,将式(1)中的对数—常态分布模型式转换成含有RSSI值的形式,同时简化模型即忽略正态分布随机变量Xσ,得到
| $ {P_{{\rm{rssi}}}}\left( d \right) = {P_{{\rm{rssi}}}}\left( {{d_0}} \right) - 10n\lg \left( {\frac{d}{{{d_0}}}} \right) $ | (2) |
由式(2)可以得到未知节点和信标节点之间距离d的计算式为
| $ d = {d_0}{10^{\frac{{{P_{{\rm{rssi}}}}\left( {{d_0}} \right) - {P_{{\rm{rssi}}}}\left( d \right)}}{{10n}}}} $ | (3) |
由式(3)可以看出,未知节点和信标节点之间的距离不仅跟信标节点和参考节点之间的距离d0有关,还与路径衰减因子n有关.在不同的井巷以及不同的采场中,路径衰减因子n也不同,它是一个动态变化的参数.传统的理论模型建立在理想的抗干扰环境中,采用固定的路径衰减因子计算节点之间的距离会限制测距模型的精度,不能准确地反应未知节点的位置信息.为了降低测距误差可以通过利用滤波算法过滤异常的信号强度值,并根据外界环境的变化更新路径衰减因子[13].
2 HFG-APIT定位算法 2.1 卡尔曼滤波算法卡尔曼滤波算法的核心思路是通过无线传感器节点获取当前时刻的RSSI测量值,然后由当前时刻的RSSI测量值和上一时刻的最优预测值计算出当前时刻的最优预测值.这是一种线性递归数据处理的优化算法.该算法主要有预测和更新2个阶段.首先在预测阶段中,t时刻状态预测为
| $ X\left( {t|t - 1} \right) = \mathit{\boldsymbol{F}}X\left( {t - 1|t - 1} \right) + \mathit{\boldsymbol{G}}U\left( t \right) $ | (4) |
t时刻协方差预测为
| $ P\left( {t|t - 1} \right) = \mathit{\boldsymbol{F}}P\left( {t - 1|t - 1} \right){\mathit{\boldsymbol{F}}^{\rm{T}}} + Q $ | (5) |
其中:X(t|t-1)为t-1时刻的RSSI预测值;F和G为系统参数,因为RSSI值就是测量所得到的值,所以系统参数在这里都取1;X(t-1|t-1)为t-1时刻RSSI的最优值,同时也是t时刻的系统预测值;U(t)为控制参数,在这里取0;P(t|t-1)为X(t|t-1)对应的协方差;P(t-1|t-1)为X(t-1|t-1)对应的协方差;Q表示均值为0的高斯过程噪声协方差.
在更新阶段中,t时刻状态更新为
| $ X(t|t) = X(t|t - 1) + [Y(t) - X(t|t - 1)]{T_g}(t) $ | (6) |
t时刻协方差更新为
| $ P(t|t) = \left[ {\mathit{\boldsymbol{I}} - {T_g}(t)H} \right]P(t|t - 1) $ | (7) |
Tg(t)为t时刻卡尔曼增益,计算式为
| $ {T_g}(t) = \frac{{P(t|t - 1)}}{{P(t|t - 1) + H}} $ | (8) |
其中:X(t|t)为t时刻RSSI的最优值, Y(t)为t时刻RSSI的测量值, H为测量到的噪声协方差, P(t|t)为t时刻的RSSI的最优值对应的协方差, I为单位矩阵,I=1.
卡尔曼滤波不需要储存每一次的测量信息,并且可以实时处理得到的观测信息.但是当RSSI值受非煤矿山井下复杂环境因素影响发生突变时,卡尔曼滤波算法不能有效地消除突变数据带来的影响,导致数据整体产生较大的波动.
2.2 高斯滤波算法高斯滤波算法的核心思路是通过建立高斯模型来预设合适的高概率发生区域.区域内的RSSI值即为节点接收到的有效RSSI值,将这组RSSI值进行算术平均后作为有效数据参与下一步的定位.在该高概率发生区域之外的RSSI值为无效数据,这些无效数据大多是因为无线信号受到外界环境因素干扰而形成的需要剔除的突变数据.将这些无效数据剔除后可以得到更准确的RSSI值参与下一步的定位.设未知节点接收到n个RSSI值样本数据分别是R1, R2, …, Rn,对应的概率分布为P1, P2, …, Pn.
RSSI服从(μ, σ)的高斯分布,其概率密度函数为
| $ F(R) = \frac{1}{{\sigma \sqrt {2{\rm{ \mathtt{ π} }}} }}{{\rm{e}}^{\frac{{ - {{(R - \mu )}^2}}}{{2{\sigma ^2}}}}} $ | (9) |
其中R为RSSI值,由极大似然估计法可以求得:
| $ \mu = \frac{1}{n}\sum\limits_{i = 1}^n {{R_i}} $ | (10) |
| $ \sigma = \sqrt {\frac{1}{{n - 1}}\sum\limits_{i = 1}^n {{{\left( {{R_i} - \mu } \right)}^2}} } $ | (11) |
函数F(R)在区间(μ-σ≤Ri≤μ+σ)的概率为
| $ \begin{array}{*{20}{c}} {P\left( {\mu - \sigma \le {R_i} \le \mu + \sigma } \right) = F(\mu + \sigma ) - F(\mu - \sigma ) = }\\ {\phi (1) - \phi ( - 1) = 2\phi (1) - 1 = 0.6826} \end{array} $ | (12) |
函数F(R)为高斯分布函数高概率发生区,过滤数值时只保留发生在这个区域内的R值为有效值,求出其算术平均值为
| $ \bar R = \frac{1}{n}\sum\limits_{i = 1}^n {{R_i}} , \;\;\;{R_i} \in (\mu - \sigma , \mu + \sigma ) $ | (13) |
高斯滤波算法通过建立高斯模型去掉测量时的突变数据,没有将其纳入计算中,消除了突变数据对测量结果的影响,能得到更加符合非煤矿山井下环境的RSSI值,从而使未知节点和信标节点之间的距离更加精确.但是高斯滤波算法收集的测量数据多,测量时间较长,当未知节点发生位移时,测量误差会增大.
2.3 混合滤波算法为了提高滤波算法的精度,不仅要有效消除突变数据带来的影响,还应该保持测量数据整体平滑的输出,于是在高斯滤波算法和卡尔曼滤波算法基础上,引入加权中位数处理RSSI数据.
利用加权中位数处理RSSI数据首先需要从RSSI序列中找出中位数MR.设未知节点接收到n个RSSI值样本数据分别是R1, R2, …, Rn,将RSSI数据按数值大小进行排序:R1≤R2≤…≤Rn,序列的中位数为
| $ {M_R} = \left\{ \begin{array}{l} {R_{\frac{{n + 1}}{2}}}, \;\;\;\;\;n\;是奇数\\ \frac{1}{2}\left( {{R_{\frac{n}{2}}} + {R_{\frac{{n + 1}}{2}}}} \right), \;\;\;\;\;n\;是偶数 \end{array} \right. $ | (14) |
求出序列中RSSI值与MR的方差为
| $ {D_i} = {\left( {{R_i} - {M_R}} \right)^2} $ | (15) |
其中:Ri为序列中第i个RSSI数据的值,Di为其对应的方差.但是当Ri=MR时,Di=0,式(15)没有意义,因此引入加权系数处理式:
| $ {\omega _i} = \frac{1}{{1 + {D_i}}} $ | (16) |
将加权系数累加后进行归一化处理得到加权权重Wi.
| $ {W_i} = \frac{{{\omega _i}}}{{\sum\limits_{i = 1}^n {{\omega _i}} }} $ | (17) |
将序列中的每一个RSSI值与加权权重Wi相乘后累加得出两节点之间的RSSI数据.
| $ R = \sum\limits_{i = 1}^n {\left( {{W_i}{R_i}} \right)} $ | (18) |
混合滤波算法的核心思路是:利用高斯滤波算法对收集到的RSSI数据进行过滤,过滤掉高概率发生区外的RSSI数据后,利用卡尔曼滤波算法对高概率发生区内的RSSI数据进行迭代,最后利用加权中位数处理RSSI数据,得到节点之间的信号强度值,提高RSSI精度.算法流程如图 1所示.

|
图 1 混合滤波算法流程 |
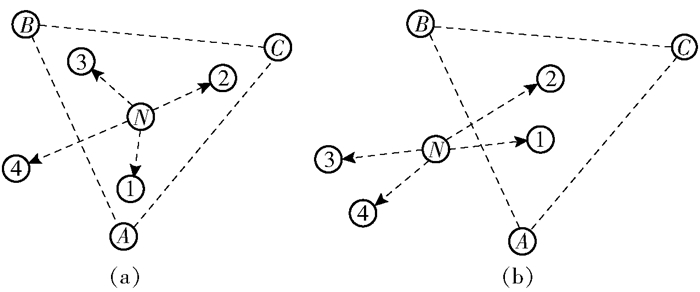
APIT算法是一种以最佳三角形内点测试算法(PIT, perfect point-in-triangulation test)为基础的自主非测距定位算法.在非煤矿山地压灾害监测中,节点大部分处于静止状态.所以APIT算法的核心思路是:节点N的所有邻居节点中存在一节点M,当节点N沿着某一方向朝节点M移动时,满足同时靠近或者远离3个信标节点A、B、C的情况,那么节点N在三角形ABC外部;否则,节点N在三角形ABC内部.
传统的APIT定位算法在节点密度高的情况下定位精度也更高,但是在非煤矿山地压灾害监测中,由于节点密度较低会导致定位精度降低,其主要原因是容易发生外判内(out-to-in)或者内判外(in-to-out)的误判,如图 2所示.
|
图 2 APIT算法误判原理 |
笔者提出一种基于重心法的内点测试法,该算法的思路是:三角形3个顶点按顺时针排列顺序是A、B、C.选择顶点A为起点,那么点B相当于点A沿AB方向移动一定距离得到,点C相当于点A沿AC方向移动一定距离得到.对于平面内任意一点N,由重心规律可得
| $ N - a = u(c - a) + v(b - a) $ | (19) |
其中:u、v分别为边长AC、AB的系数,a、b、c分别表示点A、B、C.如果系数为负值,则表示点A是沿BA、BC方向移动.若点N同时满足以下条件则表示其在三角形ABC的内部:
| $ \left. {\begin{array}{*{20}{l}} {\mu \ge 0}\\ {\nu \le 0}\\ {\mu + \nu = 1} \end{array}} \right\} $ | (20) |
当u=v=0时,就是点A;当u=0,v=1时,就是点B;当u=1,v=0时,就是点C.令S0=N-a,S1=c-a,S2=b-a代入式(19):
| $ {S_0} = u{S_1} + v{S_2} $ | (21) |
由于一个方程并不能解出系数u、v,所以将式(21)等号两边同时点乘S1和S2得到方程组(22):
| $ \left. {\begin{array}{*{20}{l}} {{S_0}{S_1} = u\left( {{S_1}{S_1}} \right) + v\left( {{S_2}{S_1}} \right)}\\ {{S_0}{S_2} = u\left( {{S_1}{S_2}} \right) + v\left( {{S_2}{S_2}} \right)} \end{array}} \right\} $ | (22) |
解得
| $ \left. \begin{array}{l} u = \frac{{\left( {{S_2}{S_2}} \right)\left( {{S_0}{S_1}} \right) - \left( {{S_2}{S_1}} \right)\left( {{S_0}{S_2}} \right)}}{{\left( {{S_1}{S_1}} \right)\left( {{S_2}{S_2}} \right) - \left( {{S_1}{S_2}} \right)\left( {{S_2}{S_1}} \right)}}\\ v = \frac{{\left( {{S_1}{S_1}} \right)\left( {{S_0}{S_2}} \right) - \left( {{S_1}{S_2}} \right)\left( {{S_0}{S_1}} \right)}}{{\left( {{S_1}{S_1}} \right)\left( {{S_2}{S_2}} \right) - \left( {{S_1}{S_2}} \right)\left( {{S_2}{S_1}} \right)}} \end{array} \right\} $ | (23) |
将解出的u、v代入式(20)即可判断点N是否在三角形ABC的内部.利用重心法改进的APIT算法其最大优势是计算速度更快,并且避免了发生外判内(out-to-in)或者内判外(in-to-out)的误判.
2.5 算法步骤APIT核心算法步骤如下:
步骤1 信标节点周期性的向邻居节点发射自身相关信息.如坐标、ID、信号强度初值等.
步骤2 未知节点收集通讯范围内所有信标节点的位置信息.假设未知节点接收到n个信标节点信息,若n≥3,执行下一步;否则,结束定位.
步骤3 从n个信标节点中任意选择3个节点组成三角形,共Cn3个.利用滤波算法得出的RSSI值和信标节点坐标信息代入式(20)、式(23),判断未知节点是否在三角形内.
步骤4 筛选出所有包含未知节点的三角形,并求得重叠区域质心位置信息,即未知节点的位置信息.
步骤5 输出未知节点位置信息,完成节点定位.
3 仿真结果与分析为验证HFG-APIT算法的有效性,利用Matlab2018-b分别对滤波算法以及定位算法进行仿真分析.
3.1 滤波算法仿真通过滤波算法仿真,分别模拟HF、GF、KF在非煤矿山深井环境下的优化性能. 图 3所示为测距误差对比,测量距离为25 m,每隔0.5 m测一组,每组数据测100次求均值.由图 3可以看出,HF滤波算法平均测距误差为0.4 m,分别是KF、GF滤波算法平均测距误差的30.8%和21.1%.说明HF滤波算法对非煤矿山井下节点定位有较高的定位精度和较好的优化性能,并且数据输出稳定,波动较少.

|
图 3 测距误差对比 |
选用归一化平均定位误差Er作为评价标准为
| $ {E_r} = \frac{1}{K}\sum\limits_{i = 1}^K {\sqrt {{{\left( {{x_n} - {{\hat x}_n}} \right)}^2} + {{\left( {{y_n} - {{\hat y}_n}} \right)}^2}} } $ | (24) |
其中:K为节点总数, (xn, yn)为节点n的真实坐标,
仿真环境拓扑结构由区域内的信标节点生成,假设仿真区域是一个10 m×200 m的二维矩形区域.信标节点20个,由人工布置在巷道两侧,未知节点100个,假设信标节点的通信半径为50 m,仿真100次.空间信号损失模型采用对数—常态分布模型,其中路径衰减因子取4.0,信标节点和目标节点之间的距离d0=1 m时的RSSI值为45.
图 4为HFG-APIT算法与APIT、LSM-RSSI算法定位误差对比图.从图 4可以看出,HFG-APIT算法的定位误差在0.3~0.6 m,LSM-RSSI算法的定位误差在1.2~1.7 m,APIT算法的定位误差在2.2~3.7 m,HFG-APIT算法的平均定位误差为0.5 m,是LSM-RSSI算法(平均误差1.2 m)的41.7%,APIT(平均误差2.1 m)定位算法的23.8%.

|
图 4 定位误差对比 |
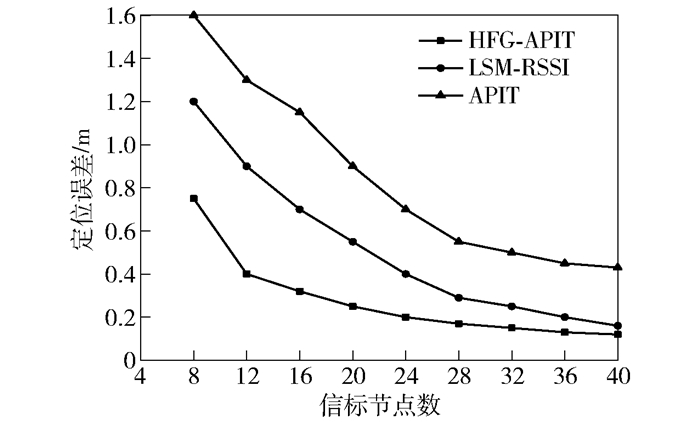
在仿真区域随机布置150个节点,通信半径为50 m,其中信标节点数量分别为8、12、16、20、24、28、32、36、40. 图 5所示为3种算法在信标节点数量改变时的定位误差对比.可以看出,3种算法的定位误差在总趋势上随着信标节点数量增加而减小. HFG-APIT算法在不同信标节点数量条件下都优于其余2种算法,并且当信标节点数量大于16时,HFG-APIT定位误差最先趋于稳定. HFG-APIT定位算法的平均定位误差为0.28 m,分别是LSM-RSSI和APIT定位算法的53.5%和32.8%.
|
图 5 不同信标节点数量定位误差对比 |
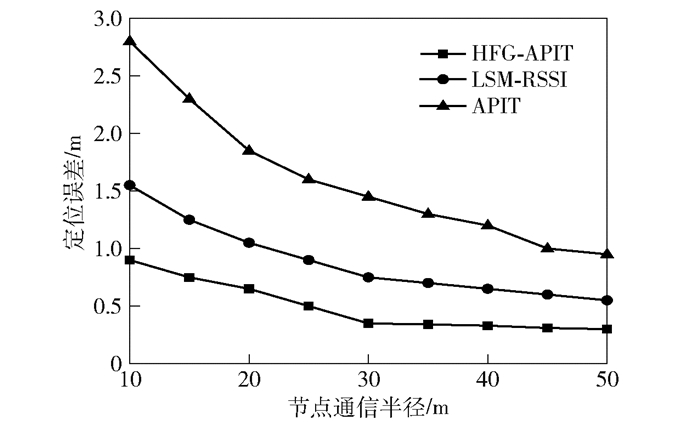
仿真区域随机布置150个节点,通信半径为10~50 m,其中信标节点数量为20个. 图 6所示为3种算法通信半径改变时的定位误差对比.可以看出,3种算法的定位误差在总趋势上随着通信半径的增大而减小,并且HFG-APIT算法在不同的通信半径条件下都优于其余2种算法. HFG-APIT定位算法的平均定位误差为0.49 m,分别是LSM-RSSI和APIT定位算法的55.4%和30.7%.
|
图 6 不同通信半径下的定位误差对比 |
仿真区域布置20个信标节点,通信半径为50 m,总节点数分别为80、100、120、140、160、180、200、220个. 图 7所示为3种算法总节点数改变时的定位误差对比.可以看出,3种算法的定位误差在总趋势上随着总节点数的增加而减小,并且随着节点的总数增多越趋于稳定. HFG-APIT算法在不同总节点数的情况下都优于其余2种算法. HFG-APIT定位算法的平均定位误差为0.29 m,分别是LSM-RSSI和APIT定位算法的54.2%和29.4%.

|
图 7 不同总节点数定位误差对比 |
非煤矿山井下环境容易导致节点接收到的RSSI值发生突变以及APIT算法易出现out-to-in或者in-to-out的误判问题,对此,提出一种基于加权混合滤波算法和重心法的HFG-APIT定位算法.在高斯滤波和卡尔曼滤波算法的基础上引入加权中位数处理信号强度值,实现数据精确输出.利用重心法进行未知节点的内点测试,有效减少了误判,进一步提高了定位精度.仿真结果表明,经HF滤波处理后的RSSI测距精度要高于GF滤波和KF滤波;HFG-APIT定位算法精度也高于LSM-RSSI算法和APIT算法.
| [1] |
余修武, 刘琴, 李向阳, 等. 基于改进蚁群的BP神经网络WSN数据融合算法[J]. 北京邮电大学学报, 2018, 41(4): 91-96. Yu Xiuwu, Liu Qin, Li Xiangyang, et al. Information fusion algorithm based on improved ant colony optimization BP neural network in WSN[J]. Journal of Beijing University of Posts and Telecommunications, 2018, 41(4): 91-96. |
| [2] |
Cheng Jiulong, Song Guangdong, Liu Tongyu, et al. High precision location of micro-seismic source in underground coal mine[J]. Chinese Journal of Geophysics, 2016, 59(6): 734-743. DOI:10.1002/cjg2.30021 |
| [3] |
Li G, Geng E, Ye Z, et al. Indoor positioning algorithm based on the improved RSSI distance model[J]. Sensors, 2018, 18(9): 2820-2835. DOI:10.3390/s18092820 |
| [4] |
Cheikhrouhou O, Bhatti G M, Alroobaea R. A hybrid DV-Hop algorithm using RSSI for localization in large-scale wireless sensor networks[J]. Sensors, 2018, 18(5): 1469-1483. DOI:10.3390/s18051469 |
| [5] |
Wang C L. Decentralized target positioning and tracking based on a weighted extended kalman filter for wireless sensor networks[J]. Wireless Networks, 2013, 19(8): 1915-1931. DOI:10.1007/s11276-013-0573-1 |
| [6] |
Fang X, Jiang Z, Nan L, et al. Noise-aware localization algorithms for wireless sensor networks based on multidimensional scaling and adaptive Kalman filtering[J]. Computer Communications, 2016, 101(5): 57-68. |
| [7] |
Tseng C H, Yen J S. Enhanced gaussian mixture model of RSSI purification for indoor positioning[J]. Journal of Systems Architecture, 2017, 81(4): 1-6. |
| [8] |
Wei Z, Chen X, Huang Y, et al. A distance measurement algorithm based on hybrid filter and nodes adaptive correction model[J]. Chinese Journal of Sensors and Actuators, 2016, 29(8): 1280-1283. |
| [9] |
Feng S, Wu C D, Zhang Y Z. Dynamic localization of mobile robot based on improved APIT[J]. Journal of Beijing University of Posts and Telecommunications, 2016, 39(05): 67-71, 88. |
| [10] |
Liu J, Wang Z, Yao M, et al. VN-APIT:virtual nodes-based range-free APIT localization scheme for WSN[J]. Wireless Networks, 2016, 22(3): 1-12. |
| [11] |
Lasla N, Younis M F, Ouadjaout A, et al. An effective area-based localization algorithm for wireless networks[J]. IEEE Transactions on Computers, 2015, 64(8): 2103-2118. DOI:10.1109/TC.2014.2366744 |
| [12] |
Yaghoubi F, Abbasfar A A, Maham B. Energy efficient RSSI-based localization for wireless sensor networks[J]. IEEE Communications Letters, 2014, 18(6): 973-976. DOI:10.1109/LCOMM.2014.2320939 |
| [13] |
Tateishi, Kazuya, Ikegami, et al. Estimation method of attenuation constant during localization in RSSI[J]. International Journal of Radiation Oncology Biology Physics, 2015, 91(5): 1026-1033. DOI:10.1016/j.ijrobp.2014.12.043 |


