对于由各向同性偶极子天线组成的均匀圆阵(UCA, uniform circular array)而言，单元天线的相位中心^[1-2]位于其几何中心，它们可视作理想点源，相位中心偏移^[2]对来波信号的波达方向(DOA, direction of arrival)估计的影响不予考虑.如果组成圆阵的单元天线是非各向同性的，如考虑到短波交叉极化信号的DOA估计问题而设计的内向型水平极化对数周期天线测向圆阵、为满足高频信号固定来波指向的高增益接收而架设的外向型角锥喇叭天线测向圆阵等，按照常规的理想点源建立的阵列信号模型来解决天线间互耦、阵列校准^[3]以及相干信号DOA估计等问题显然是不合适的.这是因为单元天线的非各向同性导致阵列天线的相位中心并不在其几何中心，甚至并不存在一个固定唯一的相位中心，而且相位中心与入射信号的频率、极化、来波方向以及天线类型有关^[1].近些年来的研究，如基于相位效率计算的环形天线的相位中心估计模型研究^[4]、极化探测天线相位中心的测量^[5]、根据抛物面天线在远场观察点处的场强分布计算相位中心的二阶导数法、针对角锥喇叭的边缘衍射法和三元法，在微波暗室内对微带天线的辐射方向图进行采样或者对相位中心校准^[6]，运用最大似然方法计算天线的平均电场相位中心等，都是在具体天线类型或特定应用场景下对相位中心进行求解计算的.由于定向性天线相位中心的不确定性引起天线阵列有效孔径的变化，如果以天线阵列的几何中心作为参考点对来波信号进行DOA估计，随之产生的相位中心偏移对信号来波的DOA估计精度有很大影响，甚至导致波达角的错误估计.

在相同的辐射功率下，定向性天线接收的信号比全向性天线具有更低的峰值旁瓣比、更强的方向性指向，它的DOA估计模型有别于全向性天线阵列，目前的研究主要集中在天线方向图、阵列优化、方向性系数等因素上.例如，通过控制定向性天线主波瓣指向设计双传感器测向系统^[7]；研究均匀同心圆阵在期望方向上虚拟UCA的DOA估计问题^[8]；研究定向性天线阵列DOA估计与算法的依赖性及其与主波瓣位置之间的关系^[9]；通过优化单元天线方向图来设计定向性均匀线阵，从而对目标空域内潜在入射方向上的信号进行DOA估计性能的研究^[10]；通过优化方向性系数设计接近理论增益的微带天线阵列，与偶极子天线组成的全向天线阵列进行DOA估计比较，并对用于DOA估计的UCA带宽进行研究^[11].而笔者的主要工作是对引起定向性天线阵列DOA估计误差甚至错误的影响因素进行研究；同时综合考虑相位扰动、相位中心估计误差等因素对DOA估计精度的影响，分析这些误差因素并推导其误差矢量；对传统理想点源的DOA估计模型进行改进，建立一个基于相位中心的扇区DOA估计模型.通过实验仿真对影响DOA估计误差的因素进行研究，验证新模型的正确性和有效性.

1 阵列天线的相位中心

定向性天线远场区的波前相位并不是等相位球面，不过可以找到一个与天线关联的点的位置，使得如果将其作为一个沿着孔径延伸到远场区观测点的球面的球心，则辐射场分量在辐射球体表面上的相位基本是恒定的，至少在天线主波瓣内的相位值不随观测角度变化而变化，这个与天线相关联的点就是天线的相位中心或视在相位中心.

1.1 远场区场强分布

由2N+1个单元天线组成的均匀测向圆阵中第l个单元天线在远场区某观测点d_l处的辐射场强矢量E_l可表示为

$ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{E}}_l} = {I_l}{{\rm{e}}^{{\rm{j}}\phi \left( l \right)}}{G_l}\left( {\theta , \varphi } \right)\frac{{{{\rm{e}}^{ - {\rm{j}}k{d_l}}}}}{{{d_l}}}\mathit{\boldsymbol{u}}}\\ {{\rm{s}}.\;{\rm{t}}.\;\;{d_l} \gg 2{D^2}/\lambda } \end{array} $

(1)

其中：θ和φ分别为辐射信号的俯仰角度和方位角度；j= $ \sqrt { - 1} $为虚数单位；I_le^jϕ(l)为第l个单元天线的激励电流，I_l和ϕ(l)分别为激励电流的幅度和相位；G_l(θ, φ)为第l个单元天线的功率方向图；d_l为单元天线到观测点的远场距离；k为波数，k=2π/λ；λ为波长；u为单位极化矢量；D为阵列(有效)孔径，与单元天线的方向特性以及阵列结构有关，如由超宽频带对数周期天线组成的UCA，它的阵列孔径是随着频率的变化而变化的.天线阵列在远场观测点处总的辐射场强E_sum表示为

$ {E_{{\rm{sum}}}} = \sum\limits_{l = - N}^N {\left( {{\mathit{\boldsymbol{E}}_l}{\mathit{\boldsymbol{C}}_l}} \right)f} $

(2)

其中：C_l为单元天线l与其他单元天线之间的耦合系数矢量；f为阵列因子，它是一个与辐射角度有关的变量，可表示为

$ f = \sum\limits_{l = - N}^N {\exp } \left( { - {\rm{j}}kR\left( {\mathit{\boldsymbol{e}}{\mathit{\boldsymbol{p}}_l}} \right)} \right) $

(3)

其中：e=(sin θcos ϕ, sin θsin ϕ, cos θ)是辐射角的单位矢量，p_l=(x_l, y_l, z_l)为第l个单元天线相位中心的位置坐标，R的取值是阵列(有效)孔径D的一半.假设阵列中各个单元天线的激励电流是等幅同相的，即I_l=I，ϕ(l)=ϕ；各单元天线相同且功率方向图近似不变，即G_l(θ, φ)=G(θ, φ)；所有单元天线的主极化分量一致；单元天线间的耦合影响可以折算到单元激励上，或者将其视为天线方向图上的扰动予以考虑，这里暂不考虑单元天线间的耦合影响，即耦合系数矩阵为单位矩阵.那么，对于远场区观测点d_l≫R的电场辐射，如果令d_l≈d，式(2)就表示为

$ \begin{array}{*{20}{c}} {{E_{{\rm{sum}}}} = G\left( {\theta , \varphi } \right)\frac{I}{d}\sum\limits_{l = - N}^N {\exp } \left( { - {\rm{j}}kR\left( {\mathit{\boldsymbol{e}}{\mathit{\boldsymbol{p}}_l} - d} \right) + \phi } \right) \buildrel \Delta \over = }\\ {\left| {E\left( {\theta , \varphi } \right)} \right|{{\rm{e}}^{{\rm{j}}\mathit{\Psi }\left( {\left( {\theta , \varphi } \right), \lambda } \right)}}} \end{array} $

(4)

其中：E(θ, φ)是电场在远场区观测点d处的幅度；Ψ((θ, φ), λ)=$ \sum\limits_l$ exp (－j2πR(ep_l－d)+ϕ)/λ)是电场在远场区观测点d处的相位，它是一个与辐射角度和波长λ有关的电场分量.

1.2 相位中心的估计

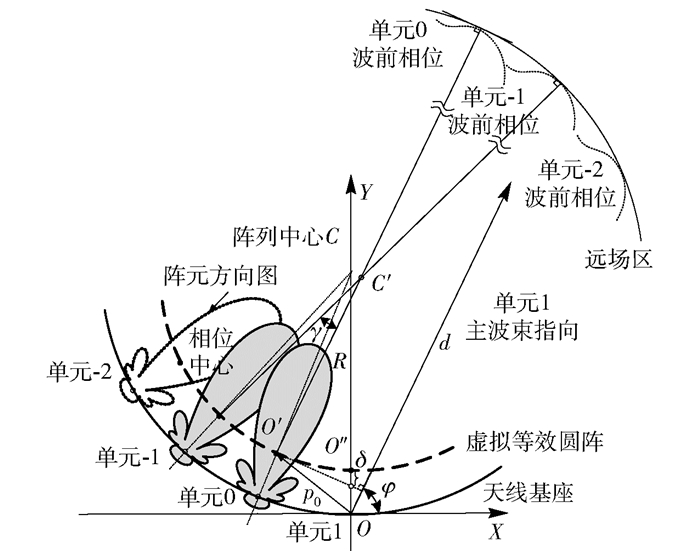
以超宽带非频变对数周期偶极子天线阵列为例，给出由定向天线组成的内向型UCA的相位中心估计模型，如图 1所示.

该阵列中各个单元天线的虚顶点都交于圆阵中心，并且各个单元天线的阵元面平行于纸面，这样单元方向图就是其E面内的方向图.为了简化推导，这里仅描述θ=π/2时辐射场在E面上的等相线分布情况，并假设各个单元天线在远场区的相位在主波瓣宽度内服从均匀分布.在这里只关心单元天线在主波瓣范围内的相位方向图以及它们的相位中心在阵列中的相对位置.单元天线主波瓣内的辐射角度须满足以下关系：

$ \begin{array}{*{20}{c}} {{{\left. {\left( {\theta , \varphi } \right)} \right|}_{\theta = {\rm{ \mathtt{ π} }}/2}} \in \left\{ {\left( {\alpha , \beta } \right)\left| {G\left( {\alpha , \beta } \right) > 1 - \left| {{E_{2{\theta _{0, 5}}}}} \right|/\left| {{E_{\max }}} \right|} \right.} \right.}\\ {\left. {{\rm{s}}{\rm{.}}\;{\rm{t}}{\rm{. }}\;0 \le \alpha \le \theta , 0 \le \beta \le 2{\rm{ \mathtt{ π} }}} \right\}} \end{array} $

(5)

其中：G(α, β)是单元天线的功率方向图函数，E_max和E_2θ0.5分别是单元天线在主波瓣范围内最大辐射方向上的辐射场强和半功率波瓣宽度处的辐射场强.根据单元天线1和单元天线0之间的位置关系以及二者在主波瓣指向φ上的波程差，可以得到远场区单元天线1和单元天线0之间的相位关系：

$ {\mathit{\Psi }_1}\left( {\left( {{\rm{ \mathtt{ π} }}/2, \varphi } \right), \lambda } \right) = {\mathit{\Psi }_0}\left( {\left( {{\rm{ \mathtt{ π} }}/2, \varphi } \right), \lambda } \right) + k\delta \sin \varphi $

(6)

其中δ=‖p₀‖sinφ－‖p₁‖cos φ. p₀是单元天线0相位中心的位置矢量，p₀=(x₀, y₀, 0)；p₁是单元天线1相位中心的位置矢量，p₁=(x₁, y₁, 0).在主波瓣范围内，单元天线在远场区观测点处的相位为一常数c.不过实际情况并非如此，由于天线制造工艺、安装误差及阵间耦合等因素影响，单元天线在主波瓣宽度内的远场相位并不在一个等相球面上，已不再是常数，而是在一定范围存在相位扰动ξ.因此，可以令Ψ₁((π/2, φ), λ)=c+ξ，从而得到如下关系式：

$ c + \xi = k\delta \sin \varphi + {\mathit{\Psi }_0}\left( {\left( {{\rm{ \mathtt{ π} }}/2, \varphi } \right), \lambda } \right) $

(7)

由UCA的旋转不变性可知，单元天线0和单元天线1相位中心的位置坐标存在以下关系式：

$ {\mathit{\boldsymbol{p}}_0} = \left[ {\begin{array}{*{20}{c}} {{x_0}}\\ {{y_0}}\\ 0 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \gamma }&{ - \sin \gamma }&0\\ {\sin \gamma }&{\cos \gamma }&0\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{x_1}}\\ {{y_1}}\\ 0 \end{array}} \right] = \mathit{\boldsymbol{M}}{\mathit{\boldsymbol{p}}_1} $

(8)

其中：M是Givens旋转矩阵，γ是单元天线间的角度间隔.由式(8)可知，式(7)是关于方位角φ和(x₀, y₀, 0)的函数.式(7)两边对x₀, y₀, φ求导，然后利用最小二乘法求出相位扰动‖ξ‖²最小时的视在相位中心：

$ \left. \begin{array}{l} \frac{{\partial {\mathit{\Psi }_0}}}{{\partial {x_0}}} = \frac{k}{2}\left( {\sin \varphi - \text{tr}\left( {{\mathit{\boldsymbol{M}}^{\rm{T}}}\mathit{\boldsymbol{M}}} \right)\cos \varphi } \right)\left( {\frac{{\partial \mathit{\boldsymbol{p}}_0^{\rm{T}}}}{{\partial x}}{\mathit{\boldsymbol{p}}_0} + \mathit{\boldsymbol{p}}_0^{\rm{T}}\frac{{\partial {\mathit{\boldsymbol{p}}_0}}}{{\partial x}}} \right)\\ \frac{{\partial {\mathit{\Psi }_0}}}{{\partial {y_0}}} = \frac{k}{2}\left( {\sin \varphi - \text{tr}\left( {{\mathit{\boldsymbol{M}}^{\rm{T}}}\mathit{\boldsymbol{M}}} \right)\cos \varphi } \right)\left( {\frac{{\partial \mathit{\boldsymbol{p}}_0^{\rm{T}}}}{{\partial y}}{\mathit{\boldsymbol{p}}_0} + \mathit{\boldsymbol{p}}_0^{\rm{T}}\frac{{\partial {\mathit{\boldsymbol{p}}_0}}}{{\partial y}}} \right)\\ \frac{{\partial {\mathit{\Psi }_0}}}{{\partial \varphi }} - k\left( {{{\left\| {{\mathit{\boldsymbol{p}}_0}} \right\|}_{\rm{F}}}} \right)\cos \varphi + {\left\| {\mathit{\boldsymbol{M}}{\mathit{\boldsymbol{p}}_0}} \right\|_{\rm{F}}}\sin \varphi = 0 \end{array} \right\} $

(9)

由式(9)可以确定单元天线0在E面内的相位中心，利用UCA的旋转不变特性，可以得到单元天线l(-N≤l≤N)在E面内的相位中心，结合位置矢量以及它们与等效阵列中心的几何关系，可以推导出E面内该虚拟阵列有效孔径的表达式.对于波长λ的来波信号，虚拟阵列的有效孔径可表示为

$ D = 2R = \frac{{\left\| {{\mathit{\boldsymbol{p}}_0} - {\mathit{\boldsymbol{p}}_1}} \right\|}}{{\sin \left( {0.5\gamma } \right)}} $

(10)

D与来波信号波长有关. R取值是D的一半，称为半有效孔径.实际阵列的中心C与等效阵列中心C′并不是完全重合的.如果不考虑单元天线的加工安装误差及其在阵列中的位置偏差，忽略单元天线间的耦合因素，那么当单元天线的相位方向图在主波瓣的最大辐射方向上完全对称时，实际阵列的几何中心才能与虚拟等效阵列的中心重合.

2 基于相位中心的DOA估计模型

当来波信号落在天线主波瓣而不是旁瓣内时，感应电场幅度最大，此时接收信号具有较低的峰值旁瓣比，而且基于相位中心的远场相位近似为常数.此时并不是阵列中所有的单元天线都参与测向，参与测向的单元天线有效辐射区域只能在天线主波瓣内，且不能超出天线的半功率波瓣宽度.

假设一来波方向为(π/2, φ)的远场窄带信号入射到由M个定向天线组成的内向型UCA(如图 1所示的水平极化的对数周期偶极子天线阵列)，这里仅讨论与大地平行单元天线E面上的功率方向图特性，为了推导方便，令G(φ)=G(π/2, φ).该类型单元天线的功率方向图函数^[12]表示为

$ G\left( \varphi \right) = {\cos ^n}\left( {\varphi /2} \right) $

(11)

其中n是与半功率波瓣宽度2θ_0.5有关的参数，其近似值n=lg 0.707/lg[cos(θ_0.5/2)].根据天线半功率波瓣宽度2θ_0.5，可以推导出参与测向的单元天线总数2N+1= $\left\lfloor {2{\theta _{0.5}}/\gamma + 1} \right\rfloor $，其中N < (M－1)/2.以单元天线0为基准，左右延展N个单元天线构成可测向扇区，该测向扇区方位集合Φ={φ|－θ_0.5≤φ≤θ_0.5}.以UCA的圆心为参考点，测向扇区中第l个单元天线接收信号x_l(t)可表示为

$ {x_l}\left( t \right) = {F_l}\left( \varphi \right){{\rm{e}}^{ - {\rm{j}}kR\cos \left( {\varphi - l\gamma } \right)}}s\left( t \right) + {n_l}\left( t \right) $

(12)

其中：－N≤l≤N；T为快拍数，t=1, 2, …, T；n_l(t)为该单元天线l接收到的高斯白噪声；s(t)为信号复包络；F_l(φ)为第l个单元天线的方向图，它反映了单元天线的功率和相位特性，可表示为

$ {F_l}\left( \varphi \right) = G\left( {\varphi - lr} \right){{\rm{e}}^{ - {\rm{j}}{P_l}\left( {\varphi - l, {\xi _l}} \right)}}g\left( {\varphi - lr} \right) $

(13)

其中：ξ_l为第l个单元天线在远场区的相位扰动；g(φ)为单位限幅函数，可用2个阶跃函数表示为

$ g\left( \varphi \right) = U\left( {\varphi + {\theta _{0.5}}} \right) - U\left( {\varphi - {\theta _{0.5}}} \right) $

(14)

P_l(φ, ξ_l)为相位分量，其在单元天线主波瓣内服从均匀分布，其概率密度函数f_l(φ|ξ_l)表示为

$ {f_l}\left( {\varphi \left| {{\xi _l}} \right.} \right) = \left\{ {\begin{array}{*{20}{l}} {\frac{{c + {\xi _l}}}{{2{\theta _{0.5}}}}, }&{ - {\theta _{0.5}} \le \varphi \le {\theta _{0.5}}}\\ {0, }&{其他} \end{array}} \right. $

(15)

为不失一般性，假设有K(0 < K < N)个来波方向φ_m(m=1, 2, …, K)的相互独立窄带信号入射，信号包络s(t)=[s₁(t), s₂(t), …, s_m(t), …, s_K(t)](m=1, 2, …, K).这些信号都落在测向扇区Φ中，那么式(12)表示为

$ \mathit{\boldsymbol{x}}(t) = \sum\limits_{m = 1}^K \mathit{\boldsymbol{a}} \left( {{\varphi _m}} \right){s_m}(t) + \mathit{\boldsymbol{n}}(t) $

(16)

其中：x(t)为阵列接收信号矢量，n(t)为噪声矢量.第m个来波信号的导向矢量a(φ_m)表示为

$ \mathit{\boldsymbol{a}}\left( {{\varphi _m}} \right) = {\mathit{\boldsymbol{F}}_d}\left( {{\varphi _m}} \right) \odot \mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over a} }}\left( {{\varphi _m}} \right) $

(17)

其中：“⊙”是Hadamard乘积；F_d(φ_m)是方向性导向矢量，反映了第m个来波信号在测向扇区Φ中各单元天线主波瓣内的感应电场的幅相关系，其可表示为

$ {\mathit{\boldsymbol{F}}_d}\left( {{\varphi _m}} \right) = {\left[ {{F_{ - N}}\left( {{\varphi _m}} \right), \cdots , {F_0}\left( {{\varphi _m}} \right), \cdots , {F_N}\left( {{\varphi _m}} \right)} \right]^{\rm{T}}} $

(18)

$\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over a} }}$(φ)是把圆阵中的各个单元天线视作理想点源时的导向矢量，可表示为

$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over a} }}\left( {{\varphi _m}} \right) = \left[ {{{\rm{e}}^{ - {\rm{j}}kR\cos \left( {{\varphi _m} + N\gamma } \right)}}, {{\rm{e}}^{ - {\rm{j}}kR\cos \left( {{\varphi _m} + \left( {N - 1} \right)\gamma } \right)}}, \cdots , } \right.}\\ {{{\left. {{{\rm{e}}^{ - {\rm{j}}kR\cos \left( {{\varphi _m} - N\gamma } \right)}}} \right]}^{\rm{T}}}} \end{array} $

(19)

从中可以看出，如果F_d(φ_m)是单位矢量时，也就是说所有的单元天线各向同性，那么$\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over a} }} $(φ_m)就是全向性理想点源的导向矢量，称为全向性导向矢量.因此，式(16)可以表示为

$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{x}}(t) = \mathit{\boldsymbol{A}}(\varphi )\mathit{\boldsymbol{s}}(t) + \mathit{\boldsymbol{n}}(t) = }\\ {(\mathit{\boldsymbol{F}}(\varphi ) \odot \mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over A} }}(\varphi ))\mathit{\boldsymbol{s}}(t) + \mathit{\boldsymbol{n}}(t)} \end{array} $

(20)

其中：A(φ)=[a(φ₁), a(φ₂), …, a(φ_K)]为阵列流形矩阵，F(φ)=[F_d(φ₁), …, F_d(φ_m), …, F_d(φ_K)]为方向性导向矩阵，$\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over A} }}\left( \varphi \right) = \left[ {\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over a} }}\left( {{\varphi _1}} \right), \cdots , \mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over a} }}\left( {{\varphi _K}} \right)} \right] $为全向性导向矩阵.由式(20)可以得到该阵列信号的自相关矩阵R_x：

$ {\mathit{\boldsymbol{R}}_x} = (\mathit{\boldsymbol{F}} \odot \mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over A} }}){\mathit{\boldsymbol{R}}_{ss}}{(\mathit{\boldsymbol{F}} \odot \mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over A} }})^{\rm{H}}} = {\mathit{\boldsymbol{E}}_s}{\mathit{\boldsymbol{A}}_s}\mathit{\boldsymbol{E}}_s^{\rm{H}} + {\sigma ^2}{\mathit{\boldsymbol{E}}_n}\mathit{\boldsymbol{E}}_n^{\rm{H}} $

(21)

其中：R_ss为无噪声信号的自相关矩阵，σ²为噪声功率，Λ_s为K×K信号协方差矩阵，E_s和E_n分别为信号及噪声特征值矢量张成的(2N+1)×K、(2N+1)×((2N+1)－K)信号子空间和噪声子空间.由独立信号的假设条件可知Rank(R_x)=2N+1(满秩)，根据信号子空间与噪声子空间的正交性，运用多重信号分类的DOA估计方法^[13]，可以得到来波信号的空间谱p(φ)的估计：

$ p(\varphi ) = \left[ {\left( {{{\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over A} }}}^{\rm{H}}} \odot \left( {{\mathit{\boldsymbol{F}}^{\rm{H}}}} \right){\mathit{\boldsymbol{E}}_n}\mathit{\boldsymbol{E}}_n^{\rm{H}}\left( {\mathit{\boldsymbol{F}} \odot \mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over A} }}} \right)} \right)} \right. $

(22)

搜索式(22)谱中K个极小值就可得到来波信号的方位角度${\hat \varphi } $_m：

$ {{\hat \varphi }_m} = \mathop {\text{argmin}}\limits_{\varphi \in \mathit{\Phi }} {\left\| {\left[ {\mathit{\boldsymbol{F}}_d^{\rm{H}}(\varphi ) \odot {{\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over a} }}}^{\rm{H}}}(\varphi )} \right]{\mathit{\boldsymbol{E}}_n}} \right\|^2} $

(23)

3 DOA估计误差

影响DOA估计误差的因素主要是单元天线相位中心或视在相位中心导致的阵列有效孔径偏差以及远场等相球面上的相位扰动.基于对相位中心模型的分析，假设径向方向的阵列孔径存在估计误差ε－R，其中ε为估计值.对于来波方位为φ_m的入射信号，各个单元天线在远场观测点处的等相位球面上存在相互独立的相位扰动ξ_l(－N≤l≤N).此时的导向矢量${\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over a} }}} $(φ_m)可表示为

$ \mathit{\boldsymbol{\hat a}}\left( {{\varphi _m}} \right) = {\mathit{\boldsymbol{c}}_m} \odot \mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over a} }}\left( {{\varphi _m}} \right) \odot {\mathit{\boldsymbol{F}}_d}\left( {{\varphi _m}} \right) $

(24)

其中误差矢量c_m表示为

$ {\mathit{\boldsymbol{c}}_m} = {\left[ {\begin{array}{*{20}{c}} {{{\rm{e}}^{{\rm{j}}\left( {{\xi _{ - N}}/\left( {2{\theta _{0.5}}} \right) - k\left( {\varepsilon - R} \right)\cos \left( {{\varphi _m} + N\gamma } \right)} \right)}}}\\ \cdots \\ {{{\rm{e}}^{{\rm{j}}\left( {{\xi _0}/\left( {2{\theta _{0.5}}} \right) - k\left( {\varepsilon - R} \right)\cos \left( {{\varphi _m}} \right)} \right)}}}\\ \cdots \\ {{{\rm{e}}^{{\rm{j}}\left( {{\xi _N}/\left( {2{\theta _{0.5}}} \right) - k\left( {\varepsilon - R} \right)\cos \left( {{\varphi _m} - N\gamma } \right)} \right)}}} \end{array}} \right]^{\rm{T}}} $

(25)

对式(22)做关于真实值φ_m的一阶Taylor级数展开，并且根据函数极小值条件，可以得到

$ 0 = \dot p\left( {{\varphi _m}} \right) + \ddot p\left( {{\varphi _m}} \right)\left( {{{\hat \varphi }_m} - {\varphi _m}} \right) + o\left( {{{\hat \varphi }_m} - {\varphi _m}} \right) $

(26)

其中：$ {\dot p}$(·)是p(·)关于φ_m的1阶导数，${\ddot p} $(·)是p(·)关于φ_m的2阶导数.由式(26)可得估计值$ {\hat \varphi }$_m与真实值φ_m之间的关系为${{\hat \varphi }_m} - {\varphi _m} \approx - \dot p\left( {{\varphi _m}} \right)/\ddot p\left( {{\varphi _m}} \right) $，从而推导出DOA估计误差Δφ_m的表达式为

$ \Delta {\varphi _m} = {{\hat \varphi }_m} - {\varphi _m} \approx - \frac{{Re\left( {{{\mathit{\boldsymbol{\dot {\hat a}}}}^{\rm{H}}}\left( {{\varphi _m}} \right){{\mathit{\boldsymbol{\hat E}}}_n}\mathit{\boldsymbol{\hat E}}_n^{\rm{H}}\mathit{\boldsymbol{\hat a}}\left( {{\varphi _m}} \right)} \right)}}{{{{\mathit{\boldsymbol{\dot {\hat a}}}}^{\rm{H}}}\left( {{\varphi _m}} \right){{\mathit{\boldsymbol{\hat E}}}_n}\mathit{\boldsymbol{\hat E}}_n^{\rm{H}}\mathit{\boldsymbol{\dot {\hat a}}}\left( {{\varphi _m}} \right)}} $

(27)

其中：$\mathit{\boldsymbol{\dot{\hat{a}}}}\left( {{\varphi }_{m}} \right)=\text{d}\mathit{\boldsymbol{\hat{a}}}\left( \varphi \right)/\text{d}\varphi \left| _{\varphi ={{\varphi }_{m}}}\text{,} \right.$，$ {{{\mathit{\boldsymbol{\hat E}}}_n}}$是噪声子空间的估计值.由式(27)可以得到DOA估计误差Δφ_m与有效孔径估计偏差ε－R和相位扰动ξ_l的关系.其中${{\mathit{\boldsymbol{\hat E}}}_n}\mathit{\boldsymbol{\hat E}}_n^{\rm{H}} $是噪声子空间的正交投影矩阵，由于信号子空间与阵列流形矩阵的列空间同属一个空间集合，所以有如下关系：

$ {{\mathit{\boldsymbol{\hat E}}}_n}\mathit{\boldsymbol{\hat E}}_n^{\rm{H}} = \mathit{\boldsymbol{I}} - \mathit{\boldsymbol{A}}{\left( {{\mathit{\boldsymbol{A}}^{\rm{H}}}\mathit{\boldsymbol{A}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{H}}} $

(28)

如果只有一个来波信号落入测向扇区Φ内，那么有${{\mathit{\boldsymbol{\hat E}}}_n}\mathit{\boldsymbol{\hat E}}_n^{\rm{H}} $=I－1/(2N+1) $，Δφ_m可表示为

$ \begin{array}{*{20}{c}} {\Delta {\varphi _m} = }\\ { - \frac{{\left( {2N + 1} \right)\left( {1 - {{\left| {G\left( {{\varphi _m}} \right)} \right|}^2}} \right)G\left( {{\varphi _m}} \right)G\left( {{\varphi _m}} \right)}}{{\left[ {1 - {G^2}\left( {{\varphi _m}} \right)/\left( {2N + 1} \right)} \right]{\alpha _1} + \left[ {1 + {G^2}\left( {{\varphi _m}} \right)/\left( {2N + 1} \right)} \right]{\alpha _2}}}} \end{array} $

(29)

其中α₁和α₂为

$ \left. \begin{array}{l} {\alpha _1} = \sum\limits_l {\left[ {{G^2}\left( {{\varphi _m}} \right) - {k^2}{\varepsilon ^2}{{\sin }^2}\left( {{\varphi _m} + l\gamma } \right){G^2}\left( {{\varphi _m}} \right)} \right.} \\ {\alpha _2} = \sum\limits_l {\left[ { - 2{\rm{j}}k\varepsilon \sin \left( {{\varphi _m} + l\gamma } \right)G\left( {{\varphi _m}} \right)G\left( {{\varphi _m}} \right)} \right]} \end{array} \right\} $

(30)

其中－N≤l≤N.由式(29)可以看到，DOA估计误差与等相球面上的随机相位偏移ξ_l无关，这是因为随机相位扰动未造成入射方向上的来波信号在各个单元天线上的波程差的偏差，只有那些在径向方向阵列孔径上引起的波程差的偏差的项，即式中的因子项kεsin (φ_m+lγ)才对DOA估计误差产生影响.此外，定向天线的功率方向图对DOA估计误差也有一定影响.实际的天线功率方向图并不是理想的等球面，可以将这种影响看作是包括天线阵列在内的整个测向系统在接收幅度上的误差，通常在系统通路校准问题上加以考虑.假设单元天线的功率方向图G(φ)=1，即理想的全向天线，那么阵列中所有的单元天线都可等效为理想点源，它们的相位中心与其几何中心重合，式(29)中1－|G(φ_m)|²= 0，从而有Δφ_m= 0，也就是说在理想点源组成的天线阵列中，单元天线相位中心对DOA估计精度不会产生影响.

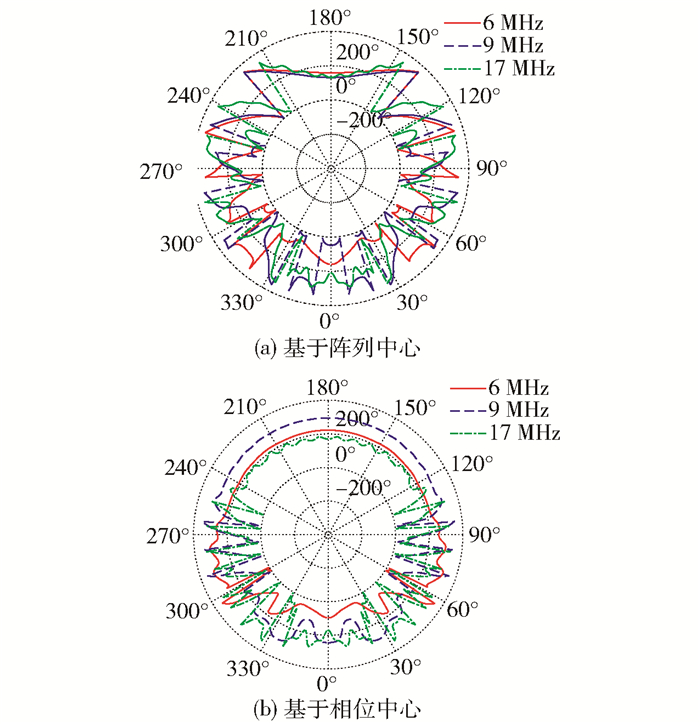
4 实验仿真 4.1 有效孔径分析

一个由24个单元组成的水平极化对数周期UCA，工作频段是3~30 MHz.对于来波方向为(4°, 0°)的信号，分析其在单元天线主波瓣内的幅度和相位响应，得到图 2(a)所示单元天线主波瓣内相位方向图.由相位方向图可知，单元天线的远场相位在主波瓣范围(150°~210°)内并不是等相位面.以9 MHz信号为例，当来波信号以150°方位入射时，其远场相位为256°；以180°入射时，其远场相位为130°.因为单元天线主波瓣内的远场相位变化很大，所以不能以该阵列中心作为相位参考点来进行DOA估计.

根据主波瓣内的远场相位特性估计单元天线的相位中心，进一步推算出单元天线的远场相位值.如图 2(b)所示，通过对6 MHz、9 MHz和17 MHz来波信号的远场相位进行分析，得到基于视在相位中心的远场相位值.与图 2(a)比较可以看到，6 MHz和9 MHz信号入射时，基于视在相位中心的远场相位值在天线主波瓣内服从均匀分布，并不随入射角度的变化而改变，只和来波信号频率有关.随着频率的升高，主波瓣内的相位一致性随之变差，主波瓣宽度也随之减小.在DOA估计的可用主波瓣宽度上，17 MHz信号较6 MHz信号小约50°，而且在其主波瓣内存在一定的相位波动.

图 3给出了阵列半有效孔径随频率变化的关系曲线.图中阴影部分为该定向天线阵列的有效作用区域，从图中可以知道30 MHz时的阵列孔径为67.32 m、3 MHz时的阵列孔径为339.06 m.图中黑色虚线部分为半有效孔径随频率变化时的关系曲线，对比可知定向性天线阵列的有效孔径与来波信号频率并不是呈线性变化关系.在实际的DOA估计中，必须根据图中所示的信号频率与阵列半径的对应关系建立起定向性天线阵列的导向矢量矩阵，这样才能正确地估计出信号的来波方向.

4.2 DOA估计误差分析

接下来从以下几个仿真实验验证新模型的性能，主要验证误差矢量c_m对DOA估计误差的影响，分别考查半功率波瓣宽度2θ_0.5、估计值ε和入射角φ_m因素的影响.

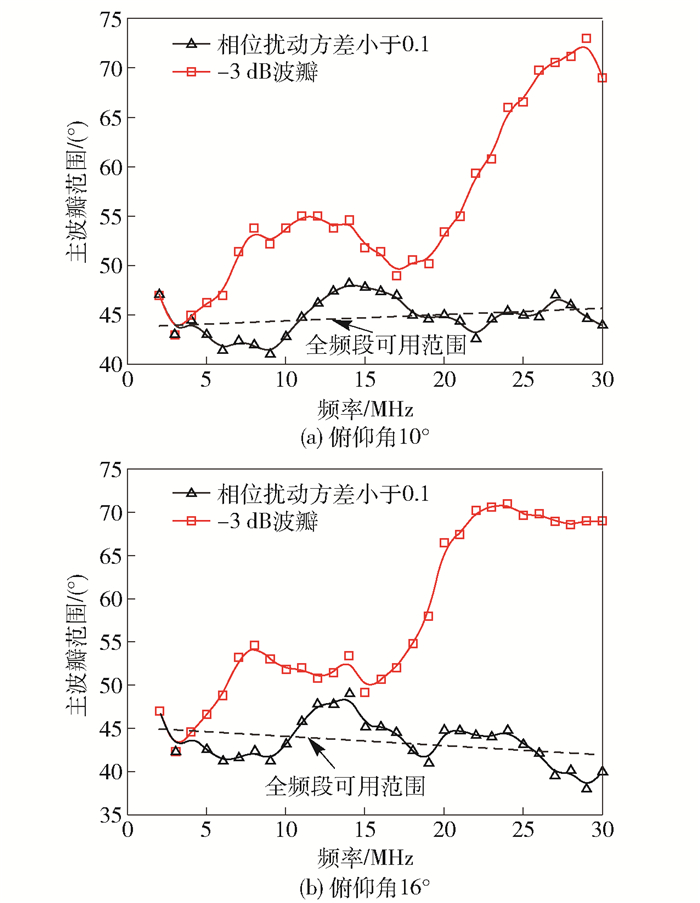
1) 宽频带内DOA估计的主波瓣2θ_0.5的范围问题. 图 4(a)和4(b)给出了俯仰角为10°和16°时全频段内单元天线的半功率波瓣宽度与频率的变化关系.实际工程中的远场相位存在一定的相位波动，在主波瓣内并不服从均匀分布，而是在一定误差范围内的近似逼近.从图中可以看出，相位扰动方差为0.1及俯仰角为10°和16°时的主波瓣宽度，6 MHz时分别由51.4°、53.2°减小到42.4°、41.6°，9 MHz时由53.8°、51.8°减小到42.8°、43.2°；随着频率的升高，满足误差要求的主波瓣宽度逐渐减小，相位扰动因素影响明显.图中虚线表示全频段内可用主波瓣范围.由第2节DOA估计模型可以知道，单元天线的主波瓣宽度决定了参与测向的天线个数.此时，当取2θ_0.5=45°时，参与扇区测向的单元天线个数N=7.这样才能保证在360°方向上所有单元天线主波瓣内的远场相位都是均匀分布的.

2) 宽频带内满足一定的DOA估计精度有效孔径ε的容差问题.在定向性天线组成的UCA中，只有来波信号落入主波瓣内的单元天线才参与测向，这些天线构成了一个测向扇区.这里以信噪比为0、来波方向是(90°, 5°)的信号为例进行仿真.测向扇区范围是0°±45°，单元天线主波瓣宽度为15°，参与测向的单元天线个数为7. 表 1给出了DOA估计误差为0.5°时天线阵列的半有效孔径与频率的变化关系.从中可以看到，随着频率的升高，允许的半有效孔径余量逐渐减小. 6 MHz时估计的半有效孔径是116.01 m，半有效孔径上限为127.01 m，下限为103.01 m；17 MHz时估计的半有效孔径为53.74 m，半有效孔径上限为58.75 m，下限为47.75 m.另外，从表中可以看到，单元天线间隔与波长比值随着频率的升高而增大.为了保证要求的DOA估计精度，需要尽可能地提高单元天线间隔与波长的比值，但是比值的升高则限制了无模糊测向的范围.

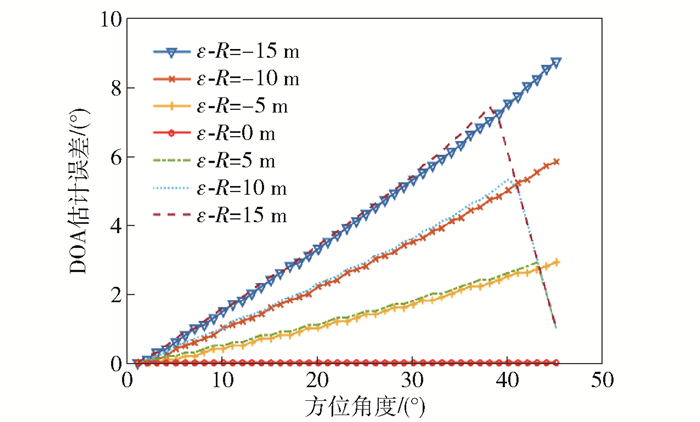
3) DOA估计误差与来波入射角度φ_m的关系. 图 5给出了9 MHz时不同的半有效孔径的估计误差下，DOA估计误差与来波方位角之间的变化关系曲线.从中看出0°方位下的DOA估计误差最小，但随着信号入射方位向+45°方向偏移，DOA估计误差逐渐增加.以40°方位为例，误差为±10 m时，DOA估计误差约为5.2°；误差为±5 m时，DOA估计误差约为3.1°.如果信号入射方位继续偏移以至于超出该扇区测向范围，就导致DOA估计错误.

4.3 对比验证

1) 不同模型下的DOA估计误差对比分析

对常规理想点源DOA估计模型与所提扇区DOA估计模型进行对比分析，对6 MHz、9 MHz和17 MHz来波方位为8°的信号进行DOA估计仿真. 图 6给出了在不同的DOA估计模型下的DOA估计误差与阵列有效孔径估计误差之间的关系曲线.图中虚线对应的是理想点源模型下的仿真结果曲线，实线是采用所提DOA估计模型仿真得到的结果曲线.从中可以看出，在阵列有效孔径估计误差3 m以内，基于相位中心的扇区DOA估计模型的DOA估计误差比理想点源的DOA估计模型要小；在有效孔径估计误差大于3 m时，由于参与DOA估计的单元天线个数(24副)多于扇区DOA估计模型的单元天线个数(7副)，理想点源的DOA估计模型测向精度高于所提出的DOA估计模型，但随着有效孔径估计误差的增大，基于扇区的DOA估计模型的DOA估计误差比理想点源的DOA估计模型要小很多；当有效孔径估计误差大于5 m时，扇区DOA估计模型最大误差仅约为1°，而理想点源的DOA估计模型则出现错误估计值.

2) 实测数据对比验证

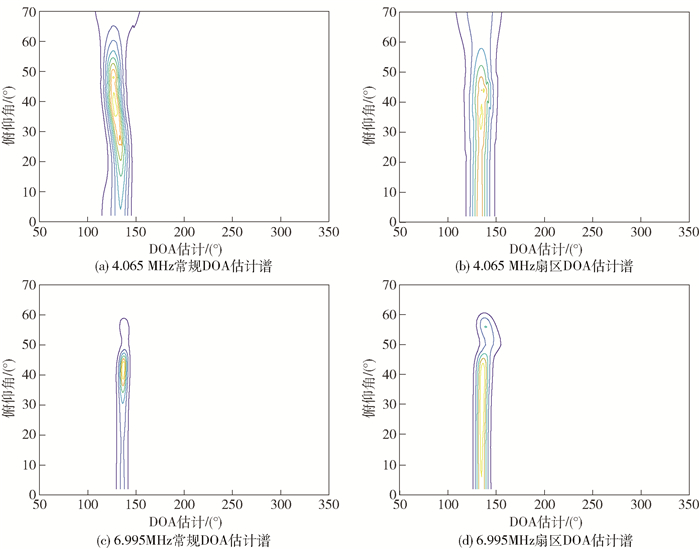
对不同俯仰面上相位中心的远场相位响应进行仿真并利用多重信号分类算法验证外界信号方位.对来自135°方位的4.065 MHz和6.955 MHz信号进行DOA估计验证. 图 7是不同俯仰面相位中心下对来波信号进行的方位DOA估计.其中，图 7(a)、图 7(b)分别是4.065 MHz常规DOA估计谱、扇区DOA估计谱；图 7(c)、图 7(d)分别是6.995 MHz常规DOA估计谱、扇区DOA估计谱.单元天线1取0°指向，那么取单元天线9为基准，左右延展3副天线组成扇区DOA估计阵列.从图 7(a)中可以看出，在俯仰面20°~60°范围内，4.065 MHz信号的常规DOA估计谱的角度估计出现“弯曲”，该估计值随着俯仰面范围的增加出现了较大误差，而图 7(b)在此范围内DOA估计值并没有大的变化；图 7(c)和7(d)中6.995 MHz信号在俯仰面范围内的DOA估计值较为一致.在先验角度和满足一定精度要求下所提的扇区DOA估计模型单元天线参与数量少，谱峰搜索时间也随之减少.

5 结束语

定向性天线在主波瓣某一范围内，基于相位中心的远场相位是恒定的或者是在一定相位扰动下的近似逼近，这样既可以确定参与测向的主波瓣的宽度，又可以估计出相位中心的相对位置.笔者引入方向性矢量及误差矢量对理想点源的DOA估计模型进行改进，对落入某一测向扇区内的信号进行DOA估计，解决定向性天线阵列的DOA估计问题.通过仿真对定向性天线阵列DOA估计的影响因素进行分析，验证了模型的正确性和有效性并给出影响DOA估计精度的有效孔径的误差范围.不过这主要是针对落入单个扇区的来波信号的实验仿真，跨扇区或多个独立扇区多个来波信号的DOA估计算法还需进一步研究.