提出了一种集随机接入和功率控制于一体的多读写器抗干扰联合优化算法,可根据读写器密度自适应调节2种作用的权重.首先全面考虑接入概率、功率大小和信道选择对读写器信噪比的影响,将多读写器抗干扰问题建模成混合-整数规划问题;其次采用广义Benders分解方法将算法分解成易求解的子问题和二进制规划主问题,并证明了算法收敛于全局最优解;最后通过仿真验证了算法在标签识别率和公平性方面优于现有方案.
A joint anti-interference optimization algorithm for multiple readers is proposed, which integrates random access and power control strategies. Firstly, considering the effects of access probability, transmitting power and channel selection on the signal-to-noise ratio (SNR) of the reader, the anti-interference problem of multiple readers is modeled as a mixed integer programming problem. Secondly, the generalized Benders decomposition method is used to decompose the algorithm into an easy-to-solve primal problem and a master problem of binary programming. It is proved that the algorithm converges to the global optimal solution. Finally, the simulation results show that the algorithm outperforms the existing schemes in tag recognition rate and fairness.
射频识别(RFID, radio frequency identification)系统由读写器和标签构成.标签一般为无源结构,从接收的读写器信号中获取能量,通过调制反向散射信号与读写器通信.标签发回读写器的反向散射信号较弱,极易受到周围环境的干扰.尤其在多读写器应用场景中,每个读写器都受到邻近读写器同频干扰信号的影响,当干扰较强时,标签识别率会大幅下降,这种情况一般称为读写器冲突问题[1-2].
国内外已对读写器间干扰问题开展了大量研究工作,相关的研究文献可分为两大类.一类是时域防碰撞策略[3-6],即设法使读写器时分复用信道,在时域上避免重叠.例如,Ferrero等[3]和Mitton等[4]采用动态调整接入优先级的防碰撞方式;Amadou等[5]通过动态调整竞争窗口使各读写器获得公平的吞吐量;Vales等[6]提出根据读写器负荷规划接入时间的方法.另一类是功率调整策略[7-10],即各读写器通过调节发射功率,达到降低对外干扰和提高自身信噪比的目的.但无论是时域防碰撞算法还是功率控制算法,都仅从时域或功率的单一角度考虑,存在很大的局限性.在移动读写器应用场景下,读写器密度经常发生变化,如能将接入时间和功率控制方法综合使用,根据实际情况灵活调整2种方法的作用权重,能更有效地解决移动读写器应用场景下读写器间的干扰问题.
笔者在综合分析时域防碰撞和功率控制2类算法的基础上,提出一种基于功率调整与随机接入联合优化的多读写器抗干扰算法.该算法可根据读写器检测的信噪比自动调节发射功率、接入时间和信道选择.由于综合了接入时间控制和功率控制的优点,对不同的读写器分布密度均能起到良好的干扰抑制作用,提高了对实际应用场景的适用性.
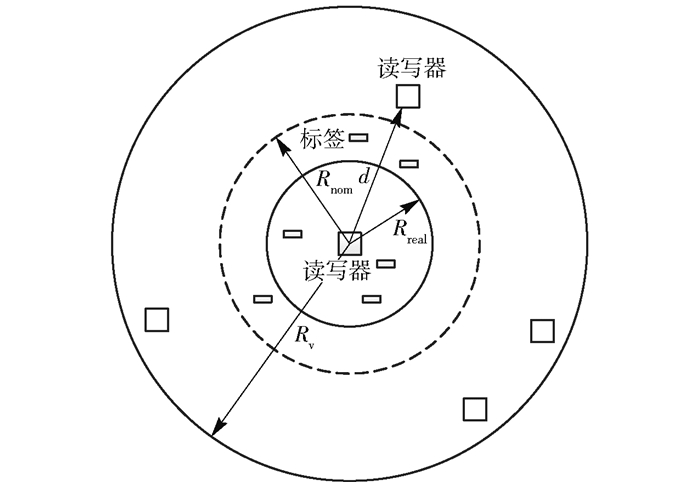
1 多读写器干扰问题场景描述根据参考文献[7]给出的读写器干扰模型,所讨论的典型应用场景如图 1所示.假设n个读写器分布于半径为Rv的区域内,读写器功率可调,并有下述条件设定.
|
图 1 多读写器干扰场景 |
1) 读写器间距离d大于预设的最小距离rmin,使读写器识别范围不发生重叠.
2) 读写器间信号传播路径损耗与dγ成正比关系,γ为一常数.
3) 读写器干扰类型为加性.
4) 读写器工作信道可在m个信道中随机选择.
当处于活动状态时,每个读写器向其识别范围内的标签发出轮询命令,标签根据预定的通信协议,通过反向散射调制信号将ID信息返回读写器.每个读写器发射的信号会对其他读写器产生干扰,该干扰随区域内读写器数量的增加而加剧.设读写器r在信道c上工作,其收到相距1 m标签的反向散射信号功率表示为[2]
| $ q_{r, c}^R = \alpha {E_\text{tag}}{q_{r, c}}{G_{\rm{T}}}{G_{\rm{R}}}P_0^2 = {A_{r, c}}{q_{r, c}} $ | (1) |
其中:Ar, c=αEtag GT GR P02,qr, c为总传输功率,p0为1 m长度的路径损耗参考值,Etag为标签反向散射系数,GT、GR分别为发射天线和接收天线的增益,α为所用频段内发射功率占总功率的比例,该值与信号调制方式有关.当读写器和标签位置固定后Ar, c为常数.
如果2个读写器距离为d,则其中一个读写器s对另一个读写器r的干扰功率可表示为
| $ {I_{s, r}} = h{q_{s, c}}\beta {G_{\rm{T}}}{G_{\rm{R}}}{P_0}{d^{ - \gamma }} = {B_{s, c}}{q_{s, c}} $ | (2) |
其中:Bs, c=hβGT GR P0d-γ,h为两读写器间的信道衰落系数,β为频谱模板限值[10].当读写器和标签位置固定后Bs, c为常数.
读写器发出轮询命令后,接收到标签的反向散射信号,同时受到邻近处于活动状态读写器的干扰信号影响.设读写器r工作在信道c上,信道噪声为Nc,受到邻近处于活动状态同频读写器i的干扰功率为Ii, r,则读写器r接收端的信噪比为
| $ J\left( {r, c} \right) = \frac{{{A_{r, c}}{q_{r, c}}}}{{\sum\limits_{i \ne r} {{I_{i, r}}} + {N_c}}} $ | (3) |
由式(3)可见,读写器接收端信噪比与其发射功率成正比,与活动状态读写器干扰功率成反比,因此需要设计合适的功率和活动状态控制策略,以保证多读写器性能提升的公平性.
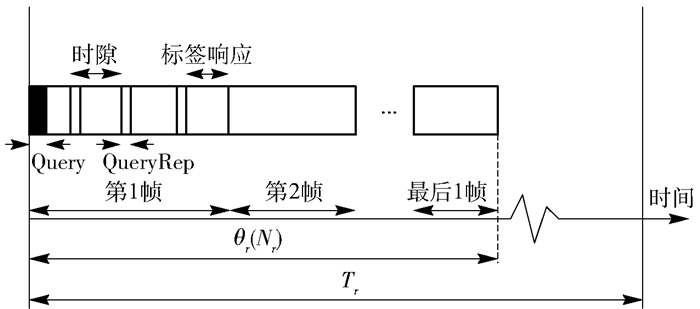
2 多读写器干扰问题建模 2.1 读写器与标签MAC层通信协议一个典型的RFID系统包括读写器和多个标签,读写器和标签间共享同一信道,当多个标签同时响应读写器命令时将发生碰撞现象.笔者以应用最广的并已标准化的MAC层协议EPCglobal Class-1 Generation-2(C1G2)[11]为研究对象.根据该协议,每个读写器执行周期为Tr的轮询操作,如图 2所示.在每个轮询周期的开始,读写器随机选择是否执行轮询,采用哪个信道以及发射功率大小.为分析问题方便,将R、C和U分别定义为读写器集合、信道集合和功率集合,将pr, c定义为读写器r在信道c上执行轮询的概率,qr, c定义为读写器r在c上的发射功率,其中r∈R,c∈C,q∈U.在C1G2协议中,读写器首先发出Query命令启动第1帧,该帧的其他部分包含一系列时隙,每个标签随机选择一个时隙发送响应信息.每帧结束后,读写器根据各个时隙的响应情况(有空闲、成功和碰撞3种类型),采用合适的算法估计标签个数Nr,计算最优帧长,启动下一帧.将θr(Nr)定义为读写器r的有效轮询时间,Tr定义为轮询周期,并假定各读写器轮询周期相等,即Tr=T,∀r∈R.
|
图 2 读写器轮询操作 |
下面分析读写器执行轮询时的相互干扰问题.考虑仅存在2个读写器的简单场景,当2个读写器r和s的轮询周期存在交叠时,可能的干扰情况有3种.
1) 读写器r和s分别采用信道c1和c2执行轮询,则不会发生碰撞,读写器r的信噪比为
| $ J\left( {r, {c_1}} \right) = \frac{{{A_{r, {c_1}}}{q_{r, {c_1}}}}}{{{N_{{c_1}}}}} $ | (4) |
其中Nc1为信道c1的噪声.
2) 读写器r和s采用相同的信道c1轮询,但有效轮询时间不存在交叠,读写器r的信噪比仍可由式(4)计算.
3) 读写器r和s采用相同的信道c1轮询,有效轮询时间存在交叠,读写器r处于未交叠部分的信噪比可由式(4)计算,处于交叠部分的信噪比为
| $ J\left( {r, {c_1}} \right) = \frac{{{A_{r, {c_1}}}{q_{r, {c_1}}}}}{{{B_{s, {c_1}}}{q_{s, {c_1}}} + {N_{{c_1}}}}} $ | (5) |
将以上分析推广到更多读写器的情况,可以得出以下定理.
定理1 假设轮询周期T足够长,大于等于有效轮询时间的2倍,即
| $ \mathop {\max }\limits_{r \in R} {\theta _r}\left( {{N_r}} \right) \le T/2 $ | (6) |
则对任意读写器r∈R,工作在信道c上受其他读写器的平均干扰功率为
| $ {{\bar q}_{{\rm{itf}}}}\left( {r, c} \right) = \sum\limits_{i \ne r, {c_i} = c} {{B_{i, {c_i}}}} {q_{i, {c_i}}}{p_{i, {c_i}}}\frac{{{\theta _i}\left( {{N_i}} \right)}}{T} $ | (7) |
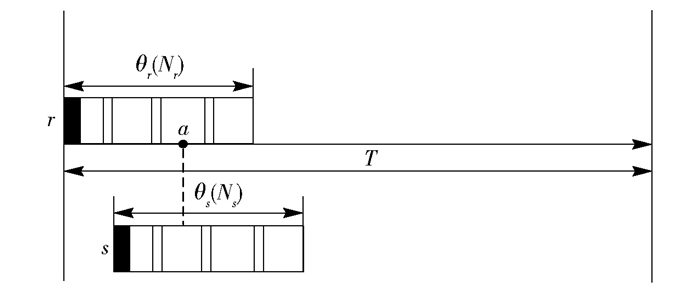
证明 如图 3所示,首先考虑仅有2个读写器r和s的情况.读写器r在信道c上发出轮询后,轮询帧中任一点a与读写器s冲突的概率为
|
图 3 2个读写器发生轮询冲突的情况 |
根据定理1,定义读写器r在c上的平均信噪比为
| $ \bar J\left( {r, c} \right) = \frac{{{A_{r, c}}{p_{r, c}}{q_{r, c}}}}{{{{\bar q}_{{\rm{itf}}}}\left( {r, c} \right) + {N_c}}} $ | (8) |
通过定义式(8),将读写器信噪比与区域内其他读写器轮询概率、发射功率和信道选择相关联,可以联合发挥接入控制和功率控制的作用,充分结合二者的优点提高干扰抑制效果.
2.2 多读写器信噪比优化模型对每个读写器r∈R和任意信道c∈C,定义信道选择变量为
| $ {v_{r, c}} = \left\{ \begin{array}{l} 1, \;\;\;读写器\;r\;选择信道\;c\\ 0, \;\;\;读写器\;r\;不选择信道\;c \end{array} \right. $ | (9) |
因为每个读写器仅工作在1个信道上,所以
| $ \mathop \sum \limits^{c \in C} {v_{r, c}} = 1, \;\;\;\;\forall r \in R $ | (10) |
如果读写器r不工作在信道c,则读写器在信道c上的轮询概率和功率均为零.因此,无论读写器r是否工作在信道c,都有
| $ {p_{r, c}} \le {v_{r, c}}, {q_{r, c}} \le {v_{r, c}}{q_{\max }}, \forall r \in R, c \in C $ | (11) |
其中qmax为读写器发射功率上限.
定义P、V和Q分别为轮询概率、信道选择和发射功率的可行矢量集,即
| $ \mathit{\boldsymbol{P}} = \left\{ {\mathit{\boldsymbol{p}}:{p_{r, c}} \le {v_{r, c}}, {p_{r, c}} \in \left[ {0, 1} \right], \forall r \in R, c \in C} \right\} $ | (12) |
| $ \mathit{\boldsymbol{V}} = \left\{ {\mathit{\boldsymbol{v}}:\sum\limits_{c \in C} {{v_{r, c}}} = 1, {v_{r, c}} \in \left\{ {0, 1} \right\}, \forall r \in R, c \in C} \right\} $ | (13) |
| $ \mathit{\boldsymbol{Q}} = \left\{ {\mathit{\boldsymbol{q}}:{q_{r, c}} \le {v_{r, c}}{q_{\max }}, {q_{r, c}} \in \left[ {0, {q_{\max }}} \right], \forall r \in R, c \in C} \right\} $ | (14) |
笔者提出基于功率调整与随机接入联合优化的多读写器抗干扰方法,其基本思想是,选择合适的p、v和q,使所有读写器的平均信噪比都能达到最大-最小公平原则下的最优值,将功率、时间和信道资源平均分配给各读写器.根据最大-最小公平原则,当p、v和q满足最大-最小公平条件时,对任意读写器r以及工作在相同信道c上的读写器集合S={s:J(s, c)≤J(r, c), ∀s∈R, s≠r},增大r的信噪比,必会导致S中某个读写器信噪比的下降.可将上述描述转化为以下非线性优化问题[12]:
| $ \begin{array}{*{20}{c}} {\mathop {\rm{ maxmize }}\limits_{p \in \mathit{\boldsymbol{P}}, v \in \mathit{\boldsymbol{V}}, q \in \mathit{\boldsymbol{Q}}} \sum\limits_{r \in R} f \left( {\bar J\left( {r, c} \right)} \right)}\\ {{\rm{s}}.\;{\rm{t}}.\;\bar J\left( {r, c} \right) \ge \min \_J, r \in R, c \in C} \end{array} $ | (15) |
其中:f(J(r, c))=-(J(r, c))-10,vr, c=1,min _J为读写器正常工作的信噪比下限.因f(J(r, c))为非凸函数,且vr, c为二进制数,该问题属于混合整数规划问题,无法用常规的凸优化方法求解,下节重点介绍该问题的求解.
3 多读写器信噪比优化算法f(J(r, c))的非凸特性和混合整数规划特性为问题的求解带来了困难.针对该问题的特点,采用广义Benders分解方法[13],将问题式(15)分解为2个问题:
1) 子问题,即固定v,研究问题式(15)关于p和q的连续变量优化问题;
2) 主问题,即固定p和q,研究问题式(15)关于v的离散变量优化问题.
上述子问题的解为问题式(15)提供了下界,主问题的解为问题式(15)提供了上界[13].在满足一定条件时,经过不断迭代得出的上界和下界可在有限次迭代次数内收敛于同一点,该点就是问题式(15)的全局优化解.以下分别介绍子问题和主问题的求解方法.
3.1 子问题的求解给定任意信道选择矢量v∈V,将问题式(15)的子问题定义为
| $ \begin{array}{*{20}{c}} {\mathop {\rm{ maxmize }}\limits_{p \in \mathit{\boldsymbol{P}}\left( v \right), q \in \mathit{\boldsymbol{Q}}\left( v \right)} \sum\limits_{r \in R} f \left( {\bar J\left( {r, c} \right)} \right)}\\ {{\rm{s}}.\;{\rm{t}}.\;\bar J\left( {r, c} \right) \ge \min \_J, r \in R, c \in C} \end{array} $ | (16) |
该子问题的目标函数与问题式(15)相同,区别在于此式中信道矢量v为固定值,p和q仅在此固定信道上取值.子问题式(16)仍不是凸优化问题,但如果只允许某个pr, cr或qr, cr变化,而固定p和q中的其他变量,则可以将式(16)转化为一系列只针对某个特定pr, cr或qr, cr的凸优化问题.下面通过定理2予以证明.
定理2 给定信道选择矢量v∈V,对于任意pr, cr,如果固定所有ps, cs(s∈R, s≠r, vs, cs=1)和qs, cs(s∈R, vs, cs=1)的值,则子问题式(16)是关于pr, cr的凸优化问题;同理,对于任意qr, cr,如果固定所有qs, cs(s∈R, s≠r, vs, cs=1)和ps, cs(s∈R, vs, cs=1)的值,则子问题式(16)是关于qr, cr的凸优化问题.
证明 给定信道选择矢量v∈V,令g(p, q)=
| $ \frac{{{\partial ^2}g}}{{\partial p_{r, {c_r}}^2}} \le 0 $ | (17) |
| $ \frac{{{\partial ^2}e\left( {s, \mathit{\boldsymbol{p}}, \mathit{\boldsymbol{q}}} \right)}}{{\partial p_{r, {c_r}}^2}} = 0, s = r, \forall r, s \in R $ | (18) |
| $ \frac{{{\partial ^2}e\left( {s, \mathit{\boldsymbol{p}}, \mathit{\boldsymbol{q}}} \right)}}{{\partial p_{r, {c_r}}^2}} \le 0 $ | (19) |
由式(17)~式(19)可见,对于任意pr, cr,子问题式(16)的目标函数是凸函数,约束条件是凹函数,因此该问题对于pr, cr是凸优化问题[14-15].
对于任意qr, cr,可求出:
| $ \frac{{{\partial ^2}g}}{{\partial q_{r, {c_r}}^2}} \le 0 $ | (20) |
| $ \frac{{{\partial ^2}e\left( {s, \mathit{\boldsymbol{p}}, \mathit{\boldsymbol{q}}} \right)}}{{\partial q_{r, {c_r}}^2}} = 0, s = r, \forall r, s \in R $ | (21) |
| $ \frac{{{\partial ^2}e\left( {s, \mathit{\boldsymbol{p}}, \mathit{\boldsymbol{q}}} \right)}}{{\partial q_{r, {c_r}}^2}} \le 0 $ | (22) |
由式(20)~式(22)可见,对于任意qr, cr,子问题式(16)的目标函数是凸函数,约束条件是凹函数,因此该问题对于qr, cr是凸优化问题.证毕.
尽管问题式(16)本身不是凸优化问题,但根据定理2,可以采用循环迭代的方式求出最优解.设所有pr, cr, qr, cr(r∈R, vr, cr=1)构成的集合为{pr1, c1, qr1, c1, pr2, c2, qr2, c2, …, prn, cn, qrn, cn},以循环迭代的方式,每次迭代只针对集合中的1个变量并固定其他变量求问题式(16)的最优解.如第1次迭代只针对pr1, c1并固定其他变量,可求出最优解pr1, c1*(1),第2次迭代只针对qr1, c1并固定其他变量,可求出最优解qr1, c1*(1),以此类推.这样,第1次循环可依次得到最优解pr1, c1*(1), …, qrn, cn*(1),然后再进行第2次循环可得pr1, c1*(2), …, qrn, cn*(2),这样继续进行下去直至前后2次循环得到的解的差异小于指定值为止.
下面简要分析这种循环迭代方法的收敛性.通过3.1述过程可以明显看出,问题式(16)在第k+1次迭代的目标函数值要大于第k次迭代值,这样问题式(16)的一系列迭代值构成一单调递增序列.因信噪比的有界性,问题式(16)的目标函数值也是有界的,根据单调有界数列必有极限,问题式(16)的迭代值序列必然收敛.
3.2 主问题的求解在固定信道矢量v的条件下,通过3.1节的方法可求出p和q的最优解.信道矢量v的最优值可通过求解主问题获得.令v*(k)为主问题的第k次迭代解,其中v*(1)为随机取值.给定v*(k)∈V,令p*(k)、q*(k)为当固定v*(k)时子问题式(16)的解.令λ*(k)=(λr, c*(k), ∀r∈r, c∈C)为对应约束条件的拉格朗日系数矢量,根据文献[13],建立主问题的第k+1次迭代形式为
| $ \begin{array}{*{20}{c}} {{\rm{s}}.\;{\rm{t}}.\;\;y \le \sum\limits_{r \in R}^{\mathop {\max {\rm{mize}}}\limits_{v \in \mathit{\boldsymbol{V}}, y \ge 0} } {\sum\limits_{c \in C}^y {\left[ {\lambda _{r, c}^{ * \left( i \right)}\left( {{v_{r, c}} - p_{r, c}^{ * \left( i \right)}} \right)} \right]} } + }\\ {{{\left. {\sum\limits_{r \in R} f \left( {\bar J\left( {r, c} \right)} \right)} \right|}_{p = {p^{ * \left( k \right)}}, q = {q^{ * \left( k \right)}}}}, \;\;\;\;\forall i = 1, 2, \cdots , k} \end{array} $ | (23) |
因vr, c∈{0, 1},该主问题属于二进制线性规划问题,可以用割平面法或隐数法求解[14].
3.3 多读写器信噪比优化算法实现流程综合3.1节和3.2节关于主问题和子问题的定义和求解方法,所设计的多读写器信噪比优化算法流程如图 4所示.多读写器信噪比优化算法的实现采用集中式结构,整个系统包括多个读写器和1台中心服务器,算法在中心服务器上运行.中心服务器在运行过程中实时收集各读写器的状态数据,通过多读写器信噪比优化算法求出最优的读写器运行参数p、v和q,由专用信道广播给各读写器.多读写器信噪比优化算法是一个不断迭代的过程,在第k次迭代先固定v*(k)计算子问题的目标值F*(k),求出p*(k)和q*(k),然后固定p*(k)和q*(k)计算y*(k+1)和v*(k+1).预设一较小正数ε作为终止条件,每次迭代结束后判断y*(k)-F*(k)≤ε是否成立,即上界序列和下界序列是否收敛到同一点.如果满足,则迭代值符合要求,更新各个读写器的参数;如果不满足,则继续迭代.

|
图 4 多读写器信噪比优化算法流程 |
将所提方案与4个方案进行对比,分别是仅考虑避免时域防碰撞的分布式公平(DFA, distributed & fair anticollision)[4]和自适应(HA, high adaptive)[5]方案以及读写器和标签位置固定的最小代价功率分配(MR2D, minimum-cost RFID reader deployment)[8]和自适应功率分配方案(APC, adaptive power control)[9].读写器最大功率限制均为1 W,信道数目为20,信道类型为加性高斯白噪声信道,噪声系数为10 dB.读写器和标签均为随机分布,读写器间最小距离为5 m,读写器与标签间的最小距离为0.2 m.结合文献[7]中的仿真条件,将式(1)、式(2)中参数设置为α=0.86,Etag =0.1,GT =GR =6 dBi,P0=-31.6 dB,h=1,β=-1.9,γ=2.5.
首先将平均标签读取成功率作为衡量算法整体性能的指标.平均标签读取成功率是不考虑标签碰撞时,读写器对单标签时隙读取成功的概率,影响该指标的因素主要是各读写器功率大小和读写器间的碰撞概率.如图 5所示,MR2D在读写器密度较大的局部位置读取成功率下降较大,平均标签读取成功率较低;APC方案根据读写器的位置调整各读写器功率大小,保证了一定程度的公平性,但读写器密度较大时碰撞机率的增加使相互间干扰加剧,功率调节的作用有限;载波侦听方案在读写器密度较大、时域碰撞频繁时效果要好于功率调节方案,但读写器密度较小时,性能要低于功率分配方案;所提算法综合了功率调节和载波侦听的优势,采用功率调节和随机接入相结合的方式,在读写器密度从小到大范围内都能保持良好的性能,效果要优于单纯的功率分配和载波侦听方案.

|
图 5 平均标签读取成功率的比较 |
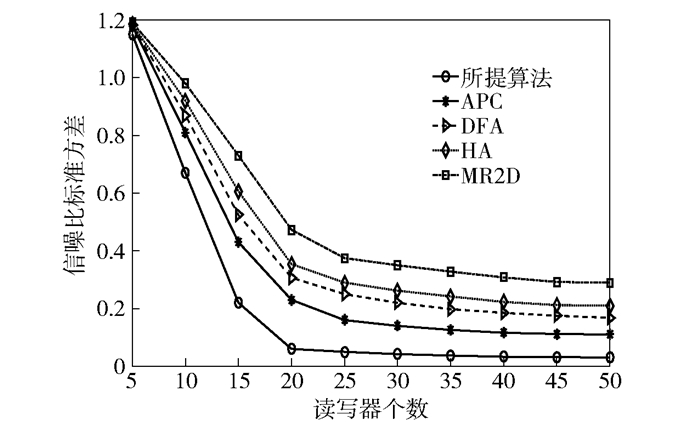
其次将信噪比标准方差作为衡量算法公平性的指标.如图 6所示,MR2D算法在读写器与标签位置固定的条件下分配功率,但当读写器位置随机分布(读写器或标签处于移动状态)时,密度较高区域读写器的信噪比下降较多;APC算法考虑了读写器密度不同的差异性,信噪比标准方差比固定功率分配算法低;载波侦听方案通过避免时域碰撞的方法可减少轮询次数,但都属于启发式算法,不能从全局角度进行系统优化;由于所提算法综合了时域防碰撞和功率控制的优点,保证了时间资源、信道资源和功率资源在各读写器间分配的公平性,受读写器密度变化影响较小,该指标要优于其他算法.
|
图 6 信噪比标准方差的比较 |
各算法的平均数据吞吐量性能比较如图 7所示.平均数据吞吐量定义为单位时间内读写器正确读取的比特数.平均数据吞吐量受读写器密度、发射功率、轮询概率的直接影响,是衡量读写器工作效率的重要指标.由图 7可见,当读写器密度较低时,几种算法的平均数据吞吐量都较高,随着读写器密度增加,读写器间干扰加剧,载波侦听方案的平均数据吞吐量性能要优于功率控制方案,所提算法的平均数据吞吐量性能始终高于其他算法.

|
图 7 平均数据吞吐量的比较 |
所提算法收敛性能如图 8所示.根据第3节的分析,主问题的解和子问题的解分别提供了问题式(15)的上界和下界,通过迭代求得的上界序列和下界序列收敛的同一点即为全局最优解.由图 8可见,上界序列和下界序列在迭代约43次后收敛于一点.因算法是运行在中央服务器上,一般有较充足的计算资源,该迭代次数完全可以满足实际应用对实时性的要求.
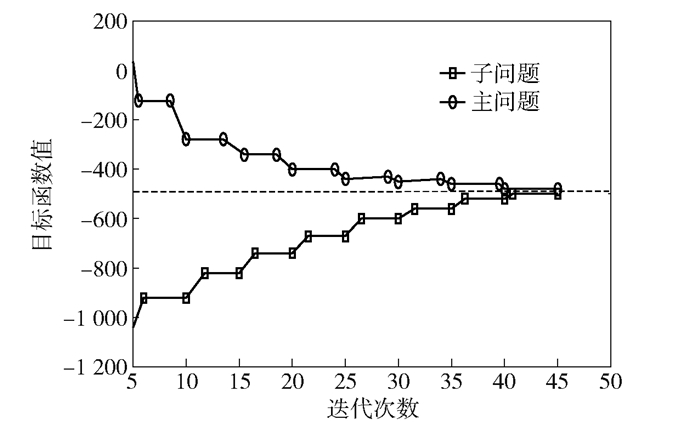
|
图 8 算法收敛性能 |
读写器间干扰是制约多读写器应用系统性能的主要因素,现有的算法仅单一地考虑接入时间或功率控制的优化,难以适应不同的读写器密度.笔者提出的基于功率调整与随机接入联合优化的RFID多读写器抗干扰算法,可以充分发挥功率控制和接入时间控制的优势,在读写器密度大范围变化时均能做出良好的优化,有效提高了标签识别率.同时,采用广义Benders方法对算法进行了主问题和子问题分解,降低了算法复杂度,提高了算法的实用性.通过仿真验证,所提算法在标签识别率和数据吞吐量等方面均优于现有算法,且具有良好的公平性和收敛性能.后续工作将研究通过分布式算法进一步提高算法的实时性能.
| [1] |
Rezaie H, Golsorkhta M. A fair reader collision avoidance protocol for RFID dense reader environments[J]. Wireless Networks, 2017, 24(1): 1-12. |
| [2] |
Zhang Shigeng, Jiang Danming. A high throughput reader scheduling algorithm for large RFID systems in smart environments[C]//IEEE International Conference on Smart Computing. Hong Kong: IEEE Press, 2017: 1-8.
|
| [3] |
Ferrero R, Gandino F. Improving colorwave with the probabilistic approach for reader-to-reader anti-collision TDMA protocols[J]. Computers in Industry, 2018, 20(3): 183-192. |
| [4] |
Mitton N, Mbacke A. Distributed efficient & fair anticollision for RFID protocol[C]//IEEE 12th International Conference on Wireless and Mobile Computing. New York: IEEE Press, 2016: 1-8.
|
| [5] |
Amadou I, Mitton N. High adaptive MAC protocol for dense RFID reader-to-reader networks[C]//Ad Hoc Networks 7th International Conference. San Remo: IEEE Press, 2015: 82-93.
|
| [6] |
Vales A, Parrado G. OSL:an optimization-based scheduler for RFID dense-reader environments[J]. Ad Hoc Networks, 2016, 37(2): 512-525. |
| [7] |
Kim Doyun, Yoon Hyungoo, Jang Byungjun. Effects of reader-to-reader interference on the UHF RFID interrogation range[J]. IEEE Transactions on Industrial Electronics, 2009, 56(7): 2337-2346. DOI:10.1109/TIE.2009.2012451 |
| [8] |
Wang Youchiun, Liu Shuju. Minimum-cost deployment of adjustable readers to provide complete coverage of tags in RFID systems[J]. Journal of Systems and Software, 2017, 134(12): 228-241. |
| [9] |
Long Jing, Li Jiancheng. An adaptive power control algorithm in RFID systems[C]//The 4th International Conference on Intelligent System and Applied Material. Taiyuan: Trans Tech Publications Ltd, 2014: 1726-1729.
|
| [10] |
Wu Liming, Chen Taiwai, Xiang Ying. RFID anti-collision for internet of things based on power control and backoff algorithm[J]. International Journal of Advancements in Computing Technology, 2012, 4(22): 560-566. DOI:10.4156/ijact.vol4.issue22.63 |
| [11] |
EPCglobal. Class 1 generation 2 UHF air interface protocol standard v. 1.1. 0[EB/OL]. (2009-05-26)[2018-06-10]. http://www.epcglobalinc.org/standards/uhfc1g2.
|
| [12] |
Mo J, Warland J. Fair end-to-end window-based congestion control[J]. IEEE/ACM Trans Networking, 2000, 8(1): 556-567. |
| [13] |
Floudas C. Nonlinear and mixed-integer optimization:fundamentals and applications[M]. Oxford: Oxford Univ Press, 1995: 114-143.
|
| [14] |
陈宝林. 最优化理论与算法[M]. 北京: 清华大学出版社, 2005: 436-439.
|
| [15] |
Boyd S, Vandenberghe L. Convex optimization[M]. Cambridge: Cambridge University Press, 2004: 225.
|


