2. 携程(上海)计算机技术有限公司, 上海 200233
业务流程预测性监控是过程管理的重要内容,已有的研究大部分是基于显式的工作流模型进行预测.但是在实际应用中,企业可能并没有对整个过程实施端到端的工作流建模和管理,或者由于权限原因只能够获得部分执行日志,难以基于完整的业务流程模型进行预测,对此,提出了一种基于频繁活动集的序列编码处理日志中的低频活动,并通过搜寻历史相似数据进行预测的方法.该方法能够随着日志的更新适应由于概念漂移导致的模型改变.在真实的数据集上进行的实验结果验证了算法的有效性.
2. Ctrip Computer Technology(Shanghai) Company Limited, Shanghai 200233, China
The problem of predicting an ongoing business process based on sequence is discussed. Business process predictive monitoring is an important part of process mining. Most of the existing research focuses on forecasting based on explicit workflow models. However, the enterprise may not implement end-to-end workflow modeling and management for the process, or only own partial execution logs due to permissions. In these cases, it is difficult to make prediction based on the complete process model. This article proposes a frequent activity set based sequence encoding method to handle the low-frequency activities in the log, and performs prediction by searching historical similar data. As the log is updated, the algorithm will adapt to model changes due to the concept drift. The algorithm is validated on real data sets.
目前企业的业务流程大多通过信息化的手段进行管理.在业务流程执行时,会将其执行过程记录成事件日志.通过对事件日志进行挖掘分析,可以对执行中的流程进行预测性监控.预测性监控可以帮助企业监控每个流程执行的情况,并及时发现风险,以提早做出相应对策,提高企业调度资源的能力.如果业务过程的模型已知或可以被挖掘,可以模型为基础,通过数据分析来对流程时间进行预测.在此前的研究中,众多研究者基于平稳业务过程的假设提出了一些基于过程模型的预测方法.然而在实际情况下,预测无法以已知的流程模型为基础.导致无法得知流程模型的原因有2部分,一是信息不充分导致的模型未知;二是业务流程的复杂性导致流程模型难以被挖掘.
首先,由于种种因素,企业往往没有对端到端的完整流程进行建模,并通过工作流系统进行管理,使得某些环节并不在工作流系统的管控之下.在另外一些场景中,外部需要知道或者预测流程的进展情况,出于数据隐私保护的原因,此时他们只能够得到某些事件发生的信息,而并不能知道整个过程的所有活动及活动间的关系.在这些情况下,难以得知流程的模型.
其次,每个流程的特殊性以及外部环境的多变性也为流程时间预测带来了进一步的挑战.业务流程的复杂性表现在:随着时间的推移,流程可能发生改变;并行执行的活动在活动序列中表现为无序的穿插;在日志中存在大量出现的历史数据过少的低频活动.业务流程的复杂性不仅仅导致活动间的关系无法挖掘,也导致了模型未知的预测性监控方法效果不佳.
为了解决现实中过程执行形成的复杂事件日志的时间预测性监控问题,笔者提出了一种基于频繁活动集序列编码的时间预测性监控方法.在无法得知流程模型的基础上,该方法解决了事件日志中概念漂移、低频活动、并行活动等问题,并通过计算活动的频繁模式,对于事件序列进行编码;随后考虑了不同属性和活动对于预测目标的影响力,对序列间距离进行衡量;最后寻找历史中相似序列,对当前活动持续时间及下一活动进行预测.
1 相关工作预测性业务流程监控可以根据是否需要过程模型分为两大类.一部分研究者侧重于挖掘过程模型后进行预测性监控. Rogge-Solti等[1-2]通过考虑活动持续时间之间的相关性,构建了Petri网预测过程的剩余执行时间模型;使用一种随机Petri网的方法,从事件数据中提取信息构建概率模型,并计算违反时间限制的风险. Ghattas等[3]采取决策树的方法,通过历史数据中上下文信息挖掘路径决策和流程结果之间的关系,推导出决策标准,预测剩余执行时间以及其他特征. Lakshmanan等[4]提出了一种特定概率过程模型,用于预测未来活动的可能性.研究还表明,在特定条件下,该模型是马尔可夫模型. Maggi[5]和Burattin等[6]则提出了一种更为快速的在线流式预测算法,将发现的过程模型用过程建模语言表示,并使用基于滑动窗口和有损计数的挖掘方法.
大部分研究者基于已知的过程模型或者根据日志构建出过程模型后进行预测性监控.但在过程模型未知情况下,根据日志准确复现过程模型是理论上的.在实际中,由于日志存在大量低频、异常活动,并且过程随着时间变化、外部环境因素变化发生概念漂移,在这种情况下,建立过程模型会导致较大误差.
另一类监控性预测则放宽了假设,不需要得到过程模型而仅仅基于日志进行预测.这种预测方式是通过日志中活动的执行序列进行预测的.基于活动序列的预测中,序列编码是其中重要的一部分.序列编码方法包括布尔编码、频率编码以及基于索引编码等方法. Leontjeva等[7]提出了一种基于隐马尔可夫模型的复杂序列编码方法,并对比了多种活动编码算法在支持向量机下对未来执行活动进行预测的效果. Tax等[8]提出了一种在基于频率编码的基础上使用长短期记忆神经网络对下一活动及剩余执行时间进行预测的算法. Polato等[9]在基于控制流视角的布尔编码基础上添加了对时间以及数据属性的编码,利用支持向量回归进行剩余时间预测. Le等[10]则使用相似序列片段对比技术,提出了一种新的基于K近邻的预测方法,对流程异常进行预测,但目前已有的研究对低频活动和并行活动并没有做相应处理.
2 基本概念 2.1 算法基础概念定义1 事件活动.设
定义2 日志轨迹. E′为E中活动的所有子序列集合,σ∈E′,表示为σ=〈e1, e2, …〉是一条日志轨迹.
定义3 事件日志.一个事件日志G={σ1, σ2, …}是多条日志轨迹的集合.
定义4 前缀轨迹.对日志轨迹σ=〈e1, e2, …, en〉而言,其k前缀轨迹为
| $ {{\sigma '}_k} = \left\langle {{e_1},{e_2}, \cdots ,{e_k}} \right\rangle ,\;\;\;\;0 < k < n $ | (1) |
在日志中,每个事件均关联一些属性,需要定义函数将这些属性映射到轨迹中.
定义5 事件属性分配函数.定义事件属性集合A={A1, A2, …, Ap},Ai代表该属性的值域,则分配函数πAi有映射E→Ai.对事件e而言,πAi(e)=aji (aji∈Ai).
以活动为例,假设事件e属于活动αj,则有
| $ {\pi _\mathscr{A}}\left( e \right) = {\alpha _j} $ | (2) |
在实际的日志中,属性不仅仅与事件相关,也有部分属性与整个日志轨迹相关.
定义6 日志相关属性.若属性与每一条日志轨迹σ相关联,则称为日志相关属性B.定义分配函数CBi(σ)=bji(bji∈Bi).所有的日志相关属性可以构成特征向量g,其中gi=CBi(σ)=bji.
2.2 基线编码方法下面介绍一些常用的事件序列编码方法.
定义7 布尔编码.假设属性Ai有v种不同值{a1i, a2i, …, avi},对于事件前缀序列σ′k=〈e1, e2, …, ek〉,定义布尔编码为
| $ B\left( {{{\sigma '}_k},a_j^i} \right) = \left\{ {\begin{array}{*{20}{l}} {1,}&{\exists e \in {{\sigma '}_k},{\pi _{{A_i}}}\left( e \right) = a_j^i}\\ {0,}&{其他} \end{array}} \right. $ | (3) |
用布尔编码可以构造在属性Ai上事件前缀序列σ′k的特征向量fi=(f1i, f2i, …, fvi),其中fji=B(σ′k, aji).
布尔编码将每一属性值作为特征的一维进行编码,其值意味该属性值是否在日志轨迹中出现.
基于频率的编码与布尔编码构造了相同维度的特征向量,但不同的是,其值代表该属性值在日志轨迹中出现的次数.
定义8 基于频率的编码.假设属性Ai有v种不同值{a1i, a2i, …, avi},对于事件前缀序列σ′k=〈e1, e2, …, ek〉,定义在某一属性值aji上事件序列σ′k的事件子集为
| $ E'\left( {{{\sigma '}_k},a_j^i} \right) = \left\{ {e|e \in {{\sigma '}_k},{\pi _{{A_i}}}\left( e \right) = a_j^i} \right\} $ | (4) |
定义基于频率的编码为
| $ \mathscr{F}\left( {{{\sigma '}_k},a_j^i} \right) = \left| {E'\left( {{{\sigma '}_k},a_j^i} \right)} \right| $ | (5) |
基于频率的编码可以构造在属性Ai上事件前缀序列σ′k的特征向量fi=(f1i, f2i, …, fvi),其中fji=
布尔编码和基于频率的编码只能对离散属性进行编码,而不能对连续属性进行编码.
另一类编码的方法是基于索引的编码.布尔编码和基于频率的编码方法无法体现活动发生的先后顺序,而基于索引的编码中,每个特征对应了序列中的一个位置.
定义9 基于索引的编码.假设属性Ai有v种不同值{a1i, a2i, …, avi},对于事件前缀序列σ′k=〈e1, e2, …, ek〉,定义属性Ai上事件ej基于索引的编码为
| $ \mathscr{T}\left( {{e_j},{A_i}} \right) = {\pi _{{A_i}}}\left( {{e_j}} \right)\left( {{e_j} \in {{\sigma '}_k}} \right) $ | (6) |
对于事件前缀序列σ′k而言,基于索引的编码可以构造属性Ai的特征向量fi=(f1i, f2i, …, fki),其中fji=
算法分为以下几个模块:历史轨迹编码、属性特征选择、轨迹过滤、属性特征距离衡量和检测过程变化. 图 1描述了这些模块间的关系.

|
图 1 算法框架 |
在实际情况中,模型可能存在大量低频活动,如果将所有事件日志中出现频率低于1%的活动称为低频活动,则在数据集BPI Challenge 2015[11]上,289种不同活动中低频活动占87%以上;在过程数据集BPI Challenge 2018[12]上,170个活动中低频活动约占65%.
综上,笔者提出了一种基于频繁活动集的编码方法,保留关键活动的顺序信息,并合理地处理低频活动以及并行活动.
定义10 对于活动αi、αj,它们的互信息定义为
| $ I\left( {{\alpha _i}:{\alpha _j}} \right) = \lg \frac{{p\left( {{\alpha _i},{\alpha _j}} \right)}}{{p\left( {{\alpha _i}} \right)p\left( {{\alpha _j}} \right)}} $ | (7) |
其中:p(αi, αj)为活动αi、αj在同一条日志轨迹中出现且αi出现在αj前的概率,p(αi)、p(αj)为出现的独立概率.
互信息公式体现了活动之间关系的紧密程度. I(αi:αj)越大,则认为αi、αj间紧密程度较高.
在互信息公式的基础之上,定义频繁活动集lk.
定义11 频繁活动集.设lk是一个频繁活动集,则αi, αj∈lk,都存在I(αi:αj)≫0.
通过计算所有活动之间的互信息,可以得到活动间是否属于同一频繁活动集.然而,暴力搜索得到频繁活动集的方法开销太大,因此借鉴数据挖掘中Apriori算法的思想来生成频繁活动集. Apriori算法中,利用最小支持度作为关联规则,而笔者使用了互信息公式作为频繁活动集的判断规则,该规则在活动先后顺序关系发生改变时,关联关系也会发生改变.
设lu表示具有u个活动的频繁活动集合,Lu={lu, 1, lu, 2, …}表示所有包含u个活动的频繁活动集合lu的集合.对∀lu, x∈Lu,集合内活动表示为lu, x={αx, 1, αx, 2, …, αx, u}.
由定义11可知,如果l是一个频繁活动集,则它的所有子集也是频繁活动集.如果l不是一个频繁活动集,则它的所有超集也不是频繁活动集.在已知Lu的情况下,期望生成下一层集合Lu+1.首先对于lu, x∈Lu,可以找到所有满足下列条件的lu, y:
| $ \forall z \in \left[ {1,u - 1} \right]\;有\;{\alpha _{x,z + 1}} = {\alpha _{y,z}} $ | (8) |
式(8)表明,lu, y是前u-1个活动与lu, x中后u-1个活动完全相等的频繁子集.在此基础之上,将候选子集cu+1加入候选集Cu+1.其中
| $ {c_{u + 1}} = {l_{u,x}} \cup \left\{ {{\alpha _{y,u}}} \right\} $ | (9) |
在Lu中,将所有满足式(9)要求的集合对〈lu, x, lu, y〉生成候选子集加入候选集Cu+1中.最后,对候选集Cu+1中所有的候选子集cu+1进行检查,如果cu+1满足定义11的要求,则将其加入Lu+1中.
在L1中,每个活动单独生成一个集合{α},然后两两结合,通过上述算法生成L2.之后层层递推,直到无法生成下一层L为止.
由于对每一层Lu,均排除一些非频繁子集,所以防止了搜寻空间的指数级增长.
定义12 基于频繁活动集的编码.假设活动可以分为w个频繁子活动集,其中大小为u的频繁子活动集可以表示为lu, x.对lu, x在这里重新编序为ls*,s=
对于事件前缀序列σ′k=〈e1, e2, …, ek〉,可以将其分为E*={E1*, E2*, …, Ew*}w个事件子序列.每个ls*均对应可以生成一个事件子序列Es*.
对事件ei,若πA(ei)=αj,且αj∈ls*,则ei∈Es*.
对于事件子序列Es*,可以重新表示为子事件集合{es, 1*, es, 2*, …, es, k**}.
在事件子序列集合E*基础上可以构建w个子特征向量f1*, f2*, …, fw*.对每个事件子序列Es*,在子活动集ls*=lu, x上的特征向量fs*可以表示为
| $ \mathit{\boldsymbol{f}}_s^ * = \left( {f_{s,1}^ * ,f_{s,2}^ * , \cdots ,f_{s,{k^ * }}^ * } \right) $ | (10) |
其中
| $ f_{s,i}^ * = \mathscr{T}\left( {e_{s,i}^ * ,\mathscr{A}} \right) = {\pi _A}\left( {e_{s,i}^ * } \right) $ | (11) |
所有的特征子向量可组成特征向量:
| $ {\mathit{\boldsymbol{f}}^ * } = \left( {\mathit{\boldsymbol{f}}_1^ * ,\mathit{\boldsymbol{f}}_2^ * , \cdots ,\mathit{\boldsymbol{f}}_w^ * } \right) $ | (12) |
特征向量中除了活动序列信息之外,还有其他属性信息.在使用这些特征构建特征向量之前,需要先评判出特征对预测结果的影响力.
随机森林是一种集成学习方法,可以消除冗余和不相关特征,分析特征对结果的影响.由于随机森林可以有效地处理噪声,具有将特征的重要程度进行排序的特性,这里使用随机森林对属性进行筛选.
如果将活动属性
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{X}} = \left( {f_1^ * , \cdots ,f_w^ * ,{f^1}, \cdots ,{f^{p - 1}},{g^1}, \cdots ,{g^q}} \right) = }\\ {\left( {{x_1},{x_2}, \cdots ,{x_{w + p + q - 1}}} \right)} \end{array} $ | (13) |
对于每个特征x,计算其重要度v(x).通过计算特征在随机森林中的每棵树上做出的贡献大小,得到特征的重要程度.随机森林既可以用于分类也可以用于回归.对于流程下一活动的预测是一个多分类问题,对于当前活动执行持续时间是一个回归问题.为了处理回归问题,这里选择了cart树.为了评价贡献,需要计算特征平均信息的增益大小,从而得出特征的重要程度:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{V}} = \left( {{v_1},{v_2}, \cdots ,{v_{w + p + q - 1}}} \right) = }\\ {\left( {v\left( {{x_1}} \right),v\left( {{x_2}} \right), \cdots ,v\left( {{x_{w + p + q - 1}}} \right)} \right)} \end{array} $ | (14) |
轨迹过滤模块从历史数据中提取与当前轨迹相似的轨迹前缀.轨迹前缀包含了执行的控制流信息.两条相似的轨迹更可能在未来也具有相似的执行行为.这里提取出所有以当前活动α为结尾的前缀轨迹,即对Gα={σ1, σ2, …},有
| $ \forall {\sigma _i} \in G',{\pi _A}\left( {\mathscr{J}\left( {{\sigma _i}} \right)} \right) = \alpha $ | (15) |
其中函数
在得到特征向量以及特征重要性之后,算法需要衡量轨迹间距离.对于频繁子活动特征向量,将采用编辑距离衡量特征距离.编辑距离定义为将一个序列转换为另一个序列所需的插入、删除和替换操作的最小次数.
然而,在基于索引的编码上使用编辑距离难以处理并行活动的情况.假设活动序列〈A, C〉、〈B, D〉,如图 2所示是2个并行分支,但是并行活动的执行顺序往往不相关,因此导致通过编辑距离衡量会出现较大误差.比如,序列〈A, B, C, D〉与〈B, A, D, C〉是该流程的2次不同执行,但它们之间的编辑距离为4.因此提出一种算法,对频繁子集合内部采用编辑距离衡量,并对子序列结果加权计算总距离.除此之外,本算法将根据子序列重要性程度单独对2个活动分支赋予不同权重.

|
图 2 并行活动情况示例 |
对于图 3所示的分支活动而言,有2种执行情况〈A, B, C, D〉与〈A, B, E, F〉.这里将分为2种不同的情况:第1种情况,活动分支被选择的概率相似,此时将划分为3个集合{A, B}、{C, D}以及{E, F};第2种情况,活动分支被选择的概率差异较大,〈A, B, E, F〉是一个小概率发生的分支,而〈A, B, C, D〉大概率发生,此时频繁子集合划分为{A, B, C, D}与{E},该情况下将分别计算每个集合对结果的影响程度.

|
图 3 分支活动情况示例 |
所提出的距离衡量方法如下:
设序列信息特征表示为X.对轨迹σa与σb而言,lev(x(σa), x(σb))代表轨迹σa与σb在x上的编辑距离,ρ(x(σa), x(σb))代表在x上的欧氏距离,h(x(σa), x(σb))代表在x上的海明距离.
序列信息特征对应权重为V,可得轨迹距离衡量函数:
| $ \begin{array}{*{20}{c}} {d\left( {{\sigma _a},{\sigma _b}} \right) = \sum\limits_{i = 1}^n {{v_i}} \text{lev}\left( {x\left( {{\sigma _a}} \right),x\left( {{\sigma _b}} \right)} \right) + }\\ {\sum\limits_{j = w + 1}^{w + p + q - 1} {{v_j}} d\left( {x\left( {{\sigma _a}} \right),x\left( {{\sigma _b}} \right)} \right)} \end{array} $ | (16) |
其中
| $ d\left( {x\left( {{\sigma _a}} \right),x\left( {{\sigma _b}} \right)} \right) = \left\{ {\begin{array}{*{20}{c}} {\rho \left( {x\left( {{\sigma _a}} \right),x\left( {{\sigma _b}} \right)} \right),}&{连续值}\\ {h\left( {x\left( {{\sigma _a}} \right),x\left( {{\sigma _b}} \right)} \right),}&{离散值} \end{array}} \right. $ | (17) |
在轨迹过滤模块的基础之上,利用式(17)计算距离,寻找最为相似的β条历史轨迹.对相近的β条历史轨迹中目标值投票(离散值)或求均值(连续值),得到预测结果.
3.5 概念漂移检测随着时间的推移,业务过程本身也会随之发生改变.下面将业务过程本身的改变分为2种情况.
1) 活动间频繁关系发生改变
当新的执行轨迹加入历史数据时,同步更新所有相关活动的互信息值.如果互信息值的变化导致频繁子序列的划分发生变化,则重新计算频繁活动集.
2) 活动间频繁关系未发生改变
若活动间频繁关系未发生改变,通过轨迹过滤模块和特征距离衡量模块寻找历史相似轨迹的方法具有自动过滤业务流程变更前的日志的能力,筛选出最相近的日志中事件序列进行预测.
综上,提出了一种基于频繁活动子集的编码方式,并基于该编码方式提出了一种预测算法.
4 实验下面使用真实的日志数据集BPI challenge 2018进行实验[12].该数据集描述了德国农民向欧洲农业担保基金申请补贴相关过程的执行情况.该日志中包含2015~2017年共3年43 809条执行记录.但由于法规的变化或政策实行的灵活性,每一年的流程可能会有所不同.日志中描述了每条申请过程的执行轨迹.申请轨迹本身具有一系列属性,如申请计划、申请人、执行部门等.由于超过一半以上的执行记录具有独一无二的轨迹,为预测带来了挑战.
这里将活动时长定义为活动对某资源从开始处理到结束处理所耗费的时间.实验中,所有的事件根据发生时间顺序排序.事件分为2部分:第1部分包括前80%的事件,作为训练集;剩余事件作为第2部分测试集.训练集用于寻找频繁活动子集以及为特征重要性打分.在测试时,添加当前序列发生时间点之前的所有序列进入搜寻目标历史序列的范围之内.
实验使用布尔编码、频率编码、基于索引编码作为对比算法,并且对属性值使用随机森林算法筛选,在K近邻下的表现与所提出的算法进行对比.
第1部分实验对比了各类编码算法预测当前活动执行结束之后下一个执行活动的性能.
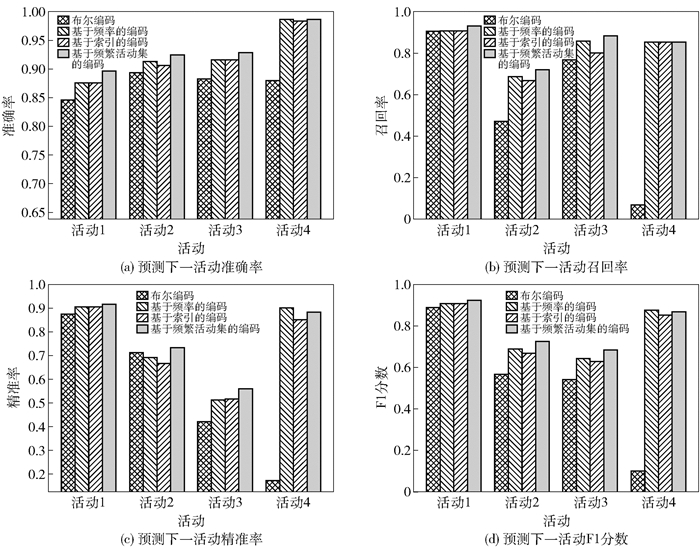
为了衡量数据集上所有活动的预测性能,这里采用了Micro-F1分数衡量.在类别分布不均匀的情况下,更合适使用Micro-F1作为衡量指标.实验中针对每个活动,使用了准确率、召回率、精准率、F1分数作为衡量标准.实验中互信息阈值为4,选择的近邻点数量为5,得到了最优的预测结果. 图 4展示了出现频率最高的4个活动的准确率、召回率、精准率和F1分数. 表 1展示了所有活动的F1分数.可以看到,所提出的算法在各个标准上均比基线算法有所提高. 表 2展示了不同的K值对于预测结果的影响,并且值为5预测效果最佳.
|
图 4 预测下一个活动性能 |
|
|
表 1 预测下一执行活动结果 |
|
|
表 2 不同近邻点数量在频繁子集编码下对预测结果的影响 |
第2部分实验对比了各类编码算法预测当前活动对资源的操作何时结束的性能.实验结果如表 3所示.
|
|
表 3 各方法预测活动持续时间结果 |
由于存在部分瞬时活动, 因此绝对误差更能反映预测的准确程度.由表 3可知, 所提出的算法同样提升了对当前活动持续时间预测的准确性.
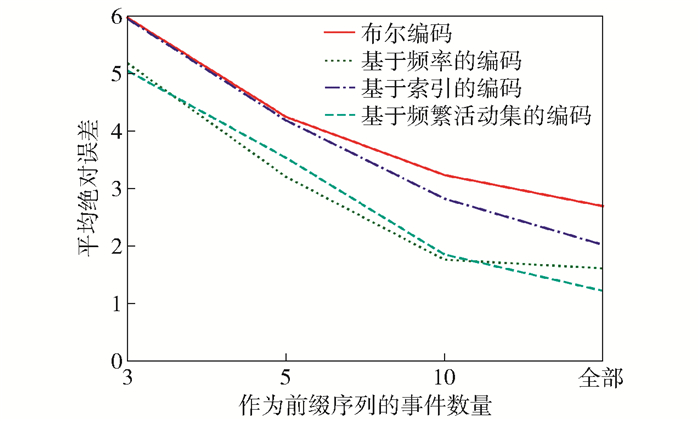
在图 5中,实验对比了选择不同数量的事件作为前缀序列预测活动持续执行时间的平均绝对误差.实验表明,选择的事件数量越多,预测效果越好.
|
图 5 预测活动持续执行时间的平均绝对误差 |
笔者提出了一种使用频繁活动子序列对控制流进行编码的方法,通过子序列的重要性程度计算序列间距离,并基于K近邻方法预测下一活动及当前活动执行时长.算法采用了真实数据集进行测试.针对数据集存在概念漂移以及大量异常活动的情况,在数据集上的测试表明,相对于布尔编码、频率编码和基于索引的方法,所提方法在预测下一活动以及活动执行时间上均有更好的性能.
| [1] |
Rogge-Solti A, Weske M. Prediction of remaining service execution time using stochastic Petri nets with arbitrary firing delays[C]//International Conference on Service-Oriented Computing. Berlin, Heidelberg: Springer, 2013: 389-403.
|
| [2] |
Rogge-Solti A, Weske M. Prediction of business process durations using non-Markovian stochastic Petri nets[J]. Information Systems, 2015, 54: 1-14. DOI:10.1016/j.is.2015.04.004 |
| [3] |
Ghattas J, Soffer P, Peleg M. Improving business process decision making based on past experience[J]. Decision Support Systems, 2014, 59: 93-107. DOI:10.1016/j.dss.2013.10.009 |
| [4] |
Lakshmanan G T, Shamsi D, Doganata Y N, et al. A markov prediction model for data-driven semi-structured business processes[J]. Knowledge and Information Systems, 2015, 42(1): 97-126. DOI:10.1007/s10115-013-0697-8 |
| [5] |
Maggi F M, Burattin A, Cimitile M, et al. Online process discovery to detect concept drifts in ltl-based declarative process models[C]//OTM Confederated International Conferences on the Move to Meaningful Internet Systems. Berlin, Heidelberg: Springer, 2013: 94-111.
|
| [6] |
Burattin A, Cimitile M, Maggi F M, et al. Online discovery of declarative process models from event streams[J]. IEEE Transactions on services computing, 2015, 8(6): 833-846. DOI:10.1109/TSC.2015.2459703 |
| [7] |
Leontjeva A, Conforti R, Di Francescomarino C, et al. Complex symbolic sequence encodings for predictive monitoring of business processes[C]//International Conference on Business Process Management. Cham: Springer, 2015: 297-313.
|
| [8] |
Tax N, Verenich I, La Rosa M, et al. Predictive business process monitoring with LSTM neural networks[C]//International Conference on Advanced Information Systems Engineering. Cham: Springer, 2017: 477-492.
|
| [9] |
Polato M, Sperduti A, Burattin A, et al. Data-aware remaining time prediction of business process instances[C]//2014 International Joint Conference on Neural Networks (IJCNN).[S. l.]: IEEE, 2014: 816-823.
|
| [10] |
Le M, Nauck D, Gabrys B, et al. Sequential approaches for predicting business process outcome and process failure warning[C]//SIMPDA. Riva del Garda, Italy: ASSERT4SOA, 2013: 1-15.
|
| [11] |
van Dongen. BPI challenge 2015 dataset[DB/OL]. (2015-05-01)[2018-07-01]. http://EindhovenUniversityofTechnology, 2015.
|
| [12] |
van Dongen. BPI challenge 2018[DB/OL]. (2018-03-13)[2018-07-01]. http://EindhovenUniversityofTechnology, 2018.
|



