2. 青岛农业大学 理学与信息科学学院, 青岛 266100;
3. 青岛理工大学 信息与控制工程学院, 青岛 266100;
4. 山东青岛烟草有限公司 综合计划处, 青岛 266100
针对特征选择过程中准确率和计算效率不平衡问题,提出了一种快速特征选择框架(FFFS).基于该框架,使用最小冗余最大相关方法(MRMR)选择候选特征,借助序列前向选择方法(SFS)验证性能,并通过限定迭代次数提高计算性能.与MRMR、SFS和混合序列浮动前向选择算法(FDHSFFS)的对比实验结果表明,提出的快速特征选择算法MRMR-SFS能在预测准确率和计算效率之间取得较好的平衡.
2. Science and Information College, Qingdao Agricultural University, Qingdao 266100, China;
3. School of Information and Control Engineering, Qingdao University of Technology, Qingdao 266100, China;
4. Comprehensive Planning Office, Shandong Qingdao Tobacco Copany Limited, Qingdao 266100, China
Aiming at the imbalance between accuracy and computational efficiency in feature selection, a fast feature selection framework (FFFS) is proposed. Based on this framework, a fast feature selection algorithm, MRMR-SFS, is proposed. The minimum redundancy maximum relevance (MRMR) method is used to select the candidate features, and sequential forward selection (SFS) method is used to verify the performance of the candidate features as well. It improves the calculation efficiency by limiting the number of iterations. Comparison experiments with the MRMR, SFS and a filter-dominating hybrid sequential floating forward selection algorithms demonstrate that MRMR-SFS can balance the accuracy and computational efficiency well.
随着数据量的增加,数据中充斥的噪声和冗余也日益增加.由于特征选择具有良好的去冗余和噪声能力,已成为数据挖掘中非常重要的预处理步骤.通过去除无关和冗余特征,一个好的特征选择算法不仅能显著降低特征维数,而且能提高预测性能,增强对数据的理解[1-2].
特征选择算法通常可以分为filter方法[3]、wrapper方法[4]和hybrid方法[5]三大类. filter方法与学习算法无关,运行效率高,但难以发现特征间潜在的相关性,故选出的特征子集往往不理想. wrapper方法将学习算法作为内嵌函数,以其准确率作为选择特征的标准,通常能发现特征间潜在的相关性,选出的特征子集往往具有良好的性能,但由于搜索空间大,且需要学习算法的介入,计算量太大,尤其是随着特征维数和样本数的增加,效率太低,甚至不可接受. hybrid方法虽然结合了filter方法的高效率和wrapper方法的高准确率特点,但也会受限于filter方法和wrapper方法的缺陷,难以真正解决计算效率和准确率之间的平衡问题.
基于以上原因,笔者提出了一种快速的特征选择框架(FFFS,a fast feature selection framework),并基于该框架提出了一种特征选择算法MRMR-SFS(minimum redundancy maximum relevance-sequential forward selection).该算法使用Pearson相关系数[6]计算特征相关性,使用MRMR方法选择候选特征,借助SFS方法验证候选特征性能,并限制了算法的迭代次数.与当前主流算法的对比实验验证了MRMR-SFS算法的性能.
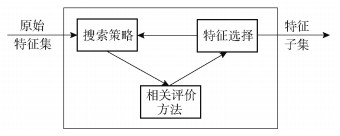
1 FFFS特征选择框架 1.1 现有特征选择框架目前存在2种主要评价相关特征的框架:对单个特征的评价和特征子集评价.单个特征的评价框架如图 1所示.
|
图 1 单个特征的评价框架 |
单个特征评价常用于filter方法.通常先使用相关评价方法评价单个特征和预测值(类标)之间的相关性,并根据相关性排序,保留与预测值(类标)相关性强的特征组成特征子集,再选择合适的搜索策略搜索特征,结合相关评价方法,如互信息和相关系数,去除冗余特征,最后选择的特征子集中的特征与预测值(类标)之间的相关性强,且没有冗余.单个特征评价的计算量通常为O(n)或者O(n2),其中n为特征维数,适合高维数据的处理,但该方法产生的结果往往与最优结果相差较远.
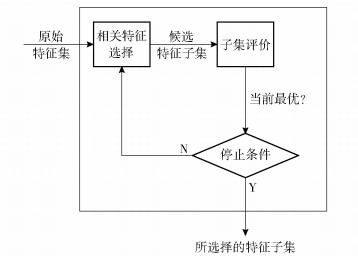
很多特征选择方法通过评价特征子集来处理特征相关,特征选择框架如图 2所示.通过搜索策略产生候选特征子集,使用评价函数评价产生候选特征子集的性能,并与之前使用此评价函数评价的性能最好的一组进行比较.如果新的候选特征子集的性能更优,则替代之前的子集成为当前候选特征子集,产生、评价候选特征子集的过程不断循环,直到满足给定的停止条件为止.该方法已被证明能产生较好的结果[1, 7],但在候选特征子集产生和评价阶段的计算量太大,候选特征子集的数量最多可以达到2n个,学习算法的评价次数最高也可达到2n次.若数据的维数很高,其计算量是巨大的.
|
图 2 特征子集的评价框架 |
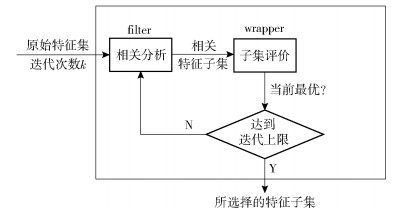
基于1.1节所述2种特征选择框架,笔者提出了一种新的快速的hybrid特征选择框架FFFS.该框架结合了单个特征评价和特征子集评价2种评价标准,通过限制迭代次数,克服了单个特征评价的低准确率和特征子集评价的低效率. FFFS特征选择框架如图 3所示,其中,限制迭代次数为k.
|
图 3 FFFS特征选择框架 |
FFFS特征选择框架分2部分:filter过程和wrapper过程.
1) filter过程:对单个特征进行评价,使用filter方法选出当前特征子集中的最优特征Fbest,添加到当前特征子集S,构成S′.
2) wrapper过程:对特征子集进行评价,使用学习算法评价S′的性能,若其性能优于S的性能,则把特征子集S′设为当前特征子集.
filter-wrapper过程迭代k次,得到的特征子集即为近似最优特征子集.
FFFS特征选择框架的优势为:①使用filter方法选择相关特征,降低了计算量;②由于filter方法和wrapper方法交叉进行,避免了先使用filter方法移除无关或冗余特征带来的准确率下降;③设置了迭代次数上限,在保证预测准确率的同时进一步降低了计算效率.基于以上框架,笔者提出了一种hybrid特征选择算法MRMR-SFS.
2 MRMR-SFS算法MRMR-SFS算法既适应于离散数据,也适应于连续数据,笔者仅针对连续数据给出了相关分析,离散数据的相关分析类似,只是选择的相关评价标准有所差异.实验采用的相关评价标准为Pearson相关系数.
2.1 特征相关分析在分析特征相关之前,首先区分2种相关性:F-相关和Y-相关. F-相关指2个特征Fi和Fj之间的相关性,用ρi, j表示;Y-相关指特征Fi和预测值y之间的相关性,用ρi, y表示.
MRMR-SFS算法相关特征的选择采用最大相关最小冗余思想,即在原始特征空间中寻找Y-相关最大而F-相关最小的子集. M表示原始特征空间,n表示原始特征空间的维数,S表示当前选择的特征子集,MS=M-S为剩余特征组成的集合.最大相关条件通过式(1)描述:
| $ \max R_{V}, R_{V}=\frac{1}{|S|} \sum\limits_{F_{i} \in S} \rho_{i, y} $ | (1) |
最小冗余条件通过式(2)描述:
| $ \min R_{D}, R_{D}=\frac{1}{|S|^{2}} \sum\limits_{F_{i}, F_{j} \in S} \rho_{i, j} $ | (2) |
寻找的最优特征子集要同时满足条件(1)和条件(2),若要同时优化条件(1)和条件(2),需要把它们联合起来.但由于寻求最优特征子集的计算量太大[8],故退而寻求近似最优特征子集.寻求近似最优特征的标准记为PCCQ(pearson correlation coefficient quotient criterion),有
| $ \max \limits_{F_{i} \in M_{S}}\left(\frac{\rho_{i, y}}{\frac{1}{|S|} \sum\limits_{F_{j} \in S} \rho_{i, j}}\right) $ | (3) |
MRMR-SFS算法首先使用PCCQ标准选出候选特征,然后使用学习算法验证增加此候选特征能否提高预测性能.虽然通过这种方法选择的特征子集不一定是最优的,但是子集中的特征均能提高预测性能,保证了预测准确率.
2.2 算法描述为进一步降低计算量,MRMR-SFS算法限定迭代次数为k.算法从空集开始,迭代k次,产生最终的近似最优特征子集S.具体过程见算法1.其中:J为性能评价函数,Fbest表示使用最大相关最小冗余思想选出的近似最优候选特征.
算法1 MRMR-SFS算法
输入: M(F1, F2, …, Fn, Y) //数据集M
k //迭代次数
输出: S
1 begin
2 for i=1 to n do begin
3 对数据集M中的每个特征Fi计算ρi, y;
4 end
5 Fj=Max(M); //选择第一个特征
6 S={Fj};
7 MS=M-S;
8计算当前特征子集S的性能,记为J(S);
9 for p=1 to k do begin
10 for i=1 to |Ms|
11
12 end
13 获取最大PCCQ(i)值对应的特征Fbest;
14 If (J(S∪{Fbest})>J(S))
15 S=S ∪{Fbest};
16 end
17 MS=MS-{Fbest};
18 end
19 输出S;
20 end
第1个特征的选取过程(第2~6行)如下:获取M中ρi, y值最大的特征Fj作为集合S中的第1个特征,把Fj添加到集合S,同时从集合M中移除Fj,并计算特征子集S的性能,记为J(S).
第j(j≥2)个特征的选取过程如下:计算MS中每个特征Fi的PCCQ(i)值,从计算结果中选择最大的PCCQ(i)值,最大PCCQ(i)值对应的特征记为Fbest(第10~13行).用学习算法计算添加Fbest到当前特征子集S后的性能,若J(S∪{Fbest})>J(S),说明增加Fbest到当前特征子集后性能提高,则更新S=S∪{Fbest}.以上过程迭代k次,最后输出近似最优特征子集S.
MRMR-SFS算法的计算量主要由2部分组成:基于最大相关最小冗余思想筛选候选特征产生的计算量;学习算法验证特征子集性能产生的计算量.前者的计算量主要集中在F-相关值的计算上,算法的计算量与n2成正比,为O(kn2).因为每筛选出一个候选特征都要使用学习算法验证添加此候选特征到当前特征子集后的性能,共筛选k次,所以后者产生的计算量为O(kA),其中,A为单次学习算法性能验证的计算量.
3 实验和分析实验使用3个基准数据集和1个真实数据集来分析MRMR-SFS算法相比于其他特征选择算法的优点和不足.
3.1 数据集实验使用数据集见表 1.
|
|
表 1 实验数据集信息描述 |
基准数据集来自UCI机器学习库.其中,Student Performance简写为SP,Communities and Crime简写为CC,UJIndoorLoc简写为UJIL.特征集SP和CC中的文本数据都已处理为数值数据.耗电量(energy consumption)数据集来自某公司一年的耗电量测试数据,简写为EC.
3.2 评价方法和标准实验使用的评价标准如下:
1) 所选择的特征维数;
2) 不同特征选择算法运行的时间;
3) 不同特征选择算法的预测误差.
实验使用相对误差来评价所选择的特征子集的性能,相对误差能很好地反映预测的可信程度,计算公式为
| $ R = \frac{1}{m}\sum\limits_{i = 1}^m {\frac{{\left| {{y_i} - {{\hat y}_i}} \right|}}{{\left| {{y_i}} \right|}}} $ | (4) |
其中:yi为实际值,
MRMR-SFS算法分别与filter方法、wrapper方法和hybrid方法(对应3种不同的特征选择框架)做了比较. MRMR方法是filter方法中最具代表性的算法之一,SFS方法是wrapper方法中的经典算法,FDHSFFS是hybrid方法中的典型算法.因此,将本文算法分别与以上3种算法进行了对比实验.经证明,MRMR算法使用除法结合方式得到的特征子集性能更优[8].因此,filter方法选择的是MRMR算法的除法结合方式,记为MRMRQ.所有算法都使用Pearson相关系数判定相关特征.
所有算法的运行环境为Intel(R) Core(TM) i5-4200U,8GB内存,Matlab 2016.
3.3 实验结果与分析实验中,MRMR-SFS算法使用多项式和局部加权线性回归算法(LWLR, locally weighted linear regression)作为特征子集的评价函数,采用10折交叉验证训练参数,留一交叉验证(LOOCV, leave one out cross validation)计算测试误差,取5次运行结果的平均值.
1) 低维数据集实验结果和分析
针对低维数据集EC和SP,由于运行时间短,计算效率可以忽略,最重要的是误差,所以本文算法主要与MRMRQ、FDHSFFS、SFS比较预测误差.
EC数据集上的实验结果见表 2.实验中,MRMR-SFS的迭代上限k设置为6,FDHSFFS所选择的特征维数上限为4.第1列的算法模型中,MRMR-SFS-P表示MRMR-SFS中的性能评价算法使用的是多项式算法,MRMR-SFS-L表示MRMR-SFS中的性能评价算法使用的是LWLR算法,以此类推.第2列显示了不同算法所选择的特征子集的平均维数和标准差,第3列显示了不同特征选择算法的运行时间和标准差,第4列显示了LOOCV预测误差和标准差.
|
|
表 2 EC数据集上的实验结果 |
可以看出,所有的特征选择算法都有很好的降维效果,且选出的特征子集的维数近似.由于EC数据集的维数和样本数都较少,所以,运行时间差距不是很大.针对EC数据集,无论使用多项式算法还是LWLR算法,本文算法的误差和SFS算法相近,均低于FDHSFFS算法,明显低于MRMRQ算法,相差分别为3.7%(多项式算法)和3.6%(LWLR).
数据集SP上的实验结果见表 3.实验中,MRMR-SFS的迭代上限k设置为6,FDHSFFS所选择的特征维数上限为4.
|
|
表 3 数据集SP上的实验结果 |
可以看出,不同算法选出的特征维数近似.由于MRMRQ没有验证算法的介入,所以运行时间最短,其次是MRMR-SFS、FDHSFFS和SFS算法. MRMR-SFS算法虽然限制了迭代次数,预测误差却与FDHSFFS和SFS近似,均略低于MRMRQ算法.
2) 高维数据集实验结果和分析
针对高维数据集CC和UJIL,在保证低预测误差的同时要保证高计算效率.因此,本文算法分别与MRMRQ、FDHSFFS、SFS在预测误差和计算效率2方面进行对比实验.
数据集CC上的实验结果见表 4.实验中,MRMR-SFS的迭代上限k设置为10,FDHSFFS所选择的特征维数上限为10.可以看出,所有特征选择算法都取得了很好的降维效果,MRMRQ的降维效果最好.随着特征维数的增加,MRMR-SFS的计算效率凸显,针对多项式算法(LWLR算法),FDHSFFS和SFS的运行时间分别为MRMR-SFS的15倍(4倍)和76倍(71倍).由于MRMRQ算法中没有学习算法的介入,所以其运行效率最高,也正因为此,其误差最大,比MRMR-SFS高16.39%(多项式算法)和16.41%(LWLR算法),其他算法的误差近似.
|
|
表 4 数据集CC上的实验结果 |
数据集UJIL上的实验结果见表 5.实验中,MRMR-SFS的迭代上限k设置为10(多项式算法)和4(LWLR算法),FDHSFFS所选择的特征维数上限为10(多项式算法)和4(LWLR算法).由于数据集UJIL维数和样本数都较高,SFS算法使用多项式作为评价函数时的运行时间已经超过288000s,故未进行SFS实验.在使用LWLR作为评价函数的特征选择过程中,由于算法的运行时间过长,所有算法只取了10折交叉验证运行一次的误差进行性能比较.
|
|
表 5 数据集UJIL上的实验结果 |
由表 5可以看出,MRMR-SFS的降维效果与MRMRQ近似,其次是FDHSFFS算法.本文算法的误差稍低于其他算法,相差不大,但计算效率远远高于SFS和FDHSFFS算法.
综上分析,不同特征选择算法在4个数据集上选择的特征子集的维数近似.特征维数较低时(n < 30),运行时间差别不大(EC和SP数据集),但维数越高,MRMR-SFS相对于FDHSFFS和SFS算法的计算优势越明显.例如,UJIL数据集上,FDHSFFS和SFS多项式算法的运行时间分别为MRMR-SFS的23倍和1548倍(SFS的运行时间按照288000s估算,实际运行时间还要长).尽管如此,MRMR-SFS得到的误差却与FDHSFFS、SFS算法近似,甚至更低.
由于MRMRQ没有学习算法的介入,其计算效率始终是最优的,正因为如此,其在EC和CC数据集上的误差很大,与最低值的差值最高为16.41%,预测效果很不稳定.而MRMR-SFS算法的误差或者是最低的,或者和最低值相近,预测性能与MRMRQ相比更稳定.
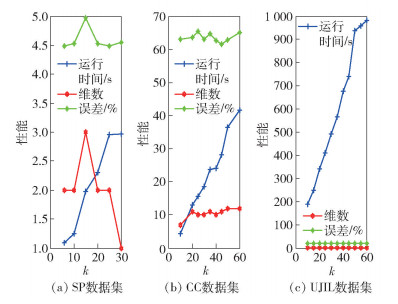
3.4 迭代次数对性能的影响MRMR-SFS算法的迭代上限设置为k,即MRMR-SFS所选择特征子集的维数不会超过k.不同的数据集,k值不同,MRMR-SFS选出的特征子集就可能不同,运行时间和误差就会有差异.在数据集SP、CC和UJIL上分别验证了MRMR-SFS-P的k值变化对性能的影响,如图 4所示.其中,SP数据集k取值上限为30,CC和UJIL数据集k取值上限为60.
|
图 4 迭代次数对MRMR-SFS算法性能的影响 |
由图 4可以看出,随着迭代次数k的增加,算法运行时间呈缓慢上升趋势,但所选特征子集的维数并没有随着k值的增加而呈上升趋势,平均误差也没有随着k值的增加而呈下降趋势.实验刚开始时,MRMR-SFS-P所选择特征子集的维数呈上升趋势,随后趋于稳定,这是由于近似最优特征子集的维数是比较稳定的.实验刚开始时,平均误差有所上升,随着维数的增加,可能会选择出更优的特征组合,因此误差趋于稳定,仅有较小的波动.
综上分析,迭代次数k并不是越大越好,MRMR-SFS算法能在较少的迭代次数(以上4个数据集实验过程中选择的k值为k=n×0.2,其中,n为原始特征集的维数)内选择出近似最优特征子集. k值的选择可根据经验,或者经过多次尝试取误差最小时对应的k值.
4 结束语分析了目前常用的3类特征选择算法的优点和不足,提出了一种快速特征选择框架FFFS,基于该框架,提出了一种MRMR-SFS特征选择算法,该算法使用MRMR方法选择候选特征,借助SFS方法验证特征的性能,并限制了算法的迭代次数. 4个数据集上的实验结果表明,与SFS、FDHSFFS算法相比,MRMR-SFS算法的性能更优,而与MRMRQ算法相比,由于MRMR-SFS在特征选择过程中有学习算法的介入,其计算效率低于MRMRQ,也正因为如此,其预测准确率在某些数据集上远高于MRMRQ,最大相差16.41%,具有更稳定的预测性能.简单快速地确定k值是下一步的研究方向.
| [1] |
Koller D, Sahami M.Toward optimal feature selection[C]//Proceedings of the 13th International Conference on Machine Learning.San Francisco: Morgan Kaufmann, 1996: 284-292.
|
| [2] |
Ahmad A, Dey L. A feature selection technique for classificatory analysis[J]. Pattern Recognition Letters, 2005, 26(1): 43-56. |
| [3] |
Yu Lei, Liu Huan. Efficient feature selection via analysis of relevance and redundancy[J]. Journal of Machine Learning Research, 2004(5): 1205-1224. |
| [4] |
Marill T, Green D. On the effectiveness of receptors in recognition systems[J]. IEEE Transactions on Information Theory, 1963, 9(1): 11-17. DOI:10.1109/TIT.1963.1057810 |
| [5] |
El Akadi A, Amine A, El Ouardighi A, et al. A two-stage gene selection scheme utilizing MRMR filter and GA wrapper[J]. Knowledge and Information Systems, 2011, 26(3): 487-500. |
| [6] |
Kohavi R, John G H. Wrappers for feature subset selection[J]. Artificial Intelligence, 1997, 97(1-2): 273-324. DOI:10.1016/S0004-3702(97)00043-X |
| [7] |
崔鸿雁, 徐帅, 张利锋, 等. 机器学习中的特征选择方法研究及展望[J]. 北京邮电大学学报, 2018, 41(1): 1-12. Cui Hongyan, Xu Shuai, Zhang Lifeng, et al. The key techniques and future vision of feature selection in machine learning[J]. Journal of Beijing University of Posts and Telecommunications, 2018, 41(1): 1-12. DOI:10.3969/j.issn.1008-7729.2018.01.001 |
| [8] |
Ding C, Peng Hanchuan. Minimum redundancy feature selection from microarray gene expression data[J]. Journal of Bioinformatics and Computational Biology, 2005, 3(2): 185-205. DOI:10.1142/S0219720005001004 |


