2. 北京邮电大学 智能通信软件与多媒体北京市重点实验室, 北京 100876;
3. 北京邮电大学 计算机学院, 北京 100876
针对一般稀疏矩阵-矩阵乘法(SpGEMM)的性能问题,提出了一种基于任务分类和低延迟散列表的图形处理器上的加速SpGEMM算法RBSPARSE.该算法由一种低成本子任务复杂度预分析方法和一种低延迟共享内存上的散列表的方法组成,以达到最大效率.通过解决负载均衡和内存延迟问题,RBSPARSE可以显著减少计算的总时间.比较了RBSparse和BHSparse,前者是最快的SpGEMM算法,结果表明RBSparse的性能是BHSparse的平均3.1倍,在最佳情况下可达到14.49倍.
2. Beijing Key Laboratory of Intelligent Telecommunication Software and Multimedia, Beijing University of Posts and Telecommunications, Beijing 100876, China;
3. School of Computer Science, Beijing University of Posts and Telecommunication, Beijing 100876, China
Aiming at the performance problem of general sparse matrix-matrix multiplication (SpGEMM), a graphics processing unit (GPU)-accelerate SpGEMM algorithm based on task classification and low-latency Hashing table, RBSPARSE, was presented in the paper. RBSPARSE consists of a low-cost pre-analysis method to identify the complexity of sub-tasks, and a Hashing table-based algorithm which could utilize low-latency shared memory to achieve max efficiency. By taking the load balancing issue and the memory latency issue into consideration, RBSPARSE could significantly reduce the overall time in computation. RBSparse and BHSparse are compared. BHSparse is the previous state-of-the-art algorithm for SpGEMM. The result shows that our algorithm is 3.1 times faster than BHSparse on average, and could achieve a maximum 14.49 times faster speed in the best scenario.
一般稀疏矩阵-矩阵乘法(SpGEMM, general sparse matrix-matrix multiplication)是给出稀疏矩阵m×k的A和k×n的B,求m×n的C的过程.在许多领域,例如代数多重网格法[1]、广度优先搜索、最短路径问题和某些图问题(如图聚类block[2]等),SpGEMM都是算法的重要构成部分.因此SpGEMM效率的提升,对于许多领域都有重要意义.
与传统的中央处理器(CPU, central processing unit)相比,图形处理器(GPU, graphic processing unit)可以提供更高的运算性能和内存带宽[3-5].近年来,一些作者利用GPU在浮点运算和内存带宽上的优势对SpGEMM算法进行加速.目前已有的加速算法已取得了良好的效果,但是仍然有限,因为算法中频繁的全局内存(global memory)访问造成的内存延迟和粗放的任务分配所导致的负载极度不均衡[6-7].在SpGEMM中,某些情况下计算所产生的中间产品会达到最终实际结果数量的10倍甚至更多.已有算法中,合并中间产品往往采用排序的方法,在全局内存上进行,使得计算效率低.最近,Liu等[8]采用寄存器和共享内存(shared memory)来进行SpGEMM的加速工作,效果仍不够理想.
提出了低开销的预分析方法,将矩阵的每行按照标准进行分组,以达到良好的负载平衡,并在不同情况下充分利用宝贵的共享内存.对不同的组按行来组织计算,用共享内存上的散列表处理中间产品,以减少内存周期延迟和合并中间产品所带来的大量时间开销.
1 背景知识 1.1 GPU编程GPU诞生的动机是图形处理,并在随后的发展中获得了更为一般的设计目的,即高度并行化的计算密集型场景.笔者以NVIDIA公司生产的GPU为例进行说明.
GPU执行任务分配的基本处理单元是多核处理器(SM, stream multiprocessor),其中包含许多流处理器(SP, stream processor)用于单一线程的执行. SM采用单指令多线程(SIMT, single instruction multiple threads)的方式同时运行大量线程.
为了有效利用GPU的计算资源,同时提供一个基于硬件实现又相对统一的模型,NVIDIA公司提出了统一计算设备架构(CUDA, compute unified device architecture)的概念. CUDA的设计参考底层硬件设计的同时又为应用程序提供了在不同硬件上使用同一模型的便利. RBSparse的代码开发均基于CUDA实现.
1.2 内存延迟内存延迟是指等待内存数据访问完成时引起的延迟.主要因为处理器与内存的频率差异,若某处理器主频近4GHz,而内存频率仅为400MHz,时钟速度之比为10:1,当处理器访问内部高速缓存之外的数据项时,每个周期必须等待10个时钟周期才能使内存芯片完成数据的提取和发送.通常,这些提取需要多个内存周期,然后需要更长时间到达处理器.这就意味着提取数据会占数百个处理器时钟周期,在此期间应用不能处理其他任何任务.
NVIDIA公司的GPU上,可被操作的内存分为全局内存和共享内存.全局内存大小一般在GB数量级,GPU上任何流处理器的任何线程都可访问到它.全局内存一般有300~600个流处理器时钟周期的访问延迟.共享内存只能被同SM的线程访问到,即一个线程块(block)内的线程. CUDA允许的每个线程块的最大共享内存大小为48KB.共享内存的访问延迟一般为20个左右的流处理器时钟周期.
2 相关工作及问题 2.1 BHSparseBHSparse[6]是一种快速的GPU上SpGEMM算法,其提出了一种估计未合并的C矩阵(称为Ct矩阵)的每行非零元素个数上限的方法. Ct矩阵的每行非零元素个数上限进行估计,按照估值对C矩阵各行进行分组申请内存,用不同排序方法对其进行处理.
某些情况下,估值与实际内存需求相差很大,某些行压缩率可达10%,在申请内存时造成了极度浪费,从而性能下降;另一方面,按照此分组方式,某些组的排序方法无效,比如堆排序会造成线程歧义,大于512上限的行被粗略地统一处理,逐步申请内存,造成分歧.
2.2 BalancedHashBalancedHash[9]利用散列表来尽量消除随机的全局内存访问,并提出了一种优化散列表性能的方法来估计输出矩阵中非零值数量,达到了平均1.5倍BHSparse性能的加速效果.
然而,BalancedHash生成工作表占总体时间开销1/4左右.另外,跨行的分块方法并不有效,某些情况下,跨行造成内存访问性能严重下降.
2.3 CUSPCUSP[10]库使用扩展、排序和压缩(ESC, expansion, sorting and compression)的方法.首先,算法生成或展开所有中间产品,并存储在一个数组C*中.然后,使用基数排序按行和列对C*中的条目进行排序.最后,将具有相同行和列索引条目相加以计算矩阵C的非零值.该方法思路清晰,但粗放的中间产品处理办法使负载不均衡,时间成本高. Dalton等[10]在新版本中对其做出了改进,但是不能有效地改进工作效率.
3 优化动机 3.1 SpGEMM主要开销首先介绍SpGEMM算法.假设有2个稀疏矩阵A和B,须计算C=A×B. A和B通常以只记录非零元素(COO, coordinate)或按行压缩(CSR, compressed sparse row)格式存储. mij表示矩阵M第i行第j列位置的元素,mi*表示矩阵M第i行的所有元素,m*j表示矩阵M第j列的所有元素.
首先,将矩阵C中的所有值初始化为空.其次,对于A的每一行,遍历行中的非零元素.如果元素位于第j列,继续遍历矩阵B的第j行.给定bj*中的非零元素,比如在第k列,计算一个中间乘积value=aijbjk.然后,检查cik是否仍然为空,若是,设置cik←value; 否则,设置为cik←cik+value.最后,遍历一行ai*后,生成输出行ci*中的所有值.算法1中展示了该过程.
算法1 SpGEMM的伪代码
1 for each ai* in the matrix A do
2 set ci* to empty
3 for each nonzero entry aij in ai* do
4 load bj*
5 for each nonzero entry bjk in bj* do
6 value ←aijbjk
7 if cik is not belong to ci* then
8 insert cik to ci*
9 cik←value
10 else
11 cik←cik+value
12 end if
13 end for
14 end for
15 end for
算法1中,在SpGEMM的一行的运算中,A中的每个非零元素与B中对应列的非零元素做乘法后,需要进行插入操作,放置在临时的Ct矩阵的对应行的相应位置,若该位置存在元素,则与之合并.总之,SpGEMM算法的主要时间开销集中在算法1的第7~11行,即合并和排序的过程.现有GPU上SpGEMM算法大都在内存延迟更高的全局内存上组织计算.
3.2 按行组织计算在SpGEMM的运算过程中(不考虑运算过程中中间产品的暂存方法),跨行组织运算——每一块任务的分割边界在一行内部,会造成内存访问无法尽可能高效地使用共享内存.
式(1)给出了较小矩阵A和B便于说明原理,axy表示矩阵A x行y列位置的元素.如果在运算时,a23至a31的元素c, 0, d被分配到一个block[1]进行运算,a32至a34的元素0, e, 0被分配到下一个blockblock[2]进行运算.
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{\rm{ }}0}&{{\rm{ }}0}&a&{{\rm{ }}0}\\ {{\rm{ }}0}&b&c&{{\rm{ }}0}\\ d&{{\rm{ }}0}&e&{{\rm{ }}0}\\ {{\rm{ }}0}&{{\rm{ }}0}&{{\rm{ }}0}&f \end{array}} \right], {\rm{ }}\mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {{\rm{ }}0}&{{\rm{ }}h}&a&{{\rm{ }}0}\\ {{\rm{ }}i}&j&c&{{\rm{ }}0}\\ 0&{{\rm{ }}k}&e&{{\rm{ }}l}\\ {{\rm{ }}m}&{{\rm{ }}0}&{{\rm{ }}0}&n \end{array}} \right] $ | (1) |
对于block[1],首先,矩阵A中第2行元素c和矩阵B中第3行非零元素k, l做乘法,分别得到c22=ck, c24=cl.然后,矩阵A中第3行元素d和矩阵B中第1行元素h做乘法,得到c32=dh.此时,block[1]所分配的共享内存被写入c22=ck, c24=cl, c32=dh.
对于blockblock[2],矩阵A中第3行元素e与矩阵B中第3行元素k, l做乘法,分别得到c32=ek, c34=el.可以看到,该块运算存储c32需要与block[1]中的数据求和,造成了2个方面的问题:共享内存并不能跨线程块访问,为了解决该问题,必须在每个线程块运算完成后立即将数据拷贝到全局内存中再进行操作,这将付出高额的时间代价;不同线程块的数据拷贝到共享内存中后,需要进行下一步的合并、排序操作.因此,在RBSparse中按照行来组织运算.
4 主要方法文中所指的稀疏矩阵乘法问题为C=A×B在A=B时的情况.
基本思路是:首先,对矩阵每行的计算情况和整体特性进行分析;其次,按照划分标准将计算量相近的行的行号记录至散列表大小不同的组中;然后,同时发射几个内核,按行组织计算,每个线程块计算一行,充分使用共享内存,发生溢出的行统一进行常规计算;最后,将计算结果进行回测,测试通过后复制回主机内存.
4.1 行计算密度使用单个GPU线程来计算数组nnz_RowCt中的每个元素.算法2描述了该过程.
算法2 计算C矩阵中间产品行上限的伪代码
1 for each entry nnz_RowCti in nnz_RowCt in parallel do
2 nnz_RowCt[i]← 0
3 for each nonzero entry aij in ai* do
4 nnz_RowCt[i]←nnz_RowCt[i]+nnz(bj*)
5 end for
6 end for
创建一个大小为m的数组nnz_RowCt,其中m=n是矩阵C的行数,nnz_RowCt[i]存储了矩阵C第i行的中间产品数量上限,称之为行计算密度,nnz(bj*)为矩阵B第j行的非零元素个数(下同).
4.2 散列表如图 1所示,算法定义每个散列表最多可以存储多少个中间变量为散列表的大小.在数组idx中写入结果的列标,在数组val中写入结果的值.

|
图 1 散列表在共享内存上的示意图 |
每个idx[i]为一个整型,占4Byte,每val[i]为一个双精度浮点型,占8Byte,即每个位置需要12Byte.当散列表大小为128时,占用1.5KB的共享内存.在实验中使用的NVIDIA GTX 1070上,每个线程块上支持的最大共享内存大小为48KB.当散列表大小为4096时,占用共享内存为48KB,是最大情况.
4.3 计算的均衡特征根据矩阵C中间产品每行非零元素个数上限的方差来确定该矩阵计算的均衡特性.定义当方差除以Ct每行非零元素平均值小于等于0.5时(即
对于均衡计算型矩阵,因为矩阵C中间产品每行非零元素个数上限(下文称为行计算密度)的方差不大,即在整体计算过程中每行的计算量波动并不大,所以在计算过程中可以使用一个统一的散列表大小进行计算,而不会造成共享内存的浪费.
详细地讲,对于非均衡计算型行矩阵,计算过程中每行计算量的波动相对较大,例如极端情况下,某Ct矩阵的上限个数在少的行为32,在多的行为4096,而且这些行还都在矩阵计算中占据了不可忽视的比例.
如果统一设定散列表大小为4096,对于分到行计算密度为1的行的线程块,分配的num_threads个线程在单位时间内最多只有一个在运行状态,这样就会造成极大的资源浪费.
如果统一设定散列表大小为32,对于分到行计算密度为4096的行任务的线程块,散列表就会出现严重的冲突和溢出,这样也会使得整体性能发生显著下降.因此,对于非均衡计算型矩阵应根据行计算密度的大小进行分区,将行计算密度接近的行划分为一组,以一个统一的散列表大小进行运算,以达到尽可能好的资源利用,提升计算性能.
4.4 散列表大小的分组将散列表按大小分为6组,即Group[0]~Group[5],大小分别为32、64、128、256、512和2048,用
但是,实际大多数情况下,中间产品都将发生合并,所以使用nnz_RowCt除以π,这样每个块内散列表既不会发生严重的冲突,又可以尽可能多地节省计算资源,使一个SM尽可能多地同时进行计算.
1) 预处理
读取COO格式的矩阵A,并以CSR格式写入GPU全局内存中,以便使用.
2) 预分析
① 计算行计算密度
进行计算密度nnz_RowCt数组的计算,以供使用和参考.
② 计算方差
计算nnz_RowCt的方差,用于区分均衡计算型和不均衡计算型2种矩阵,并以不同的处理方法进行计算.
3) 分组
① 均衡计算型\非均衡计算型矩阵
根据
② 非均衡计算型矩阵不同的散列表大小
根据
当0≤α < 32时,该行被分配至Group[0];
当32≤α < 64时,该行被分配至Group[1];
当64≤α < 128时,该行被分配至Group[2];
当128≤α < 256时,该行被分配至Group[3];
当256≤α < 512时,该行被分配至Group[4];
当512≤α时,该行被分配至Group[5].
4) 计算
以散列表大小为128为例. RBSparse在主机上发射内核(在GPU上执行的代码),并将指定的参数(线程块数目和每块线程数目)和数组信息一并传递.
① 计算与合并
利用共享内存上的散列表来实现计算与合并的过程,最初散列表的idx数组被全部初始化为⊥,val数组被全部初始化为0.
首先,将矩阵A的一行的非零元素分给每个线程,每个线程处理一个非零元素.每个线程遍历与该元素aij需要做乘法的bjk, 做乘积之后得到value,对下标k做散列,得到h_idx=hash(k),散列函数采用简单的取模运算,将得到的value写入已申请好的散列表的h_idx位置.如此处没有结果,则直接写入k至idx[k],value至val[k];如果此处已有结果,若k和idx[h_idx]相等,则将value累加至val[k],若k和idx[h_idx]不相等,则对散列表中的下一位置进行同样的判断,直到寻找到可以直接写入或合并的位置.如果遍历完整个散列表还未找到可存储的位置,则将当前行标记为无效行,稍后以传统方法统一处理无效行.算法3中的伪代码展示了该过程.
算法3 每个线程向散列表插入中间值的伪代码
1 value ←aijbjk
2 h_idx ← hash(k)
3 for step in 1 to hash_size do
4 h←(h_idx+step) mod hash_size
5 if atomicCAS(idx[h], ⊥, k) = k then
6 atomicAdd(val[h], value)
7 break
8 end if
9 end for
10 if step = hash_size then
11 mark row i as invalid
12 end if
② 排序
对于已经在共享内存中完成计算和合并过程的行,对其按照列标升序进行排序.这里笔者对基础的双调排序(bitonic sort)[11]算法进行改进,以使其在RBSparse中得以高效运行,满足算法的排序需求.在此,不再做详细叙述.
排序完成后,算法将结果拷贝至全局内存中,清空共享内存,继续其他行的运算.
5) 归集
RBSparse对每行使用一个线程,将GPU全局内存中的不同行的数据拷贝到主机(host)内存的连续空间中.
6) 测试
使用CUSP库进行相同矩阵的乘法运算,并将RBSparse的计算结果与其进行比对,比对成功则完成测试.
5 实验方法 5.1 实验平台实验过程中所用详细配置如表 1所示.
|
|
表 1 用于实验的计算机配置详情 |
实验中使用的矩阵如表 2所示,都来自于佛罗里达大学矩阵集合[12],涵盖了理论化学、量子化学、计算流体动力学、2D/3D问题等各个领域.
|
|
表 2 用于实验的矩阵 |
对比了RBSparse算法和现有最快的BHSparse算法的性能,如图 2和图 3所示,以BHSparse的性能为1,RBSparse的速度为其倍数来展示.
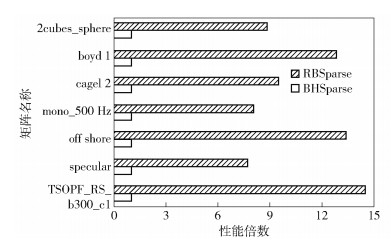
|
图 2 RBSparse与BHSparse性能对比(实验1) |
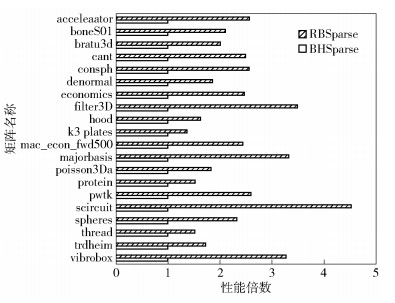
|
图 3 RBSparse与BHSparse性能对比(实验2) |
提出的RBSparse在实验1和2中达到了平均3.1倍的性能表现.在TSOPF_RS_b300_c1矩阵上的表现达到了最佳的14.49倍的性能表现.
6.2 RBSparse与BalancedHash性能对比由于Pham等[9]并没有公开BalancedHash的代码,所以无法直接比较.但是在与其相同的测试矩阵上,RBSparse达到了平均3.32倍BHSparse的性能,优于BalancedHash的平均1.5倍性能.
7 结束语提出了利用散列表和高速的共享内存并按行组织计算来提高GPU上的SpGEMM的性能. RBSparse算法比目前最快的GPU SpGEMM算法BHSparse执行速度平均快3.1倍.在以后的研究中,将进一步研究稀疏矩阵的结构和SpGEMM的复杂性之间的关系,以提高算法的性能,并使其性能在不同的矩阵上得到较为均衡的提升,以及将RBSparse集成到一个通用的GPU稀疏矩阵库中,研究其在实际应用中的使用.
| [1] |
Bell N, Dalton S, Olson L N. Exposing fine-grained parallelism in algebraic multigrid methods[J]. SIAM Journal on Scientific Computing, 2012, 34(4): 123-152. DOI:10.1137/110838844 |
| [2] |
Buluç A, Gilbert J R. The combinatorial BLAS:design, implementation, and applications[J]. International Journal of High Performance Computing Applications, 2011, 25(4): 496-509. DOI:10.1177/1094342011403516 |
| [3] |
Yuan Tao, Huang Zhibin. Shuffle reduction based sparse matrix-vector multiplication on Kepler GPU[J]. International Journal of Grid and Distributed Computing, 2016, 9(10): 99-106. DOI:10.14257/ijgdc.2016.9.10.09 |
| [4] |
Greathouse J L, Daga M.Efficient sparse matrix-vector multiplication on GPUs using the CSR storage format[C]//Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis.New York: IEEE Press, 2014: 769-780.
|
| [5] |
菅立恒, 易卫东. 使用GPU加速无线传感器网络信道仿真[J]. 北京邮电大学学报, 2013, 36(2): 24-27. Jian Liheng, Yi Weidong. Acceleration of simulation of radio channel in wireless sensor networks using GPU[J]. Journal of Beijing University of Posts and Telecommunications, 2013, 36(2): 24-27. |
| [6] |
Liu Weifeng, Vinter B.An efficient GPU general sparse matrix-matrix multiplication for irregular data[C]//2014 IEEE 28th International Parallel and Distributed Processing Symposium.New York: IEEE Press, 2014: 370-381.
|
| [7] |
黄智濒, 周锋, 马华东. 自适应访问模式的缓存替换策略[J]. 北京邮电大学学报, 2016, 39(3): 44-48. Huang Zhibin, Zhou Feng, Ma Huadong. A cache replacement policy adapting to the request access pattern[J]. Journal of Beijing University of Posts and Telecommunications, 2016, 39(3): 44-48. |
| [8] |
Liu Junhong, He Xin, Liu Weifeng, et al.Register-based implementation of the sparse general matrix-matrix multiplication on GPUs[J]. ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming.New York: ACM, 2018: 407-408.
|
| [9] |
Anh P N Q, Fan Rui, Wen Yonggang.Balanced Hashing and efficient GPU sparse general matrix-matrix multiplication[C]//Proceedings of the 2016 International Conference on Supercomputing.New York: ACM, 2016: 36.
|
| [10] |
Dalton S, Bell N, Olson L, et al.CUSP: generic parallel algorithms for sparse matrix and graph computations: Version 0.5[EB/OL]. (2015-03-13)[2018-05-30]. https://cusplibrary.github.io.
|
| [11] |
Batcher K E.Sorting networks and their applications[C]//Spring Joint Computer Conference.New York: ACM, 1968: 307-314.
|
| [12] |
Davis T A, Hu Yifan. The University of Florida sparse matrix collection[J]. ACM Transactions on Mathematical Software, 2011, 38(1): 1. |



























