2. 昆明学院 教师教育学院, 昆明 650214
为提高免测距无线传感器网络节点定位算法的性能,针对免测距定位算法利用最小跳路径距离替代节点间欧氏距离,和信标节点近似共线引入较大定位误差的缺陷,提出基于相交度比的无线传感器网络迭代定位算法,首先利用定位单元拓扑分布质量函数选择1-跳邻居参考节点,组成高质量的定位单元;其次采用基于相交度比的距离计算估计距离精度;最后采用双曲线定位方法减少误差.仿真结果表明,在节点均匀随机部署,非均匀C-型分布的网络场景中,与DV-Hop、Amorphous等已有改进算法相比,新算法具有更小的定位误差,可提供更加精确的传感器节点位置.
2. School of Teacher Education, Kunming University, Kunming 650214, China
In order to improve the performance of range-free localization algorithm such as DV-Hop and Amorphous for wireless sensor network, the problem of using the minimum hop path distance to replace the Euclidean distance between nodes and choosing the approximate collinearity beacons to calculate location of unknown node that introduces large positioning error is studied. An iteration localization algorithm in wireless sensor network based on intersection degree ratio (ILA-IDR) is proposed. The ILA-IDR algorithm first uses the localization group topology distribution quality function to select three 1-hop neighbor reference nodes form a non-collinear positioning unit, and then the distance calculation based on the intersection degree ratio is used to improve the estimation distance accuracy. Finally, the hyperbolic calculation method is adopted to reduce the error to improve the node location accuracy. Simulation shows that the ILA-IDR algorithm is superior to those of the DV-Hop, Amorphous and the advanced algorithm for that the localization error of the ILA-IDR algorithm is lower than those algorithms both in the node uniform and C-Shape distribution scenario.
作为物联网前端技术,无线传感器网络实现了快速部署、组网便捷、低成本的数据收集,具有广阔的应用前景.但是在大多数应用和传感器网络自身拓扑控制、路由等核心技术设计中,传感器节点必须明确自身位置信息[1].无线传感器网络节点受到成本、能耗限制,不可能给所有节点装配定位模块.因此,传感器网络节点必须根据部署在网络中的部分位置已知节点(信标节点)和节点之间的通信关系确定自身的位置,即传感器网络节点定位.现有的定位技术根据定位算法是否直接通过物理测量来获得节点间的距离或角度信息分为测距(range-based)定位技术和免测距(range-free)定位技术[2].测距定位利用物理层无线信号的接收信号强度[3](RSS,received signal strength)、到达时间[4](TOA,time of arrival)、到达时间差[5] (TDOA,time difference on arrival)、到达角度[6] (AOA,angle of arrival),并依据定位几何关系获得定位测量,进而解算位置(坐标)信息.测距定位能获得较高的定位精度,但需要额外的硬件模块来实现测距,实现成本高,工作功耗高;与测距定位不同,免测距定位[7]不直接进行距离(或方位)测量,而是通过估计节点间的欧氏距离或确定包含未知节点的可能区域,进而确定未知节点的位置.经典的免测距定位算法有DV-Hop(distance vector-hop)算法[8]、质心算法(centroid algorithm)[9]、凸规划(convex optimization)算法[10]和MDS-MAP算法[11]等.与测距定位相比,免测距定位免硬件支持,具有成本低、功耗小的特点,更能适应资源受限无线传感器网络的应用需求.
围绕提高免测距定位算法定位精度,石等[12]利用信标节点间平均跳距误差来修正网络平均跳距,使未知节点估算到信标节点的距离更加精确,Lee等[13]采用最小化平均跳距误差修正提高定位精度. iDV-Hop和iDV-Hop2算法[14]估算距离加权修正和二次规划及线性规划计算方法来减少定位误差,在条件限制下2种计算方法归结为优化问题,增加了算法的计算复杂性. HDV-Hop[15]采用跳数修正和信标节点部署到边缘位置实现传感器节点定位,目标实现定位过程的能量最小化.先进DV-Hop定位算法[16]通过跳数加权,降低了通信跳数大的信标节点对节点定位的影响,减少了引入的定位误差.未知节点完成定位后,再进行误差修正,进一步提高了定位精度.基于分簇的定位[17]将网络分簇,然后在簇内实现分布式定位,关注点是减少定位过程中网络通信负载.基于3个信标节点选择的DV-Hop[18]利用3个信标节点完成定位计算,但3个信标节点的选择使用了临近节点,其跳数向量相似判定原则,其准确性较差.最新的研究引入RSS距离测量的RHOP-ELM-RCC[19]算法、基于极限机器学习的神经网络算法,以提高DV-Hop的距离准确性和定位精度.基于智能算法[20]、神经网络[21]、移动信标节点协助[22-23]和定位参考节点选择[24]策略可分成4类,基于跳距修正方法定位性能提升有限,同样不适用于节点非均匀分布的无线传感器网络的应用.基于分簇和信标节点选择方法的关注目标在于减少计算复杂性和通信负载.引入粒子群、神经网络的智能方法必将增加算法计算复杂性.移动信标节点需要执行移动信标节点路径规划算法.
在研究DV-Hop免测距算法的基础上,提出了基于相交度比的无线传感器网络迭代定位算法(ILA-IDR,iteration localization algorithm in wireless sensor network based on intersection degree ratio),通过信标节点选择、新的距离计算和边界节点补偿提高定位性能,最后给出仿真结果和分析.
1 DV-Hop算法及误差分析DV-Hop、Amorphous等免测距定位算法首先利用信标节点间的通信跳数和欧氏距离计算网络平均每跳距离,然后未知节点利用到信标节点的跳数与网络平均跳距计算自己到信标节点的距离,最后使用最小二乘法计算位置坐标完成定位.
首先,传感器网络节点通过信息交换,所有节点获取到其他节点的最小通信跳数以及信标节点位置.其次,每个信标节点利用式(1)计算以自己出发的平均每跳距离.
| $ {L_i} = \frac{{\sum\limits_{i \ne j} {\sqrt {{{\left( {{x_i} - {x_j}} \right)}^2} + {{\left( {{y_i} - {y_j}} \right)}^2}} } }}{{\sum\limits_{i \ne j} {{H_{ij}}} }} $ | (1) |
其中:(xi, yi)和(xj, yj)分别为信标节点i和信标节点j的位置坐标,Hij为信标节点i到信标节点j的最小通信跳数.信标节点计算出平均每跳距离后,将其广播给网络中所有节点.未知节点收到信标节点的Li后,利用式(2)估算到信标节点的距离.
| $ {d_{ui}} = {L_i} \times {H_{ui}} $ | (2) |
其中Hui是未知节点u距离信标节点i的最小跳数.最后,未知节点u获取到n个信标节点的距离后,设节点u位置坐标为(x, y),信标节点i的位置坐标(xi, yi),u到i估计距离为di,则使用式(3)完成未知节点u的定位计算.
| $ \left. {\begin{array}{*{20}{c}} {{{\left( {x - {x_1}} \right)}^2} + {{\left( {y - {y_1}} \right)}^2} = d_1^2}\\ {{{\left( {x - {x_2}} \right)}^2} + {{\left( {y - {y_2}} \right)}^2} = d_2^2}\\ \vdots \\ {{{\left( {x - {x_n}} \right)}^2} + {{\left( {y - {y_n}} \right)}^2} = d_n^2} \end{array}} \right\} $ | (3) |
变换成矩阵形式AX=B,其中,
| $ \mathit{\boldsymbol{A}}{\rm{ = }}\left( {\begin{array}{*{20}{c}} {{x_1} - {x_n}}&{{y_1} - {y_n}}\\ {{x_1} - {x_n}}&{{y_1} - {y_n}}\\ \vdots & \vdots \\ {{x_{n - 1}} - {x_n}}&{{y_{n - 1}} - {y_n}} \end{array}} \right) $ |
| $ \mathit{\boldsymbol{B}} = \left( {\begin{array}{*{20}{c}} {d_1^2 - d_n^2 + x_1^2 - x_n^2 + y_1^2 - y_n^1}\\ {d_2^2 - d_n^2 + x_2^2 - x_n^2 + y_1^2 - y_n^1}\\ \vdots \\ {d_{n - 1}^2 - d_n^2 + x_{n - 1}^2 - x_n^2 + y_{n - 1}^2 - y_n^1} \end{array}} \right) $ |
用最小二乘法完成未知节点位置计算,未知节点u的坐标为
| $ \mathit{\boldsymbol{X}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{B}} $ | (4) |
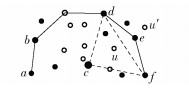
分析DV-Hop算法的定位过程,存在3个误差来源.一是距离模糊问题,使用信标节点计算出的平均跳距并不能准确替代全网平均跳距,尤其在节点分布不均匀的网络场景中,且距离信标节点通信跳数相同的节点,按式(2)计算的距离相等;二是存在奇异路径问题,DV-Hop算法用最小跳数路径距离替代节点间的欧氏距离,在节点分布不均匀时,最小跳数路径严重偏离欧氏距离路径,称之为奇异路径,引入的距离估计误差较大;三是在多边定位计算中,信标节点共线或者逼近共线导致计算矩阵奇异,不满足可定位的冗余刚性条件[19],定位误差增大甚至不可定位.如图 1所示,未知节点u定位时,信标节点d、e、f逼近共线,也不利于定位计算,图中u和u′临近区域均可能成为其定位位置,其最好定位参考节点应选择c、d、f.
|
图 1 共线性定位单元 |
基于相交度比迭代定位算法采用迭代定位方式,每轮分为邻居节点发现、定位单元选择、距离估计、定位计算4个阶段.
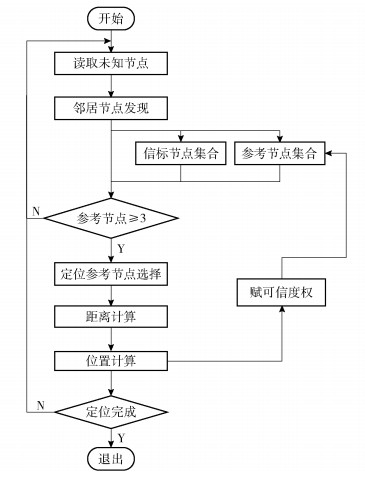
2.1 算法描述首先选择1-跳邻居中参考节点个数大于3的未知节点,将其1-跳参考节点作为候选节点,利用定位单元信任度函数计算出拓扑分布质量最高的参考节点组成定位单元,去除共线或逼近共线的参考节点.然后基于节点间的相交度来估计未知节点到选定定位单元参考节点间的距离,去除距离模糊问题.最后使用双曲线计算方法完成位置计算,将其升级成下一轮定位时的参考节点,基于相交度比迭代定位算法流程如图 2所示.
|
图 2 基于相交度比迭代定位算法流程 |
信标节点:网络部署时,配置了精确位置的节点,选择参考节点时,赋予较高的可信度.
参考节点:通过上轮定位计算,实现定位的节点,将其升级为本轮定位的参考节点,赋予较低的可信度.
邻居节点集Ni:Ni={j|dij≤r且j≠i},其中,dij为节点i和节点j之间的距离,r为节点通信半径.
定位单元:节点u定位时,只需要3个位置已知节点,将这3个位置已知节点称为未知节点u的定位单元组,记作:
相交度比:定义为落在两相邻节点相交区域的传感器节点数的2倍与2个相邻节点的邻居节点数和之比.即
| $ {\mathit{I}_{ij}} = \frac{{2\left| {{N_i} \cap {N_j}} \right|}}{{\left| {{N_i}} \right| + \left| {{N_j}} \right| + 2}} $ | (5) |
信标节点i生成元数据,包含自身序号、位置坐标和跳数等字段,即(id, (xi, yi), hops)的3元组.其中,hops字段的初始值为0,向周围邻居节点广播出去,邻居节点接收该元数据后,将跳数字段hops值置1,并将该节点记录到自己的邻居参考节点表V中.
未知节点j生成元数据,包括自身序号、位置坐标和跳数字段,即(id, (xj, yj), hops)的3元组,将(xj, yj)和hops字段初值均设置为0,向周围邻居节点广播.邻居节点接收该元数据后,将hops字段值加1,并将该节点记录到自己的邻居节点表V中.
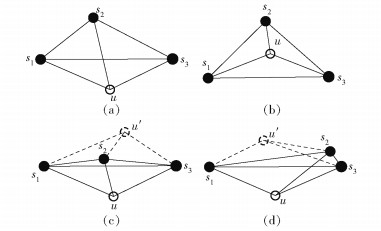
2.4 定位单元选择对未知节点u定位时,DV-Hop算法使用全部信标节点,其中,共线节点跳数大和估计距离误差大的节点参与计算,导致定位不精确.分析定位单元的拓扑结构对节点u的定位精度影响,拓扑分布如图 3所示.图 3(a)和(b)中,3个参考节点几何分布较好,接近正三角形,距离估计误差影响较小,对u的定位精度影响较小,而在(c)和(d)中,3个参考节点几何分布较差,距离估计误差易将3个参考节点估计成共线或逼近共线,致使lg (u)不满足冗余刚性[25]条件,导致u的定位精度差,甚至不可定位.因此,建立定位单元组的信任度计算函数为
| $ c = \frac{{2{h_{\min }}}}{{\sqrt 3 {l_{\max }}}} $ | (6) |
|
图 3 定位单元组拓扑分布 |
其中:lmax为定位三角形最长边长,hmin为三角形依附于最长边长的高.设未知节点j定位时,其邻居参考节点表V中有m个候选节点,构成Cm3个定位单元组,按式(6)计算出其c,选择c最大3个信标节点作为未知节点u的定位单元组lg (u).
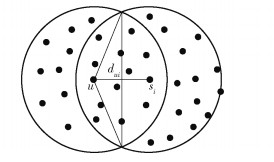
2.5 距离估计 2.5.1 节点距离估计选定的定位单元lg (u)的节点si均是节点u的1-跳邻居节点,分布如图 4所示.
|
图 4 邻居节点分布 |
交叉区域面积susi为
| $ {s_{u{s_i}}} = 2{r^2}\arccos \left( {\frac{{{d_{u{s_i}}}}}{{2r}}} \right) - {d_{u{s_i}}}\sqrt {{r^2} - \frac{{d_{u{s_i}}^2}}{4}} $ | (7) |
令
| $ \frac{{{s_{u{s_i}}}}}{{{r^2}}} = 2\arccos \left( x \right) - 2x\sqrt {1 - {x^2}} $ | (8) |
泰勒级数展开有
| $ \arccos \left( x \right) = \frac{{\rm{ \mathsf{ π} }}}{2} - x - \frac{1}{6}{x^3} - \frac{3}{{40}}{x^5} - \cdots $ |
| $ x\sqrt {1 - {x^2}} = x - \frac{{{x^3}}}{2} - \frac{{{x^5}}}{8} - \cdots $ |
代入式(8),有
| $ \frac{{{s_{u{s_i}}}}}{{{r^2}}} = {\rm{ \mathsf{ π} }} - 4x + \frac{2}{3}{x^3} + \frac{1}{{10}}{x^5} - \cdots $ | (9) |
由于x取值在[0, 1],忽略掉3次方后的项,则
| $ \frac{{{s_{u{s_i}}}}}{{{r^2}}} = {\rm{ \mathsf{ π} }} - 4x $ | (10) |
即
| $ \frac{{{s_{u{s_i}}}}}{{{\rm{ \mathsf{ π} }}{r^2}}} = 1 - \frac{{2{d_{u{s_i}}}}}{{{\rm{ \mathsf{ π} }}r}} $ | (11) |
设传感器网络随机均匀分布于任务区域,λ为节点密度,面积为D的区域,分布的传感器节点数是泊松分布模型,其概率密度函数为
| $ p\left( {K = k} \right) = \frac{{{{\left( {\lambda D} \right)}^k}}}{{k!}}{{\rm{e}}^{\lambda D}} $ | (12) |
定理1 在传感器网络节点均匀分布时,节点服从式(12)的泊松分布,对于定位单元lg (u)中,式(13)成立.
| $ \frac{{{s_{u{s_i}}}}}{{{\rm{ \mathit{ π} }}{r^2}}} = {I_{u{s_i}}} $ | (13) |
定理1推导过程可参照文献[26],则未知节点u和si的距离为
| $ {d_{u{s_i}}} = \frac{1}{2}\left( {1 - {I_{u{s_i}}}} \right){\rm{ \mathit{ π} }}r $ | (14) |
式(14)为未知节点u和定位单元lg (u)的信标节点si距离计算.对于部署区域中间的节点,距离估计较为精确.而边界节点,这种距离估计误差较大,因此,边界节点需要加权处理,Yue等[27]给出了一种优秀的边界节点识别方法,但计算处理较为复杂.利用节点连通度信息进行判定,节点对〈su, si〉分2种情况处理.
1) 节点随机均匀分布
信标节点si依据其位置信息来判定是否为边界节点.对于节点u,如果其邻居节点数满足mu≤
对于边界节点,如果2个同时为边界节点,不做补偿处理.如果只有一个边界节点时,用式(15)来补偿边界节点的邻居节点数.
| $ \begin{array}{*{20}{c}} {m = {C_{{\rm{degree}}}}}\\ {{m_{{\rm{insec}}}} = \frac{5}{4}{m_{{\rm{insec}}}}} \end{array} $ | (15) |
2) 节点非均匀分布
在非均匀分布的网络中,如果其邻居节点数满足
未知节点定位计算时,当信标节点比例设置较小时,节点1-跳通信范围内信标节点个数小于3个时,节点不能完成定位.因此,采用迭代定位方式,将上轮完成定位计算的节点升级为参考节点,赋予一个较低的信任度,参与本轮节点的定位.
设未知节点u的位置为(xu, yu),定位单元组lg(u)中参考节点si位置(xi, yi).位置计算过程为
| $ {\left( {{x_i} - {x_u}} \right)^2} + {\left( {{y_i} - {y_u}} \right)^2} = d_{iu}^2 $ | (16) |
即有
| $ \left. {\begin{array}{*{20}{c}} { - 2{x_1}{x_u} - 2{y_1}{y_u} + x_u^2 + y_u^2 = d_{u1}^2 - x_1^2 - y_1^2}\\ { - 2{x_2}{x_u} - 2{y_2}{y_u} + x_u^2 + y_u^2 = d_{u2}^2 - x_2^2 - y_2^2}\\ { - 2{x_3}{x_u} - 2{y_3}{y_u} + x_u^2 + y_u^2 = d_{u3}^2 - x_3^2 - y_3^2} \end{array}} \right\} $ | (17) |
令
| $ {A_i} = x_i^2 + y_i^2,B = x_u^2 + y_u^2 $ |
| $ \mathit{\boldsymbol{Z}}{\rm{ = }}{\left[ {{x_u},{y_u},B} \right]^{\rm{T}}} $ |
| $ \mathit{\boldsymbol{G}} = \left( {\begin{array}{*{20}{c}} { - 2{x_1}}&{ - 2{y_1}}&1\\ { - 2{x_2}}&{ - 2{y_2}}&1\\ { - 2{x_3}}&{ - 2{y_3}}&1 \end{array}} \right) $ |
| $ \mathit{\boldsymbol{H}}{\rm{ = }}\left( {\begin{array}{*{20}{c}} {d_{u1}^2 - {\mathit{\boldsymbol{A}}_1}}\\ {d_{u2}^2 - {\mathit{\boldsymbol{A}}_2}}\\ {d_{u3}^2 - {\mathit{\boldsymbol{A}}_3}} \end{array}} \right) $ |
则式(17)表示为
| $ \mathit{\boldsymbol{GZ}}{\rm{ = }}\mathit{\boldsymbol{H}} $ | (18) |
则Z的计算公式为
| $ \mathit{\boldsymbol{Z}}{\rm{ = }}{\left( {{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{G}}} \right)^{ - 1}}\mathit{\boldsymbol{GH}} $ | (19) |
所以未知节点u的坐标为
| $ \left( {{x_u},{y_u}} \right) = \left( {\mathit{\boldsymbol{Z}}\left( 1 \right),\mathit{\boldsymbol{Z}}\left( 2 \right)} \right) $ | (20) |
Matlab R2012a中,在1000m×1000m的任务区域投放300个传感器节点,传感器节点在任务区域呈随机均匀分布和非均匀C型分布的2种应用场景中进行仿真实验.在C型分布场景中,左上角传感器节点分布较为密集,右下角较为稀疏,右中部分没有节点部署.定位时,信标节点可信度设置为1,参考节点的可信度设置为迭代轮数的倒数.定位单元选择时,优先选择信标节点,当信标节点数不到3个时,参考节点参与运算.从不同信标点比例和不同的通信半径设置上,对传统的DV-Hop算法、Amorphous、文献[12]算法,先进DV-Hop定位算法和提出的ILA-IDR算法性能进行仿真实验验证分析.实验从整体网络的平均定位误差比较考查算法的定位性能.平均定位误差(ALE, average localization error)按式(21)定义.
| $ E = \sum\limits_{i = 1}^{N - M} {\frac{{\sqrt {{{\left( {{{\hat x}_i} - {x_i}} \right)}^2} + {{\left( {{{\hat y}_i} - {y_i}} \right)}^2}} }}{{r\left( {N - M} \right)}}} $ | (21) |
其中:
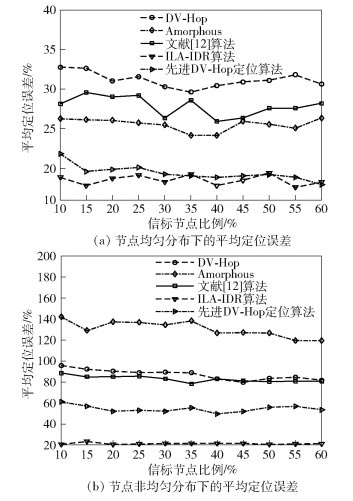
信标节点比例设置为10%~60%,步长增长值为5%,仿真10次,平均定位误差取平均值,图 5所示为DV-Hop定位算法、Amorphous,文献[12]算法,先进DV-Hop定位算法和ILA-IDR算法的平均定位误差.
|
图 5 不同信标节点比例下的平均定位误差 |
在均匀的C型分布中,DV-Hop算法定位误差最大,平均大于30%,文献[12]算法次之,定位误差震荡在26%~30%,之后为Amorphous算法,定位误差值在25%~26%之间,再次是先进DV-Hop定位算法,而ILA-IDR算法的定位误差最小,维持在18%~20%之间,定位精度最高.在非均匀的C型分布中,随着信标节点比例的提高,DV-Hop算法、Amorphous算法和文献[12]算法,定位误差整体呈下降趋势. Amorphous算法定位误差最大,大于120%,DV-Hop次之,其次为文献[12]算法,两者的定位误差均大于80%,再次为先进DV-Hop定位算法,误差在60%左右,而提出的ILA-IDR算法维持在21%左右,相比于前4种算法,定位误差非常小,定位精度很高.
综合图 5来看,DV-Hop算法、Amorphous算法、文献[12]算法和先进DV-Hop定位算法在节点均匀分布时,定位误差较小,而在非均匀分布中,定位误差很大.而ILA-IDR算法采用了定位单元信任函数来选择1-跳邻居中拓扑分布最好的参考节点,均是未知节点邻居,且消除了信标节点共线问题引入的定位误差.同时采用基于相交度的距离估计,减小了距离估计误差.所以在2种拓扑结构下,定位误差几乎不受节点分布影响,相差2%左右,而且只需要选择3个定位参考节点,所以预设信标节点比例影响很小.
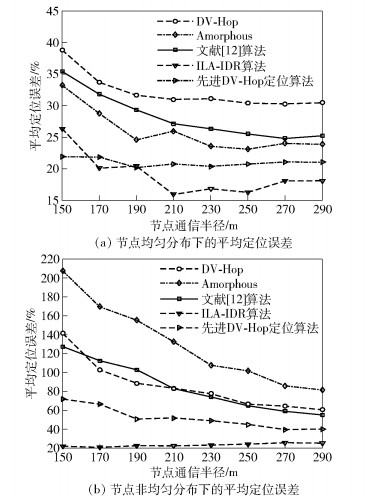
3.2 节点通信半径对定位性能的影响设置节点的通信半径为150~290m,步长增长值为20m.图 6所示为5种算法的定位误差结果.
|
图 6 不同通信半径时的平均相对定位误差 |
在节点均匀分布应用中,随着通信半径增大,5种算法定位误差整体呈下降趋势. DV-Hop算法定位误差最大,大于30%,文献[12]算法次之,其次是Amorphous算法,2个算法定位误差大于25%,先进DV-Hop定位算法次小,而ILA-IDR算法最小,信标节点通信半径170m后就下降到20以下.
在节点非均匀分布的C型结构中,随着信标节点比例的提高,DV-Hop算法、Amorphous算法、文献[12]算法和先进DV-Hop定位算法定位误差整体呈下降趋势,而ILA-IDR算法保持不变.另外,Amorphous算法定位误差最大,DV-Hop和文献[12]算法,两者的定位误差相当,均大于60%,先进DV-Hop定位算法次小,但大于40%,而ILA-IDR算法维持在21%左右,相比于前4种算法,定位误差非常小,定位精度很高.
综合图 6来看,DV-Hop算法、Amorphous算法、文献[12]算法和先进DV-Hop定位算法,在节点均匀分布时,定位误差较小,而在非均匀分布中,定位误差很大.同理,ILA-IDR算法采用了定位单元信任函数来选择1-跳邻居中拓扑分布最好的参考节点,均是未知节点邻居,且消除了信标节点共线问题引入的定位误差,所以定位精度几乎不受节点分布影响.同时采用基于相交度的距离估计,使得传感器节点通信半径变化对距离的估计影响很小,估计的误差也较小,所以实验中ILA-IDR算法的定位误差受传感器节点分布和节点通信半径变化的影响都很小.
4 结束语传统的DV-Hop算法、Amorphous算法及改进算法采用信标节点间的平均跳距来替代全网节点的平均跳距,进而估计节点间的距离,存在估计误差,在节点非均匀分布时,误差更大.同时全网信标节点参与定位,共线节点也容易引入误差.采用3个信标节点接近正三角形分布时,引入定位误差最小原理及利用邻居节点相交度比来估计节点间距离和双曲线定位法等手段完成节点定位,从而提高节点定位精确性.仿真实验结果说明,ILA-IDR算法定位精度较高,是一种受网络节点拓扑分布影响很小的高效定位.
| [1] |
王福豹, 史龙, 任丰原. 无线传感器网络中的自身定位系统和算法[J]. 软件学报, 2005, 16(5): 857-868. Wang Fubao, Shi Long, Ren Fengyuan. Self-localization systems and algorithms for wireless sensor networks[J]. Journal of Software, 2005, 16(5): 857-868. |
| [2] |
Asma M, Mohammed F, Nabila L. Wireless sensor networks localization algorithms:a comprehensive survey[J]. International Journal of Computer Networks & Communications, 2013, 5(6): 45-64. |
| [3] |
Niculeseu D, Nath B.Ad-hoc positioning systems(APS)[C]//Proceedings of the 2001 IEEE Global Telecommunications Conference.San Antonio: IEEE, 2001: 2926-2931.
|
| [4] |
Patwari N, Hero A O, Perkins M, et al. Relative location estimation in wireless sensor networks[J]. IEEE Transactions on Signal Processing, 2003, 51(8): 2137-2148. DOI:10.1109/TSP.2003.814469 |
| [5] |
Girod L, Estrin D.Robust range estimation using acoustic and multimodal sensing[C]//Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems.Maui: IEEE, 2001: 1312-1320.
|
| [6] |
Lazos L, Poovendran R, Capkun S.POPE: robust position estimation in wireless sensor networks[C]//Proceedings of the 4th IEEE International Symposium on Information Processing in Sensor Networks.Boise: IEEE, 2005: 324-331.
|
| [7] |
肖竹, 王东, 李仁发, 等. 物联网定位与位置感知研究[J]. 中国科学:信息科学, 2013, 43(10): 1265-1287. Xiao Zhu, Wang Dong, Li Renfa, et al. Localization and nodes location-aware in internet of things[J]. Science China:Information, 2013, 43(10): 1265-1287. |
| [8] |
Niculescu D, Nath B. DV-based positioning in Ad hoc networks[J]. Telecommunication System, 2003, 22(1-4): 267-280. |
| [9] |
Bulusu N, Heidemann J, Estrin D. GPS-less low-cost outdoor localization for very small devices[J]. IEEE Personal Communications, 2000, 7(5): 28-34. DOI:10.1109/98.878533 |
| [10] |
Doherty L, Pister K S J, El Ghaoui L.Convex position estimation in wireless sensor networks[C]//Proceeding of Joint Conference of the IEEE Computer and Communications Society.Anchorage: [s.n.], 2001: 1655-1663.
|
| [11] |
Shang Y, Ruml W, Zhang Y, et al.Localization from mere connectivity[C]//Proceeding of the 4th ACM International Symposium on Mobile Ad hoc Networking and Computing.New York: ACM, 2003: 201-212.
|
| [12] |
石为人, 贾传江, 梁焕焕. 一种改进的无线传感器网络DV-Hop定位算法[J]. 传感技术学报, 2011, 24(1): 83-87. Shi Weiren, Jia Chuanjiang, Liang Huanhuan. An improved DV-Hop localization for wireless sensor networks[J]. Chinese Journal of Sensors and Actuators, 2011, 24(1): 83-87. DOI:10.3969/j.issn.1004-1699.2011.01.018 |
| [13] |
Lee S W, Lee D Y, Lee C W. Enhanced DV-Hop algorithm with reduced hop-size error in Ad hoc networks[J]. IEICE Transactions on Communications, 2011, 94(7): 2130-2132. |
| [14] |
Tomic S, Mezei I. Improvements of DV-Hop localization algorithm for wireless sensor networks[J]. Telecommunication Systems, 2016, 61(1): 93-106. DOI:10.1007/s11235-015-0014-9 |
| [15] |
Haidar S. A novel localization algorithm for large scale wireless sensor networks[J]. Computer Communications, 2014, 45(1): 32-46. |
| [16] |
Kumar S, Lobiyal D K. An advanced DV-Hop localization algorithm for wireless sensor networks[J]. Wireless Personal Communications:an International Journal, 2013, 71(2): 1365-1385. |
| [17] |
Manisekaran S V, Venkatesan R. Cluster-based architecture for range-free localization in wireless sensor networks[J]. International Journal of Distributed Sensor Networks, 2014, 1-9. |
| [18] |
Gui Linqing, Val T, Wei A, et al. Improvement of range-free localization technology by a novel DV-hop protocol in wireless sensor networks[J]. Ad Hoc Networks, 2015, 24(PB): 55-73. |
| [19] |
Xu Yang, Luo Xiong, Wang Weiping, et al. Efficient DV-HOP localization for wireless cyber-physical social sensing system:a correntropy-based neural network learning scheme[J]. Sensors, 2017, 17(1): 135. |
| [20] |
Gumaida B F, Luo J. An efficient algorithm for wireless sensor network localization based on hierarchical structure poly-particle swarm optimization[J]. Wireless Personal Communications, 2017, 97(1): 125-151. |
| [21] |
Banihashemian S S, Adibnia F, Sarram M A. A new range-free and storage-efficient localization algorithm using neural networks in wireless sensor networks[J]. Wireless Personal Communications, 2018, 98(1): 1547-1568. |
| [22] |
Erdemir E, Tuncer T E. Path planning for mobile-anchor based wireless sensor network localization:static and dynamic schemes[J]. Ad Hoc Networks, 2018, 77(8): 1-10. |
| [23] |
Gumaida B F, Luo J. ELPMA:efficient localization algorithm based path planning for mobile anchor in wireless sensor network[J]. Wireless Personal Communications, 2018, 100(3): 721-744. |
| [24] |
Gui Linqing, Zhang Xiaorong, Ding Quan, et al. Reference anchor selection and global optimized solution for DV-Hop localization in wireless sensor networks[J]. Wireless Personal Communications, 2017, 96(4): 5995-6005. DOI:10.1007/s11277-017-4459-x |
| [25] |
Eren T, Goldenberg O K, Whiteley W, et al.Rigidity, computation, and randomization in network localization[C]//Proceedings of IEEE INFOCOM.HongKong: IEEE, 2004: 2673-2684.
|
| [26] |
Huang B Q, Yu C B, Anderson B D O.Connectivity-based distance estimation in wireless sensor networks[C]//Proceedings of 2010 IEEE Global Telecommunications Conference.Miami: IEEE, 2010: 1-5.
|
| [27] |
Wang Y, Gao J, Mitchell J S B.Boundary recognition in sensor networks by topological methods[C]//Proceedings of the 12th Annual International Conference on Mobile Computing and Networking.New York: ACM, 2006: 122-133.
|


