2. 北京市融合网络与泛在业务工程技术研究中心, 北京 100083;
3. 中国移动通信集团设计院有限公司, 北京 100080
针对车联网中车辆间相遇机会间隔的统计分布模型及其参数估计问题,基于北京市出租车轨迹大数据,提出了基于栅格划分和地理哈希值索引的过滤查找方法和轨迹内插方法以高效提取车辆间的相遇机会时刻,进而对机会间隔进行统计建模、参数估计和假设检验.模型呈现分段分布,在小尺度时间间隔上呈指数分布,在大尺度间隔上呈对数正态分布,并具有重尾特征.
2. Beijing Engineering and Technology Research Center for Convergence Networks and Ubiquitous Services, Beijing 100083, China;
3. China Mobile Group Design Institute Co., Ltd., Beijing 100080, China
As a kind of opportunistic networks, the vehicle network, in which vehicles communicate instantaneously with each other only when they meet opportunely, attracts more and more attentions. The inter-contact times of communication opportunities depend on the factors such as the vehicle moving model and the vehicle density. Based on the data of the taxi traces in Beijing city, an efficient method which combines the GeoHash-based filter and the trace interpolation is proposed to extract all the instants of the communication opportunities to model the statistical distribution. It is concluded that the inter-contact times obey an exponential distribution if the interval is small while a log-normal one if the interval is large. Such a piecewise heavy-tailed distribution will affect the design of the vehicle networks to some extent.
车联网[1]以具有智能信息处理、无线通信和定位能力的车辆为主要组成单元,通过传感技术、通信技术和数据处理技术等实现车辆、乘车人和道路基础设施等实体的互联互通,服务于车辆行驶安全、交通规划控制和移动信息服务等应用.车联网属于机会网络[2-3]的一类.受限于车辆无线通信的最大距离,车辆和车辆之间或车辆与道路基础设施之间通常无法建立长时间的通信链路,车联网的通信主要依赖于两车接近时所形成的瞬间通信机会.通信机会的研究是车联网的基础性问题之一.其中,通信机会时间间隔(inter-contact times)[4]是衡量通信机会的重要指标之一,指车辆两次相邻的通信机会间的时间长度,它对车联网中的移动模型和仿真方案、转发策略、路由机制及网络容量等都有很大影响[5-8].
通信机会时间间隔受到节点移动行为、节点疏密程度、道路地理分布、无线通信可达半径等多方面因素的影响,其统计分布相当复杂.目前在车载网络通信机会的研究领域主要有2类方法,即基于模型和基于实证数据.
在基于模型的研究中,需要首先考虑节点的移动行为模型.目前主要有3类经典的独立同分布移动模型,即随机路点移动模型(RWP, random waypoint mobility model)[9]、随机步长模型(RWM, random walk mobility model)[10]、随机方向移动模型(RDM, random direction mobility model)[11]. Carofiglio等[12-13]基于RWP模型指出移动点相遇时间间隔服从指数分布. Cai等[14]基于RWP和RWM模型,证明在一个有限边界的移动空间中节点相遇时间间隔服从指数分布,但如果去掉边界条件则服从近似幂律分布.节点间的社会关系也对节点移动和相遇模型存在影响[15].
理论模型与实际的车辆运动存在一定的差异,不少学者通过收集实际数据集开展实证研究. Chaintreau等[16-18]通过分析实际数据集中人类移动模型,提出节点相遇时间间隔服从近似的幂律分布. Zhang等[19]指出按固定线路的公交车相遇时间间隔大体符合混合的正态分布. Zhu等[20]则利用上海市出租车轨迹数据证明出租车相遇时间间隔近似服从指数分布. Li等[21]统计分析了北京公交车的数据,发现相遇时间间隔概率分布呈现三段式结构,其中中间一段服从幂律分布,只有最后一段服从指数分布.此外,车辆相遇时间也被作为广义社会行为进行了研究[22].
总体上,现有研究从模型和实证的不同角度揭示了车辆相遇时间间隔规律,然而前者的移动行为模型的假设条件过于理想,与实际系统存在差异,而后者归纳的概率分布模型结论也并非完全一致,对车辆密度对概率分布参数的影响也缺乏细致考察.
基于2010年5月北京市出租车的经纬度轨迹数据,考察不同车辆密度条件下和不同区间分段上的车辆相遇机会间隔的统计分布,提出采取分段分布的方式刻画车辆相遇时间的统计分布,并强调了实证数据中出现的重尾分布及其对车联网研究的影响,为完善现有车联网的研究提供模型支撑.
1 数据处理过程出租车轨迹数据需要进行预处理和相遇时刻提取,获取车载网络通信机会的间隔数据,进而进行统计分析.
1.1 数据预处理为提升数据分析质量,首先需要对原始数据进行预处理.
由于部分车载定位设备工作不稳定,导致个别车辆的个别时间段的数据缺失,对后续挖掘造成了较大影响,所以需对数据进行清洗,对记录数据为空的车辆进行剔除.
原始数据由多个表格和文件构成,不便处理.需将多个数据源中的数据进行汇总,添加车辆的唯一编号信息,形成规范记录格式的单一数据源.每条记录包含4个字段,分别是车辆编号、采样时刻、经度坐标和纬度坐标.其中采样时刻周期Ts=10s.记所有记录的集合为R,若车辆数为Nv,每辆车的记录数为Nt,则总的记录数为N=NvNt.
1.2 相遇时刻提取算法假设车载无线通信的有效距离为dc,直接查找所有两两处于有效通信范围的记录对的时间复杂度为O(N2),算法效率较低.
为了高效且准确地计算相遇时间间隔,提出基于地理哈希编码(GeoHash)[23]和线性车辆轨迹插值的相遇时刻提取算法.
将所考虑的地理区域划分为若干个正方形区域,称为栅格,所有栅格的集合记为G.每个栅格可计算其地理哈希值,此哈希值是该栅格范围内的所有地理坐标所映射的唯一码串,同一栅格内所有的地理位置具有相同的哈希值.记哈希函数为f,则对任意栅格g∈G,有唯一地理哈希值h=f(g)与之对应.通过选择合理的栅格尺度和哈希值计算方式,确保栅格与其地理哈希值构成一一映射关系,记所有栅格的地理哈希值集合为H=f(G).
随后,对时刻t,建立地理哈希值和轨迹记录间的索引表,可通过该索引获得时刻t地理哈希值为h的栅格中所有的车辆轨迹记录
记栅格边长为ds,则中心栅格车辆和处于它相邻8个栅格内的车辆距离不大于
|
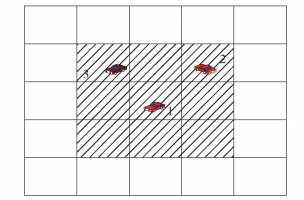
图 1 栅格划分示意 |
因此,根据t时刻轨迹记录是否隶属于相同或近邻的栅格,可以初步确定可能相遇的节点.建立索引表的时间复杂度是O(N).对每个索引键(h, t)∈HT,记N(h)是地理哈希值h对应栅格的相邻栅格(含自身)的地理哈希值集合,则
| $ S^{\prime}=\bigcup\limits_{k \in N(h)} \lambda(k, t) $ |
表示h对应栅格及其周围栅格在t时刻的所有记录,此时仅需要检查集合S=λ(h, t)和集合S′是否存在车辆相遇的情况.基于地理哈希值的过滤算法只需要筛选所在和邻近栅格的车辆.当总栅格数量非常大时,本算法仅检查所在和邻近的9个栅格,如图 1所示,若筛选1号车与其他车可能的相遇情况时,只搜索该时刻该车所在的栅格和该栅格邻近栅格中的车辆记录,因此可以显著降低数据处理时间.
在初步筛选出可能相遇的车辆对之后,还需要进一步确定它们是否相遇以及在何时相遇.由于在两次采样间隔内没有车辆轨迹数据,所以需要通过内插算法估计车辆轨迹,确定车辆间的相遇事件.采用的方法为三维空间(经度、纬度、时间)的线性插值法,并对本格和邻近格内的车辆进行穷举遍历,获得产生通信机会的车辆(组)和相遇时刻.
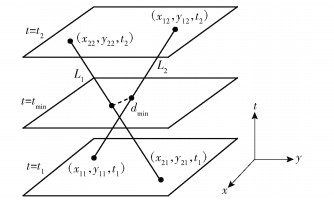
考虑车辆q1和q2,令其可能的相遇时刻为t.基于线性插值算法确定两车最近距离的过程如图 2所示.图中x轴为经度,y轴为纬度,t轴为时间,已知车辆q1在时刻t1的坐标为(x11, y11, t1),在时刻t2的坐标为(x12, y12, t2);车辆q2在t1时刻的坐标为(x21, y21, t1),在t2时刻的坐标为(x22, y22, t2),通过线性插值,得到在该时间段两车的轨迹分别为L1和L2.
| $ L_{1} :\left\{\begin{array}{l}{x_{L_{1}}(t)=\frac{\left(x_{12}-x_{11}\right)\left(t-t_{1}\right)}{t_{2}-t_{1}}+x_{11}} \\ {y_{L_{1}}(t)=\frac{\left(y_{12}-y_{11}\right)\left(t-t_{1}\right)}{t_{2}-t_{1}}+y_{11}}\end{array}\right. $ | (1) |
| $ L_{2} :\left\{\begin{array}{l}{x_{L_{2}}(t)=\frac{\left(x_{22}-x_{21}\right)\left(t-t_{1}\right)}{t_{2}-t_{1}}+x_{21}} \\ {y_{L_{2}}(t)=\frac{\left(y_{22}-y_{21}\right)\left(t-t_{1}\right)}{t_{2}-t_{1}}+y_{21}}\end{array}\right. $ | (2) |
|
图 2 两车运动轨迹线性插值示意 |
在任意时间t∈[t1, t2],两车的距离为
| $ d(t)=\sqrt{\left(x_{L_{1}}(t)-x_{L_{2}}(t)\right)^{2}+\left(y_{L_{1}}(t)-y_{L_{2}}(t)\right)^{2}} $ | (3) |
将d(t)对时间t求导并令导数为0,记满足条件的时刻为t′,则t′时刻即为两车距离最近的时刻.考虑时间范围[t1, t2],所以当t′属于[t1, t2]时,说明t′时刻即为该时段内两车距离最近的时间点.否则,两车距离最近的时间点将出现在区间端点t1或t2,此时分别计算两车在区间端点时刻的距离,取最小值记为min [d(t1), d(t2)],最终可得到该时间范围两车距离最近的时间点tmin和最近距离dmin.上述各种情形总括如下:
| $ t_{\min }=\left\{\begin{array}{ll}{t^{\prime}, } & {t^{\prime} \in\left[t_{1}, t_{2}\right]} \\ {t_{1}, } & {t^{\prime} \in\left[t_{1}, t_{2}\right] \wedge d\left(t_{1}\right)=\min \left[d\left(t_{1}\right), d\left(t_{2}\right)\right]} \\ {t_{2}, } & {t^{\prime} \in\left[t_{1}, t_{2}\right] \wedge d\left(t_{2}\right)=\min \left[d\left(t_{1}\right), d\left(t_{2}\right)\right]}\end{array}\right. $ | (4) |
| $ d_{\min }=d\left(t_{\min }\right) $ | (5) |
其中若dmin≤dc,说明两车在此时段相遇,且tmin为相遇时间点,否则说明两车在此时段不相遇.上述插值算法较精确地找出了车联网中的相遇时间间隔,弥补了车辆轨迹数据在两个采样时间内的空缺.
1.3 机会间隔分析和拟合优度检验假设某辆车在行驶过程中,不断和其他车辆相遇,相遇时刻的序列为{t1, t2, …, tk, …},计算其差分{t2-t1, t3-t2, …, tk+1-tk, …}为通信机会间隔序列.根据得到的所有车辆的通信机会间隔序列,可以分析车辆通信机会的时间间隔的概率分布模型,并进行拟合优度检验.
采用Kolmogorov Smirnov检验(简称KS检验)比较假设分布的分布函数和样本的累积概率函数,若置信度为0.95的p值大于等于0.05时,则接受假设.
2 机会间隔统计模型及分析将车辆区域限定在东经116.178~116.576°,北纬39.74~40.05°的矩形范围内,此范围包含了北京市的大部分区域.设通信范围dc=100m,若考虑城市快速道路车速可达100km/h,故栅格大小设为ds=700m.
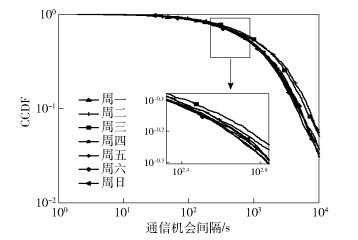
2.1 固定车辆密度条件下的机会间隔模型首先,以一天为总的统计范围(0:00—24:00),随机抽取100辆车,对其通信机会间隔进行概率分布建模.图 3即为一周7d的通信机会间隔的互补累计分布函数(CCDF,complementary cumulative distribution function),可以看出周一~周日的通信机会间隔分布相似.
|
图 3 一周通信机会间隔CCDF曲线对比 |
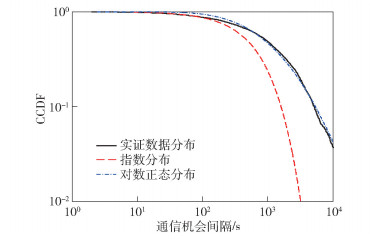
由于不同日期的通信机会间隔统计分布相似,现仅考虑(2010年5月某周)周一的24h数据作为代表进行具体研究.在所有车辆中随机抽取100辆出租车为研究对象,仅考虑这100辆车构成子集间的通信机会.该子集中的车辆机会间隔的CCDF曲线如图 4所示.图中指数分布和对数正态分布的曲线拟合度较高,但均不能在大尺度范围上完美描述整体统计分布情况.指数分布适合描述通信机会间隔较小的情况,对数正态分布适合描述通信机会间隔较大的情况.
|
图 4 拟合曲线对比(0~10000s) |
基于KS假设检验方法,对数据进行多次抽样分析和检验后,可认为在上述实验条件下机会间隔模型属于某种分段的统计分布.
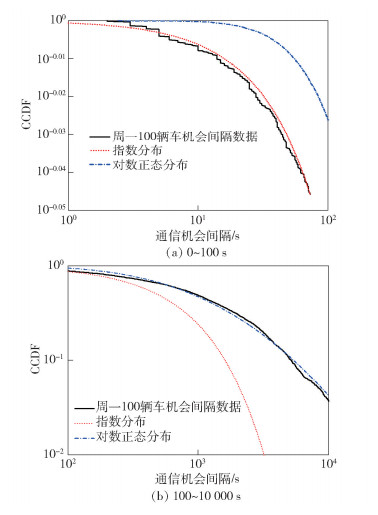
根据实测数据,大体上可将通信机会时间间隔分为两段,在小尺度间隔上和大尺度间隔上通信机会时间间隔服从不同的分布.两段的分界点不是固定和明确的,一方面该分界点的取值受到具体数据中多种因素的影响;另一方面分界点两侧的概率分布变化并不是突变的,而是渐变的.根据实际数据的分析,以100s作为分界点是较为合理的,当机会间隔在0~100s时,其概率分布服从指数分布,如图 5(a)所示,KS检验结果p值平均为0.5,可接受该假设.当机会间隔在100~10000s时,其概率分布服从对数正态分布,如图 5(b)所示,KS检验结果p值平均为0.7,可接受该假设.
|
图 5 分段概率分布拟合曲线对比 |
相比指数分布,对数正态分布是一种重尾分布,表明通信机会间隔取非常大数值的概率不可忽视.实际场景中,此结论表明存在一定概率,使得某部车辆在很长的时间中都没有和其他车辆的通信机会,这对网络时延、路由协议、缓存设计等提出了更严峻的挑战.
2.2 不同车辆密度条件的机会间隔模型车联网的车辆密度对机会间隔有一定的影响.若从总体中选取不同数量的车辆子集,由于研究区域不变,等价于车联网中车辆密度发生改变.本节定义的车辆密度z为单位面积上的车辆数量,且设所研究区域为1个单位面积.
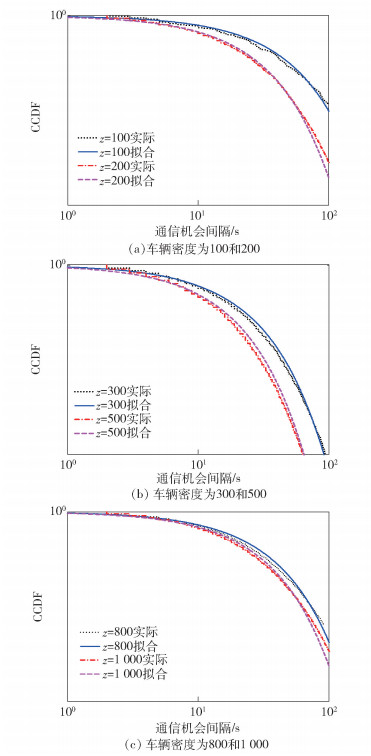
分别建立车辆密度z为100、200、300~1000等不同条件下的统计模型,探讨模型与车辆密度间的数学联系.当相遇时间间隔在0~100s内时,不同车辆密度的统计模型可以用不同参数的指数分布进行拟合,如图 6所示,拟合的指数分布参数均通过KS检验,拟合情况良好.
|
图 6 拟合指数曲线对比(0~100s) |
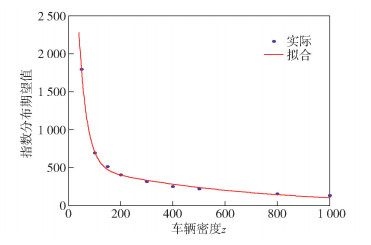
车辆密度为50~1000时,指数分布对应的分布参数的曲线如图 7所示.注意到负指数分布随机变量的数学期望为λ-1.当车辆密度增大时,指数分布的参数增大,数学期望降低,平均等待下一次通信机会的间隔时间变小.因此,更大的车辆密度有利于寻找更多的通信机会和降低通信机会间隔.
|
图 7 不同车辆密度机会间隔拟合指数分布系数曲线 |
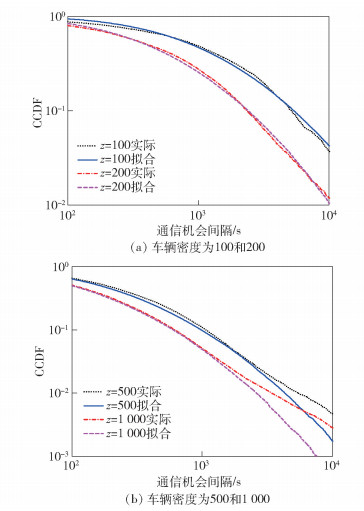
当机会间隔在100~10000s时,根据数据的实证分析,在车辆密度为100或200时,对数正态分布的拟合良好.当车辆密度更大时实际机会间隔在1000s后偏离对数正态分布,表明随着车辆密度的增大,分段分布产生了一定的偏离,如图 8所示.分布在尾部的统计数据较对数正态分布进一步增加,表明重尾分布程度更为严重,同时在形态上接近幂律,这一方面会对车载网络协议设计带来更大的影响,另一方面也提示在建模过程中需要更多的分段来精确拟合实际的数据统计分布.目前考虑的分段区间最大为10000s,基本可以满足大部分情况下车载网的研究需求.
|
图 8 拟合对数正态曲线对比(100~10000s) |
通信机会间隔分布是车联网的重要指标之一.现有的研究结论存在不一致的地方,同时对车辆密度对通信机会间隔分布的影响缺乏研究.基于北京市出租车轨迹数据,提出了基于栅格划分和地理哈希值索引过滤查找方法以提取车辆间的相遇机会时刻,提出线性插值的方式较为精确地估计相遇时刻,为高效处理车辆轨迹数据提供了算法支持.随后对机会间隔进行了统计建模和假设检验,建立了对车联网中相遇时间间隔概率分布的统计模型,并重点考虑了模型随车辆密度的变化情况.
研究表明,车联网中通信机会间隔概率分布可建模为分段模型.大体上,在相遇时间间隔在0~100s时,机会间隔服从指数概率分布,且随着车辆密度增加,指数分布的数学期望呈下降趋势;当相遇时间间隔在100~10000s时,若车辆密度较小时,机会间隔服从对数正态概率分布,但随着车辆密度的增大,其分布与对数正态分布曲线存在一定的偏离.单一的指数分布或对数正态分布不能完整表征不同通信机会间隔尺度下的统计分布.同时也指出通信机会间隔的分布尽管在短时期上呈现指数分布,但是在长期分布上有一定的重尾特征.
车联网的通信机会间隔受到车辆移动模型、车辆密度、车辆速度、道路地理位置等多种因素的影响,然而现有的研究对各影响参数的研究有限.提出的实证结论提供了更为细致的统计模型和分析,进一步丰富了车联网中关于通信机会间隔模型的研究成果.
| [1] |
Zhang Weiwei, Xi Xiaoqiang. The innovation and development of internet of vehicles[J]. China Communications, 2016, 13(5): 122-127. DOI:10.1109/CC.2016.7489980 |
| [2] |
Cheng Jiujun, Cheng Junlu, Zhou Mengchu, et al. Routing in internet of vehicles:a review[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(5): 2339-2352. DOI:10.1109/TITS.2015.2423667 |
| [3] |
Alam K M, Saini M, ElSaddik A. Toward social internet of vehicles:concept, architecture, and applications[J]. IEEE Access, 2015(3): 343-357. |
| [4] |
Hernández-Orallo E, Cano J C, Calafate C T, et al. New approaches for characterizing inter-contact times in opportunistic networks[J]. Ad Hoc Networks, 2016, 52: 160-172. DOI:10.1016/j.adhoc.2016.04.003 |
| [5] |
熊永平, 孙利民, 牛建伟, 等. 机会网络[J]. 软件学报, 2009, 20(1): 124-137. Xiong Yongping, Sun Limin, Niu Jianwei, et al. Opportunistic networks[J]. Journal of Software, 2009, 20(1): 124-137. |
| [6] |
李静林, 刘志晗, 杨放春. 车联网体系结构及其关键技术[J]. 北京邮电大学学报, 2014, 37(6): 95-100. Li Jinglin, Liu Zhihan, Yang Fangchun. Internet of vehicles:the framework and key technology[J]. Journal of Beijing University of Posts and Telecommunications, 2014, 37(6): 95-100. |
| [7] |
Dede J, Förster A, Hernández-Orallo E, et al. Simulating opportunistic networks:survey and future directions[J]. IEEE Communications Surveys & Tutorials, 2018, 20(2): 1547-1573. |
| [8] |
Le T, Gerla M. Time-constrained anycast routing under short contact duration in delay-tolerant networks[J]. Annals of Telecommunications, 2018, 73(9-10): 549-558. DOI:10.1007/s12243-018-0657-0 |
| [9] |
Conti M, Giordano S, May M, et al. From opportunistic networks to opportunistic computing[J]. Communications Magazine, 2010, 48(9): 126-139. DOI:10.1109/MCOM.2010.5560597 |
| [10] |
Pramanik A, Choudhury B, Choudhury T S, et al.Simulative study of random waypoint mobility model for mobile Ad hoc networks[C]//Global Conference on Communication Technologies.Nagercoil, Tamil Nadu: IEEE, 2015: 112-116.
|
| [11] |
Zhang Jinbei, Fu Luoyi, Tian Xiaohua, et al. Analysis of random walk mobility models with location heterogeneity[J]. IEEE Transactions on Parallel and Distributed Systems, 2015, 26(10): 2657-2670. DOI:10.1109/TPDS.2014.2361458 |
| [12] |
Carofiglio G, Chiasserini C F, Garetto M, et al. Route stability in MANETs under the random direction mobility model[J]. IEEE Transactions on Mobile Computing, 2009, 8(9): 1167-1179. DOI:10.1109/TMC.2009.20 |
| [13] |
Sharma G and Mazumdar R.Scaling laws for capacity and delay in wireless ad hoc networks with random mobility[C]//2004 IEEE International Conference on Communications, Paris: IEEE, 2004: 3869-3873.
|
| [14] |
Cai H, Eun D Y.Crossing over the bounded domain: from exponential to power-law inter-meeting time in manet[C]//Proceedings of the 13th Annual ACM International Conference on Mobile Computing and Networking.New York: ACM, 2007: 159-170.
|
| [15] |
Yuan Peiyan, Yu Hai, Liu Ping.User contact behavior analysis: a social relationship perspective[C]//Proceedings of the 11th EAI International Conference on Mobile Multimedia Communications.Brussels: ICST, 2018: 143-152.
|
| [16] |
Chaintreau A, Hui P, Crowcroft J.Impact of human mobility on the design of opportunistic forwarding algorithms[C]//The 25th IEEE International Conference on Computer Communications.Barcelona: IEEE, 2006: 1-13.
|
| [17] |
Hui P, Chaintreau A, Scott J, et al.Pocket switched networks and human mobility in conference environments[C]//Proceedings of the 2005 ACM SIGCOMM Workshop on Delay-Tolerant Networking.New York: ACM, 2005: 244-251.
|
| [18] |
Henderson T, Kotz D, Abyzov I.The changing usage of a mature campus-wide wireless network[C]//Proceedings of the 10th Annual International Conference on Mobile Computing and Networking.New York: ACM, 2008: 187-201.
|
| [19] |
Zhang Xiaolan, Kurose J, Levine B N, et al.Study of a bus-based disruption-tolerant network: mobility modeling and impact on routing[C]//Proceedings of the 13th Annual ACM International Conference on Mobile Computing and Networking.New York: ACM, 2007: 195-206.
|
| [20] |
Zhu Hongzi, Li Minglu, Fu Luoyi, et al. Impact of traffic influxes:revealing exponential intercontact time in urban vanets[J]. Parallel and Distributed Systems, 2011, 22(8): 1258-1266. DOI:10.1109/TPDS.2010.176 |
| [21] |
Li Yong, Jin Depeng, Hui Pan, et al.Revealing contact interval patterns in large scale urban vehicular ad hoc networks[C]//Proceedings of the ACM SIGCOMM 2012 Conference On Applications, Technologies, Architectures, and Protocols For Computer Communication.New York: ACM, 2012: 299-300.
|
| [22] |
Karsai M, Jo H H, Kaski K.Empirical findings in human bursty dynamics[C]//Bursty Human Dynamics.Cham, Switzerland: Springer, 2018: 31-46.
|
| [23] |
Gao Meng, Xiang Longgang, Gong Jianya.Organizing large-scale trajectories with adaptive Geohash-tree based on secondo database[C]//2017 25th International Conference on Geoinformatics.Buffalo: IEEE, 2017: 1-6.
|


