2. 南京信息工程大学 物理与光电工程学院, 南京 210044
针对使用概率成形技术和高阶调制格式的变速率光传输系统,提出了一种基于四次方特征值的盲调制格式识别方法.该方法利用接收端信号经过四次方运算后的快速傅里叶变换(FFT)峰值和方差值,能够实现偏振复用概率成形高阶调制格式的精确识别.在联合仿真平台上搭建了高速长距离相干光传输系统,验证了新方法的有效性.
2. Institute of Optoelectronics, Nanjing University of Information Science and Technology, Nanjing 210044, China
A blind modulation format identification method based on fourth-power eigenvalues is proposed for variable-rate optical transmission systems employing probabilistic shaping technology and high-order modulation formats. By using the fast Fourier transformation (FFT) peak value and variance after the received signal passes through fourth-power operation, accurate identification of high order modulation formats with probabilistic shaping and polarization multiplexing can be realized. A high-speed long-haul coherent optical transmission system is built on the platform of the joint simulation to verify the effectiveness of the method.
随着高清视频、4K电视、移动互联网等技术的飞速发展,全球网络流量迅速增长,日益增长的带宽需求对作为信息互联互通管道基石的大容量长距离骨干网提出了越来越高的要求.光纤通信系统正向超高速率、超长距离、超大容量和超高频谱效率的方向发展.如何最大程度地提高单信道的传输承载能力,使之接近香农限成为国内外学者研究的热点.
为了追求更高的传输速率,正交相移键控(QPSK, quadrature phase shift keying)、16进制正交幅度调制(QAM,quadrature amplitude modulation)、64QAM等高阶调制格式已被广泛用于提高频谱效率的研究.由于光纤信道受到功率的限制,为了在不增加发射功率的情况下提高频谱效率,必须对信号进行优化.信号成形理论指出,在信号满足高斯分布时,信道容量可以达到香农极限.采用信号成形技术能够实现在提高信息传输速率的同时有效地提高频谱效率.概率成形(PS,probabilistic shaping)技术通过让能量低的符号比能量高的符号出现的次数更多,使其信号呈高斯分布,将概率成形技术运用到16QAM、64QAM等高阶调制格式中,能显著提高传输容量和频谱效率,可明显改善光通信系统的性能[1-3].
目前网络流量变得越来越动态化和不可预测,使得光传输网络正在从传统的固定光网络向下一代灵活认知网络发展.通过在收发机使用动态带宽分配和灵活的调制格式,可以实现可变线路速率传输,在这种情况下,调制格式识别(MFI,modulation format identification)对于信号的解调和恢复在接收机中是必不可少的.目前很多调制格式识别技术已经被提出[4-6],而这些算法存在噪声容忍度差、算法复杂度高等问题,并且都是针对传统均匀分布的QPSK、16QAM、64QAM等信号进行识别,因此需要提出适用于概率成形光传输系统的调制格式识别方法来满足未来变速率光传输系统的发展需求.
针对使用概率成形技术的光传输系统,笔者提出了一种基于接收端信号四次方运算后的FFT峰值和方差值的盲调制格式识别方法.利用Matlab和VPI软件搭建了28GBaud偏振复用相干光传输仿真系统平台,分别计算了6种调制格式在不同信噪比条件下的识别准确率,验证了该方法的有效性.
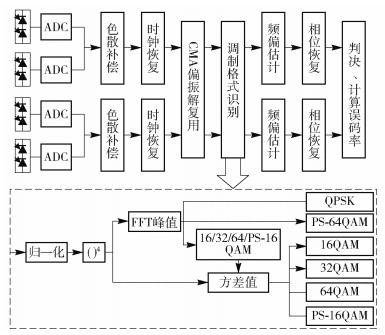
1 概率成形信号的调制格式识别调制格式识别系统框图如图 1所示.针对相干光通信系统,在图 1所示的接收机数字信号处理(DSP,digital signal processing)结构中,对模数转换(ADC,analog-to-digital conversion)后的接收信号首先进行色散补偿、时钟恢复和恒模算法(CMA,constant modulus algorithm)偏振解复用,这些数字信号处理都与调制格式无关;然后再进行MFI,经过MFI成功估计输入信号的调制格式后,再进行与调制格式相关的后端数字信号处理.只有正确识别出调制格式,才能成功进行频偏估计和载波恢复,最终实现QAM信号解调.
|
图 1 适用于概率成形信号的调制格式识别系统框图 |
在传统的光纤传输系统中,QAM信号星座图中的每个点都以相同的概率传输,无法使信道容量接近香农极限.通过概率成形让能量低的符号比能量高的符号出现的次数更多,从而降低发射功率,这种非均匀分布会降低发射机输出的熵,使用相同能量可以传输更多信号.在功率受限系统中,概率成形方法能提高对非线性效应和噪声的容忍度.对于给定的平均比特率或者固定的传输熵,要使平均传输能量最小化的最优分布是让星座点服从麦克斯韦玻尔兹曼分布,从而在加性高斯白噪声(AWGN,additive white Gaussian noise)信道中实现最大信息速率.
对于一个输入AWGN离散信道的信号x={x1, x2, …, xm}来说,其每个星座点出现的概率密度函数P可用麦克斯韦-玻尔兹曼函数表示为
| $ P\left( {{x_i}} \right) = \frac{1}{{\sum\limits_{k = 1}^m {{{\rm{e}}^{-vx_k^2}}} }}{{\rm{e}}^{-vx_i^2}} $ | (1) |
其中:v为一个在0~1之间取值的标量,它可以保证所有信号星座点出现的概率之和为1,也代表了概率成形的程度. v越大,表示发射机信源熵值越低,信号星座概率成形的程度越大.对于16QAM信号来说,当v取0.2时,16个星座点的概率密度函数为
| $ P\left( {{x_i}} \right) = \left| {\begin{array}{*{20}{c}} {0.007\;1}&{0.034\;9}&{0.034\;9}&{0.007\;1}\\ {0.034\;9}&{0.173\;1}&{0.173\;1}&{0.034\;9}\\ {0.034\;9}&{0.173\;1}&{0.173\;1}&{0.034\;9}\\ {0.007\;1}&{0.034\;9}&{0.034\;9}&{0.007\;1} \end{array}} \right| $ | (2) |
在接收端,将接收到的四路偏振复用QAM信号XI、XQ、YI、YQ合并为2个偏振态上的复数信号,然后分别进行色散补偿、时钟恢复和CMA偏振解复用后进入调制格式识别模块.提出的调制格式识别方法既可以用X偏振态信号,也可以用Y偏振信号来进行识别,并且调制格式识别过程中得到的四次方FFT频谱也可用于后续频偏估计,无需引入额外复杂度.
首先,为了保持特征值的一致性,需要对信号进行功率归一化操作,然后对输入信号进行四次方运算,在快速傅立叶变换(FFT,fast Fourier transformation)后,信号会在其幅度谱上表现出一条峰值谱线,FFT谱的峰值可以表示为
| $ {4^{{\rm{th}}}}-{\rm{FF}}{{\rm{T}}_{\max }} = \frac{{\max \left| {\sum\limits_{k = 0}^{N-1} {{r^4}\left( k \right){{\rm{e}}^{-{\rm{j}}2\pi \Delta fT}}} } \right|}}{N} $ | (3) |
其中:r(k)为第k个接收到的信号,T为符号的持续时间,N为符号长度.对于任意的调制格式,有
| $ r\left( t \right) = \sum {\sqrt E \left( {{a_k} + {\rm{j}}{b_k}} \right)p\left( {t-kT} \right){{\rm{e}}^{{\rm{j}}\Delta \theta }} + n\left( t \right)} $ | (4) |
其中:E为信号的能量, Δθ为载波相位偏差, n(t)为零均值复高斯白噪声,ak、bk分别代表了QAM信号的实部和虚部.将调制光信号看成一个平稳随机过程,对于一个零均值复平稳随机过程S(t),其p阶混合矩阵可以表示为
| $ {\mathit{\boldsymbol{M}}_{p, q}} = E\left\{ {{{\left[{S\left( t \right)} \right]}^{p - q}}{{\left[{{S^*}\left( t \right)} \right]}^q}} \right\} $ | (5) |
其中S*(t)是S(t)的共轭, 四阶累计量为[7]
| $ {C_{40}} = {M_{40}}-3{\left( {{M_{20}}} \right)^2} = {4^{{\rm{th}}}}-{\rm{FF}}{{\rm{T}}_{\max }} $ | (6) |
QPSK/16QAM/32QAM/64QAM/PS-16QAM/PS-64QAM信号理论上的四次方FFT峰值如表 1所示.
|
|
表 1 不同调制格式的四次方FFT峰值 |
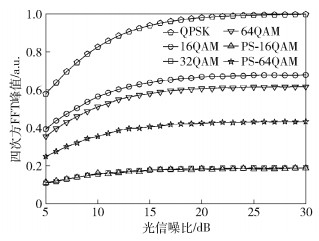
使用Matlab软件对这几种不同调制格式的四次方FFT峰值和信噪比之间的关系进行了仿真,如图 2所示.可以看出,QPSK/PS-64QAM的FFT峰值和其他调制格式有明显区别,很容易就可以通过阈值的设置进行识别,但是16QAM/64QAM和32QAM/PS-16QAM的FFT峰值很接近,难以区分,因此需要进行细估计.
|
图 2 四次方FFT峰值和信噪比的关系 |
根据式(7),对这4种调制格式信号进行四次方后分别计算其方差值,如表 2所示.
| $ {4^{{\rm{th}}}}-{\rm{Var}}. = \frac{{\sum\limits_{k = 1}^N {\left( {\left| {{r^4}\left( k \right)} \right|-\overline {{r^4}\left( k \right)} } \right)} }}{N} $ | (7) |
|
|
表 2 不同调制格式的四次方方差 |
可以看出32QAM/PS-16QAM的四次方方差值差异明显,可以很好地进行区分,16QAM/64QAM方差的差别也远大于它们四次方FFT峰值的差距,因此也可以用方差来进行识别.
同样使用Matlab软件对这4种调制格式的四次方方差值和信噪比之间的关系进行了仿真,如图 3所示.根据仿真结果,所提出的方法中32QAM/PS-16QAM四次方方差判决阈值设为4.940 9,16QAM/64QAM判决方差阈值设为1.655 2.

|
图 3 四次方方差值和光信噪比的关系 |
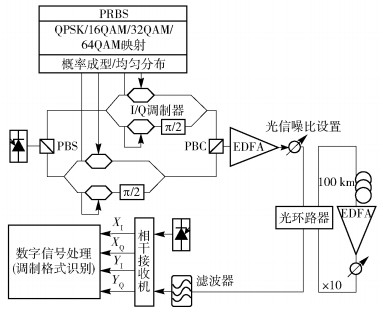
为了验证算法的有效性,笔者用Matlab和VPI软件搭建了28 GBaud/s PDM-QAM相干光传输系统,如图 4所示.
|
图 4 调制格式识别系统验证仿真框图 |
在发射端,首先激光器产生1 550 nm的连续光经过偏振分束器(PBS,polarization beam splitter)分别进入2个调制器,将二进制伪随机序列(PRBS,pseudo-random binary sequence)进行QAM映射得到QPSK/16QAM/32QAM/64QAM信号,使用式(1)中的概率密度函数进行概率成形,PS-16QAM信号的v取0.2,PS-64QAM信号的v取0.02. QAM信号的实部和虚部分别进入IQ调制器两臂,将2个IQ调制器的输出光信号使用一个偏振合束器(PBC,polarization beam combiner)进行合束,这样就得到了偏振复用的QPSK/16QAM/32QAM/64QAM/ PS-16QAM/PS-64QAM信号,将其经过EDFA放大后进入传输链路.传输链路由光环路器、100 km标准单模光纤、EDFA和可调衰减器组成,环路数目设为10,模拟了1 000 km超长距离传输.在接收端光信号经过光滤波器滤波后进入相干接收机和本振光进行混频,得到双偏振态四路信号进行数字信号处理,并使用所提出的算法进行调制格式识别.
使用所提出的算法对QPSK/16QAM/32QAM/ 64QAM/PS-16QAM/ PS-64QAM共6种调制格式的信号进行识别,光信噪比设置范围为5~30 dB,步长为1 dB.每个信噪比条件下每种调制格式存取100组数据,根据识别结果计算其识别准确率.
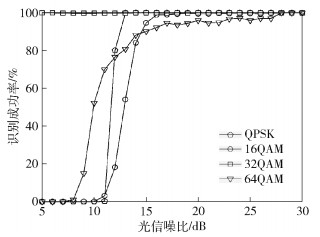
当信噪比为5~30 dB时,使用提出的算法识别均匀分布QPSK/16QAM/ 32QAM/64QAM信号的准确率如图 5所示.可以看出,光信噪比达到15 dB时,这4种调制格式的识别准确率都达到了90%以上.虽然32QAM信号的四次方FFT峰值和PS-16QAM信号很接近,但是与QPSK/16QAM/64QAM的四次方FFT峰值差异较大,并且经过进一步的四次方方差估计可以很容易与PS-16QAM信号进行区分,因此它在低信噪比条件下识别成功率最高.由于16QAM信号的FFT峰值和64QAM较为接近,并且它们的四次方方差值差异相比于其他调制格式也较小,所以虽然进行了进一步的细估计,16QAM/64QAM信号识别成功率的收敛速度要比其他调制格式要差.
|
图 5 均匀分布信号的调制格式识别成功率 |
图 6所示为PS-16QAM/PS-64QAM信号的识别成功率.与32QAM信号相同,由于PS-16QAM四次方方差值和其他调制格式差别较大,低信噪比的识别成功率也很高.同时可以看出,PS-64QAM信号只需四次方FFT峰值即可进行识别,收敛速度较快.通过仿真验证了这种算法在光信噪比达到可靠通信条件阈值前即可有效地对概率成形信号进行识别.

|
图 6 概率成形信号的调制格式识别成功率 |
适用于概率成形高速光传输系统的调制格式识别是未来实现灵活速率光网络非常实际的问题.笔者提出的基于四次方特征值的调制格式识别方法复杂度较低,在低信噪比条件下即可有效识别主流的PS-16QAM/PS-64QAM及传统均匀分布高阶调制格式.仿真结果表明, 光信噪比达到15 dB时,使用本方法的调制格式识别准确率在90%以上.
| [1] |
Fehenberger T, Alvarado A, Bocherer G, et al. On probabilistic shaping of quadrature amplitude modulation for the nonlinear fiber channel[J]. Journal of Lightwave Technology, 2016, 34(21): 5063-5073. DOI:10.1109/JLT.2016.2594271 |
| [2] |
Renner J, Fehenberger T, Yankov M P, et al. Experimental comparison of probabilistic shaping methods for unrepeated fiber transmission[J]. Journal of Lightwave Technology, 2017, 35(22): 4871-4879. DOI:10.1109/JLT.2017.2752243 |
| [3] |
Zhu Y, Li A, Peng W R, et al.Spectrally-efficient single-carrier 400G transmission enabled by probabilistic shaping[C]//Optical Fiber Communications Conference & Exhibition.[S.l.]: IEEE, 2017.
|
| [4] |
Xiang M, Zhuge Q, Qiu M, et al. RF-pilot aided modulation format identification for hitless coherent transceiver[J]. Optics Express, 2017, 25(1): 463. DOI:10.1364/OE.25.000463 |
| [5] |
Isautier P, Pan J, Desalvo R, et al. Stokes space-based modulation format recognition for autonomous optical receivers[J]. Journal of Lightwave Technology, 2015, 33(24): 5157-5163. DOI:10.1109/JLT.2015.2492858 |
| [6] |
Liu G, Proietti R, Zhang K, et al. Blind modulation format identification using nonlinear power transformation[J]. Optics Express, 2017, 25(25): 30895. DOI:10.1364/OE.25.030895 |
| [7] |
Wang Y, Serpedin E, Ciblat P, et al.Non-data aided feedforward cyclostationary statistics based carrierfrequency offset estimators for linear modulations[C]//IEEE Global Telecommunications Conference.[S.l.]: IEEE, 2001.
|


