2. 黄河科技学院 信息工程学院, 郑州 450000
针对超密集网络(UDN)中的上行干扰问题,提出了一种基于多点协作联合接收(JR-CoMP)的分簇与资源分配方法.首先,将用户和基站进行单频段分簇,将同一小小区的多个边缘用户放在不同的用户簇中,将位于相邻小小区并且距离较近的边缘用户放在同一个用户簇中,根据中心用户到已有基站簇的干扰强度将其归簇;然后,对用户簇进行多重子频段分配,为包含同一个小小区用户的多个簇分配不同的子频段,并且尽量为每个用户簇多分配子频段;最后,以最大化系统总传输速率为目标,采用注水算法为每个用户分配功率.仿真结果显示,所提方案能显著提高频谱效率.
2. School of Information Engineering, Huanghe S & T University, Zhengzhou 450000, China
For uplink interference problem in ultra dense networks(UDN), a joint clustering and resource allocation scheme is proposed based on coordinated multiple point joint reception(JR-CoMP). Firstly, users and small base stations are divided into several clusters according to the uni-subband clustering. The multiple edge users in the same small cell are assigned to different user clusters. The users at the close edge of the adjacent small cell are assigned to the same cluster. The cell-center users are clustered according to the interference intensity of them to the existing base station clusters. Then, multi-sub band allocation is performed for user clusters. The user clusters containing the same small cell users are allocated different sub-bands, and the number of allocated sub-bands for each user clusters is as much as possible. Finally, the water-filling algorithm is used to allocate appropriate power to each user with the goal of maximizing the total transmission rate of the system. Simulation results show that spectral efficiency can be significantly improved by the proposed scheme.
超密集网络(UDN, ultra dense networks)是第五代移动通信系统的关键技术之一[1]. UDN在宏基站的覆盖范围内部署大量的小基站.小基站的密集部署使得下行链路和上行链路都存在严重的干扰[2].在下行链路中,小基站之间能够交换信息,通过对信号进行预处理可以消除部分干扰[3],而在上行链路中,用户之间没有信息的交换并且传输天线是全向天线,信号不能沿着期望的方向传输,从而上行链路的干扰更为严重,影响了用户的服务质量,是UDN技术发展的一大障碍.
基于联合接收(JR, joint reception)的多点协作(CoMP, coordinated multiple point)技术通过在协作基站间共享信道状态信息(CSI, channel state information),能减少干扰,提高系统频谱效率[4-5]. Chih-Lin等[6]的研究表明,将JR-CoMP应用于上行链路能增强上行信号,抑制干扰.为了降低JR-CoMP应用于上行链路时的复杂度,Shang等[7]提出了一种与有效天线选择相结合的JR-CoMP方案,以少量的性能损失为代价换取了计算复杂度的显著降低. Li等[8]将小区间干扰协调技术和JR-CoMP技术相结合,提出了JR-CoMP应用于上行链路时的2种信号检测方法.然而,将JR-CoMP直接应用于UDN的上行链路是不可行的,因为UDN中的小基站数量较多,不可能所有的小基站都相互协作[9].为了将JR-CoMP应用于UDN中,有学者提出了将小基站分簇,每个簇包含若干个小基站,每个簇的上行链路采用联合接收[10]. Feng等[11]提出了上行链路的一种动态重叠分簇方案,所有的簇采用相同的频段,也称为全频段分簇,提高了系统的传输速率. Hajisami等[12]提出了一种基于区域的分簇和频段分配方案,将用户分为中心用户和边缘用户,基于干扰区域将边缘用户分簇并分配频段,每个簇内的小基站联合接收簇内用户的发送信号. Hajisami等[13]首次提出了单频段分簇的思想,“单频段”不是为每个簇分配单个频段的意思,而是相邻的簇采用的频段不同,这样就能避免簇间干扰,然而该文献给出了用户的动态归簇方法,并没有给出初始的单频段分簇方法,并且该方案假设网络是六边形的,与实际网络不符.
针对Hajisami等[13]的不足,提出了上行链路中基于JR-CoMP的分簇和资源分配方案.首先,根据用户间的干扰拓扑图将用户和基站分簇,得到多个用户簇及其服务基站簇.然后,对用户簇进行多重子频段分配,在消减簇间干扰的同时为每个簇分配单个或多个子频段.最后,以最大化系统总传输速率为目标,为用户进行功率分配.仿真结果显示,本文方案的频谱效率显著高于相同场景中的已有方案.
1 系统模型假设UDN中包含M个小基站和U个用户,每个小基站为若干个用户服务,每个小基站及其服务的用户组成一个小小区.每个小基站配置Nt根天线,每个用户配置1根天线.小基站随机分布在网络内,用户随机分布在小基站覆盖范围内.子频段集合表示为B={B(1), B(2), …, B(C)},C为子频段的总数量.
将用户分为P个用户簇,分簇后并不改变用户的服务基站.每个用户簇内所有用户的服务基站组成一个服务基站簇,因此基站簇共有P个.每个用户只能在一个用户簇中,而每个基站可以处于多个基站簇中.第p个用户簇内用户的集合表示为Up={1, …, up},第p个基站簇内小基站的集合表示为Mp={1, …, mp},其中,up≤Ntmp,
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{y}}_p^c = \sum\limits_{l \in {U_p}} {s_p^c{\mathit{\boldsymbol{h}}_{pl,p}}\sqrt {a_{pl}^c} {x_{pl}} + \sum\limits_{\begin{array}{*{20}{c}} {q = 1}\\ {q \ne p} \end{array}}^p {\sum\limits_{l \in {U_q}} {s_q^c{\mathit{\boldsymbol{h}}_{ql,p}}\sqrt {a_{ql}^c} } } } {x_{ql}} + {\mathit{\boldsymbol{n}}_p} = }\\ {s_p^c{\mathit{\boldsymbol{H}}_{p,p}}{\mathit{\boldsymbol{x}}_p} + \sum\limits_{q \ne p} {s_q^c{\mathit{\boldsymbol{H}}_{q,p}}{\mathit{\boldsymbol{x}}_q} + {\mathit{\boldsymbol{n}}_p}} } \end{array} $ | (1) |
其中:ypc和np的阶数均为Ntmp×1,np为均值为0,方差为σ2的高斯白噪声向量,其协方差矩阵满足E(npnpH)=σ2INtMp,INtmp为Ntmp阶的单位矩阵,xpl为Up中的第l个用户的发送信号,aplc为Up中的第l个用户在第c个子频段上的发送功率,p=1, 2, …, P,l=1, 2, …, up,hql, p为Uq中的第l个用户到Mp中所有小基站的信道矩阵,阶数为Ntmp×1,Hp, p=[hp1, p, hp2, p, …, hpup, p]为Up中的所有用户到Mp中所有小基站的信道矩阵,
式(1)中等式右边的第1项是期望接收信号,即Up中的用户发送给Mp中小基站的信号,这up个信号相互干扰,是簇内干扰.式(1)中等式右边的第2项是除Up外其他用户簇中的用户发送的信号,是簇间干扰.
Mp中小基站是Up中的用户的服务基站,因此,这些小基站已知Up中的用户到自身的信道矩阵,即已知Hp, p.由于Mp中小基站不是Up之外用户的服务基站,Mp中小基站不知道Hq, p,q≠p.因此,Mp中小基站能采用迫零算法消除簇内干扰,而无法消除簇间干扰.
迫零算法通过处理接收信号来消除期望接收信号间的干扰.用Gpc表示迫零算法的处理矩阵,根据Hajisami等[12]可得,Gpc的表达形式为
| $ \mathit{\boldsymbol{G}}_p^c={\left( {\mathit{\boldsymbol{H}}_{p,p}^{\rm{H}}{\mathit{\boldsymbol{H}}_{p,p}}} \right)^{ - 1}}{\left( {{\mathit{\boldsymbol{H}}_{p,p}}} \right)^{\rm{H}}} $ | (2) |
其中:(·)H表示矩阵的共轭转置,(·)-1表示矩阵的逆.
在式(1)两端分别乘以Gpc,可得
| $ \mathit{\boldsymbol{G}}_p^c\mathit{\boldsymbol{y}}_p^c = s_p^c{\mathit{\boldsymbol{x}}_p} + \mathit{\boldsymbol{G}}_p^c\sum\limits_{q \ne p} {s_q^c{\mathit{\boldsymbol{H}}_{q,p}}{\mathit{\boldsymbol{x}}_q} + \mathit{\boldsymbol{G}}_p^c{\mathit{\boldsymbol{n}}_p}} $ | (3) |
其中:等号右边第1项为期望接收信号,第2项为簇间干扰,第3项为加性高斯白噪声.由式(3)可以看出,Mp中小基站间的联合接收能消除簇内干扰.
Up中的第i个用户在子频段B(c)上的信干噪比(SINR, signal to interference plus noise ratio)为
| $ \begin{array}{*{20}{c}} {\alpha _{pi}^c = }\\ {\frac{{a_{pi}^c{{\left| {\mathit{\boldsymbol{G}}_p^c\left( i \right)s_p^c{\mathit{\boldsymbol{h}}_{pi,p}}} \right|}^2}}}{{\sum\limits_{q \ne p} {\sum\limits_{l \in {U_q}} {a_{pl}^c{{\left| {\mathit{\boldsymbol{G}}_p^c\left( i \right)s_q^c{\mathit{\boldsymbol{h}}_{\mathit{ql},p}}} \right|}^2} + {{\left\| {\mathit{\boldsymbol{G}}_p^c\left( i \right)} \right\|}^2}{\sigma ^2}} } }}} \end{array} $ | (4) |
其中Gpc(i)为矩阵Gpc的第i行. Up中的第i个用户在子频段B(c)上的传输速率为
| $ R_{pi}^c = E{\rm{lb}}\left( {1 + \alpha _{pi}^c} \right) $ | (5) |
其中:E为子频段的带宽.考虑到所有簇中的所有用户,该网络的总传输速率为
| $ \sum\limits_{p = 1}^P {\sum\limits_{i = 1}^{{u_p}} {\sum\limits_{c = 1}^C {R_{pi}^c = } } } \sum\limits_{p = 1}^P {\sum\limits_{i = 1}^{{u_p}} {\sum\limits_{c = 1}^C {E{\rm{lb}}\left( {1 + \alpha _{pi}^c} \right)} } } $ | (6) |
总传输速率与分簇、子频段分配和功率分配有关.笔者研究的目标是:在一定的约束条件下,合理地分簇并分配资源,以最大化系统总传输速率,用公式表达为
| $ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} \mathop {\max }\limits_{{u_p},s_p^c,a_{pi}^c} \end{array}\sum\limits_{p = 1}^P {\sum\limits_{i = 1}^{{u_p}} {\sum\limits_{c = 1}^C {R_{pi}^c} } } }\\ {{\rm{s}}{\rm{.t}}{\rm{.C1:}}\sum\limits_{p = 1}^P {\sum\limits_{i = 1}^{{u_p}} {a_{pi}^c \le {P_{\max }}} } }\\ {{\rm{C}}2;\sum\limits_{c = 1}^C {R_{pi}^c \ge {R_{\min }},\;\;\;\forall p} }\\ {{\rm{C}}3:{U_p} \cap {U_q} = \phi ,\;\;\;\mathit{p} \ne \mathit{q}}\\ {{\rm{C}}4:\sum\limits_{c = 1}^C {s_p^c} \ge 1,\;\;\;\forall p}\\ {{\rm{C5:}}\mathit{a}_{pi}^c > 0,\;\;\;\forall p} \end{array} $ | (7) |
其中:C1表示网络中所有用户的总传输功率不能超过Pmax;C2表示每个用户的传输速率不能低于Rmin;C3表示用户簇中的用户互不重叠;C4表示至少为每个用户簇分配了一个子频段;C5表示每个用户的发送功率大于零.
式(7)的最优解需要遍历所有可能的分簇及所有可能的子频段分配和功率分配,复杂度极高.本文方案给出了一种复杂度相对较低的次优解,将分簇和资源分配分3个步骤进行,分别为分簇、子频段分配和功率分配.第2节给出了分簇方法,将用户和基站分簇;第3节先给出了子频段分配方法,为每个用户簇分配一个或多个子频段,然后推导了在特定分簇和子频段分配下的功率分配.
2 分簇方法本节给出了单频段分簇方法,根据干扰将用户分为多个用户簇,每个用户簇都有一个服务基站簇.用户簇之间互不重叠,而服务基站簇之间可以重叠.
2个小基站距离较近或干扰较大时,若将这2个小基站放在同一个基站簇中,并且将2个小基站服务的所有用户放在同一个用户簇中,则一个小基站的部分边缘用户可能到另一个小基站的位置较远,不适合采用联合接收.因此分簇时,不能将单个小基站服务的所有用户放在同一个用户簇中. Hajisami等[12]中的例子表明,将单个小基站服务的多个边缘用户分别放在不同的簇中,并且为这些簇分配正交的子频段能消减簇间干扰,因此,笔者所提单频段分簇的原则之一是:将同一小小区的多个边缘用户放在不同的用户簇中.
若2个相邻小小区的边缘用户的距离较近,则这2个小小区的小基站能联合接收这2个用户的信号,因此,笔者提出单频段分簇的另一个原则是:将位于相邻小小区并且距离较近的边缘用户放在同一个用户簇中.
基于这2个原则分簇后,可能有一些未被归到任何簇的用户.对于每个这样的用户,计算该用户到每个基站簇的平均干扰强度,选出干扰最大的基站簇,将该用户归到该基站簇对应的用户簇中.
假设用户x和用户y处于2个不同的小小区中,定义一个直观的值γx, y来表示这2个用户之间的干扰强度:
| $ {\gamma _{x,y}} = {\gamma _{\mathit{y},\mathit{x}}} = \max \{ {\mathit{\Omega }_{x,{v_y}}}\mathit{,}{\mathit{\Omega }_{\mathit{y},{v_x}}}\} $ | (8) |
其中:Ωx, vy为用户x到用户y服务基站之间的路径损耗.若用户x和用户y是相邻小小区的边缘用户并且两者距离较近,则两者之间干扰较大,γx, y相对较小.若用户x和用户y中至少有一个是中心用户,则γx, y相对较大. γx, y越小,用户x和用户y之间的干扰强度越大.
定义干扰门限D,若γx, y小于等于D,则认为用户x和用户y之间存在干扰,否则认为用户x和用户y之间不存在干扰.根据用户间的干扰强度构建用户干扰拓扑图,图中的节点表示用户,边表示位于不同小小区的2个用户间的干扰.若γx, y小于等于D,则两用户对应的节点之间有条边,边的长度为γx, y.若γx, y大于D,则两用户对应的节点之间无边.同一小小区内的多个用户之间无边.通过合理地设置D,使得位于相邻小小区的干扰较大的边缘用户之间有条边,而任何小小区的中心用户与其他用户之间无边.
用G表示用户干扰拓扑图.基于G进行分簇,具体的分簇方法描述如下:
初始化:令p=1,创建空集Up和空集Mp.
while G中边的数量大于0
从图中找到最短的边;
if最短的边有多条
随机选取其中一条边;
end if
将这条边的2个节点所对应的用户放在用户簇Up内;
将Up中所有用户的服务基站放在基站簇Mp内;
在用户干扰拓扑图中删除Up中用户对应的节点及与这些节点相连的边,得到新的用户干扰拓扑图,赋值给G.
p=p+1;
创建空集Up和空集Mp;
end while
P=p-1;
while G中有度为零的节点
从图中随意找一节点z;
for p=1:P
令γ=0且θz, p=0;
计算节点z与
θz, p=γ/|Up|;
end for
θz, e=min{θz, 1, θz, 2, …, θz, P},将节点z对应的用户归到用户簇Ue中,将节点z对应的用户的服务基站放在基站簇Me内;
删除节点z,得到新的用户干扰拓扑图,赋值给G;
end while
上述方法中,|·|表示集合的势.单频段分簇方法依次选出干扰较大的边缘用户,将这些用户放在新的用户簇中,然后再根据未归簇的用户与每个基站簇的路径损耗将该用户归簇.分簇后,同一个小小区的多个边缘用户分别在不同的用户簇中.
3 资源分配 3.1 多重子频段分配本节给出了多重子频段分配方法,为每个用户簇分配单个或多个子频段,每个用户簇内的所有用户共享分得的子频段.
如前所述,同一个小小区的多个边缘用户分别在不同的用户簇中,如果为这些用户簇分配相同的子频段,则簇间干扰严重.因此,分配子频段的原则是:为包含同一个小小区用户的多个簇分配不同的子频段.基于该原则,为每个用户簇分配单个子频段后,若还有剩余的子频段,则基于以上原则再次为每个用户簇分配子频段,直至没有子频段可分配给任何用户簇.
结合以上分析,提出的子频段分配方法描述如下:
初始化:用SBp表示分配给第p个用户簇的子频段的集合,令SBp为空集,index=0.
while index < P
index=0;
for n=1:P
找出基站簇Mn内小基站覆盖范围内已经分配过子频段的用户,用Bn表示这些用户分配到的子频段组成的集合;
if
从CBBn中任选一子频段加入到集合SBn内;
else
index=index+1;
end if
end for
if index==P
break;
end if
end while
CBBn表示Bn在B中的补集.在每次while循环时,首先令index=0,然后遍历每个用户簇,寻找可以分配给用户簇的子频段,如果某个用户簇没有可用的子频段,则令index=index+1.在while循环内遍历用户簇后,若index==P,则该次while循环中没有为任何用户簇分配子频段,跳出while循环,子频段分配结束.
在簇较少且子频段较多的情况下,若为每个簇分配单个子频段,则频段的利用率不高.多重子频段分配在保证消减簇间干扰的同时,尽可能地为每个簇多分配子频段,提高频段利用率.
3.2 功率分配对网络进行分簇和子频段分配之后,式(7)可以简化为式(9),约束条件为C1~C3.
| $ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} \mathop {\max }\limits_{a_{pi}^c} \end{array}\sum\limits_{p = 1}^P {\sum\limits_{i = 1}^{{u_p}} {\sum\limits_{c = 1}^C {R_{pi}^c} } } }\\ {{\rm{s}}{\rm{.t}}{\rm{.C1:}}\sum\limits_{p = 1}^P {\sum\limits_{l = 1}^{{u_p}} {a_{pi}^c \le {P_{\max }}} } }\\ {{\rm{C}}2;\sum\limits_{c = 1}^C {R_{pi}^c \ge {R_{\min }}} }\\ {{\rm{C3:}}\mathit{a}_{pi}^c \ge 0} \end{array} $ | (9) |
式(9)可以用拉格朗日对偶分解法来进行求解,并且该方法的计算复杂度较低.用β、ε和ω表示拉格朗日乘子,构建拉格朗日函数,表示为
| $ \begin{array}{*{20}{c}} {L\left( {a_{pi}^c,\beta ,\varepsilon ,\omega } \right) = \sum\limits_{p = 1}^P {\sum\limits_{i = 1}^{{u_p}} {\sum\limits_{c = 1}^C {E{\rm{lb}}\left( {1 + } \right.} } } }\\ {\left. {\frac{{a_{pi}^c{{\left| {\mathit{\boldsymbol{G}}_p^c\left( i \right)s_p^c{\mathit{\boldsymbol{h}}_{pi,p}}} \right|}^2}}}{{\sum\limits_{q \ne p} {\sum\limits_{l \in {U_q}} {a_{pl}^c{{\left| {\mathit{\boldsymbol{G}}_p^c\left( i \right)s_q^c{\mathit{\boldsymbol{h}}_{\mathit{ql},p}}} \right|}^2} + {{\left\| {\mathit{\boldsymbol{G}}_p^c\left( i \right)} \right\|}^2}{\sigma ^2}} } }}} \right) - }\\ {\beta \left( {\sum\limits_{p = 1}^P {\sum\limits_{l = 1}^{{u_p}} {a_{pi}^c - {P_{\max }}} } } \right) - \varepsilon \left( {{\mathit{R}_{\min }} - \sum\limits_{c = 1}^C {R_{pi}^c} } \right) + \omega a_{pi}^c} \end{array} $ | (10) |
如果式(9)中的约束条件得到满足,根据凸优化理论可知,一定存在最优解.根据KKT(Karush-Kuhn-Tucker)定理,式(9)的最优解可以由式(11)求得:
| $ \frac{{\partial \mathit{L}\left( {a_{pi}^c,\beta ,\varepsilon ,\omega } \right)}}{{\partial a_{pi}^c}} = 0 $ | (11) |
| $ \begin{array}{*{20}{c}} {a_{pi}^c = \left[ {\frac{{E\left( {1 + \varepsilon } \right)}}{{\ln 2\left( {\rho - \omega } \right)}} - } \right.}\\ {{{\left. {\frac{{\sum\limits_{q \ne p} {\sum\limits_{l \in {U_q}} {a_{pl}^c{{\left| {\mathit{\boldsymbol{G}}_p^c\left( i \right){\mathit{\boldsymbol{h}}_{\mathit{ql},p}}} \right|}^2} + {{\left\| {\mathit{\boldsymbol{G}}_p^c\left( i \right)} \right\|}^2}{\sigma ^2}} } }}{{{{\left| {\mathit{\boldsymbol{G}}_p^c\left( i \right){\mathit{\boldsymbol{h}}_{pi,p}}} \right|}^2}}}} \right]}^ + }} \end{array} $ | (12) |
用次梯度下降法计算乘子β、ε和ω,使得运用一个固定的步长可以将凸优化问题的最优解收敛到一个很小的范围内.根据次梯度下降法可得
| $ {\beta ^{\left( {j + 1} \right)}} = {\left[ {{\beta ^{\left( j \right)}} - \mathit{\Lambda }_1^{\left( j \right)}\left( {{P_{\max }} - \sum\limits_{p = 1}^P {\sum\limits_{l = 1}^{{u_p}} {a_{pi}^c} } } \right)} \right]^ + } $ | (13) |
| $ {\varepsilon ^{\left( {j + 1} \right)}} = {\left[ {{\varepsilon ^{\left( j \right)}} - \mathit{\Lambda }_2^{\left( j \right)}\left( {\sum\limits_{c = 1}^C {R_{pi}^c - {R_{\min }}} } \right)} \right]^ + } $ | (14) |
| $ {\omega ^{\left( {j + 1} \right)}} = {\left[ {{\omega ^{\left( j \right)}} - \mathit{\Lambda }_3^{\left( j \right)}a_{pi}^c} \right]^ + } $ | (15) |
其中:Λ1(j)、Λ2(j)和Λ3(j)为迭代步长,j为迭代次数,[k]+=max(0, k).
4 性能比较及仿真本节仿真了本文方法的性能,并与CoMP全频段分簇方案和Hajisami等[13]中的DJP-LM方案进行对比.为了公平对比,还仿真了本文方案中考虑分簇与子频带分配但是没有功率分配算法的性能,在仿真图中用“所提NPA方案”表示.
4.1 仿真参数仿真场景如下:20个小基站随机分布在500 m×500 m的范围内,小基站覆盖半径为25 m,每个小基站覆盖范围内随机分布50个用户,共50个子频段,路径损耗模型为38.88+32lg(d0)+10λlg(d),d为传输距离,d0为已知的参考距离,假设CoMP全频段分簇方案和DJP-LM方案中每个簇包含2~4个小基站.其他仿真参数如表 1所示,λ为路径损耗指数.
|
|
表 1 仿真参数 |
仿真中采用如下信号传播模型:
| $ {P_{{\rm{rx}}}} = {K_0}{\left( {\frac{\mathit{d}}{{{d_0}}}} \right)^{ - \lambda }}\mathit{\psi }{\mathit{P}_{{\rm{tx}}}} $ | (16) |
其中:Prx为接收信号功率,Ptx为发送信号功率,随机变量ψ表示阴影效应造成的慢衰落并服从对数正态分布,K0为常数,表示距离为d0时的路径损耗.
4.2 仿真结果图 1所示为4种方案的中断概率对比.中断概率定义为:用户的α低于门限值μ的概率,即P(α < μ)=1-P(α>μ).从图 1能看出,对于4种方案,λ=3时的中断概率低于λ=2.5时的中断概率.这是因为在其他参数相同的情况下,λ越高,路径损耗越大,簇间干扰越小,从而其中断概率越低.从图 1还能看出,本文方案的中断概率低于所提NPA方案,所提NPA方案的中断概率低于DJP-LM方案,DJP-LM方案的中断概率低于CoMP全频段分簇方案.当μ为10dB且λ=3时,本文方案的中断概率为0.07,所提NPA方案的中断概率为0.08,DJP-LM方案和CoMP全频段分簇方案的中断概率分别为0.19和0.30. CoMP全频段分簇方案中,所有的簇使用相同的频段,簇内的边缘用户会对相邻的簇造成簇间干扰,而DJP-LM方案本质上是单频段分簇,相邻的簇采用不同的子频段,有效消减了簇间干扰,因此DJP-LM方案的中断概率低于CoMP全频段分簇方案. DJP-LM方案为每个簇分配单个子频段,而所提NPA方案为每个簇分配单个或多个子频段,频段利用率高,因此所提NPA方案的中断概率显著低于DJP-LM方案.与所提NPA方案相比,本文方案以最大化总吞吐量为目标为每个用户分配功率,而SINR是决定吞吐量的关键因素,因此,本文方案的中断概率低于所提NPA方案.
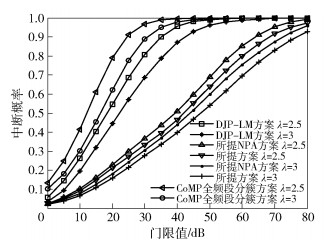
|
图 1 不同门限值的中断概率 |
图 2对比了3种方案在不同信噪比和不同路径损耗指数下的用户平均频谱效率.信噪比较低时,3种方案的用户平均频谱效率比较接近.随着信噪比的增加,所提NPA方案的频谱效率显著高于CoMP全频段分簇方案和DJP-LM方案.当信噪比为30 dB且λ=3时,所提NPA方案的用户平均频谱效率为8.65 bit·s-1·Hz-1,DJP-LM方案和CoMP全频段分簇方案的用户平均频谱效率分别为6.78 bit·s-1·Hz-1和4.98 bit·s-1·Hz-1.原因在于:与CoMP全频段分簇方案相比,所提NPA方案能消减簇间干扰,与DJP-LM方案相比,所提NPA方案为每个簇分配单个或多个子频段,增加了用户的平均带宽.从图 2还能看出,对于每种方案,λ越高,平均频谱效率越高,这是因为增大λ能减少簇间干扰.

|
图 2 不同信噪比时的用户平均频谱效率 |
图 3比较了λ=3时4种方案在不同用户数量下的小小区平均频谱效率.从图中能看出,随着用户数量的增加,小小区平均频谱效率也随之增加,并且本文方案和所提NPA方案的平均频谱效率显著高于其他2种方案.当用户数量为50个时,本文方案和所提NPA方案的小小区平均频谱效率分别为790.29 bit·s-1·Hz-1和700.89 bit·s-1·Hz-1,DJP-LM方案和CoMP全子频段分簇方案的小小区平均频谱效率分别为347.85 bit·s-1·Hz-1和273.26 bit·s-1·Hz-1.
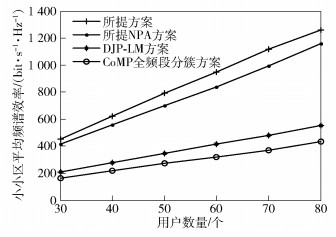
|
图 3 不同用户数量时的小小区平均频谱效率 |
提出的上行链路中基于JR-CoMP的分簇和资源分配方案,首先基于用户间的干扰拓扑图对用户进行单频段分簇,然后为每个用户簇分配子频段,并为每个用户分配功率.与已有的单频段分簇及资源分配相比,所提出的多重子频段分配根据子频段数量及用户簇间的干扰,为每个用户簇分配单个或多个子频段,提高了频段利用率,增大了用户的平均带宽,从而提高了系统频谱效率和吞吐量.然而,本文模型没有涉及宏小区与小小区间的层间干扰,UDN中层间干扰下的资源分配有待于进一步研究.
| [1] |
Ge Xiaohu, Tu Song, Mao Guoqiang, et al. 5G ultra-dense cellular networks[J]. IEEE Wireless Communications, 2016, 23(1): 72-79. DOI:10.1109/MWC.2016.7422408 |
| [2] |
王莹, 缪中宇, 张平. 超高密度网络关键技术及研究现状[J]. 北京邮电大学学报, 2015, 38(5): 1-17. Wang Ying, Miao Zhongyu, Zhang Ping. Research progress and key technologies in ultra dense networks[J]. Journal of Beijing University of Posts and Telecommunications, 2015, 38(5): 1-17. |
| [3] |
蔡振浩, 赵昆, 陈文. TD-LTE-A系统下行多用户CoMP联合预编码算法[J]. 北京邮电大学学报, 2015, 38(1): 67-70. Cai Zhenhao, Zhao Kun, Chen Wen. Research on CoMP joint transmission for downlink MU-MIMO in TD-LTE-A[J]. Journal of Beijing University of Posts and Telecommunications, 2015, 38(1): 67-70. |
| [4] |
Miyamoto K, Kuwano S, Terada J, et al.Uplink joint reception with LLR forwarding for optical transmission bandwidth reduction in mobile fronthaul[C]//2015 IEEE 81st Vehicular Technology Conference.New York: IEEE Press, 2015: 1-5.
|
| [5] |
Rakhmania A E, Tsai P Y, Setyawati O.Combined per-user SLNR and SINR criterions for interference alignment in uplink coordinated multi-point joint reception[C]//Signal and Information Processing Association Summit and Conference.New York: IEEE Press, 2015: 1-5.
|
| [6] |
Chih-Lin I, Huang Jinri, Duan Ran, et al. Recent progress on C-RAN centralization and cloudification[J]. IEEE Access, 2014(2): 1030-1039. |
| [7] |
Shang Peng, Zhang Lu, You Mingli, et al.Performance of uplink joint reception CoMP with antenna selection for reducing complexity in LTE-A systems[C]//2015 IEEE Wireless Communications and Networking Conference.New York: IEEE Press, 2015: 977-982.
|
| [8] |
Li Yong, Huang Zhangqin.Performance of LTE-A uplink with joint reception and inter-cell interference coordination[C]//2013 IEEE 11th International Conference on Dependable, Autonomic and Secure Computing.New York: IEEE Press, 2013: 492-496.
|
| [9] |
Ha V N, Le L B, Dào N D. Coordinated multipoint transmission design for cloud-RANs with limited fronthaul capacity constraints[J]. IEEE Transactions on Vehicular Technology, 2016, 65(9): 7432-7447. DOI:10.1109/TVT.2015.2485668 |
| [10] |
Bassoy S, Farooq H, Imran M A, et al. Coordinated multi-point clustering schemes:a survey[J]. IEEE Communications Surveys & Tutorials, 2017, 19(2): 743-764. |
| [11] |
Feng Si, Feng Wei, Mao Hongliang, et al.Overlapped clustering for CoMP transmissions in massively dense wireless networks[C]//2014 IEEE International Conference on Communication Systems.New York: IEEE Press, 2014: 308-312.
|
| [12] |
Hajisami A, Pompili D. Joint virtual edge-clustering and spectrum allocation scheme for uplink interference mitigation in C-RAN[J]. Ad Hoc Networks, 2018(72): 91-104. |
| [13] |
Hajisami A, Pompili D. Dynamic joint processing:achieving high spectral efficiency in uplink 5G cellular networks[J]. Computer Networks, 2017, 126: 44-56. DOI:10.1016/j.comnet.2017.06.026 |



