2. 广西密码学与信息安全重点实验室, 桂林 541000;
3. 中国石油大学(华东) 信息与控制工程学院, 青岛 266580
针对端信息跳变主动防御技术中跳变策略单一的问题,将多样异构的跳变模式引入端信息跳变系统,拓展了端信息的定义,并给出跳变策略的自适应调整方案.提出一种基于深度信念网络的端信息跳变自适应模型,形式化地描述了模型中数据收集、特征提取和状态预测等过程,定义了端信息跳变网络状态特征指标,并建立了特征数据集.利用深度信念网络对数据集进行建模,利用马尔可夫链预测下一周期的网络状态,并根据预测结果选取异构的跳变模式,从而实现端信息跳变模式的自适应变化.实验结果显示,模型网络状态识别和预测具有较高的准确性,并且异构的跳变策略能够有效抵御不同的攻击类型,进而验证了端信息跳变自适应模型的有效性和安全性.
2. Guangxi Key Laboratory of Cryptography and Information Security, Guangxi 53000, China;
3. College of Information and Control Engineering, China University of Petroleum(East China), Qingdao 266580, China
For problem of single hopping strategy in active cyber defense of end hopping, the multiple and heterogeneous hopping patterns are introduced into the end hopping system, the definition of end information is expanded, and the self-adaptive adjustment scheme of the end hopping is given. Further, an adaptive model of end hopping based on deep belief network is proposed, and the process of data collection, feature extraction and state prediction are formalized. The state feature index of end hopping network is defined and the characteristic data set is established. The Markov chain is used to predict the state of network in the next cycle. The heterogeneous hopping mode is selected according to the prediction results. Thus, the adaptive change of the end hopping mode is realized. Experiments show that the network state recognition and prediction of the model all have high accuracy, and the heterogeneous hopping strategy can effectively resist different types of attacks, which illustrates the validity and security of the end hopping adaptive model.
近年来网络安全问题引起人们高度关注.防火墙、入侵检测系统等传统的网络防御手段本质上是一种敌暗我明的被动防御,对于网络防御十分不利.主动网络防御手段应运而生并成为研究热点.
主动网络防御是一种前摄性的防御技术,其主要思想是在攻击者发起攻击之前进行动态防御部署,从而扭转防御者在网络对抗中的不利地位.端信息跳变技术就是一种主动网络防御手段,它借鉴军事跳频通信思想而提出,通过将通信双方按照一定的跳变方案,伪随机地改变某一方或双方的端口、地址、时隙、加密方法甚至协议等端信息,从而迷惑和干扰攻击者,实现主动网络防御[1].然而,随着网络环境日益复杂,单一固定的跳变模式难以有效应对错综复杂的网络攻击.如何根据不同的网络环境自适应地选取不同的跳变策略,从而实现跳变策略的多样异构成为端信息跳变主动网络防护应用的一个关键问题.
笔者针对端信息跳变中跳变策略单一的问题开展研究,拓展端信息的定义并提出了基于深度信念网络的端信息跳变自适应模型,通过多端的数据收集系统收集端信息跳变网络下的原始数据,对跳变网络环境的特点进行分析并定义跳变网络的特征指标,从而建立网络的特征数据集,在对数据集进行标注后利用深度信念网络对数据集进行自主学习得到当前网络状态,采用马尔可夫链(MC,Markov chain)预测方法对未来的网络状态做出预测,然后跳变系统根据预测结果选取异构的跳变策略加以应对.
1 相关工作主动网络防御领域近年来开展的相关研究工作主要包括移动目标防御技术、拟态安全防御技术以及端信息跳变技术.
移动目标防御技术[2](MTD,moving target defense)由美国国家科学技术委员会于2011年提出,其主要思想是使构建、分析、评价、部署策略多样化和伪随机化,从而增加攻击的成本以及复杂度,降低攻击成功的概率.在对移动目标防御的研究中,Venkatesan[3]提出了一种移动目标防御模型来缓解DDoS攻击,从理论上和仿真两方面验证了该方法的可行性. Wang[4]通过软件定义网络扩大了地址动态变化的范围,从而实现了移动目标防御在网络层上的应用.
拟态安全防御(MSD,mimic security defense)则由邬江兴院士于2014年提出,它是指除目标对象的服务功能和性能之外,系统的硬件、软件等均可以通过动态变化的方式进行拟态伪装,达到保护系统免于攻击的主动网络防御目的[5].在拟态安全防御的研究方面,Hu[6]等提出了一种新颖的拟态防御框架,并通过理论分析和仿真实验验证了其安全性;仝青[7]设计了一种基于拟态防御的Web服务器;王禛鹏[8]设计了一种基于拟态安全防御的DNS框架,并实验验证了其安全性和有效性.
对于移动目标防御技术、拟态安全防御技术和端信息跳变技术而言,能否有效通过当前网络状态自适应地选取多样异构的跳变策略是一个关键问题.雷程[9]等提出了一种基于网络攻击面自适应转换的移动目标防御技术,增大了网络防御收益并增强了跳变防御的不可预测性. Ma[10]等提出了一种基于可满足性模理论的自适应跳变方法,降低跳变实施的性能开销.最相近的研究是赵春蕾[11]和刘江[12]的工作.赵春蕾[11]对端信息跳变自适应的问题进行了研究,分别从时间维度、空间维度提出了时间自适应策略和空间自适应策略,并给出时空混合自适应策略,增强了抗攻击性,但基于规则判别型的网络状态评估手段容易造成误判且对新型的网络攻击手段无法准确识别.刘江[12]则基于非广延熵和Sibson熵融合的实时网络异常度量算法并设计了跳变空间自调整策略,提高防御收益,但该模型是基于流量分析的模型,存在对于不依赖流量的攻击类型难以识别的问题,另外,该模型并不能更近一步地对跟随攻击还是盲目攻击进行判断,从而使得防御措施缺乏针对性.目前的相关研究没有对端信息跳变网络状态检测方法的准确性和有效性开展研究和探讨,并且自适应跳变策略选取过于单一.
2 自适应端信息跳变模型 2.1 深度信念网络模型结构深度信念网络(DBN,deep belief network)是由Hinton等于2006年提出[13],它由多层的限制玻尔兹曼机(RBM,restricted boltzmann machine)无监督算法堆叠训练而成,并在最后一层添加有监督的反向迭代(BP,back propagation)层从而达到整体微调的作用[14].
相较于传统的BP神经网络而言,深度信念网络拥有RBM的无监督训练过程,在尽可能地保留原始特征特点的同时降低特征的维度,使得DBN尽可能避免了BP神经网络算法的需要大量的标注训练数据,收敛缓慢和容易收敛到局部最优点等缺点[15]. RBM作为组成深度置信网络的基础部件,是一种基于能量的模型. RBM的能量函数可定义为
| $ E\left( {\mathit{\boldsymbol{v}}{\bf{,}}\mathit{\boldsymbol{h}}{\bf{;}}\mathit{\boldsymbol{\theta }}} \right) = - \sum\limits_{ij} {{W_{ij}}{v_i}{h_j} - \sum\limits_i {{b_i}{v_i} - \sum\limits_j {{a_j}{h_j}} } } $ | (1) |
其中:θ为RBM的参数矩阵{W, a, b},w表示连接隐藏和可见单元的权重,a、b分别表示可见和隐藏层的偏置矩阵.有了v和h的联合配置的能量之后,就可以得到v和h的联合概率.
| $ {P_\theta }\left( {\mathit{\boldsymbol{v,h}}} \right) = \frac{1}{{Z\left( \mathit{\boldsymbol{\theta }} \right)}}\exp \left( { - E\left( {\mathit{\boldsymbol{v}}{\bf{,}}\mathit{\boldsymbol{h}}{\bf{;}}\mathit{\boldsymbol{\theta }}} \right)} \right) $ | (2) |
其中:Z(θ)是归一化因子,也称为配分函数,根据式(1),可以将式(2)写成
| $ \begin{array}{*{20}{c}} {{P_\theta }\left( {\mathit{\boldsymbol{v,h}}} \right) = \frac{1}{{Z\left( \mathit{\boldsymbol{\theta }} \right)}}\exp \left( {\sum\limits_{i = 1}^D {\sum\limits_{j = 1}^F {{\mathit{W}_{ij}}{v_i}{h_j}} } + } \right.}\\ {\left. {\sum\limits_{i = 1}^D {{v_i}{b_i}} + \sum\limits_{j = 1}^F {{h_j}{a_j}} } \right)} \end{array} $ | (3) |
由式(3)可求得P(v, h)对h的边缘分布:
| $ {P_\theta }\left( \mathit{\boldsymbol{v}} \right) = \frac{1}{{Z\left( \mathit{\boldsymbol{\theta }} \right)}}\sum\limits_h {\exp \left[ {{\mathit{\boldsymbol{v}}^{\rm{T}}}\mathit{\boldsymbol{Wh}} + {\mathit{\boldsymbol{a}}^{\rm{T}}}\mathit{\boldsymbol{h}} + {\mathit{\boldsymbol{b}}^{\rm{T}}}\mathit{\boldsymbol{v}}} \right]} $ | (4) |
通过最大化似然函数P(v)得到RBM的学习目标,最大化P(v)等同于最大化log(P(v))=L(θ):
| $ L\left( \mathit{\boldsymbol{\theta }} \right) = \frac{1}{N}\sum\limits_{n = 1}^N {\log {P_{_\theta }}} \left( {{v^{\left( n \right)}}} \right) $ | (5) |
RBM的学习方法采用对比散列法,即根据可见层数据得到隐藏层的状态,然后通过隐藏层的状态重构可见层状态,从而更新权重.
笔者提出的DBN网络结构在多层RBM基础上添加了一层Softmax多分类层来实现有监督的BP的微调. Softmax的函数可以表示为
| $ P\left( i \right) = \frac{{\exp \left( {\mathit{\boldsymbol{\theta }}_i^{\rm{T}}x} \right)}}{{\sum\limits_{k = 1}^K {\exp \left( {\mathit{\boldsymbol{\theta }}_k^{\rm{T}}x} \right)} }} $ | (6) |
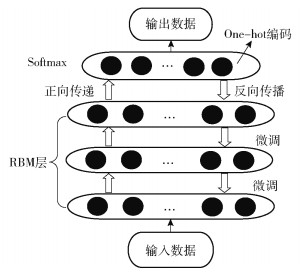
其中θkTx为RBM训练结果的多个输入.笔者采用One-hot编码的方式作为标签来标注不同的安全等级. DBN模型结构如图 1所示.该DBN模型的训练过程分为2步:第1步,单独无监督地训练每一层RBM网络,确保特征向量映射到不同特征空间时,都尽可能多地保留特征信息;第2步,在最后的Softmax层进行BP的有监督训练,将误差信息自顶向下到每一个RBM层进行微调.
|
图 1 深度信念网络模型结构 |
传统端信息包括IP、端口、协议等组成,假设为endInfom=(IPm, Portm, Protocalm, …).将跳变策略加入端信息的定义中,即将端信息的定义在原有基础上扩展为endInfom=(IPm, Portm, Protocalm, …, Strategym),并给出了跳变策略的自适应跳变方案.在此基础上,提出了基于深度信念网络的端信息跳变系统自适应模型.
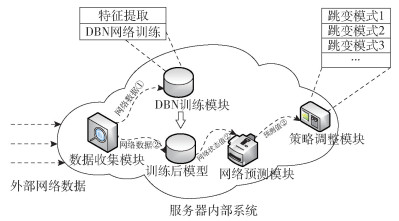
基于深度信念网络的自适应端信息跳变模型主要包含协同工作的4个模块,分别是数据收集模块、DBN训练模块、状态预测模块和策略调整模块,如图 2所示.模型在时序上可以分为训练部分(图 2中的①部分)和实时系统部分(图 2中的②部分),①部分获取大量的数据进行DBN的模型训练,得到训练后的模型供②部分使用,下面对2个部分和各个功能模块进行描述.
|
图 2 基于深度信念网络的端信息跳变模式自适应模型 |
训练部分首先通过数据收集模块收集每个IP和端口在单位收集周期内接收的不同类型的数据,数据收集的过程可形式化描述为
| $ \begin{array}{*{20}{c}} {\{ {\rm{en}}{{\rm{d}}_1}\left( {{\rm{i}}{{\rm{p}}_1},{\rm{por}}{{\rm{t}}_1}} \right),{\rm{en}}{{\rm{d}}_2}\left( {{\rm{i}}{{\rm{p}}_2},{\rm{por}}{{\rm{t}}_2}} \right), \cdots, {\rm{en}}{{\rm{d}}_i}\left( {{\rm{i}}{{\rm{p}}_i},{\rm{por}}{{\rm{t}}_i}} \right){\rm{\} }} \to }\\ {{{{\mathop{\rm info}\nolimits} }_{ikm}}\left( {0 < \mathit{i < }N,\;0\mathit{ < k < K}{\rm{, }}0\mathit{ < m < M}} \right)} \end{array} $ | (7) |
其中:i表示IP的序号,k表示收集周期序号,m表示数据的类型序号.将得到的原始数据矩阵导入DBN训练模块中进行处理. DBN训练模块对原始数据信息进行特征提取和处理,并对特征数据以收集周期为单位进行人工标签,得到特征数据集:
| $ {\rm{Feature = \{ featur}}{{\rm{e}}_{kq}}\left( {0 < \mathit{k} < \mathit{K},\;0 < \mathit{q} < \mathit{Q}} \right){\rm{,labe}}{{\rm{l}}_k}\} $ | (8) |
其中:q表示特征序号,k表示收集周期序号.
将某一周期内的特征作为输入,这一周期的网络状态标签作为输出,利用DBN进行训练.最后经过DBN模型的训练可以得到每一个神经元之间的权重信息Wij及偏置信息b,这一过程可以形式化描述为
| $ {\rm{f}}\left( {\mathit{info}} \right) \to \mathit{Feature} \to {\rm{\{ }}{{\rm{W}}_{{\rm{ij}}}},\mathit{\boldsymbol{b}}\} $ | (9) |
其中:info为收集的原始数据,f()表示从原始数据到特征数据集的变化函数.通过每一个神经元输入输出的关系
网络预测模块选取连续的多个周期的网络状态值,利用马尔可夫链对下一个周期的网络状态做出评估,从而完成从实时收集的数据到网络状态预测值的映射,预测过程可形式化描述为
| $ \begin{array}{*{20}{c}} {M\{ g\left[ {f\left( {{\rm{info}}{'_i}} \right)} \right],g\left[ {f\left( {{\rm{info}}{'_{i + 1}}} \right)} \right], \cdots ,g\left[ {f\left( {{\rm{info}}{'_j}} \right)} \right]\} \to }\\ {{\rm{statu}}{{\rm{s}}_{j + 1}}\left( {j - i + 1 = d,0 < \mathit{i} < j} \right)} \end{array} $ | (10) |
其中:info′i表示实时收集的某一周期的原始数据信息,g()表示训练后模型输入特征到输出状态的映射关系,M()表示马尔可夫链预测过程,d表示预测时选取的网络状态值个数,statusj+1表示下一周期的网络状态值.针对不同的预测值statusj+1,策略调整模块将选取不同的跳变模式策略加以应对,达到跳变策略自适应跳变的目的.
3 关键问题 3.1 特征提取与指标选定在收集到足量的数据之后,根据端信息跳变的网络环境,提取了七大特征,并建立了端信息跳变网络的特征数据集.首先,假设一个收集周期为T,选取的特征如表 1所示.
|
|
表 1 特征描述表 |
其中,NTCP、NUDP、NICMP的大小反映了当前网络环境“量”的一个特性,即数据流量大小的特性. Alert的多少反映了当前网络环境“质”的特性,即数据流量恶意与否的特性,由snort入侵检测系统收集[16],警报越多,则说明恶意的流量越多,危险也就越大. SNet/ANet、SNet/NNet、SAlert/Alert是用来反映数据量变化的特性,反映端信息跳变网络环境中特殊攻击手段的特有属性.
将针对端信息跳变系统的攻击分为盲目攻击(攻击者随机攻击跳变系统中的端信息)和半盲攻击(攻击者掌握一定规律,攻击端信息集合中的部分子集)和跟随攻击(攻击者掌握跳变规律,跟随跳变端信息实现攻击). SNet/ANet用于反映盲目攻击的风险,盲目攻击的风险越大,其值越小,其中SNet是指T内提供服务端信息的流量,ANet是NTCP、NUDP和NICMP的流量总和;SNet/NNet和SAlert/Alert用于反映半盲攻击或跟随攻击的风险,且它们的值越大,表示半盲攻击或跟随攻击的风险越大,其中NNet是在无攻击的情况下设定的一个提供服务的端信息流量的正常值,SAlert是指T内提供服务的端信息产生的警报个数.
3.2 网络状态预测通过DBN的训练模型只是得出了当前的网络状态,在对网络状态的预测过程中,采取一种基于马尔可夫链的时序预测方法对离散型数据进行预测.马尔可夫链是一种特殊的随机过程,且下一时刻的状态只与当前时刻状态有关,与之前的时刻状态无关.
对于随机变量序列X={X(t), t∈T}, T=0, 1, 2, …, 其状态空间为S = {0, 1, 2, …, }.如果对于任意的正整数m、n、k,以及任意的状态值{xn+k, xn, …,x2, x1}, 有
| $ \begin{array}{*{20}{c}} {P\{ X\left( {n + k} \right) = }\\ {{x_{n + k}}\left| {X\left( n \right) = {x_n}, \cdots ,X\left( 2 \right) = {x_2},\mathit{X}\left( 1 \right){\rm{ = }}{\mathit{x}_1}\} = } \right.}\\ {P\{ X\left( {n + k} \right) = {x_{n + k}}\left| {X\left( n \right) = {x_n}\} } \right.} \end{array} $ |
成立,则称XT为马尔可夫链.其中P{X(n)=xn}表示系统在n时处于状态xn时的概率.若记系统在n时所在的状态为i, 在n+k时所在的状态为j,那么系统从状态i转移到状态j时的条件概率P{X(n+k)=j|X(n)=i}称为马尔可夫链的k步转移概率,记为pij(k)(n).特别地,当k=1时,称之为马尔可夫链的转移概率,通常记为pij.
由转移概率组成的矩阵称为马尔可夫链转移概率矩阵,其形式可描述为
笔者分析了端信息跳变的网络环境特点,并从中提取了七大特征,其中NTCP、NUDP、NICMP的大小反映了当前网络环境的量,Alert报警信息的多少反映了当前网络环境的质,而以上都是普通网络环境下的网络属性.针对端信息跳变网络端信息不断变化的网络特点,又引入了SNet/ANet、SNet/NNet、SAlert/Alert三大特征来表示跳变网络的特有属性.这里将对选取的这3种属性的有效性进行分析.
SNet/ANet用于反映盲目攻击的风险,满足
| $ \frac{{{S_{{\rm{Net}}}}}}{{{A_{{\rm{Net}}}}}} = \frac{{g{D_{{\rm{Net}}}} + e{O_{{\rm{Net}}}}}}{{{D_{{\rm{Net}}}} + {O_{{\rm{Net}}}}}},0 \le e,\mathit{g} \le 1 $ | (11) |
其中:DNet表示盲目攻击流量,ONet表示除攻击之外的正常流量,g表示盲目攻击流量中实际命中端信息流量占总的盲目攻击流量的比值,e表示正常流量中实际提供服务端信息的流量占总正常流量的比值.将式(10)中的DNet作为参数,ONet作为常数进行求导可得
| $ f'\left( {{D_{{\rm{Net}}}}} \right) = \left( {\frac{{{S_{{\rm{Net}}}}}}{{{A_{{\rm{Net}}}}}}} \right)' = \frac{{\left( {g - e} \right){O_{{\rm{Net}}}}}}{{{{\left( {{D_{{\rm{Net}}}} + {O_{{\rm{Net}}}}} \right)}^2}}} $ | (12) |
其中:在盲目攻击的情况下,g的值是极小的,同时正常流量中提供服务的端信息所产生的流量应该是占大部分的,故e的值在盲目攻击情况下应是大于g的,有0 < g < e < 1,所以
| $ \frac{{{S_{{\rm{Net}}}}}}{{{N_{{\rm{Net}}}}}} = \frac{{g{D_{{\rm{Net}}}} + {O_{{\rm{Net}}}}}}{{{N_{{\rm{Net}}}}}} $ | (13) |
其中:SNet/NNet是一个随攻击流量DNet增大而增长的特征值,并且由于此时的攻击流量命中端信息的概率增大,从而g值是一个接近1的值,所以该特征值在攻击流量增长的情况下会有很明显的变化.
对于特征SAlert/Alert而言,它可以用于区分盲目攻击的情况和半盲攻击、跟随攻击的情况.在盲目攻击情况下,提供服务的端信息上产生的警报SAlert占总警报数Alert的值是极小的,而在半盲或是跟随攻击的情况下,SAlert/Alert的值增大,且在完全掌握跳变规律的情况下接近1.
4.2 跳变策略安全性端信息跳变网络的攻击主要可以分为盲目攻击、半盲攻击、跟随攻击.
盲目攻击的情况下,攻击者不知道通信双方的跳变规律,只能随机选择端信息进行攻击.假设攻击者选择n个端信息进行攻击,跳变端口个数为M,跳变IP为A,一个跳变周期为φ,那么在时间t内,攻击者能持续攻击到目标端信息的概率为
| $ U = {\left( {\frac{n}{{MA}}} \right)^{\frac{t}{\varphi }}} $ | (14) |
其中:概率和端口与IP个数以及跳变时隙有关,所以提高跳变速率和增加备用IP和端口是可以有效降低攻击者持续攻击的概率.
在半盲攻击和跟随攻击的情况下,攻击者已经掌握部分或全部的跳变规律,此时加快跳变时隙或增加备用端信息效果一般,且代价较大.通过添加认证机制,以向指定端信息序列发送指定数据包的方式,增加系统的安全性.数据包的形式可以描述为
| $ {\rm{packet = \{ }}{\mathit{Y}_i}\left( {{\rm{info}}} \right),{\mathit{Y}_j}\left( {{\rm{info}}} \right), \cdots {\mathit{Y}_k}\left( {{\rm{info}}} \right)\} $ | (15) |
其中:Y表示端信息节点,i, j…, k为随机值,info为该端信息节点的携带认证信息.攻击者不知道敲门认证方式,是无法通过认证的.同时,通过加强敲门序列的复杂程度和加密发送的认证数据能有效防止敲门包被窃听.
5 原型实验与结果分析针对基于DBN的端信息跳变自适应系统模型,搭建了实验原型系统,配置如表 2所示.
|
|
表 2 实验系统配置 |
在跳变Web服务器中配置了10个IP地址,实验设定10 s为1个收集周期,并分别在无攻击,盲目攻击,跟随攻击情况下收集了2 400条的原始数据.在对原始数据集中特殊数据及坏数据的处理之后,便得到了端信息跳变网络的特征数据集.
5.1 模型性能分析将所有的特征数据集根据实际攻击情况进行标签,并将其分为1 800条训练集和600条测试集,在经过多次实验之后,选定了最优网络参数,并利用测试集进行效果测试.
观察分类的精确率和召回率,将被观察的那一类定义为正类,剩余两类为负类,得到结果见表 3:
|
|
表 3 分类精确率和召回率 |
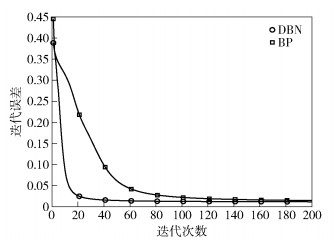
将DBN模型与BP模型的训练效果进行对比,其结果如图 3所示.
|
图 3 DBN和BP的迭代对比 |
可以看到由于DBN经过RBM网络的预训练,其初始误差比随机初始化的BP网络的初始误差要低,而且,DBN的误差下降速度更快,效率更高.另一方面,普通BP网络的误差值最终近似于停留在0.012,而DBN网络最终近似停留在0.011,可见DBN的误差更小,准确率更高.
针对网络状态预测的性能,分别选取最近80、60、40、20、10个周期的网络状态数据进行预测,计算转移概率矩阵,并以此预测下一周期的网络状态值,网络评估数据随着时间推移不断更新.总共测试了400次,不同选取个数的预测情况如表 4所示,可见选取的数据个数为20时,预测准确率达到最高的81.50%.
|
|
表 4 不同选取数据个数的预测情况 |
笔者主要探究了2种异构的跳变策略,并通过实验验证了其安全性.当预测结果为盲目攻击时,加快跳变系统的跳变速率;当预测结果为半盲或跟随攻击时,说明攻击者掌握或部分掌握攻击规律,转而采用一种端信息跳变的扩展认证模式[17].
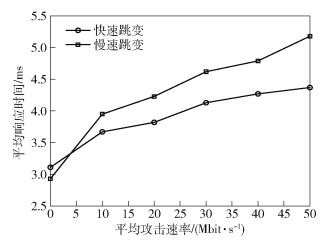
盲目攻击情况下,发起不同速率的TCP-Flood攻击,攻击下快速跳变模式和慢速跳变模式的服务器响应时间如图 4所示.由图可见,随着盲目攻击速率的增加,快速跳变模式下的服务器响应时间趋于平缓,而慢速跳变的服务器响应时间趋于增长且响应时间更长,由此可见加快跳变速率在盲目攻击下具有良好的抵御能力.
|
图 4 盲目攻击下服务器响应时间 |
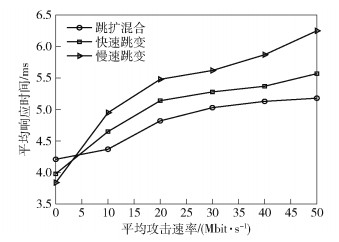
在跟随攻击情况下,发起不同速率的TCP-Flood跟随攻击,在攻击下采用跳扩混合认证模式,快速跳变模式和慢速跳变模式的服务器响应时间如图 5所示.
|
图 5 跟随攻击下服务器响应时间 |
由图 5可见,随着跟随攻击的速率的增加,快速跳变模式相比慢速跳变模式的整体服务器响应时间更短,防护效果更好;跳扩混合模式相比快速跳变模式的整体服务器响应时间更短,且响应时间趋于平缓.由此说明了在跟随攻击的情况下,跳扩混合模式防护效果显著.同时也说明了选取多样异构的跳变策略的重要性.
5.3 对比实验分析笔者将文献[11-12]中的方法和提出的模型进行了对比攻击实验.实验包含正常情况,盲目攻击情况和跟随攻击情况3种场景,每种场景进行30次,攻击类型包括扫描攻击,sql注入, DoS攻击等攻击类型.实验结果显示,共90次实验,文献[11]识别错误次数为11次,文献[12]识别错误次数为9次(由于该文献并未区分盲目攻击和跟随攻击,故该识别是按正常情况和异常情况来区分),笔者所提出的模型识别错误次数为4次.实验结果如表 5所示.可以看到,笔者所提出的模型具有较好的跳变网络状态评估效果,而有效地抵御攻击是建立在正确地评估网络状态基础之上的.
|
|
表 5 不同模型的网络状态评估精确率对比 |
在抗攻击性方面,文献[11-12]所采取的防御措施本质上是根据网络状态的判断情况改变跳变的算法,即改变跳变时隙或者跳变端信息范围,这实际上仍是同一种模式的跳变策略,在跟随攻击时延变小时,就必须考虑减小跳变时隙,但是过小的跳变时隙又会影响正常服务的服务性.
笔者所采用的是异构的跳变策略,在遇到半盲或跟随攻击时采用身份认证的跳扩混合模式,在抗攻击性方面,单纯改变跳变算法仍然有被跟随攻击的风险,而在攻击者无法知道认证方式的前提下,是无法和服务端进行交互的,从而保证了服务器不被跟随.
在服务性方面,过于依靠缩短跳变时隙的方式会导致服务性变差,一次完整的交互时间St是需要小于等于跳变时隙t才能完成一次服务,即St≤t, 但缩短跳变时隙将使得St被限制在较小的时间内,很多服务没法完成.笔者采用的身份认证是利用UDP服务实现,速度快,耗时短,身份认证时间Rt并不影响服务时间St,故跳变时隙t有较大的自由度从而提高模型服务性.
6 结束语主动网络防御在近年来引起了产业界和学术界的广泛关注,它通过动态化、随机化、主动化的特点构建具有依据任务需求、主动变迁网络运行与传输环境的网络架构,从而提高网络攻击的难度,扭转防御者在网络对抗中的不利地位.
笔者对端信息跳变技术中的自适应跳变策略展开研究,给出了跳变策略的自适应跳变方案,进而提出了一种基于深度信念网络的自适应端信息跳变模型,相比于传统的自适应策略,该方法采用DBN深度学习和马尔可夫链的网络评估和预测方式,且选择了异构的主动防御方法,使得结果更具准确性和安全性.同时本文对特征选取的有效性和跳变策略的安全性进行了理论分析,并进行了原型实验,证明了方法的安全有效.
| [1] |
石乐义, 贾春福, 吕述望. 基于端信息跳变的主动网络防护研究[J]. 通信学报, 2008, 29(2): 106-110. Shi L Y, Jia C F, Lv S W. Research on end hopping for active network confrontation[J]. Journal on Communications, 2008, 29(2): 106-110. DOI:10.3321/j.issn:1000-436X.2008.02.016 |
| [2] |
Jajodia S, Ghosh A K, Swarup V, et al. Moving target defense:creating asymmetric uncertainty for cyber threats[M]. [s.l.]: Springer Science & Business Media, 2011: 99-107.
|
| [3] |
Venkatesan S, Albanese M, Amin K, et al.A moving target defense approach to mitigate DDoS attacks against proxy-based architectures[C]//IEEE Conference on Communications and Network Security (CNS).[S.l.]: IEEE, 2016: 198-206.
|
| [4] |
Wang S, Zhang L, Tang C.A new dynamic address solution for moving target defense[C]//Information Technology, Networking, Electronic and Automation Control Conference, IEEE, 2016: 1149-1152.
|
| [5] |
邬江兴. 网络空间拟态防御研究[J]. 信息安全学报, 2016, 1(4): 1-10. Wu J. Research on cyber mimic defense[J]. Journal of Cyber Security, 2016, 1(4): 1-10. |
| [6] |
Hu H, Wu J, Wang Z, et al. Mimic defense:a designed-in cyber security defense framework[J]. IET Information Security, 2018, 12(3): 226-237. DOI:10.1049/iet-ifs.2017.0086 |
| [7] |
仝青, 张铮, 张为华, 等. 拟态防御Web服务器设计与实现[J]. 软件学报, 2017, 28(4): 883-897. Tong Q, Zhang Z, Zhang W H, et al. Design and implementation of mimic defense Web server[J]. Journal of Software, 2017, 28(4): 883-897. |
| [8] |
王禛鹏, 扈红超, 程国振. 一种基于拟态安全防御的DNS框架设计[J]. 电子学报, 2017(11): 2705-2714. Wang Z P, Hu H C, Cheng G Z. A DNS architecture based on mimic security defense[J]. Acta Electronica Sinica, 2017(11): 2705-2714. DOI:10.3969/j.issn.0372-2112.2017.11.018 |
| [9] |
雷程, 马多贺, 张红旗, 等. 基于网络攻击面自适应转换的移动目标防御技术[J]. 计算机学报, 2018(5): 1110-1131. Lei C, Ma D H, Zhang H Q, et al. Moving target defense technique based on network attack surface self-adaptive mutation[J]. Chinese Journal of Computers, 2018(5): 1110-1131. |
| [10] |
Ma D, Lei C, Wang L, et al.A self-adaptive hopping approach of moving target defense to thwart scanning attacks[C]//International Conference on Information and Communications Security.Springer, Cham, 2016: 39-53.
|
| [11] |
赵春蕾.端信息跳变系统自适应策略研究[D].南开大学, 2012.
|
| [12] |
刘江, 张红旗, 代向东, 等. 基于端信息自适应跳变的主动网络防御模型[J]. 电子信息技术学报, 2015, 37(11): 2642-2649. Liu J, Zhang H Q, Dai X D, et al. A proactive network defense model based on self adaptive end hopping[J]. Journal of Electronics & Information Technology, 2015, 37(11): 2642-2649. |
| [13] |
Hinton G E, Osindero S, Teh Y W. A fast learning algorithm for deep belief nets[J]. Neural Computation, 2006, 18(7): 1527-1554. DOI:10.1162/neco.2006.18.7.1527 |
| [14] |
邹国锋, 傅桂霞, 王科俊, 等. 自适应深度卷积神经网络模型构建方法[J]. 北京邮电大学学报, 2017, 40(4): 98-103. Zou Guofeng, Fu Guixia, Wang Kejun, et al. Construction method of adaptive deep convolutional neural network model[J]. Journal of Beijing University of Posts and Telecommunications, 2017, 40(4): 98-103. |
| [15] |
Lu N, Li T, Ren X, et al. A deep learning scheme for motor imagery classification based on restricted boltzmann machines[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2017, 25(6): 566-576. DOI:10.1109/TNSRE.2016.2601240 |
| [16] |
Salah K, Kahtani A. Performance evaluation comparison of snort NIDS under Linux and Windows server[J]. Journal of Network & Computer Applications, 2010, 33(1): 6-15. |
| [17] |
温晓.基于端信息跳扩混合的主动网络防御研究[D].中国石油大学(华东), 2017.
|


