2. 西北工业大学 机电学院, 西安 710072;
3. 东莞市三航军民融合创新研究院, 广东 东莞 523808
针对异常声音识别率低和算法复杂度高等技术难题,提出了一种基于粒子群优化粒子滤波(PSO-PF)算法优化支持向量机(SVM)的识别方法.将PSO算法引入粒子滤波中,通过不断更新粒子速度和位置,使粒子群向高似然后验概率区域移动,提高粒子滤波的参数估计精度.将PSO-PF算法应用于SVM参数优化中,可解决现有SVM参数优化算法易陷入局部最优值等问题.实验结果表明,将所提方法应用于多类异常声音识别,能够有效提高识别率,降低算法复杂度.
2. School of Mechanical Engineering, Northwestern Polytechnical University, Xi'an 710072, China;
3. Dongguan Sanhang Civil-military Integration Innovation Institute, Guangdong Dongguan 523808, China
In order to solve the problems of low recognition accuracy and high computation complexity in abnormal sound signals, a particle filter based on particle swarm optimization (PSO-PF) algorithm is proposed to optimize the parameters of support vector machine (SVM). To improve the estimation precision of particle filter, the particle swarm optimization is applied to drive all the particles to the regions in which their likelihoods are high, by updating the velocity and position of particles constantly. And the algorithm can avoid falling into local optimum in SVM parameter optimization. The experimental results show that the new algorithm can achieve higher recognition accuracy and lower computation complexity for abnormal sounds recognition.
当前国土安全监控系统大多数仅基于视频监视技术,随着社会对监控系统性能和要求的不断提高,传统的视频监控系统显露出私密性低、存储需求大、易受环境影响等诸多局限性,因此利用声音检测作为补充信息来检测和分析公共场所安全事件的研究逐渐受到人们的关注[1],异常声音(枪声、爆炸声等)识别成为音频事件检测领域的一个重点研究方向.
常见的识别技术一般有隐马尔可夫模型、高斯混合模型、支持向量机(SVM, support vector machine)和神经网络等.在众多识别算法中,由于SVM具有小样本、非线性以及高维度识别的特点,在图像分类和语音识别等诸多分类领域中得到了广泛的应用[2].
然而,SVM存在分类性能依赖参数设置的问题,其中惩罚因子和核参数的取值对SVM的分类性能有很大影响,因此,Chapelle[3]等提出了SVM参数优化的概念.常见的SVM参数优化算法有网格搜索算法、梯度下降法和智能优化算法等.利用前两种方法对SVM的参数选择都存在算法复杂度较高、鲁棒性差等缺点.智能优化算法作为一种新型的参数优化算法,目前已有很多研究者将其应用于SVM参数的优化选择[4],如遗传算法(GA, genetic algorithm)[5]、粒子群优化(PSO, particle swarm optimization)算法[6]和蚁群优化算法[7]等.利用此类算法优化SVM参数存在收敛速度慢、易陷入局部最优值等问题.粒子滤波(PF, particle filter)作为一种新型滤波方法能够解决非线性及非高斯系统最优估计问题[8],被广泛应用于系统状态预测和参数估计等领域,但其存在权值退化、粒子贫化和计算效率低等问题.
针对上述问题,笔者提出了基于智能优化算法思想的粒子滤波算法——粒子群优化算法优化粒子滤波(PSO-PF)用于优化SVM模型,将该模型应用于异常声音识别中,解决了识别率低和算法复杂度高等问题.通过与几种常见的优化SVM算法进行仿真比较,验证了基于PSO-PF的SVM参数优化算法在异常声音识别中的优势.
1 PSO-PF算法 1.1 PF算法PF算法是一种基于蒙特卡罗模拟和贝叶斯估计的滤波算法[9].该算法通过一组粒子集{xti, ωti}i=1N对条件后验概率密度函数进行近似,从而获得状态的最小方差估计.其中,条件后验概率函数为
| $ p\left( {{\mathit{\boldsymbol{x}}_t}|{\mathit{\boldsymbol{y}}_{1:t}}} \right) \approx \sum\limits_i^N {\omega _t^i\delta \left( {{\mathit{\boldsymbol{x}}_t}-\mathit{\boldsymbol{x}}_t^i} \right)} $ | (1) |
其中:δ(·)为狄拉克函数;xt为时刻t的状态集;y1:t为时刻1到t的观测集;ωti为时刻t对应粒子xti的权重.时刻t的迭代权重函数为
| $ \omega _t^i = \omega _{t-1}^i\frac{{p\left( {{\mathit{\boldsymbol{y}}_t}|\mathit{\boldsymbol{x}}_t^i} \right)p\left( {\mathit{\boldsymbol{x}}_t^i|\mathit{\boldsymbol{x}}_{t-1}^i} \right)}}{{q\left( {\mathit{\boldsymbol{x}}_t^i|\mathit{\boldsymbol{x}}_{t-1}^i, {\mathit{\boldsymbol{y}}_{1:t}}} \right)}} $ | (2) |
工程应用中[10],一般选取满足q(xti|xt-1i, y1:t)opt=p(xti|xt-1i)条件的重要性函数,对权重归一化处理,粒子的状态估计可写为
| $ {\mathit{\boldsymbol{\hat x}}_t} \approx \sum\limits_{i = 1}^{N-1} {\bar \omega _t^i\mathit{\boldsymbol{x}}_t^i} $ | (3) |
传统的PF算法存在权值退化现象,这意味着模型过分依赖个别权重较大的粒子,从而无法准确描述真实状态,降低了算法鲁棒性.重采样步骤的引入在一定程度上解决了权值退化问题,但该步骤仅复制大权值样本,而直接舍弃小权值粒子,降低了粒子多样性,导致粒子贫化现象[11],特别是在噪声非常小的状态过程中,其会导致所有粒子在经过多次迭代更新后坍塌到一个点.因此,如何在重采样步骤后保持粒子的多样性是实际应用PF的关键[12].
1.2 PSO算法PSO是由Kennedy和Eberhart[13]提出的基于鸟类群体社会行为的智能优化算法.在PSO中,每个解决方案都是搜索空间中的“鸟”,又称为粒子.每个粒子都有对应的适应值,由适应度函数进行评估优化,并指导粒子飞行速度和位置[14],直至找到最优参数.假设搜索空间维度是D且粒子数是N,对任意粒子i=1, 2, …, N,在时刻t的速度和位置分别为vit={vi1, vi2, …, viD}和xit={xi1, xi2, …, xiD},第d维粒子速度和位置的更新公式为
| $ \begin{array}{l} {v_{id}}\left( {t + 1} \right) = w{v_{id}}\left( t \right) + {c_1}{\rm{rand}}\left( {} \right)\left[{{x_{i, {\rm{best}}}}\left( t \right)-{x_{id}}\left( t \right)} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{c_2}{\rm{rand}}\left( {} \right)\left[{{x_{g, {\rm{best}}}}\left( t \right)-{x_{id}}\left( t \right)} \right] \end{array} $ | (4) |
| $ {x_{id}}\left( {t + 1} \right) = {x_{id}}\left( t \right) + {v_{id}}\left( {t + 1} \right) $ | (5) |
其中:xid(t)和vid(t)分别为粒子i在第t次迭代处的位置与速度分量;xid, best(t)为目前为止粒子i已经达到的最佳位置;xdg, best(t)为毗邻粒子i的任意粒子所达到的最佳位置. c1和c2为学习因子;w为惯性权值;rand()为在[0, 1]范围内产生均匀分布的随机数.
PSO算法群移动的启发式策略使得在参数寻优时有效且高效.然而,PSO算法并不是所有优化问题都具有通用性.在解决复杂多峰优化问题时,所有粒子聚集在最优粒子附近,使得粒子群在解空间内无法重新搜索,易陷入局部最优中,出现早收敛现象.
1.3 PSO-PF算法原理考虑到智能算法在处理组合优化方面的优越性,笔者利用PSO算法对PF算法的重采样步骤进行优化,通过PSO算法不断更新粒子集{zti}i=1N,使粒子群向似然概率高的区域移动,从而获得更为准确的状态估计[15].在PSO-PF算法中,首先根据PSO算法定义系统的动态函数为
| $ \mathit{\boldsymbol{z}}_t^i \approx \left[\begin{array}{l} \mathit{\boldsymbol{x}}_i^t\\ \mathit{\boldsymbol{v}}_i^t \end{array} \right] + \left[\begin{array}{l} {\mathit{\boldsymbol{\varepsilon }}_x}\\ {\mathit{\boldsymbol{\varepsilon }}_v} \end{array} \right] $ | (6) |
其中:εx为表示系统噪声;εv为过程噪声.观测函数的定义需要根据具体问题具体分析,观测函数定义为
| $ L\left( {{\mathit{\boldsymbol{z}}_T}} \right)\exp \left[{-\frac{1}{{2{R_k}}}{{\left( {{\mathit{\boldsymbol{z}}_{{\rm{new}}}}-{\mathit{\boldsymbol{z}}_{{\rm{pred}}}}} \right)}^2}} \right] $ | (7) |
其中:Rk为观测噪声,znew为最新测量值,zpred为预测值.为了使PSO-PF算法在搜索过程中能够根据搜索需要动态调整算法的全局与局部寻优能力,惯性权重w的值应该随着迭代的进行做出相应变化.将惯性权重w设置为
| $ w = {w_{\max }}-\frac{{{w_{\max }}-{w_{\min }}}}{{{t_{\max }}}}t $ | (8) |
其中:wmax和wmin分别为惯性权重的最大值和最小值;tmax为最大迭代次数,t为当前迭代次数.
PSO算法与PF算法结合,一方面,可以改善粒子的分布状况,加快粒子集的收敛速度;另一方面,可以减轻PF算法中的粒子贫化现象,使PF算法通过少量粒子就可以对系统状态进行准确估计.
2 SVM参数优化SVM是由Vapnik[3]引入的监督机器学习算法,与其他机器学习算法一样,在SVM模型的应用方面,首先面临的问题是如何选择算法的参数以得到最好的分类性能.由于SVM的理论基础是统计学理论,但其应用相对较少,目前并没有统一的模型参数选取标准.研究表明,在应用SVM模型进行分类时,模型的性能主要受核参数g和惩罚因子C的影响[16].核参数g影响样本数据在高维特征空间中的分布复杂度,惩罚因子C影响机器学习置信范围和经验风险的比例.因此,随着SVM的发展,研究其参数选择的算法具有重要的实际意义.在核函数取径向基的基础上,采用PSO-PF算法来优化SVM参数:核参数g和惩罚因子C.用二维向量{C, g}来表示一个粒子,以5折交叉验证识别率作为粒子的适应度函数.基于PSO-PF算法的SVM参数优化的具体实现步骤如下:
步骤1 将待优化参数C和g设定为粒子的分向量且粒子的维数为二维,设置C和g的约束范围.
步骤2 通过随机采样来初始化粒子样本集{zti}i=1N、个体最优值和全局最优值,初始化各粒子权重为
步骤3 根据系统的动态函数来进化粒子集{zti}i=1N,然后计算进化后每个粒子的权重ωti∝ωt-1iL(zti),为区别于惯性权重w,用ω来表示粒子权重.
步骤4 根据式(4)和式(5)更新粒子的速度和位置,计算更新后每个粒子的适应值,根据粒子的适应值更新个体最优值和全局最优值.
步骤5 对更新后的粒子进行重采样.
步骤6 判断迭代结束条件是否满足,若满足,则输出最优值{zt}={C, g},否则,迭代次数t+1,返回到步骤3继续执行.
3 异常声音识别的实例分析实验所用的异常声音信号来源于China Webmaster网站,包括枪声、爆炸声、玻璃破碎声、尖叫声和脚步声5种.实验均在配置为Intel(R) Pentium(R) CPU G3250、4 GB RAM、Windows7操作系统的计算机上进行.为了验证基于PSO-PF算法的SVM参数优化算法的性能,将其与基于PSO算法的SVM参数优化算法和基于GA的SVM参数优化算法进行对比分析,分别标记为PSO-PFSVM、PSOSVM和GASVM.由于该音频库中的音频本身包含环境噪声,故在采集音频数据时首先需对其进行预处理.具体有端点检测、预加重1-0.97z-1和加窗(Hamming窗,帧长46.43 ms,帧移11.6 ms)步骤.本文采用EEMD和MFCC、短时能量及能量比相结合的特征,构成17维的特征矢量序列.
实验仿真参数如下:惯性权重wmax取1.2,wmin 取0.8,PSO算法中w取1,学习因子c1=c2=2,最大进化代数N为200次,粒子数量为20,Rk取5,选择5折交叉验证识别率作为适应度函数,选择最大进化代数作为算法的迭代结束条件.设置2个待优化参数的范围为:C∈[0.1, 1 000],g∈[0.1, 10 000].
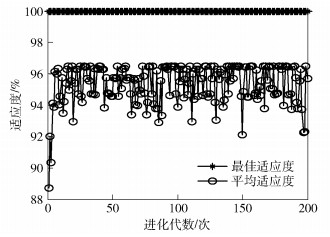
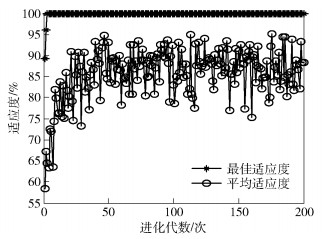
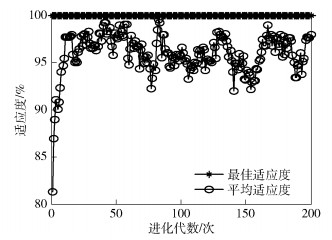
3.1 参数优化过程通过仿真实验来探讨GA、PSO算法和PSO-PF算法3种SVM参数优化算法的优化过程,主要分析了最佳适应度和平均适应度与进化代数之间的关系.仿真结果如图 1~图 3所示,3种优化算法的最佳适应度均可达到100%.在进化初期,各算法的平均适应度随着进化代数的增加而增加,当达到一定的进化代数后,平均适应度在一定的适应度范围内上下波动. 3种算法中,GA的平均适应度上下波动幅度最小,PSO算法次之,PSO-PF算法的平均适应度上下波动幅度最大.这表明GA的局部搜索能力较强,全局搜索能力相对较弱,因此GA在寻优过程中容易陷入局部最优问题,而PSO-PF算法在进化初期全局搜索能力相对较强,随着进化代数的增加,该算法的平均适应度的波动幅度略有减小,局部搜索能力逐渐增强.因此,相比GA和PSO算法,PSO-PF算法不仅能解决易陷入局部最优值的问题,而且还有利于找到参数的全局最优解.
|
图 1 基于GA的SVM参数优化过程 |
|
图 2 基于PSO算法的SVM参数优化过程 |
|
图 3 基于PSO-PF算法的SVM参数优化过程 |
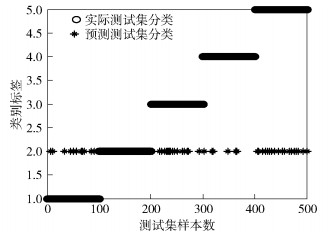
为了分析GA、PSO、PSO-PF 3种优化算法对SVM分类性能的影响,将3种优化算法优化的参数分别代入SVM模型中,对枪声、爆炸声、玻璃破碎声、尖叫声和脚步声5种异常声音进行识别.不同优化算法的分类结果如图 4~图 6所示.
|
图 4 基于GA算法优化的分类结果 |
|
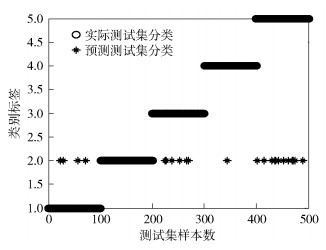
图 5 基于PSO算法优化的分类结果 |
|
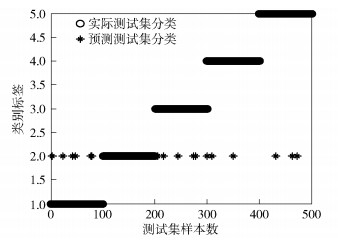
图 6 基于PSO-PF算法优化的分类结果 |
横坐标中1~100代表枪声测试样本,101~200代表尖叫声测试样本,201~300代表玻璃破碎声测试样本,301~400代表爆炸声测试样本,401~500代表脚步声测试样本;纵坐标中类别标签1~5分别代表枪声、尖叫声、玻璃破碎声、爆炸声和脚步声实际样本类别;星号与圆圈完全重合的部分表示正确分类的样本;零散的星号表示错误分类的样本.由于尖叫声属于语音信号,具有周期性且频谱特征明显,因此相比于其他4类非语音信号,尖叫声样本分类识别率最高,故仿真将错误分类显示在标签2上便于观察分析.通过观察可知,基于GA的分类结果中错误分类的样本数最多,基于PSO算法的分类结果中错误分类的样本数次之,基于PSO-PF算法的分类结果中错误分类的样本数最少.这表明基于PSO-PF算法的参数优化算法有助于改善SVM的分类性能,提高异常声音信号识别率.
3.3 参数优化算法对分类复杂度的影响由于粒子的初始状态是随机分布的,为了保证结果的可靠性,实验采样多次运行平均值作为最终的结果,不同优化算法的参数优化结果及消耗时间如表 1所示. 3种算法中,GA在参数优化过程中消耗时间最少,故算法复杂度最低,提出的PSO-PF算法消耗时间较PSO算法消耗的时间要少,对应算法复杂度比PSO算法有所降低.
|
|
表 1 不同优化算法参数优化结果及消耗时间 |
综合分析可知,PSO-PF算法优化SVM在异常声音识别中具有较高的识别率和较低的复杂度.
4 结束语针对异常声音识别问题,笔者提出了一种基于PSO-PF算法优化SVM的识别方法,通过PSO算法改进PF算法的重采样步骤,改善了粒子分布状况,减轻粒子贫化现象,确保使用少量粒子就可以对SVM参数进行准确估计.实验表明,PSO-PF算法一定程度上解决了SVM参数优化易陷入局部最优值的问题,虽然时间复杂度相比GA有所增高,但在异常声音识别应用中,PSO-PFSVM较GASVM和PSOSVM有较高的识别率.因此,从整体性能来看,提出的基于PSO-PF优化SVM参数的算法应用于异常声音识别具有显著优势.
| [1] |
Dan S, Dimitrios G, Emmanouil B, et al. Detection and classification of acoustic scenes and events[J]. IEEE Transactions on Multimedia, 2015, 17(10): 1-1. DOI:10.1109/TMM.2015.2477541 |
| [2] |
周长林, 钱志升, 王勤民, 等. 基于PSO-SVM方法的电源线传导泄漏信号识别与还原[J]. 电子与信息学报, 2018, 40(9): 2207-2211. Zhou Changlin, Qian Zhisheng, Wang Qinmin, et al. Identification of conductive leakage signal in power cable based on multi-classification PSO-SVM[J]. Journal of Electronics and Information Technology, 2018, 40(9): 2207-2211. |
| [3] |
Chapelle O, Vapnik V, Bousquet O, et al. Choosing multiple parameters for support vector machines[J]. Machine Learning, 2002, 46(3): 131-159. |
| [4] |
翟世俊.基于UWB信号的目标识别关键技术研究[D].北京邮电大学, 2014.
|
| [5] |
Li Ke, Wang Lingyu, Wu Jingjing, et al. Using GA-SVM for defect inspection of flip chips based on vibration signals[J]. Microelectronics Reliability, 2018, 81(2): 159-166. |
| [6] |
Wang Yingmin, Cui Tao, Zhang Fujun, et al.Fault diagnosis of diesel engine lubrication system based on PSO-SVM and centroid location algorithm[C]//International Conference on Control, Automation and Information Sciences(ICCAIS).New York: IEEE Press, 2017: 221-226.
|
| [7] |
Zhang Xiaoli, Chen Xuefeng, He Zhengjia. An ACO-based algorithm for parameter optimization of support vector machines[J]. Expert Systems with Applications, 2010, 37(9): 6618-6628. DOI:10.1016/j.eswa.2010.03.067 |
| [8] |
Wang Ershen, Jia Chaoying, Tong Gang, et al. Fault detection and isolation in GPS receiver autonomous integrity monitoring based on chaos particle swarm optimization-particle filter algorithm[J]. Advances in Space Research, 2018, 61(5): 1261-1271. |
| [9] |
Wang Xiangyang, Wang Ying, Wan Wanggen, et al. Object tracking with sparse representation and annealed particle filter[J]. Signal Image and Video Processing, 2014, 8(6): 1059-1068. DOI:10.1007/s11760-014-0628-5 |
| [10] |
Ji Chunlin, Zhang Yangyang, Tong Mengmeng, et al.Particle filter with swarm move for optimization[C]//International Conference on Parallel Problem Solving from Nature.Berlin: Springer, 2008: 909-918.
|
| [11] |
Chen Zhimin, Qu Yuanxin, Liu Bing, et al. Improved multiple model target tracking algorithm based on particle filter[J]. Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 2015, 230(4): 747-759. |
| [12] |
Zhang Gongyuan, Cheng Yongmei, Yang Feng, et al.Particle filter based on PSO[C]//International Conference on Intelligent Computation Technology and Automation.New York: IEEE Press, 2008: 121-124.
|
| [13] |
Kennedy J, Eberhart R, et al.Particle swarm optimization[C]//Proceedings of IEEE International Conference on Neural Networks.Perth: IEEE Xplore, 1995: 1942-1948.
|
| [14] |
Zhao Zengshun, Feng Xiang, Lin Yanyan, et al. Improved Rao-Blackwellized particle filter by particle swarm optimization[J]. Journal of applied mathematics, 2013(5): 302170-1-302170-8. |
| [15] |
Wang Eershen, Li Rui, Pang Tao, et al.Research on GPS RAIM algorithm using PF based on PSO[C]//China Satellite Navigation Conference (CSNC) 2016 Proceedings.Berlin: Springer, 2016: 199-210.
|
| [16] |
Zhou Zhiyu, Zhang Ruoxi, Wang Yaming, et al. Color difference classification based on optimization support vector machine of improved grey wolf algorithm[J]. Optik, 2018, 170: 17-29. DOI:10.1016/j.ijleo.2018.05.096 |


