针对现有信任感知路由协议中信任模型较为简单且能耗优化不足的问题,提出了一种基于信任与能耗均衡的安全分簇路由协议(SCR-TBE).采用模糊综合评判模型并引入多种评判因素计算直接信任,根据偏离度对推荐信任进行过滤与权重分配,并在计算综合信任时考虑历史信任.同时设计簇头惩罚系数,加快恶意簇头的识别与隔离的速度.通过划分监控区域进行非均匀分簇,缓解能量空洞现象.将节点信任值、剩余能量以及数据传输距离作为路由选择因素.设计入簇函数与转发函数,降低恶意节点参与数据传输的几率.仿真结果表明,所提协议与LEACH-C协议和TLES协议相比,数据包数目与能耗均衡性均得到较大提高,提升了无线传感器网络的安全性与可靠性.
Aiming at the problems that the trust model is simple and the energy consumption is not optimized enough in the existing trust-aware routing protocols. A secure clustering routing protocol based on trust and balancing energy consumption (SCR-TBE) is proposed. Introducing multiple evaluation factors, direct trust is calculated by fuzzy comprehensive evaluation model, and the recommendation trust is filtered and weighted allocation based on the deviation degree, and comprehensive trust is calculated added historical trust value. And the cluster head penalty coefficient is designed to speed up the identification and isolation of malicious cluster heads. By dividing the monitoring area, the unequal clustering is achieved to alleviate the energy hole phenomenon. The node trust value, dump energy and data transmission distance are chosen as routing factors. The cluster function and forwarding function are designed to reduce the chance of malicious nodes participating in data transmission. Simulation results show that, compared with LEACH-C and TLES protocols, both the number of data packets and the energy consumption balance have been greatly improved, enhancing the security and reliability of wireless sensor networks.
目前,无线传感器网络(WSNs,wireless sensor networks)中基于分簇的路由协议大都以降低节点能耗为目标,并假设网络中不存在内部恶意节点.如果这些恶意节点长期存在于网络中或者频繁成为簇头,都将对无线传感器网络的正常运转带来巨大的影响[1].因此,设计一种同时考虑节点信任与能耗均衡的安全分簇路由协议显得尤为必要.
但是,现有的关于无线传感器网络中安全分簇路由的研究还存在一些问题.例如,LEACH-C[2]协议中采用的信任模型还不够完善,在进行信任评估时没有全面考察信任因素,没有考虑簇头遭受敌方俘获而成为一个恶意节点的情况;TLES[3]协议没有充分考虑数据传输过程中的能量空洞现象,对于能量受限的无线传感器网络,如何平衡各节点的能耗从而提升网络生存期是非常重要的.因此,针对上述不足,从保障无线传感网络的路由安全与整体能耗出发,笔者提出了一种基于信任与能耗均衡的安全分簇路由协议(SCR-TBE,secure clustering routing protocol based on trust and balancing energy consumption),从而保障无线传感器网络的安全性和降低网络能耗,延长网络生命周期,实现数据的可靠传输.
1 分簇网络结构假设所有节点被随机放置在正方形监测区域内,且部署以后所有节点都保持静止状态.假设基站位于正方形部署区域的左下角,即位于坐标(0, 0)处. 图 1展示了正方形监测区域被分成3层,其他分层情况(4层、5层等)可依照图 1类推.

|
图 1 网络模型举例 |
采用模糊综合评判模型对各信任因素进行分析,建立信任向量来计算直接信任值.选取4个信任因素,建立直接信任的因素集F={F1, F2, F3, F4}. F1、F2、F3、F4分别表示数据相关性因素、数据包发送速率因素、数据新鲜性因素、成功交互率因素[4-5].
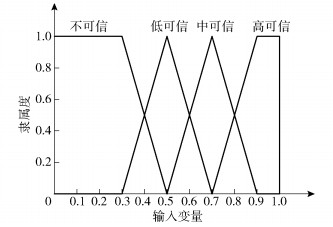
笔者设置了4个程度的模糊子集Ui(i=1, 2, 3, 4)分别表示节点信任的不同程度{不可信,低可信,中可信,高可信}.节点直接信任的模糊综合评判模型的关键步骤是确定信任因素在各信任模糊子集上的隶属度大小.考虑到无线传感器节点物理资源有限,因此选取梯形和三角形表示法构建信任模糊子集的隶属度函数,如图 2所示[6].
|
图 2 输入变量隶属度 |
模糊综合评判模型中的权重向量W=(w1, w2, w3, w4)反映了对各信任因素的关注程度, w1、w2、w3、w分别为4个信任因素的权重,需满足w1+w2+w3+w4=1,不同网络衡量的指标不同,对网络性能的侧重会有所不同,因此可以根据网络的具体应用要求进行针对性设置,为了不失一般性,令w1=w2=w3=w4=
利用合适的模糊合成算子将模糊权重矢量W与隶属度矩阵R合成, 得到各评价对象的模糊综合评价结果向量B,其计算过程如下:
| $ \begin{array}{l} \mathit{\boldsymbol{B}} = \mathit{\boldsymbol{W}} \circ \mathit{\boldsymbol{R}} = \left( {{w_1},{w_2},{w_3},{w_4}} \right) \circ \\ \;\;\;\;\;\;\;\;\left( {\begin{array}{*{20}{c}} {{r_{11}}}&{{r_{12}}}&{{r_{13}}}&{{r_{14}}}\\ {{r_{21}}}&{{r_{22}}}&{{r_{23}}}&{{r_{24}}}\\ {{r_{31}}}&{{r_{32}}}&{{r_{33}}}&{{r_{34}}}\\ {{r_{41}}}&{{r_{42}}}&{{r_{43}}}&{{r_{44}}} \end{array}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {{b_1},{b_2},{b_3},{\mathit{b}_4}} \right) \end{array} $ | (1) |
其中:“°”为模糊合成算子,rij为第i个信任因素Fi对第j个信任评价集Uj的隶属度bi为被评价节点从整体上看对信任评价模糊子集Ui的隶属程度.
本文采用加权平均型的M(·, ⊕)算子,其具有综合程度高、利用R的信息充分、体现权重作用明显的特点[8].根据M(·, ⊕)算子的定义,bk的计算公式如下:
| $ {b_i} = \min \left( {1,\sum\limits_{j = 1}^4 {{w_i}{r_{ji}}} } \right),\mathit{i = }{\rm{1,2,3,4}} $ | (2) |
进一步地,对评价结果向量B进行处理,参考使用模糊向量单值法[8].给4个信任等级依次赋予数值(c1=0.2, c2=0.5, c3=0.7, c4=0.95),则节点i对节点j的直接信任值Ti, j(t)为
| $ {\mathit{T}_{i,j}}\left( t \right) = \frac{{\sum\limits_{k = 1}^n {{c_k}{b_k}} }}{{\sum\limits_{k = 1}^n {{b_k}} }} $ | (3) |
其中:Ti, j(t)为周期t内节点i对节点j的直接信任,bk为信任评判结果,ck为信任等级.
2.2 间接信任间接信任值Ii, j(t)的计算可以表示为
| $ {I_{i,j}}\left( t \right) = R_{i,j}^k\left( \mathit{t} \right)\sum\limits_{k\; \in \;{C_f}} {{w_k}} $ | (4) |
其中:Cf为对共同邻居节点进行筛选后的节点集,wk为某个共同邻居节点k的权值,Ri, jk(t)为邻居节点k对节点j的推荐信任值.
根据信任传递原则[9],某个共同邻居节点k对节点j的推荐信任Ri, jk(t)为
| $ R_{i,j}^k\left( t \right) = {T_{i,k}}\left( t \right){T_{k,j}}\left( t \right) $ | (5) |
其中:Ti, k(t)和Tk, j(t)分别为节点i对节点k的直接信任值和节点k对节点j的直接信任值.
定义共同邻居节点k的推荐信任偏离度dk如下:
| $ {d_k} = \frac{1}{{m - 1}}\sum\limits_{l\;{\rm{ = }}1,\mathit{l} \ne \mathit{k}}^m {\sqrt {{{\left( {R_{i,j}^k\left( t \right) - R_{i,j}^l\left( t \right)} \right)}^2}} } $ | (6) |
如果dk的数值越大,那么节点k的推荐信任是来自恶意节点虚假推荐的几率就越大.为了保障推荐信任的可靠性,设置偏离度门限值ε=0.2,过滤掉偏离度dk>ε的推荐信任值[10].对于dk≤ε的节点,存入集合Cf中.
为了进一步提升间接信任的准确性,提出推荐信任权重分配方案.在集合Cf中的c个节点其偏离程度越小,则推荐信任的权重就越大.定义集合Cf中节点推荐信任的总偏离度D(t)为
| $ D\left( t \right) = \sum\limits_{k\; \in \;{C_f}} {{d_k}\left( \mathit{t} \right)} $ | (7) |
定义集合Cf中节点的总偏离度D(t)与任一偏离度dk(t)之间的数值关系rk(t)为
| $ {r_k}\left( t \right) = D\left( {\mathit{t}} \right)/{d_k}\left( t \right) $ | (8) |
于是,集合Cf中任意节点k的权重wk可通过对rk(t)采取归一化计算得到
| $ {w_k}\left( t \right) = {r_k}\left( t \right)/\sum\limits_{k\; \in \;{C_f}} {{r_k}\left( \mathit{t} \right)} $ | (9) |
最后,将式(9)与式(5)代入式(4)中,则间接信任值Ii, j(t)的计算更新如下:
| $ {I_{i,j}}\left( t \right) = \frac{{{T_{i,k}}\left( t \right){T_{k,j}}\left( t \right)\sum\limits_{k\; \in \;{C_f}} {{r_k}\left( t \right)} }}{{\sum\limits_{k\; \in \;{C_f}} {{r_k}\left( t \right)} }} $ | (10) |
当前综合信任Bi, jc(t)可通过如下公式得到:
| $ B_{i,j}^c\left( t \right) = \varphi {T_{i,j}}\left( \mathit{t} \right) + \theta {I_{i,j}}\left( t \right) $ | (11) |
其中:Ti, j(t)和Ii, j(t)分别为节点i对节点j的直接信任值和节点i对j的间接信任值,φ和θ分别为直接信任权值和间接信任权值,且φ+θ=1.为了公平起见,令φ=θ=0.5[6].
为了防止恶意节点利用持续的正常行为来迅速提高自身信任值,选取上一周期的综合信任值Bi, j(t-1)作为历史因素纳入综合信任Bi, j(t)的计算中.则综合信任Bi, j(t)可按如下公式计算:
| $ {\mathit{B}_{i,j}}\left( t \right) = \left( {1 - \mathit{\lambda }} \right)\mathit{B}_{i,j}^c\left( \mathit{t} \right) + \mathit{\lambda }{\mathit{B}_{{\mathit{i}},j}}\left( {\mathit{t}{\rm{ - 1}}} \right) $ | (12) |
其中:Bi, j(t-1)为前一个周期节点i对节点j的综合信任值,λ为前一周期的综合信任值的权重.
笔者从前后信任差的角度出发,认为当前的综合信任比历史综合信任越高,则λ越接近1,即更多的考虑历史综合信任值;反之,如果当前综合信任比历史综合信任越低,则λ越接近0.自适应权值λ定义为
| $ \mathit{\lambda = }\frac{\alpha }{{1 + {e^{ - \beta {\rm{\cdot}}\Delta \mathit{t}}}}} + \gamma $ | (13) |
其中:ΔT为当前综合信任CTi, jc(t)与上一周期综合信任Bi, j(t-1)的差值,α为权值λ的值域范围,β为权值λ对信任差ΔT的敏感程度,γ为权值λ的最小值,α、β和γ是3个可调节的参数.
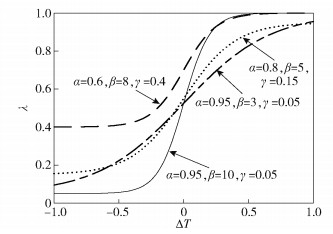
自适应权值λ的函数图像如图 3所示.当信任值上升幅度越大,信任差ΔT就越接近1,λ也会越接近1.即会更多的关注节点的历史信任值,从而抑制信任值的上升速度;反之,当信任值下降时,信任差ΔT将小于0,λ会更接近0,从而会更多的考虑当前的信任值.选取{α=0.95,β=10,γ=0.05},此时更符合信任“增难减易”的性质.
|
图 3 不同参数下的权值λ曲线 |
将λ代入计算综合信任Bi, j(t)的式(12)中,则公式(11)更新如下:
| $ \begin{array}{l} {\mathit{B}_{i,j}}\left( \mathit{t} \right) = \left( {1 - \frac{\alpha }{{1 + {e^{ - \beta {\rm{\cdot}}\Delta T}}}} - \gamma } \right)\mathit{B}_{i,j}^c\left( t \right) + \\ \;\;\;\;\;\;\;\;\left( {\frac{\alpha }{{1 + {\rm{e}^{ - \beta {\rm{\cdot}}\Delta T}}}} + \gamma } \right){\mathit{B}_{i,j}}\left( {\mathit{t}{\rm{ - 1}}} \right) \end{array} $ | (14) |
在分簇结构的无线传感器网络中,考虑到簇头在数据传输的重要性,将根据节点角色给簇头节点定义一个簇头惩罚系数P.节点在计算簇头信任值时,通过乘上簇头惩罚系数P便可加快恶意簇头信任值的下降速度,以此来降低恶意簇头给网络带来的影响.
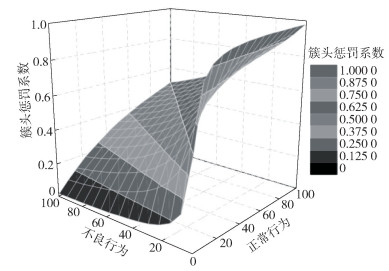
簇头惩罚系数P定义为簇头节点的可靠程度,可引入Beta分布来计算,取值范围在[0, 1]内,如图 4所示.
|
图 4 基于Beta分布概率密度函数的簇头惩罚系数 |
Beta分布概率密度函数的期望为
| $ E\left( \mathit{p} \right) = \frac{\tau }{{\tau + \phi }} $ | (15) |
如果τ和ϕ分别用簇头的正常行为统计a与不良行为统计b表示,即τ=a+1,ϕ=b+1;那么簇头惩罚系数P计算如下:
| $ P = E\left( \mathit{p} \right) = \frac{{a + 1}}{{a + b + 2}} $ | (16) |
如图 1所示,由于基站附近的簇头需要同时收发簇内和簇间数据,所以会出现能量空洞现象[11].因此,首先计算监测区域各层的簇头数,使离基站越近的层拥有越高的簇头比例;然后通过最小化簇间传输总能耗来推导出最优层数;最后根据最优层数与各层簇头数得到簇半径.
3.1 各层簇头数内层簇头节点要承担簇内数据转发与簇间数据转发的任务,因此,第i层区域簇头转发的平均数据量应为其簇内的平均数据量hii和簇间的平均数据量hie之和,第i层簇头的平均数据负担hi的计算公式为
| $ \begin{array}{l} h_i = {h_{ii}} + {h_{ie}} = \\ \frac{{\rho \frac{{S\left( {{i^2} - {{\left( {i - 1} \right)}^2}} \right)}}{{{n^2}}}oh}}{{{e_i}}} + \frac{{\rho \frac{{S\left( {{n^2} - {i^2}} \right)}}{{{n^2}}}oh}}{{{e_i}}} = \\ \;\;\;\;\;\;\frac{{\rho \left( {2i - 1} \right)\frac{S}{{{n^2}}}oh}}{{{e_i}}} + \frac{{\rho \left( {{n^2} - {i^2}} \right)\frac{S}{{{n^2}}}oh}}{{{e_i}}} = \\ \;\;\;\;\;\;\;\;\frac{{\rho \left( {{n^2} - {i^2} + 2i - 1} \right)Soh}}{{{n^2}{e_i}}} \end{array} $ | (17) |
其中:ρ为传感器节点部署的密度,S为整个部署区域的面积,ei为第i层的簇头数,n为正方形部署区域的最优分层数,o表示数据融合率,h为单个节点的数据包大小.
为了平衡各层簇头的数据负担,可令各层簇头的数据负担相等,即
| $ {h_{i} = {h_{i + 1}}},i = 1,2{\rm{\cdot\cdot\cdot,}}\mathit{n}{\rm{ - 1}} $ | (18) |
由式(17)和式(18)可得到相邻两层之间的簇头数比例关系如下:
| $ \begin{array}{l} \frac{{{e_i}}}{{{e_{i + 1}}}} = \frac{{{n^2} - {i^2} + 2i - 1}}{{{n^2} - {i^2}}},i = 1,2{\rm{\cdot\cdot\cdot}},\mathit{n}{\rm{ - 1}}\\ \end{array} $ | (19) |
式(19)表明,确定最远处的第n层的簇头数en,便可依次计算其他各层的簇头数.
| $ {e_n} = \frac{{{f_c}\rho S\left( {2n - 1} \right)}}{{{n^2}}} $ | (20) |
其中fc为第n层区域的簇头比例.
3.2 最优层数由于簇头节点用于发送数据的能量远远高于接收数据的能量,所以通过最小化簇间传输总能耗来计算最优层数n.其中,簇间传输能量开销采用多径衰减模型[12].第i层簇头的平均簇间数据转发能耗为
| $ E_{{\rm{CH}}}^i = {h_i}\left( {{E_{{\rm{elec}}}} + {\varepsilon _{{\rm{amp}}}}d_e^4} \right) $ | (21) |
其中:de为相邻层之间簇头节点的平均距离,di为第i层簇头节点平均的数据负担,Eelec为发送或接收电路的能耗,εamp为多径衰减功率放大参数.
由于节点是均匀分布的,所以de可近似表示为相邻两层之间的几何中心距:
| $ {d_e} = \frac{L}{n} $ | (22) |
其中L为正方形监控区域的边长.
累加式(21),可得到所有簇头在转发簇间数据时所消耗的总能量ECHT如下:
| $ E_{{\rm{CH}}}^T = \sum\limits_{i = 1}^n {{e_i}{h_i}\left( {{E_{{\rm{elec}}}} + {\varepsilon _{{\rm{amp}}}}\frac{{{S^2}}}{{{n^4}}}} \right)} $ | (23) |
然后将式(17)代入式(21)中,ECHT更新如下:
| $ \begin{array}{l} E_{{\rm{CH}}}^T = \sum\limits_{i = 1}^n {\frac{{\rho Soh}}{{{n^2}}}\left( {{E_{{\rm{elec}}}} + {\varepsilon _{{\rm{amp}}}}\frac{{{S^2}}}{{{n^4}}}} \right)} \left( {{n^2} - 1 + 2i - {i^2}} \right) = \\ \;\;\;\;\;\;\;\;\;\frac{{\rho Soh}}{n}\left( {{E_{{\rm{elec}}}} + {\varepsilon _{{\rm{amp}}}}\frac{{{S^2}}}{{{n^4}}}} \right)\left( {\frac{2}{3}{n^2} + \frac{1}{2}n - \frac{1}{6}} \right) \end{array} $ | (24) |
进一步地,计算簇间传输总能耗ECHT对最优层数n的偏导,并令其为0,可得到如下等式:
| $ \frac{{2{\varepsilon _{{\rm{amp}}}}{S^2}}}{{{n^4}}} + \frac{{2{\varepsilon _{{\rm{amp}}}}{S^2}}}{{{n^5}}} - \frac{{5{\varepsilon _{{\rm{amp}}}}{S^2}}}{{6{n^6}}} - \frac{{{E_{\rm{elec}}}}}{{6{n^2}}} = \frac{{2{\mathit{E}_{{\rm{elec}}}}}}{3} $ | (25) |
求如下问题的解可得到区域划分的最优层数n:
| $ \begin{array}{l} \min \mathit{z}\left( n \right) = \left| {\frac{{2{\varepsilon _{{\rm{amp}}}}{S^2}}}{{{n^4}}} + \frac{{2{\varepsilon _{{\rm{amp}}}}{S^2}}}{{{n^5}}} - \frac{{5{\varepsilon _{{\rm{amp}}}}{S^2}}}{{6{n^6}}} - \frac{{{E_{\rm{elec}}}}}{{6{n^2}}} - \frac{{2{\mathit{E}_{{\rm{elec}}}}}}{3}} \right|\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\text{s.t.}\left\{ \begin{array}{l} 1 \le n \le \frac{L}{{{d_0}}}\\ n为整数 \end{array} \right.\; \end{array} $ | (26) |
其中d0为无线传感器在自由空间传播模型下的最大传输距离.
3.3 各层簇半径笔者考虑的都是同构节点,即同一层的簇拥有相同的簇半径[13],则第i层的簇半径Ai为
| $ {A_i} = \sqrt {\frac{{S\left( {2i - 1} \right)}}{{{\rm{ \mathit{ π} }}{n^2}{e_i}}}} $ | (27) |
当所有节点部署后,基站广播“Start”消息,进入初始化阶段. “Start”消息包括最优层数n、各层的簇半径Ai、各层簇头数ei.各节点接收到基站的消息后广播“Hello”消息,包括自身ID号、离基站距离.节点间通过解析“Hello”消息构建本地邻居节点表,包括ID号、基站距离、节点间距离以及节点初始信任值.
4.2 可信簇形成过程1) 通告广播阶段.各层区域节点的门限值函数会生成一个随机数.如果节点ni产生的随机数小于门限值T(ni),则在所属层内广播自己当选簇头的消息.普通节点接收到同层簇头节点的当选消息以后,会根据信号强度来估计簇头节点与自身的距离.
2) 节点入簇过程.鉴于簇头节点在网络中的重要性远大于普通节点,所以除了重点考虑簇头节点的综合信任值以外,还考虑与能量有关的2个因素:剩余能量百分比和簇头距离比.
设某一簇头节点m的综合信任值为Bm,设定一个信任阈值Tth,如果Bm < Tth,那么簇头节点m将不会被普通节点纳入考虑范围.
簇头m的剩余能量百分比ERm指的是剩余能量与初始能量的比例关系,其定义如下:
| $ E_R^m = \frac{{E_{{\rm{curr}}}^m}}{{{E_{{\rm{init}}}}}} $ | (28) |
其中:Ecurrm为节点m的当前剩余能量,Einit为节点的初始能量.
簇头距离比DAm定义为普通节点ni与同层簇头m的距离与所在层的簇半径之比,表达式为
| $ D_A^m = \frac{{Q\left( {{n_i},m} \right)}}{{{\mathit{A}_\mathit{i}}}} $ | (29) |
其中:Q(ni, m)为第i层的某个节点ni到同层簇头节点m的距离,Ai为第i层簇头的簇半径.
综合考虑上述3个因素,本层邻居簇头列表中的某一簇头节点m的入簇函数Jm定义如下:
| $ {J_m} = x{B_m} + yE_R^m + z\left( {1 - D_A^m} \right) $ | (30) |
其中:x为综合信任值的权重,y为剩余能量百分比的权重,z为簇头距离比的权重,且x+y+z=1,x、y、z可根据具体应用环境的安全需求来设定数值,这里令x=0.8,y=0.1, z=0.1.
普通节点收到多个同层簇头发出的当选消息时,首先过滤掉综合信任值低于信任阈值Tth的簇头,将综合信任高于信任阈值Tth的簇头加入本层簇头列表中,然后分别计算列表中各个簇头的入簇函数,选择入簇函数最大的簇头节点,并向此簇头节点发送入簇请求.普通节点在收到簇头发送的确认信息以后,会把此簇头节点作为本地路由表的下一跳地址.
3) 簇的确认.簇头节点收到普通节点的入簇请求后,会首先查找本地信任表,如果低于阈值, 则视其为恶意节点并拒绝入簇;否则各簇头会为每个信任值符合要求的入簇成员分配一个时间片来管理簇成员的数据传输,每个入簇成员便可以在对应的时间片内把感知的数据发给簇头.簇头依次收到所有成员节点的感知数据后,会采用一定的算法来融合数据,并转发给相邻内层簇头.如果是位于第1层的簇头,则直接把数据发给基站.
4.3 可信簇间路由过程第1层的簇头离基站最近,可直接将数据发给基站.而距基站较远的位于第i(1 < i≤n)层的某个簇头节点mi会选择中继节点,按以下2个步骤进行.
1) 簇头节点mi把第i-1层中的簇头存入候选集合Gcandi中,然后依次计算集合Gcandi中的各个第i-1层簇头mi-1作为转发节点的能耗成本K(mi, mi-1),K(mi, mi-1)定义为
| $ K\left( {{m_i},{m_{i - 1}}} \right) = Q{\left( {{m_i},{m_{i - 1}}} \right)^4} + Q{\left( {{m_{i - 1}},BS} \right)^4} $ | (31) |
其中:Q(mi, mi-1)为簇头节点mi、mi-1之间的距离,Q(mi-1, BS)为簇头节点mi-1到基站的距离.
2) 簇头节点mi-1会根据K(mi, mi-1)的大小,从集合Gcandi中选择G个节点存入临时集合Gcandi中G的大小为集合Gcandi中节点数目的一半.然后分别计算集合Gcandi中各节点的转发函数Ij,转发函数Ij定义为
| $ {I_j} = \varepsilon {B_j} + \omega E_R^m + \eta \left( {1 - \frac{{K\left( {{m_i},{m_j}} \right)}}{{\max \left( {K\left( {{m_i},{m_j}} \right)} \right)}}} \right) $ | (32) |
其中:max (K(mi, mj))为Gcandi集合中能耗成本的最大值,j为临时集合Gcandi中的某一节点j,Bj为节点j的综合信任值,ERm为节点j的剩余能量百分比,ε为综合信任值的权重,ω为剩余能量的权重,η为剩余能量的权重.为了能够在重点考察节点信任的同时兼顾能耗均衡,令ε=0.8,ω=0.1,η=0.1.
同时位于内层的簇头节点也要拒绝来信任值小于阈值Tth的转发请求,以免不正常的数据传至基站.
5 仿真结果与性能分析实验使用Matlab2010b对笔者所提SCR-TBE协议与TLES[3]协议和LEACH-C[2]协议的数据传输与能耗均衡进行验证,仿真参数见表 1.设置恶意节点采取选择性转发与开关攻击相结合的方式来攻击网络,当恶意节点是簇头节点时将以80%~100%的几率丢弃接收的数据包,若恶意节点是成员节点将表现和正常节点一致,用于提升其自身的信任值.某些试验场景以及参数会在具体的实验中进行说明.
|
|
表 1 仿真参数设置 |
在验证本文协议数据传输有效性时,考虑丢包率和数据报数目2个指标.
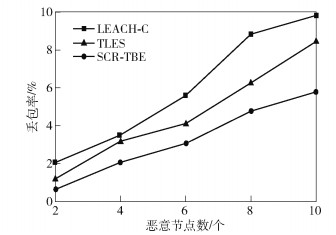
在丢包率实验中,监测区域边长为200 m,节点数目为100个,图 5为3个协议在不同恶意节点个数下的丢包率.随着恶意节点数量的上升,3个协议的丢包率都呈现上升趋势. LEACH-C协议中的信任模型并没有考虑开关攻击,对恶意节点的识别要慢于TLES和SCR-TBE协议,所以其丢包率要高于其他2个协议. SCR-TBE协议性能最好,与TLES协议相比减少了28.2%的丢包率.主要是因为SCR-TBE协议设置了簇头惩罚系数以及信任模型中对推荐信任进行过滤与权重分配,降低恶意节点对间接信任的影响,从而能够更快速地降低恶意节点的信任值并将其隔离出网络.
|
图 5 恶意节点个数与丢包率的关系 |
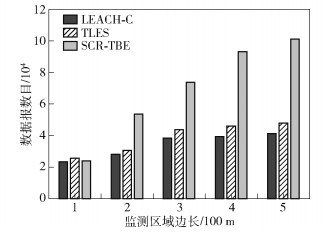
在数据报数目实验中,分别设置不同的监控区域边长,恶意节点个数固定为总节点数的10%,最优层数n依次取值1、2、3、4、5.如图 6所示,随着监测区域的变大,3种协议的数据包数量都呈现上升趋势.而SCR-TBE协议的数据报数目最多,除了在信任计算方面优于其他2种协议,也因为SCR-TBE协议采取了非均匀分簇避免节点的过早死亡,从而大幅提升了数据报数目.而LEACH-C与TLES协议分别采取的是单跳分簇与均匀多跳分簇,数据报数目增长的非常缓慢.
|
图 6 不同监测区域边长下的数据报数目 |
能耗均衡性将从3个方面进行考察:剩余节点数、节点平均剩余能量和网络生存期.
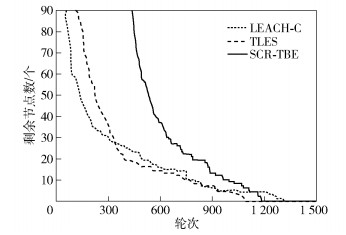
剩余节点数与节点平均剩余能量的实验选取监测面积为200 m×200 m的情形,节点总数为100个,其中设置10%的恶意节点.当边长为200 m时,根据式(26)可得到SCR-TBE协议的最优层数为2. 图 7为3种协议在轮次的剩余节点数情况.随着轮数的增加,3种协议都呈现下降的趋势. LEACH-C协议是单跳形式,所以出现死亡节点的轮次最早. TLES协议采取了多跳传输,出现死亡节点的轮次要慢于LEACH-C,但是没有进行非均匀分簇其所有节点死亡的轮次最早. SCR-TBE协议出现死亡节点的轮次最晚,且出现死亡节点的轮次相对集中.这是因为SCR-TBE协议采取了非均匀分簇策略,根据各区域离基站的大小分配不同的簇头比与簇半径,使得不同区域间的簇头所消耗的能量更加接近.避免了能量空洞效应,均衡节点能耗.
|
图 7 各轮次剩余节点数 |
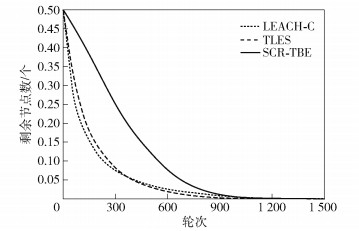
图 8所示为3种协议在各轮次下的节点平均剩余能量.随着轮次的增加,节点平均剩余能量的下降速度都逐渐减慢,且LEACH-C与TLES协议的曲线斜率都呈现由陡逐渐变平滑的趋势,是因为2个都没有平衡各节点的能耗开销,导致部分节点能量消耗过快.而SCR-TBE协议的曲线刚开始则接近于直线,其节点平均剩余能量以比较平稳的速度降低.这是因为SCR-TBE协议通过分析不同区域的簇头数据负担,得到了各区域簇头的迭代关系式,使得不同区域的簇头拥有相同的数据负担.
|
图 8 各轮次节点平均剩余能量 |
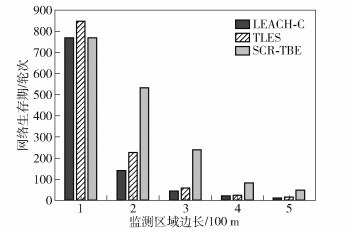
网络生存期定义为正常节点死亡一半时的轮次. 3种协议在不同监测边长下的网络生存期如图 9所示.随着监测区域变大,3个协议的网络生存期都逐渐降低,LEACH-C和TLES协议的下降趋势非常明显,而SCR-TBE协议的下降趋势相对平缓.这是因为随着监测区域边长与节点数目的增加,LEACH-C协议的远端节点在传输数据时所消耗的能量进一步增大;TLES协议中靠近基站的节点所承担的转发数据量随之增长,其能量空洞效应更加凸显. SCR-TBE协议通过非均匀分簇策略避免了多跳分簇协议中的能量空洞效应,在均衡簇头与普通节点能耗的同时,也均衡了各簇头间的能耗.并且SCR-TBE协议通过最优化分层数,减少了区域内簇头所消耗的能量.在此实验中,SCR-TBE协议的网络生存期比TLES协议平均延长了101.4轮.
|
图 9 不同监测区域边长下的网络生存期 |
为了解决无线传感器网络的路由安全问题,设计了一种基于节点信任与能耗均衡的分簇协议(SCR-TBE协议).采用模糊综合评判模型并引入多种评判因素计算直接信任,根据偏离度对推荐信任进行过滤与权重分配,并在计算综合信任时考虑历史信任.设计簇头惩罚系数,加快恶意簇头的识别与隔离的速度.为了缓解多跳分簇协议中的能量空洞现象,通过划分监控区域的方式进行非均匀分簇,将信任值作为一种路由选择因素,结合剩余能量与距离进行入簇选择与簇间路由构建.仿真结果表明,本文协议与对比协议相比,丢包率平均下降了28.2%,网络生存期平均延长了101.4轮,数据包数目与能耗均衡性均都得到了较大提高,加强了安全性和可靠性.
| [1] |
Ishmanov F, Kim S W, Nam S Y. A secure trust establishment scheme for wireless sensor networks[J]. Sensors, 2014, 14(1): 1877-1897. |
| [2] |
Geetha V, Chandrasekaran K. Trust factor based LEACH-C protocol for wireless sensor networks[J]. International Journal of Computer Applications, 2014, 106(18): 43-48. DOI:10.5120/18700-9895 |
| [3] |
Fan Xiangning, Song Yulin.Improvement on LEACH protocol of wireless sensor network[C]//International Conference on Sensor Technologies and Applications.New York: IEEE Press, 2007: 260-264.
|
| [4] |
Liao Hongmei, Ding Shifei. Mixed and continuous strategy monitor-forward game based selective forwarding solution in WSN[J]. International Journal of Distributed Sensor Networks, 2015, 12(1): 1-13. |
| [5] |
Zhang Wei, Zhu Shiwei, Tang Jian, et al. A novel trust management scheme based on Dempster-Shafer evidence theory for malicious nodes detection in wireless sensor networks[J]. The Journal of Supercomputing, 2018, 74(44): 1779-1801. |
| [6] |
姚雷, 王东豪, 梁璇, 等. 无线传感器网络多层次模糊信任模型研究[J]. 仪器仪表学报, 2014, 35(7): 1606-1613. Yao Lei, Wang Donghao, Liang Xuan, et al. Research on multi-level fuzzy trust model for wireless sensor networks[J]. Chinese Journal of Scientific Instrument, 2014, 35(7): 1606-1613. |
| [7] |
刘金鑫.无线传感器网络信任评估模型与方法研究[D].北京: 北京交通大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10004-1015545568.htm
|
| [8] |
谢季坚, 刘承平. 模糊数学方法及其应用(第2版)[M]. 武汉: 华中科技大学出版社, 2000: 128-150.
|
| [9] |
李树江, 佟以鑫, 王向东, 等. 一种基于无线传感器网络安全的能量优化路由算法[J]. 大连理工大学学报, 2016, 56(2): 193-201. Li Shunjiang, Tong Yixin, Wang Xiangdong, et al. An energy-optimization routing algorithm based on security of wireless sensor network[J]. Journal of Dalian University of Technology, 2016, 56(2): 193-201. |
| [10] |
Chen Guihai, Li Chengfa, Ye Mao, et al. An unequal cluster-based routing protocol in wireless sensor networks[J]. Wireless Networks, 2009, 15(2): 193-207. |
| [11] |
杨柳.基于分簇结构的无线传感器网络节能路由协议研究[D].重庆: 重庆大学, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10611-1016765753.htm
|
| [12] |
Chen Zuo, He Min, Liang Wei, et al. Trust-aware and low energy consumption security topology protocol of wireless sensor network[J]. Journal of Sensors, 2015, 23(1): 221-220. |
| [13] |
Yang Liu, Lu Yinzhi, Zhong Yuanchang, et al. An unequal cluster-based routing scheme for multi-level heterogeneous wireless sensor networks[J]. Telecommunication Systems, 2018, 68(1): 11-26. DOI:10.1007/s11235-017-0372-6 |



