2. 华为技术有限公司, 深圳 518129;
3. 中国铁道科学研究院集团有限公司标准计量研究所, 北京 100081
针对多用户-多移动边缘计算服务器系统的动态计算任务卸载问题,基于用户端和服务器端的任务队列模型,以系统的长期平均时延和长期平均功耗为优化目标,求解最优的卸载策略及相应的上行预编码.通过李雅普诺夫优化方法将长期平均问题转化成单阶段目标优化问题,考虑到卸载策略和预编码之间存在范数约束关系,通过连续近似和半正定松弛,可转化成典型的DC规划求预编码解问题.仿真结果表明,所提方案比传统方法具有更低的时延和功耗.
2. Huawei Technologies CO., LTD, Shenzhen 518129, China;
3. Institute of Standard Metrology, China Academy of Railway Sciences, Beijing 100081, China
Considering task queue model on both user and mobile edge computing (MEC) server side, a dynamic computing task offloading problem in multi-user-multi-MEC-server system is proposed. To find the optimal offloading and corresponding uplink precoding strategy, a long-term average overhead containing delay and power consumption of the whole system optimization problem is formulated. The original problem is transformed into a single-stage cost target optimization problem based on Lyapunov optimization method and further converted into a typical DC programming problem by utilizing successive approximation and semi-definite relaxation. Simulation shows that the proposed scheme characterized by optimizing precoding design can meet the lower delay and power consumption requirements.
随着第5代移动通信系统时代的到来,移动设备和节点数量呈现爆炸式增长,同时随着虚拟现实、增强现实、车联网等新兴技术的发展,移动业务在呈现多样化特征的同时对计算资源的需求也日益提升.然而,由于边缘移动设备计算能力和能源存储能力受限,无法执行计算密集型和超高时延要求的新兴业务.为解决这一难题,传统网络架构中,任务被卸载到计算资源丰富的集中式云平台上处理,从而降低移动设备的自身能耗,延长设备的使用时间.然而数据从边缘传输到云端以及计算结果从云端返回到边缘用户的过程会耗费大量时间,任务执行的时延要求将很难满足.此外,大量边缘业务涌向云端会增加网络链路的传输压力和核心网的负担,甚至造成网络瘫痪.针对传统云网络架构中存在的问题,移动边缘计算(MEC, mobile edge computing)应运而生[1],MEC是云计算网络架构的边缘化演进,旨在将计算和存储资源推近到网络的边缘,并进行分布式部署,从而在满足时延要求的同时处理高计算要求的新兴业务.
MEC系统中卸载策略和联合无线电资源优化问题是当前MEC领域的研究热点之一. Wang等[2]针对单个MEC服务器系统提出了用于计算卸载和干扰管理的集成框架;Xu等[3]提出以用户为中心的移动性管理方案,在保证通信能耗约束的前提下最大化单个用户的边缘计算性能;Han等[4]基于随机几何网络建模,研究链路和服务器稳定性约束的系统时延问题,包括通信和排队计算时延,并分析了在轻重负载、不同网络密度等情况下的系统性能.综上,目前国内外很多学者一致认为卸载时延是系统的关键指标,但是多数卸载时延仅考虑通信和计算方面,对由排队所造成的时延研究不足,Han等[4]对排队时延的研究也仅是在下界的推导,未对联合问题进行优化.
笔者提出多用户-多移动边缘计算服务器系统,综合考虑信道状态和任务队列状态变化的马尔可夫特性,以长期平均时延和长期平均功耗的联合优化为目标构建马尔可夫决策问题,利用李雅普诺夫优化方法将系统的稳定性约束条件转化成确定性的约束条件,通过半正定松弛处理,将非凸的确定性优化问题转为凸函数优化,用成熟的凸优化理论求解最优的预编码决策.
1 系统模型多用户的移动边缘计算传输系统如图 1所示.单核移动设备有K个,集合表示为
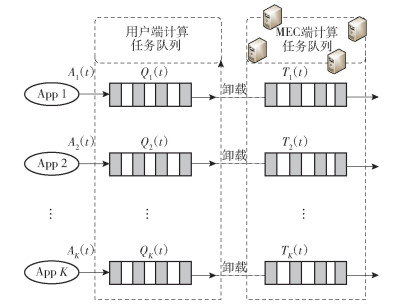
|
图 1 多用户-多移动边缘计算服务器系统模型 |
时刻t,用户端k上存在的任务队列记作Qk(t),用户k卸载到MEC服务器端处理的任务队列记作Tk(t).当用户端产生计算任务时,用户选择将计算任务卸载至MEC服务器端处理或者直接在本地处理,任务卸载调度直接影响本地或MEC服务器端的任务队列状态.若选择在本地处理,将会产生本地功耗;上传至MEC服务器端处理则会产生传输功耗与MEC服务器端计算功耗.
1.1 信道模型令Hk(t)∈CNt×1和Fk(t)∈C1×Nt分别表示在第t个时刻用户k到MEC服务器端的信道编码和预编码.假定在每个决策间隙τ内Hk(t)保持不变,其中每一个元素均服从期望为0、方差为1的标准正态分布,Hk(t)与k相互独立.若给定信道状态信息H={Hk(t):∀k∈
| $ \begin{array}{c} {R_k}\left( {\mathit{\boldsymbol{H}}\left( t \right),\mathit{\boldsymbol{F}}\left( t \right)} \right) = \\ {\alpha _k}\left( t \right)W{\rm{lb}}\left( {1 + \frac{{{{\left| {{{\left( {\mathit{\boldsymbol{H}}\left( t \right)} \right)}^{\rm{H}}}{\mathit{\boldsymbol{F}}_\mathit{k}}\left( t \right)} \right|}^2}}}{{1 + \sum\limits_{i = 1,i \ne k}^K {{{\left| {{{\left( {{\mathit{\boldsymbol{H}}_\mathit{k}}\left( t \right)} \right)}^{\rm{H}}}{\mathit{\boldsymbol{F}}_\mathit{i}}\left( t \right)} \right|}^2}} }}} \right) \end{array} $ |
其中:α(t)={α1(t), α2(t), …, αK(t)}为分配的带宽向量,满足
假设A(t)={Ak(t):k∈
Q(t)={Qk(t):∀k∈
| $ \begin{array}{c} {\mathit{Q}_\mathit{k}}\left( {t + 1} \right) = {\left[ {{Q_k}\left( t \right) - {D_{l,k}}\left( t \right) - {D_{r,k}}\left( t \right)} \right]^ + } + \\ {\mathit{A}_\mathit{k}}\left( t \right),t \in \mathscr{T} \end{array} $ |
其中:[y]+=max{y, 0},Dl, k(t)为用户k在第t个时刻分配到本地处理的计算任务量,它取决于本地CPU此刻的计算能力;Dr, k(t)为t时刻用户k卸载到MEC服务器端的任务量,与传输速率Rk有关.假设卸载策略为Sk(t),Sk(t)=1代表用户k选择将计算任务卸载到MEC服务器端执行,Sk(t)=0表示任务留在本地处理的策略. Dl, k(t)和Dr, k(t)与对应的卸载策略相关,即Dl, k(t)=(1-Sk(t))Dnormall.其中:Dnormall为单位时间内在本地处理的计算任务量,Dnormall=fk/Xl,Xl为衡量用户端CPU运行速度的指标,即处理每比特任务量所需要的CPU周期数,fk为用户端计算频率,且在相当长的时间内恒定不变. Dr, k(t)=Sk(t)Rk(H(t), F(t))τ.
1.3 MEC服务器端任务队列模型令T(t)
| $ {{T}_{k}}\left( t+1 \right)={{\left[ {{T}_{\text{1}}}\left( t \right)-{{D}_{s,k}}\left( t \right) \right]}^{+}}+{{D}_{r,k}}\left( t \right) $ |
其中:Ds, k(t)表示在第t个时隙MEC服务器端处理的来自用户k的计算任务量,Ds, k(t)=fC, m/Xser,Xser为衡量MEC服务器端CPU运行速度的指标,fC, m为MEC服务器端计算频率,在相当长的时间内是恒定值.从MEC服务器端队列表达式可以看出,只有没有处理完的任务量才会被存储在MEC服务器端任务队列中,调节预编码也可以控制MEC服务器端的任务队列长度.对所有用户k,令Qk(0)=Tk(0)=0.
根据信道状态、MEC服务器端及用户端任务队列状态的马尔可夫转移特性,通过最优化预编码决策,用户可以选择将自己的计算任务上传到MEC服务器端或者直接在本地处理,达到优化系统时延的目的.
1.4 本地和MEC服务器端的功耗模型根据文献[5],t时刻,用户k的本地功耗pl, k(t)以及MEC服务器端的计算功耗pser, k(t)分别为
| $ \left. \begin{array}{l} {p_{l,k}}\left( t \right) = \left( {1 - {S_k}\left( t \right)} \right){\mathscr{K}_{{\rm{mob,}}\mathit{k}}}f_k^3\left( t \right),\;\;\;k \in \mathscr{K}\\ {p_{\text{ser},k}}\left( t \right) = {S_k}\left( t \right)\sum\limits_{m \in \mathscr{M}} {{\mathscr{K}_{{\rm{ser,}}\mathit{m}}}f_{C,m}^3\left( t \right),\;\;\;k \in \mathscr{K},m \in \mathscr{M}} \end{array} \right\} $ | (1) |
其中:
系统产生功耗包括2个方面:一是传输功耗;二是在本地以及服务器端处理计算任务产生的计算功耗.系统的平均功耗表达式为
| $ {{\bar P}_\mathit{\Sigma }}\left( t \right) \buildrel \Delta \over = \mathop {\lim }\limits_{T \to + \infty } \frac{1}{T}\sum\limits_{t = 0}^{T - 1} {E\left[ {\sum\limits_{k \in \mathscr{K}} {\left( {{w_\mathit{k}}\left( {{p_{{\rm{tx,}}\mathit{k}}}\left( t \right) + {p_{l,k}}\left( t \right)} \right) + \\ {w_\mathit{M}}{p_{{\rm{ser,}}\mathit{k}}}\left( t \right)} \right)} } \right]} $ | (2) |
其中:wk、wM分别为用户端、MEC服务器端的功耗权重系数,ptx, k(t)表示传输功耗.卸载策略Sk(t)与上行预编码之间存在如下关系:
| $ {S_k}\left( t \right) = \left\| \; \right\|{\mathit{\boldsymbol{F}}_\mathit{k}}\left( t \right){\left\| {^2} \right\|_{{l_0}}} $ | (3) |
其中:‖·‖为2-范数,‖·‖ l0为0-范数.给定信道状态信息H={Hk(t):∀k∈
| $ {{\bar P}_\mathit{\Sigma }}\left( t \right) \triangleq \mathop {\lim }\limits_{T \to + \infty } \frac{1}{T}\sum\limits_{t = 0}^{T - 1} {E\left[ {\sum\limits_{k \in \mathscr{K}} {\left( {{w_k}\left( {{{\left\| {{\mathit{\boldsymbol{F}}_\mathit{k}}\left( t \right)} \right\|}^2} + \\ \left( {1 - \left\| \; \right\|{\mathit{\boldsymbol{F}}_\mathit{k}}\left( t \right){{\left\| {^2} \right\|}_{{l_0}}}} \right){K_{{\text{mob,}}\mathit{k}}}f_k^3\left( t \right)} \right) + \\ {w_M}\left\| \; \right\|{\mathit{\boldsymbol{F}}_\mathit{k}}\left( t \right){{\left\| {^{\text{2}}} \right\|}_{{l_0}}}\sum\limits_{m \in \mathscr{M}} {{\mathscr{K}_{{\text{ser,}}\mathit{m}}}f_{C,m}^3\left( t \right)} } \right)} } \right]} $ |
在无限时域中,时延是衡量系统性能的重要特性之一.通过用户端及MEC服务器端的任务队列长度之和来度量系统的时延特性,可以得到系统的平均时延表达式为
| $ \begin{gathered} {{\bar q}_{\mathit{\Sigma ,k}}}\left( t \right) \triangleq \mathop {\lim }\limits_{T \to + \infty } \frac{1}{T}\sum\limits_{t = 0}^{T - 1} {E\left[ {\sum\limits_{k \in \mathscr{K}} {\left( {{Q_k}\left( t \right) + {T_k}\left( t \right)} \right)} } \right]} , \\ k \in \mathscr{K} \\ \end{gathered} $ |
优化无限时域内系统的平均时延本质上是优化系统的任务队列动态演变趋势.用户可以调节预编码使系统的队列长度向最优的方向演变,这是典型的随机优化模型问题.
2.3 总的优化问题基于系统成本模型分析[6-7],考虑平均功耗和时延的联合优化,总的优化问题数学表达式为
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\mathop {\min }\limits_{\boldsymbol{X}\left( t \right)} {{\bar P}_\mathit{\Sigma }}\left( t \right)\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\mathop {{\rm{lim}}}\limits_{T \to \infty } \frac{1}{T}\sum\limits_{t = 0}^T {\left( {\sum\limits_{k \in \mathscr{K}} {{{\bar q}_{\mathit{\Sigma ,k}}}\left( t \right)} } \right) < \infty } \\ \;\;\;\;\;\;{\theta _k} \ge {\rho _k},\;\forall k \in \mathscr{K} \end{array} $ | (4) |
其中:ρk为信号质量阈值,表示用户任务卸载时的传输质量要求.
整理得单阶段的功耗方程为
| $ c\left( t \right) = \sum\limits_{k \in \mathscr{K}} {\left( {{w_k}\left( {{{\left\| {{\mathit{\boldsymbol{F}}_\mathit{k}}\left( t \right)} \right\|}^2} + {\mathscr{K}_{{\text{mob,}}\mathit{k}}}f_k^3\left( t \right)} \right) + \\ \left( {{w_M}\sum\limits_{m \in \mathscr{M}} {{\mathscr{K}_{{\text{ser,}}\mathit{m}}}f_{C,m}^3\left( t \right) - {w_k}{\mathscr{K}_{{\text{mob,}}\mathit{k}}}f_k^3\left( t \right)} } \right) \times \\ \left\| \; \right\|{\mathit{\boldsymbol{F}}_\mathit{k}}\left( t \right){{\left\| {^2} \right\|}_{{l_0}}}} \right)} $ |
用连续方程近似单阶段功耗方程中的离散函数,其中,
| $ \left\| \; \right\|{\mathit{\boldsymbol{F}}_\mathit{k}}\left( t \right){\left\| {^2} \right\|_{{l_0}}} \approx \mathop {\lim }\limits_{\alpha \to 0} \frac{{\ln \left( {1 + {{\left\| {{\mathit{\boldsymbol{F}}_\mathit{k}}\left( t \right)} \right\|}^2}{\alpha ^{ - 1}}} \right)}}{{\ln \left( {1 + {\alpha ^{ - 1}}} \right)}} $ |
对于充分小的α,有
| $ \left\| \; \right\|{\mathit{\boldsymbol{F}}_\mathit{k}}\left( t \right){\left\| {^2} \right\|_{{l_0}}} \approx \frac{{\ln \left( {1 + {{\left\| {{\mathit{\boldsymbol{F}}_\mathit{k}}\left( t \right)} \right\|}^2}{\alpha ^{ - 1}}} \right)}}{{\ln \left( {1 + {\alpha ^{ - 1}}} \right)}} $ |
成立,则单阶段功耗方程可以进一步重写为
| $ c\left( t \right) \approx \sum\limits_{k \in \mathscr{K}} {\left( {\left( {{w_M}\sum\limits_{m \in \mathscr{M}} {{\mathscr{K}_{{\text{ser,m}}}}f_{C,m}^3\left( t \right) -\\ {w_k}{\mathscr{K}_{{\text{mob,}}\mathit{k}}}f_k^3\left( t \right)} } \right)\frac{{\ln \left( {1 + {{\left\| {{\mathit{\boldsymbol{F}}_\mathit{k}}\left( t \right)} \right\|}^2}{\alpha ^{ - 1}}} \right)}}{{\ln \left( {1 + {\alpha ^{ - 1}}} \right)}} + \\ {w_k}\left( {{{\left\| {{\mathit{\boldsymbol{F}}_\mathit{k}}\left( t \right)} \right\|}^2} + {\mathscr{K}_{{\text{mob,}}\mathit{k}}}f_k^3\left( t \right)} \right)} \right)} $ |
利用李雅普诺夫优化方法[3]对优化问题中的队列稳定性条件做如下处理,令
| $ L\left( {\mathit{\pmb{\Theta} }\left( t \right)} \right) = \frac{1}{2}\sum\limits_{k \in \mathscr{K}} {\left[ {Q_k^2\left( t \right) + T_k^2\left( t \right)} \right]} $ |
其中Θ(t)[Q(t), T(t)].李雅普诺夫加值函数为
| $ \Delta \left( {\mathit{\pmb{\Theta} }\left( t \right)} \right) = L\left( {\mathit{\pmb{\Theta} }\left( {t + 1} \right)} \right) - L\left( {\mathit{\pmb{\Theta} }\left( t \right)} \right) $ |
李雅普诺夫加值惩罚函数为
| $ {\Delta _V}\left( {\mathit{\pmb{\Theta} }\left( t \right)} \right) = \Delta \left( {\mathit{\pmb{\Theta} }\left( t \right)} \right) + VE\left[ {{P_\mathit{\Sigma }}\left( t \right)\left| \mathit{\pmb{\Theta} } \right.\left( t \right)} \right] $ |
其中V为李雅普诺夫控制参数.
对用户端的动态队列Qk2(t+1)做如下不等式处理,其中,DΣ, k(t)=Dl, k(t)+Dr, k(t):
| $ \begin{array}{l} \;\;\;\;Q_k^2\left( {t + 1} \right) = {\left( {{{\left[ {{Q_k}\left( t \right) - {D_{\mathit{\Sigma ,k}}}\left( t \right)} \right]}^ + }} \right)^2} + A_k^2\left( t \right) + \\ \;\;\;\;\;\;\;\;\;\;\;2{A_k}\left( t \right){\left[ {{Q_k}\left( t \right) - {D_{\mathit{\Sigma ,k}}}\left( t \right)} \right]^ + } \le \\ \;\;\;\;{\left( {{Q_k}\left( t \right) - {D_{\mathit{\Sigma ,k}}}\left( t \right)} \right)^2} + A_k^2\left( t \right) + 2{A_k}\left( t \right){Q_k}\left( t \right) \le \\ Q_k^2\left( t \right) - 2{Q_k}\left( t \right)\left( {{D_{\mathit{\Sigma ,k}}}\left( t \right) - {A_k}\left( t \right)} \right) + A_k^2\left( t \right) + D_{\mathit{\Sigma ,k}}^2\left( t \right) \end{array} $ | (5) |
把不等式(5)右边的Qk2(t)移到不等式的左边,整理得
| $ \begin{gathered} \frac{1}{2}\left[ {Q_k^2\left( {t + 1} \right) - Q_k^2\left( t \right)} \right] \leqslant \\ - {Q_k}\left( t \right)\left( {{D_{\mathit{\Sigma },k}}\left( t \right) - {A_k}\left( t \right)} \right) + \frac{{A_k^2\left( t \right) + D_{\mathit{\Sigma },k}^2\left( t \right)}}{2} \\ \end{gathered} $ |
同理,对MEC服务器端的动态队列Tk2(t+1)进行处理:
| $ \begin{gathered} T_k^2\left( {t + 1} \right) \leqslant \\ \;\;\;{\left( {{T_k}\left( t \right) - {D_{s,k}}\left( t \right)} \right)^2} + D_{r,k}^2\left( t \right) + 2{D_{r,k}}\left( t \right){T_k}\left( t \right) \leqslant \\ T_k^2\left( t \right) - 2{T_k}\left( t \right)\left( {{D_{s,k}}\left( t \right) - {D_{r,k}}\left( t \right)} \right) + D_{r,k}^2\left( t \right) + D_{s,k}^2\left( t \right) \\ \end{gathered} $ | (6) |
可得
| $ \begin{array}{c} \frac{1}{2}\left[ {T_k^2\left( {t + 1} \right) - T_k^2\left( t \right)} \right] \le \\ - {T_k}\left( t \right)\left( {{D_{s,k}}\left( t \right) - {D_{r,k}}\left( t \right)} \right) + \frac{{D_{r,k}^2\left( t \right) + D_{s,k}^2\left( t \right)}}{2} \end{array} $ |
综合式(5)和式(6)可得李雅普诺夫加值函数:
| $ \Delta \left( {\mathit{\pmb{\Theta} }\left( t \right)} \right) \le - \sum\limits_{k \in \mathscr{K}} {\left[ {{Q_k}\left( t \right)\left( {{D_{\mathit{\Sigma ,k}}}\left( t \right) - {A_k}\left( t \right)} \right) + \\ {T_k}\left( t \right)\left( {{D_{s,k}}\left( t \right) - {D_{r,k}}\left( t \right)} \right)} \right] + \\ \frac{1}{2}\sum\limits_{k \in \mathscr{K}} {\left[ {A_k^2\left( t \right) + D_{\mathit{\Sigma ,k}}^2\left( t \right) + D_{r,k}^2\left( t \right) + D_{s,k}^2\left( t \right)} \right]} } $ |
同时对不等式两边取数学期望,可得ΔV(Θ(t))上界:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\Delta _V}\left( {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}\left( t \right)} \right) \le \\ C - E\left[ {\sum\limits_{k \in \mathscr{K}} {\left[ {{Q_k}\left( t \right)\left( {{D_{\mathit{\Sigma ,k}}}\left( t \right) - {A_k}\left( t \right)} \right)} \right]\left| {\mathit{\pmb{\Theta} }\left( t \right)} \right.} } \right] - \\ \;\;\;E\left[ {\sum\limits_{k \in \mathscr{K}} {\left[ {{T_k}\left( t \right)\left( {{D_{s,k}}\left( t \right) - {D_{r,k}}\left( t \right)} \right)} \right]\left| {\mathit{\pmb{\Theta} }\left( t \right)} \right.} } \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;VE\left[ {{P_\mathit{\Sigma }}\left( t \right)\left| {\mathit{\pmb{\Theta} }\left( t \right)} \right.} \right] \end{array} $ | (7) |
其中:C为常数,通过优化ΔV(Θ(t))的上界(不等式(7)的右半部分)可以求得近似最优解.则总的优化问题(4)可以转化成综合考虑队列状态和功耗的单阶段优化问题,数学表达式为
| $ \mathop {\min }\limits_F \sum\limits_{k \in \mathscr{K}} {\left[ {\left( {{T_k}\left( t \right) - {Q_k}\left( t \right)} \right){D_{r,k}}\left( t \right) - \\ {Q_k}\left( t \right){D_{l,k}}\left( t \right)} \right] + V{P_\mathit{\Sigma }}\left( t \right)\\ {\rm{s}}{\rm{.t}}\;{\theta _\mathit{k}} \ge {\rho _k},\forall k \in \mathscr{K}} $ | (8) |
其中:PΣ(t)
| $ \begin{matrix} \mathop {\min }\limits_F \,\sum\limits_{k\in \mathscr{K}}{\left\{ V\left( \left( {{w}_{M}}\sum\limits_{m\in \mathscr{M}}{{{\mathscr{K}}_{\text{ser},m}}f_{C,m}^{3}\left( t \right)-\\ {{w}_{k}}{{\mathscr{K}}_{\text{mob,}\mathit{k}}}f_{k}^{3}\left( t \right)+\frac{{{Q}_{k}}\left( t \right)\ D_{\text{normal}}^{l}}{V}} \right)\times \\ \frac{\ln \left( \left. 1+ \right\|{{\mathit{\boldsymbol{F}}}_{\mathit{k}}}\left( t \right)\left\| ^{2}{{\alpha }^{-1}} \right. \right)}{\ln \left( 1+{{\alpha }^{-1}} \right)}+\\ {{w}_{k}}\left( \left| {{\mathit{\boldsymbol{F}}}_{\mathit{k}}}\left( t \right)\left\| ^{2} \right.+{{\mathscr{K}}_{\text{mob,}\mathit{k}}}f_{k}^{3}\left( t \right) \right. \right) \right)-\\ {{Q}_{k}}\left( t \right)\ D_{\text{normal}}^{l}+\left( {{T}_{k}}\left( t \right)-{{Q}_{k}}\left( t \right) \right)\tau {{\alpha }_{k}}\left( t \right)\ W\times \\ \text{lb}\left( 1+\frac{\left| \ \ {{\left( {{\mathit{\boldsymbol{H}}}_{\mathit{k}}}\left( t \right) \right)}^{\text{H}}}{{\mathit{\boldsymbol{F}}}_{k}}\left( t \right)\ \ \left| ^{2} \right. \right.}{1+\sum\limits_{i=1,i\ne k}^{K}{\left| \ \ {{\left( {{\mathit{\boldsymbol{H}}}_{\mathit{k}}}\left( t \right) \right)}^{\text{H}}}{{\mathit{\boldsymbol{F}}}_{\mathit{i}}}\left( t \right)\ \ \left| ^{2} \right. \right.}} \right) \right\}} \\ \text{s}\text{.}\ \text{t}.\sqrt{1+\sum\limits_{i=1,i\ne k}^{K}{\left| \mathit{\boldsymbol{H}}_{\mathit{k}}^{\text{H}}{{\mathit{\boldsymbol{F}}}_{\mathit{i}}}\left| ^{2} \right. \right.}}\le \frac{1}{\sqrt{{{\rho }_{k}}}}\operatorname{Re}\ \left( \mathit{\boldsymbol{H}}_{k}^{\text{H}}{{\mathit{\boldsymbol{F}}}_{\mathit{k}}} \right), \\ \forall k\in \mathscr{K} \\ \end{matrix} $ | (9) |
接下来做半正定松弛处理[8],令Wk=FkFkH,Vk=HkHkH,如果去掉矩阵秩为1的约束,优化方程(9)转化成
| $ \begin{matrix} \mathop {\min }\limits_W \,\sum\limits_{k\in \mathscr{K}}{\left\{ V\left( \left( {{w}_{M}}\sum\limits_{m\in \mathscr{M}}{{{\mathscr{K}}_{\text{ser},m}}f_{C,m}^{3}\left( t \right)-\\ {{w}_{k}}{{\mathscr{K}}_{\text{mob,}\mathit{k}}}f_{k}^{3}\left( t \right)+\frac{{{Q}_{k}}\left( t \right)\ D_{\text{normal}}^{l}}{V}} \right)\times \\ \frac{\ln \left( 1+{{\alpha }^{-1}}\text{Tr}\left( {{\mathit{\boldsymbol{W}}}_{\mathit{k}}} \right) \right)}{\ln \left( 1+{{\alpha }^{-1}} \right)}+{{w}_{k}}\left( \text{Tr}\left( {{\mathit{\boldsymbol{W}}}_{\mathit{k}}} \right)+{{\mathscr{K}}_{\text{mob,}\mathit{k}}}f_{k}^{3}\left( t \right) \right) \right)-\\ {{Q}_{k}}\left( t \right)\ D_{\text{normal}}^{l}+\left( {{T}_{k}}\left( t \right)-{{Q}_{k}}\left( t \right) \right)\tau {{\alpha }_{k}}\left( t \right)\ W\times \\ \text{lb}\left( 1\text{+}\frac{\text{Tr}\left( {{\mathit{\boldsymbol{V}}}_{\mathit{k}}}{{\mathit{\boldsymbol{W}}}_{\mathit{k}}} \right)}{\text{1+}\sum\limits_{\mathit{i}\text{=1,}\mathit{i}\ne \text{k}}^{\text{K}}{\text{Tr}\left( {{\mathit{\boldsymbol{V}}}_{\mathit{k}}}{{\mathit{\boldsymbol{W}}}_{i}} \right)}} \right) \right\}} \\ \text{s}\text{.}\ \text{t}.\sum\limits_{i=1,i\ne k}^{\mathit{K}}{\text{Tr}\left( {{\mathit{\boldsymbol{V}}}_{\mathit{k}}}{{\mathit{\boldsymbol{W}}}_{\mathit{k}}} \right)}-\frac{1}{{{\rho }_{k}}}\text{Tr}\left( {{\mathit{\boldsymbol{V}}}_{\mathit{k}}}{{\mathit{\boldsymbol{W}}}_{\mathit{k}}} \right)\le -1,\forall k\in \mathscr{K} \\ \end{matrix} $ | (10) |
其中:Tr(Wk)为凸函数,含有变量Wk的ln和lb的形式是凹函数.即式(10)可以拆分成一个凸函数和2个凹函数之和,约束条件是线性的凸函数.综上转化分析,最终优化问题是一个典型的DC规划问题,可以用CCP算法[9]求解最优预编码决策.
算法:CCP算法求解{W*}
步骤1 初始化:迭代次数n=0;以式(10)中的凸函数部分为目标求解式(11),作为初始点记作{Wk[0]}.
| $ \begin{matrix} \underset{W}{\mathop{\text{min}}}\,\sum\limits_{k\in \mathscr{K}}{\text{Tr}\left( {{\mathit{\boldsymbol{W}}}_{k}} \right)} \\ {\text{s}.\text{t}.}\sum\limits_{i=1,i\ne k}^{K}{\text{Tr}\left( {{\mathit{\boldsymbol{V}}}_{k}}{{\mathit{\boldsymbol{W}}}_{i}} \right)-\frac{1}{{{\rho }_{k}}}\text{Tr}\left( {{\mathit{\boldsymbol{V}}}_{k}}{{\mathit{\boldsymbol{W}}}_{k}} \right)\le }-1,\forall k\in \mathscr{K} \\ \end{matrix} $ | (11) |
步骤2 n=n+1.
步骤3 更新W:基于{Wk[n]},求解式(10)的一阶泰勒近似问题,得到最优解{W*}.
步骤4 检查{Wk[n]:∀k∈
输出:最优解{W*}.
4 仿真结果与分析Baseline 1 忽略队列信息,只考虑传输功耗最小化的上行预编码策略.
Baseline 2 考虑Cheng等[5]基于最小化瞬时传输和计算功耗和的卸载策略,同时采用迫零预编码算法.
将笔者设计的方案与其他2个典型模型(Baseline1、2)进行性能对比,仿真参数如表 1所示.
|
|
表 1 仿真参数 |
图 2所示为本文方案中系统总功耗、用户端和MEC服务器端任务队列长度与李雅普诺夫控制参数的关系.从该双纵轴图可以看出,李雅普诺夫控制参数增加,系统总功耗随之减少,而队列囤积逐渐增加,这是因为李雅普诺夫控制参数在优化中相当于时延和功耗的权重,该参数越大,即目标更着重优化系统功耗,对时延的关注变小.因此,合理的V值设置有利于取得优化功耗和队列囤积的折中效果.
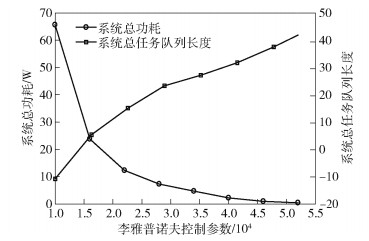
|
图 2 系统总功耗、任务队列长度与李雅普诺夫控制参数关系 |
图 3所示为系统总功耗与用户数量的关系.可见,随着用户任务数量增加,系统总功耗随之增加.本文方案、Baseline 2的系统功耗比Baseline 1低,且在用户数量较多时更明显,这是因为Baseline 1只考虑传输功耗优化,而本文方案和Baseline 2同时优化传输和计算功耗.本文方案的系统功耗比Baseline 2更低,这是因为Baseline 2只关注单阶段瞬时目标优化,忽略队列信息的马尔可夫特性,而本文方案的优化目标是长期平均功耗.可见,笔者所提的预编码设计方案在优化功耗性能方面有较大提升.
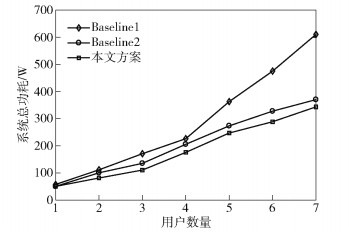
|
图 3 系统总功耗与用户数量关系 |
图 4所示为系统总功耗随天线数量变化的关系.可以看出,随着天线数量增加,系统总功耗减少.这是因为天线数量增加,用户的任务分配有更多选择,MEC服务器端能提供更多服务,减少用户端的能耗负荷,从而降低系统总功耗.本文方案的系统总功耗保持最低,原因与图 3解释类似.同时可以看出,当天线数量由1增至2时,系统总功耗大幅度下降,之后随着天线数量增加,系统总功耗下降趋势趋于平缓,这是由于多天线增益趋于稳定.
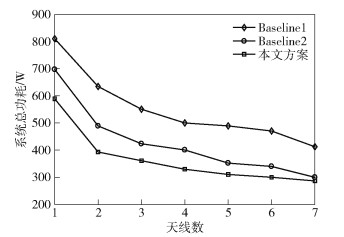
|
图 4 系统总功耗与天线数量关系 |
图 5所示为系统时延和用户数量的关系.随着用户数量的增加,系统时延随之增加.这是因为用户数量增加,需要处理的任务量增多,信道会逐渐拥塞,所以系统时延随之增加.本文方案的系统时延比Baseline 2、Baseline 1小,这是因为本文方案同时考虑信道和队列状态的马尔可夫特性,优化系统长期平均时延,而Baseline 1只优化传输功耗,没有考虑时延特性. Baseline 2考虑时延特性,但是只优化单阶段瞬时目标.可见,笔者所提预编码设计方案在时延性能优化上能满足更低的时延要求.
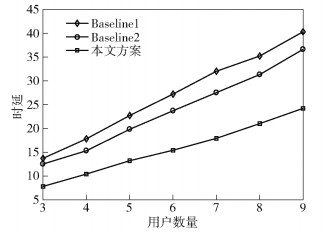
|
图 5 系统时延与用户数量关系 |
综合图 2~图 5可得,通过调整李雅普诺夫控制参数,本文方案对长期平均功耗和长期平均时延联合优化,可以达到一个折中的效果.相比于其他2个方案,本文方案综合考虑信道和队列状态的马尔可夫特性,以长期平均性能为优化目标,在时延和功耗性能优化中,能达到更好的优化效果.
图 6所示为系统功耗随功耗权重系数变化的关系.其中,wk+wM=1.由图可知,随着MEC服务器端功耗权重系数增加,MEC服务器端功耗持续减小,用户端功耗随之增加,同时系统加权总功耗随系数先增后减.这是因为优化目标函数中采用了最小加权功耗,随wM的增大,MEC服务器端的功耗逐渐成为主要优化目标,造成卸载减少,MEC服务器端功耗降低.因此,通过设置合适的功耗权重系数可以均衡系统对MEC服务器端与用户端的功耗.
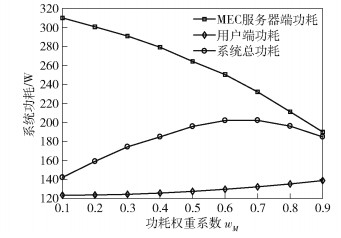
|
图 6 系统功耗与MEC服务器端功耗权重系数关系 |
针对多用户-多移动边缘计算服务器系统进行优化,综合考虑时延、功耗等因素,以降低系统的平均开销为目标,利用李雅普诺夫优化方法对系统的综合性能进行优化.仿真结果表明,相比于其他2个方案,通过预编码设计优化的方案能满足更低的功耗和时延要求.
| [1] |
Blanco B, Fajardo J O, Giannoulakis I, et al. Technology pillars in the architecture of future 5G mobile networks:NFV, MEC and SDN[J]. Computer Standards & Interfaces, 2017, 54(4): 216-228. |
| [2] |
Wang Chenmeng, Yu F R, Liang Chengchao, et al. Joint computation offloading and interference management in wireless cellular networks with mobile edge computing[J]. IEEE Transactions on Vehicular Technology, 2017, 66(8): 7432-7445. DOI:10.1109/TVT.2017.2672701 |
| [3] |
Xu Jie, Sun Yuxuan, Chen Lixing, et al.E2M2: energy efficient mobility management in dense small cells with mobile edge computing[C]//IEEE International Conference on Communications(ICC).New York: IEEE Press, 2017: 17065927.
|
| [4] |
Han Kaifeng, Ko S W, Huang Kaibin.Spatial modeling and latency analysis for mobile edge computing in wireless networks[C]//IEEE International Conference on Communications (ICC).New York: IEEE Press, 2018: 17971408.
|
| [5] |
Cheng Kang, Teng Yinglei, Sun Weiqi, et al.Energy-efficient joint offloading and wireless resource allocation strategy in multi-MEC server systems[C]//IEEE International Conference on Communications (ICC).New York: IEEE Press, 2018: 8422877.
|
| [6] |
Wang Wei, Lau V K N, Peng Mugen. Delay-aware uplink Fronthaul allocation in cloud radio access networks[J]. IEEE Transactions on Wireless Communications, 2017, 16(7): 4275-4287. DOI:10.1109/TWC.2017.2696000 |
| [7] |
Li Jian, Wu Jingxian, Peng Mugen, et al.Queue-aware joint Remote radio head activation and beamforming for green cloud radio access networks[C]//IEEE Global Communications Conference.New York: IEEE Press, 2015: 15808266.
|
| [8] |
Chen M H, Liang Ben, Dong Min.Joint offloading decision and resource allocation for multi-user multi-task mobile cloud[C]//IEEE International Conference on Communications(ICC).New York: IEEE Press, 2016: 16141619.
|
| [9] |
Wu Xiaoxiao, So A, Pan Jiaxian, et al. Semidefinite relaxation and approximation analysis of a beamformed alamouti scheme for relay beamforming networks[J]. IEEE Transactions on Signal Processing, 2017, 65(9): 2428-2443. DOI:10.1109/TSP.2016.2633245 |


