针对广义频分复用(GFDM)在频率选择性信道下的最小均方误差(MMSE)接收机计算复杂度过高的问题,提出了一种基于矩阵解构的低复杂度GFDM系统的MMSE接收机解调算法.该方法对涉及的大尺寸矩阵做分块处理,发掘了矩阵的特殊性质(稀疏性、准三对角性和块对称性等),进而将一系列大矩阵的相乘和求逆运算转化为相应子块间的相乘和求逆,从而使得其耗费的复数乘法次数比原始的MMSE接收机解调算法低2~3个数量级.仿真结果表明,所提出的接收机不会导致误比特率性能下降,因而在未来移动通信的解调系统中具有较高的应用价值.
Aiming at the problem that the computation complexity of the existing minimum mean square error (MMSE) demodulator with generalized frequency division multiplexing (GFDM) over frequency selective channel is relatively high, a matrix deconstruction based low-complexity MMSE GFDM receiver is proposed. By utilization of the particular structures (sparse, quasi-tridiagonal, block-symmetric, etc.) in a series of large-sized matrices involved in the receiver, either of large-sized matrix manipulations (including matrix multiplication and matrix inversion) is partitioned into small-sized matrix manipulations, thereby considerably reducing the computational complexity. Quantitively speaking, the times of complex multiplications consumed by the proposed MMSE receiver is 2-3 amount levels lower than the original MMSE receiver. Moreover, simulation shows that the proposed receiver does not suffer from any bit-error-rate degradation. Therefore, the proposed MMSE GFDM receiver possesses vast potentials for future 5G demodulation applications.
未来移动通信面临着诸多挑战,如在机器通信(MTC,machine type communication)[1]、触觉互联网[2]中,需要实现大数据的迸发式传输,在物联网(the Internet of thing)[3]和车载通信(V2V,vehicle-to-vehicle)[4]中,需要以较低的时延传输信息等.然而,正交频分复用(OFDM,orthogonal frequency division multiplexing)作为当前无线通信中主流的调制方式,因其存在循环前缀占据时间长、对频偏敏感、带外辐射大、子载波利用率不高等缺陷[5-6],难以适应上述挑战.相比较而言,Fettweis等[7]提出的广义频分复用(GFDM,generalized frequency division multiplexing)调制技术可以克服OFDM的这些缺陷.作为一种更高效的多载波调制技术,1个GFDM符号允许包含多个子载波和子符号,因而可适应大数据的迸发传输需求;而且在GFDM块中,多个子符号仅需插入一个CP,故省去了OFDM中单个子符号插入CP的时间损耗,减小了延时;另外,GFDM将数字滤波器引入多载波调制中,相比于OFDM大大降低了带外辐射.因此,近年来GFDM已成为国际上较为认可的第5代移动通信系统(5G,the fifth generation of mobile communications)的物理层调制备选方案.
相比于OFDM,GFDM在发送端的调制优势是以增大接收端的解调复杂度为代价的. GFDM的解调方式共有3种[8-9]:匹配滤波(MF,matched filter)接收、迫零(ZF,zero forcing)接收和最小均方误差(MMSE,minimum mean square error)接收. Michailow等[10]指出,相比于其他两种方式,MMSE接收机可权衡消除自干扰和抑制噪声2个方面,而且自身就包含了信道均衡和信号解调的过程,因而是实用价值更高的GFDM解调方式.
由于GFDM解调算法中往往包含信道均衡过程,其计算复杂度与信道冲激响应密切相关.然而现有的低复杂度MMSE接收机设计方案(基于Gabor变换的接收机[11]和两步骤的MMSE接收机[8])只考虑了最理想的加性高斯白噪声(AWGN,additive white Gaussian noise)信道情况,而无线信道不可避免地会存在多径效应和各类衰落[12],相比于AWGN,频率选择性信道(FSC,frequency selective channel)[13]模型更适于反映这些实际情况,因而迫切需要研发出适于FSC信道传输的低复杂度GFDM解调方案.
笔者提出了一种基于矩阵解构的低复杂度MMSE接收机解调算法.通过剖析MMSE接收机理论表达式中各特殊矩阵结构(稀疏、重复、准三对角或块对称),对其涉及的矩阵相乘、求逆等运算做了数学上的等效简化处理,实现了低复杂度的解调设计.数值仿真结果表明,该数学等效性可保证所设计的MMSE接收机相比于原有接收机不会使误比特率(BER,bit error rate)性能下降,其解调的计算复杂度比原始MMSE接收机低2~3个数量级.因此,笔者提出的解调算法具有较高的应用价值.
1 GFDM系统模型 1.1 发射机模型对于1个GFDM符号,其时域发送信号为
| $ \begin{array}{l} x\left( n \right) = \sum\limits_{k = 0}^{K - 1} {{x_k}\left( n \right) = } \\ {\sum\limits_{k = 0}^{K - 1} {\sum\limits_{m = 0}^{M - 1} {{d_k}\left( m \right)g\left[ {\left( {n - mK} \right)\bmod \;N} \right]} }\;{\rm{e}} ^{{\rm{j}}\frac{{2{\rm{ \mathit{ π} }}}}{K}kn}},\\ \mathit{n = }{\rm{0,1,\cdot\cdot\cdot,}}\;\mathit{N} - {\rm{1}} \end{array} $ | (1) |
其中:K为子载波数;M为子符号数;g=[g(0), …, g(N-1)]T为原型数字滤波器;N=KM为输入序列d的长度,序列d可分成K个长度为M的分段,d=[d0T, d1T, …, dK-1T],dk=[dk(0), …, dk(M-1)]T.从而,式(1)x=[x(0), …, x(N-1)]T的矩阵形式表示为
| $ \mathit{\boldsymbol{x = Ad}} $ | (2) |
其中:A为KM×KM的发送矩阵,其结构为
| $ \mathit{\boldsymbol{A = }}\left[ {{\mathit{\boldsymbol{\varepsilon }}_0}\mathit{\boldsymbol{G}}{\rm{,}}{\mathit{\boldsymbol{\varepsilon }}_1}\mathit{\boldsymbol{G}}{\rm{,\cdot\cdot\cdot,}}{\mathit{\boldsymbol{\varepsilon }}_{K - 1}}\mathit{\boldsymbol{G}}} \right] $ | (3) |
其中:εk=diag[1, ej2πk/K, …, ej2πk(N-1)/K]为与第k个子载波对应的KM×KM调制矩阵,G为KM×M的滤波矩阵,其结构为
| $ \mathit{\boldsymbol{G = }}\left[ {{\mathit{\boldsymbol{g}}_{\rm{0}}},{\rm{\cdot\cdot\cdot,}}{\mathit{\boldsymbol{g}}_\mathit{m}},{\rm{\cdot\cdot\cdot}},{\mathit{\boldsymbol{g}}_{\mathit{M - 1}}}} \right] $ | (4) |
其中:gm=[gm(0), …, gm(N-1)]T为原型数字滤波器g做mK位的循环移位结果(m=0, …, M-1),即
| $ {g_m}\left( n \right) = g\left[ {\left( {n - mK} \right)\bmod \;N} \right],n = 0,1,{\rm{\cdot\cdot\cdot}},N - 1 $ | (5) |
假定FSC的冲激响应为h=[h0, h1, …, hNch-1]T,Nch为信道长度. Renfors等[8]指出,发射序列x经过插入循环前缀、信道传输、去除循环前缀后,其接收信号r可描述为
| $ \mathit{\boldsymbol{r = x}} \circledast \mathit{\boldsymbol{\tilde h + n}} $ | (6) |
其中:
为了在消除自干扰和抑制噪声之间实现权衡,采用MMSE接收机进行GFDM系统解调.理论上,该接收机的解调信号
| $ \mathit{\boldsymbol{\hat d = }}{\left[ {\sigma _\mathit{n}^2{\boldsymbol{I}_{KM}} + {{\left( {\mathit{\boldsymbol{HA}}} \right)}^{\rm{H}}}\mathit{\boldsymbol{HA}}} \right]^{ - 1}}{\left( {\mathit{\boldsymbol{HA}}} \right)^{\rm{H}}}\mathit{\boldsymbol{r}} $ | (7) |
其中:IKM为单位矩阵,信道矩阵H为
为导出快速解调算法,不妨把式(7)的MMSE解调分解成如下的运算步骤:
| $ \left. \begin{array}{l} \mathit{\boldsymbol{B}}{\rm{ = }}{\left( {\mathit{\boldsymbol{HA}}} \right)^{\rm{H}}}\\ \mathit{\boldsymbol{ \boldsymbol{\varPhi} = }}\sigma _\mathit{n}^2{\boldsymbol{I}_{KM}} + \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{B}}^{\rm{H}}}\\ \mathit{\pmb{\Psi = }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{ - 1}}\\ \mathit{\boldsymbol{q = Br}}\\ \mathit{\boldsymbol{\hat d = \boldsymbol{\varPsi} q}} \end{array} \right\} $ | (8) |
式(8)的计算量主要集中在3个方面:1)计算B矩阵;2)计算BBH矩阵;3)计算矩阵Φ的逆矩阵.随着子载波数K和子符号数M的增加,这3方面的乘法计算量均急剧攀升,因而需根本上降低其复杂度.
2 低复杂度的MMSE接收机利用矩阵H、A、Φ及其逆矩阵Ψ=Φ-1具有的某些特殊结构(稀疏、重复、准三对角或块对称)来降低接收机的复杂度.
2.1 矩阵H和A的结构由于式(4)的矩阵G是由原型数字滤波器g通过循环移位得到,故式(3)发送矩阵A中第k个子载波εkG的所有M列元素相同.从而矩阵HA的KM列中,只有K列是互相独立的,其余KM-K列可以由这K列做循环移位得到.此外,由于H是由
故矩阵乘法HA涉及的计算量可降为其直接实现计算量的
因为式(7)中的σn2IKM是一个单元素对角阵,所以矩阵Φ和矩阵(HA)HHA具有相同的结构.不妨将KM×KM矩阵Φ分成K2个子块,如
| $ \mathit{\boldsymbol{ \boldsymbol{\varPhi} = }}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{0,0}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{0,1}}}& \ldots &{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{0,K - 1}}}\\ {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{1,0}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{1,1}}}& \ldots &{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{1,K - 1}}}\\ \vdots&\vdots &\;& \vdots \\ {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{K - 1,0}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{K - 1,1}}}& \ldots &{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{K{\rm{ - }}1,K - 1}}} \end{array}} \right] $ | (9) |
其中Φi, j(i, j=0, 1, …, K-1)为M×M的矩阵.
式(3)两边同时左乘信道矩阵H,有
| $ \mathit{\boldsymbol{HA = }}\left[ {\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{\varepsilon }}_{\rm{0}}}\mathit{\boldsymbol{G,H}}{\mathit{\boldsymbol{\varepsilon }}_1}\mathit{\boldsymbol{G,}}{\rm{\cdot\cdot\cdot}}\mathit{\boldsymbol{,H}}{\mathit{\boldsymbol{\varepsilon }}_{{{\mathit{K} - 1}}}}\mathit{\boldsymbol{G}}} \right] $ | (10) |
结合式(8)~式(10),可得到
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{i,j}}} = \left\{ \begin{array}{l} {\left( {\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{\varepsilon }}_\mathit{i}}\mathit{\boldsymbol{G}}} \right)^{\rm{H}}}\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{\varepsilon }}_j}\mathit{\boldsymbol{G + }}\sigma _n^2{\mathit{\boldsymbol{I}}_{KM}},\;\;\;i = j\\ {\left( {\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{\varepsilon }}_\mathit{i}}\mathit{\boldsymbol{G}}} \right)^{\rm{H}}}\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{\varepsilon }}_j}\mathit{\boldsymbol{G}},\;\;i \ne j \end{array} \right. $ | (11) |
下面证明矩阵Φ的3个关于各分块之间的性质:准三对角矩阵、关于主对角线对称和关于反次对角线共轭对称.
2.2.1 准三对角矩阵需指出,式(4)矩阵G中的每个gm都是原型数字滤波器g的时域循环移位版本,故都具有低通传输特性.此外,对于式(3)中的εiG操作,其调制矩阵εi的作用是把该低通传输曲线搬移到相应的频段ω∈[(i-0.5)2π/K, (i+0.5)2π/K],如图 1所示.
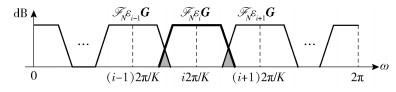
|
图 1 调制后各子载波的频谱分布示意图 |
图 1中,各子载波占有带宽均为Δω=2π/K,所以εiG的频谱只会与其相邻两侧的频谱(εi-1G和εi+1G)重叠.此外,对于2个不同的子载波εiG和εjG,如果其间隔大于Δω(|i-j|=2, 3, …, K-2),相互干扰可忽略,即
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{i,j}}} = {\left( {\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{\varepsilon }}_\mathit{i}}\mathit{\boldsymbol{G}}} \right)^{\rm{H}}}\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{\varepsilon }}_j}\mathit{\boldsymbol{G}} \buildrel\textstyle.\over= 0 $ | (12) |
结合式(9)、式(11)和式(12)可推得,矩阵Φ中除了3条对角线和矩阵2个角上共3K个子块,其余子块均为零矩阵,故称这种矩阵为准三对角矩阵.
2.2.2 关于主对角线对称矩阵从式(11)可推知,矩阵Φ是一个Hermitian矩阵,即
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{i,j}}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{^{j,i}}^{\rm{H}} $ | (13) |
因此,矩阵Φ中关于对角线对称的子块满足:
| $ \left. \begin{array}{l} {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{i,j - }{\rm{1}}}}{\rm{ = }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{i}{\rm{ - 1}}\mathit{,i}}^{\rm{H}}},i = 1,{\rm{\cdot\cdot\cdot}},\mathit{K} - {\rm{1}}\\ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{0}}\mathit{,K - }{\rm{1}}}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{K - 1,0}^{\rm{H}} \end{array} \right\} $ | (14) |
从而联立式(11)、式(14),有
| $ \left. \begin{array}{l} {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{i,j - }{\rm{1}}}}{\rm{ = }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{i}{\rm{ - 1}}\mathit{,i}}},i = 1,{\rm{\cdot\cdot\cdot}},\mathit{K} - {\rm{1}}\\ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{0}}\mathit{,K - }{\rm{1}}}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{K - 1,0}} \end{array} \right\} $ | (15) |
式(15)表明,Φ是一个关于对角线的块对称矩阵.
2.2.3 关于反次对角线共轭对称矩阵从调制矩阵的定义εk=diag[1, ej2πk/K, …, ej2πk(N-1)/K]易知
| $ {\mathit{\boldsymbol{\varepsilon }}_\mathit{i}} = {\boldsymbol{{\bar \varepsilon }}_{K{\rm{ - }}\mathit{i}}} $ | (16) |
其中
令j分别等于i、i-1和i+1,并结合式(16)、式(11)、式(12)有
| $ \left. \begin{array}{l} {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{i,i}}} = {{\mathit{\boldsymbol{ \boldsymbol{\bar \varPhi} }}}_{\mathit{K - i,K - i}}}\\ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{i,i - }{\rm{1}}}} = {{\mathit{\boldsymbol{ \boldsymbol{\bar \varPhi} }}}_{\mathit{K - i,K - }\left( {i - 1} \right)}} = {{\mathit{\boldsymbol{ \boldsymbol{\bar \varPhi} }}}_{\mathit{K - }\left( {i - 1} \right)\mathit{,K - i}}}\\ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{i,i + }{\rm{1}}}}{\rm{ = }}{{\mathit{\boldsymbol{ \boldsymbol{\bar \varPhi} }}}_{\mathit{K - i,K - }\left( {i + 1} \right)}} = {{\mathit{\boldsymbol{ \boldsymbol{\bar \varPhi} }}}_{\mathit{K - }\left( {i + 1} \right)\mathit{,K - i}}} \end{array} \right\} $ | (17) |
对于矩阵Φ位于2个角上的子块Φ0, K-1和ΦK-1, 0,把i=K-1和j=0代入式(17)中的第3个式子,并结合式(15)可得
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{K - }{\rm{1}}\mathit{,}{\rm{0}}}}{\rm{ = }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{0}}\mathit{,K - }{\rm{1}}}} = {{\mathit{\boldsymbol{ \boldsymbol{\bar \varPhi} }}}_{{\rm{0,1}}}} = {{\mathit{\boldsymbol{ \boldsymbol{\bar \varPhi} }}}_{{\rm{0,1}}}} $ | (18) |
式(17)、式(18)表明,矩阵Φ关于反次对角线共轭对称.
基于以上3个性质,矩阵Φ可表示为
| $ \mathit{\boldsymbol{ \boldsymbol{\varPhi} = }}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{0,0}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{1,0}}}&\mathbf{0}& \cdots &\mathbf{0}&{{{\mathit{\boldsymbol{ \boldsymbol{\bar \varPhi} }}}_{{\rm{1,0}}}}}\\ {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{1,0}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{1,1}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{2,1}}}&\mathbf{0}& \cdots &\mathbf{0}\\ \mathbf{0}&{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{2,1}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{2,2}}}& \ddots&\ddots&\vdots \\ \vdots &\mathbf{0}& \ddots&\ddots&\ddots &\mathbf{0}\\ \mathbf{0}& \vdots&\ddots&\ddots &{{{\mathit{\boldsymbol{ \boldsymbol{\bar \varPhi} }}}_{2,2}}}&{{{\mathit{\boldsymbol{ \boldsymbol{\bar \varPhi} }}}_{2,1}}}\\ {{{\mathit{\boldsymbol{ \boldsymbol{\bar \varPhi} }}}_{1,0}}}&\mathbf{0}& \cdots &\mathbf{0}&{{{\mathit{\boldsymbol{ \boldsymbol{\bar \varPhi} }}}_{2,1}}}&{{{\mathit{\boldsymbol{ \boldsymbol{\bar \varPhi} }}}_{1,1}}} \end{array}} \right] $ | (19) |
Charmonman[14]指出,当原矩阵是准三对角阵,其逆矩阵具有与原矩阵相同的对称性.故若把KM×KM逆矩阵Ψ同样分成与原矩阵Φ类似的K2个M×M的子块,则Ψ也具有关于主对角线和反次对角线的共轭对称性,从而矩阵Ψ的结构可表示为
| $ {\mathit{\pmb{\Psi }}_{\mathit{i,j}}} = \left\{ \begin{array}{l} {\mathit{\pmb{\Psi }}_{\mathit{i,j}}},\;i \ge j,i + j \le K\\ {\mathit{\pmb{\Psi }}_{\mathit{j,i}}},\;i < j,i,j \in \left[ {0,K - 1} \right]\\ {{\mathit{\pmb{\bar \Psi }}}_{k - j,K - i}},\;i \ge j,i + j > K \end{array} \right. $ | (20) |
利用2.2节所分析的矩阵Φ的3个性质,可把KM×KM的矩阵求逆Ψ=Φ-1转化成一系列M×M矩阵的求逆问题,从而显著降低复杂度.
具体地,把矩阵Φ所有K行分别与矩阵Ψ的第j列[Ψ0, j, Ψ1, j, …, ΨK-1, j]T(j=0, …, K-1)相乘,可获得以下K个方程组E0, …, EK-1:
| $ \begin{array}{c} {E_0}\left\{ \begin{array}{l} {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{0,0}}}}{\mathit{\pmb{\Psi }}_{{\rm{0,0}}}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{1,0}}}}{\mathit{\pmb{\Psi }}_{{\rm{1,0}}}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{K}{\rm{ - 1,0}}}}{\mathit{\pmb{\Psi }}_{\mathit{K}{\rm{ - 1,0}}}}{\rm{ = }}{\mathit{\boldsymbol{I}}_\mathit{M}}\\ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{1,0}}}}{\mathit{\pmb{\Psi }}_{{\rm{0,0}}}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{1,1}}}}{\mathit{\pmb{\Psi }}_{{\rm{1,0}}}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{2,1}}}}{\mathit{\pmb{\Psi }}_{{\rm{2,0}}}}{\rm{ = \mathbf{0}}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{K - }{\rm{1,0}}}}{\mathit{\pmb{\Psi }}_{{\rm{0,0}}}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{K - }{\rm{1,}}\mathit{K - }{\rm{2}}}}{\mathit{\pmb{\Psi }}_{\mathit{K - }{\rm{2,0}}}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{K}{\rm{ - 1,}}\mathit{K}{\rm{ - 1}}}}{\mathit{\pmb{\Psi }}_{\mathit{K}{\rm{ - 2,0}}}}{\rm{ = \mathbf{0}}} \end{array} \right.\\ {E_{\rm{1}}}\left\{ \begin{array}{l} {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{0,0}}}}{\mathit{\pmb{\Psi }}_{{\rm{0,1}}}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{1,0}}}}{\mathit{\pmb{\Psi }}_{{\rm{1,1}}}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{K}{\rm{ - 1,0}}}}{\mathit{\pmb{\Psi }}_{\mathit{K}{\rm{ - 1,1}}}}{\rm{ = \mathbf{0}}}\\ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{1,0}}}}{\mathit{\pmb{\Psi }}_{{\rm{0,1}}}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{1,1}}}}{\mathit{\pmb{\Psi }}_{{\rm{1,1}}}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{2,1}}}}{\mathit{\pmb{\Psi }}_{{\rm{2,1}}}}{\rm{ = }}{\mathit{\boldsymbol{I}}_\mathit{M}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{K - }{\rm{1,0}}}}{\mathit{\pmb{\Psi }}_{{\rm{0,1}}}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{K - }{\rm{1,}}\mathit{K - }{\rm{2}}}}{\mathit{\pmb{\Psi }}_{\mathit{K - }{\rm{2,1}}}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{K}{\rm{ - 1,}}\mathit{K}{\rm{ - 1}}}}{\mathit{\pmb{\Psi }}_{\mathit{K}{\rm{ - 2,1}}}}{\rm{ = \mathbf{0}}} \end{array} \right.\\ \vdots \\ {E_{\mathit{K}{\rm{ - 1}}}}\left\{ \begin{array}{l} {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{0,0}}}}{\mathit{\pmb{\Psi }}_{{\rm{0,}}\mathit{K}{\rm{ - 1}}}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{1,0}}}}{\mathit{\pmb{\Psi }}_{{\rm{1,}}\mathit{K}{\rm{ - 1}}}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{K}{\rm{ - 1,0}}}}{\mathit{\pmb{\Psi }}_{\mathit{K}{\rm{ - 1,}}\mathit{K}{\rm{ - 1}}}}{\rm{ = \mathbf{0}}}\\ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{1,0}}}}{\mathit{\pmb{\Psi }}_{{\rm{0,}}\mathit{K}{\rm{ - 1}}}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{1,1}}}}{\mathit{\pmb{\Psi }}_{{\rm{1,}}\mathit{K}{\rm{ - 1}}}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{2,1}}}}{\mathit{\pmb{\Psi }}_{{\rm{2,}}\mathit{K}{\rm{ - 1}}}}{\rm{ = \mathbf{0}}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{K - }{\rm{1,0}}}}{\mathit{\pmb{\Psi }}_{{\rm{0,}}\mathit{K}{\rm{ - 1}}}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{K - }{\rm{1,}}\mathit{K - }{\rm{2}}}}{\mathit{\pmb{\Psi }}_{\mathit{K - }{\rm{2,}}\mathit{K}{\rm{ - 1}}}} + \\ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{K}{\rm{ - 1,}}\mathit{K}{\rm{ - 1}}}}{\mathit{\pmb{\Psi }}_{\mathit{K}{\rm{ - 1,}}\mathit{K}{\rm{ - 1}}}}{\rm{ = }}{\mathit{\boldsymbol{I}}_\mathit{M}} \end{array} \right. \end{array} $ | (21) |
其中IM为M×M的单位阵.
利用矩阵Ψ的块对称性质,Ψ=Φ-1只需求解式(21)的前K/2+1个方程(Ej, j=0, …, K/2),可根据列标号j分3种情况:① j=0时,求解子块Ψ0, 0, Ψ1, 0, …, ΨK-1, 0;② 1≤j≤K/2-1时,求解子块Ψi, j, i=j, …, K-j; ③ j=K/2时,求解子块ΨK/2, K/2.
1) 情况1. j=0时,求解子块Ψ0, 0, Ψ1, 0, …, ΨK-1, 0共K个子块.
对于方程组E0,可从其最后一行开始,推出ΨK-1, 0为
| $ \begin{array}{l} {\mathit{\pmb{\Psi }}_{\mathit{K}{\rm{ - 1,0}}}} = \\ - {\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{K - }{\rm{1,}}\mathit{K - }{\rm{1}}}} - {\mathit{\boldsymbol{X}}_{\mathit{K - }{\rm{1}}}}} \right)^{ - 1}}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{K - }{\rm{1,}}\mathit{{K}- 2 }}} - {\mathit{\pmb{\Psi }}_{\mathit{K - }{\rm{2,0}}}} - {\mathit{\boldsymbol{Y}}_{\mathit{K}{\rm{ - 1}}}}{\mathit{\pmb{\Psi }}_{{\rm{0,0}}}}} \right) \end{array} $ | (22) |
其中:XK-1=0,YK-1=-ΦK-1, 0.进而把式(22)代入E0倒数第2行可求解出ΨK-2, 0, 再以此类推,逐次把下行计算出的ΨK-i+1, 0代入上一行计算出ΨK-i, 0,可归纳出ΨK-i, 0解析式为
| $ \begin{array}{l} {\kern 1pt} {\mathit{\pmb{\Psi }}_{\mathit{i}{\rm{,0}}}} = \\ \left\{ \begin{array}{l} {\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{0,0}}}} - {\mathit{\boldsymbol{X}}_{\rm{0}}} - {\mathit{\boldsymbol{Y}}_{\rm{0}}} + {\mathit{\boldsymbol{Z}}_{\mathit{K - }{\rm{1}}}}} \right)^{ - 1}},\;i = 0\\ - {\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{i}{\rm{,}}\mathit{i}}} - {\mathit{\boldsymbol{X}}_\mathit{i}}} \right)^{ - 1}}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{i}{\rm{,}}\mathit{i - }{\rm{1}}}}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{\mathit{i}{\rm{ - 1,0}}}} - {\mathit{\boldsymbol{Y}}_\mathit{i}}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{{\rm{0,0}}}},\;1 \le i \le K - 1} \right) \end{array} \right. \end{array} $ | (23) |
其中
| $ \begin{array}{l} {\mathit{\boldsymbol{X}}_{\mathit{K - i}}} = \\ \left\{ \begin{array}{l} 0,\;i = 1\\ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{K - i + }{\rm{1,}}\mathit{K - }{\rm{1}}}}{\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{K - i + }{\rm{1,}}\mathit{K - i + }{\rm{1}}}} - {\mathit{\boldsymbol{X}}_{\mathit{K - i + }{\rm{1}}}}} \right)^{ - 1}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{K - i + }{\rm{1,}}\mathit{K - i}}},\;2 \le i \le K \end{array} \right. \end{array} $ | (24) |
| $ \begin{array}{c} \;{\mathit{\boldsymbol{Y}}_{\mathit{K - i}}} = \\ \left\{ \begin{array}{l} \mathit{\boldsymbol{ - }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{K - }{\rm{1,0}}}},\;i = 1\\ \mathit{\boldsymbol{ - }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{K - i + }{\rm{1,}}\mathit{K - }{\rm{1}}}}{\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{K - i + }{\rm{1,}}\mathit{K - i + }{\rm{1}}}} - {\mathit{\boldsymbol{X}}_{\mathit{K - i + }{\rm{1}}}}} \right)^{ - 1}}{\mathit{\boldsymbol{Y}}_{\mathit{K - i + }{\rm{1}}}},\;2 \le i \le K \end{array} \right. \end{array} $ | (25) |
| $ {\mathit{\boldsymbol{Z}}_\mathit{i}} = \left\{ \begin{array}{l} {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{1,0}}}},\;i = 0\\ - {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{i}{\rm{ + 1,}}\mathit{i}}}{\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{i}{\rm{,}}\mathit{i}}}{\rm{ - }}{\mathit{\boldsymbol{X}}_\mathit{i}}} \right)^{ - 1}}\left( {{\mathit{\boldsymbol{Z}}_{\mathit{i - }{\rm{1}}}} + {\mathit{\boldsymbol{Y}}_\mathit{i}}} \right),\;1 \le i \le K - 2\\ - {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{K - }{\rm{1,0}}}}{\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{i}{\rm{,}}\mathit{i}}}{\rm{ - }}{\mathit{\boldsymbol{X}}_\mathit{i}}} \right)^{ - 1}}\left( {{\mathit{\boldsymbol{Z}}_{\mathit{i - }{\rm{1}}}} + {\mathit{\boldsymbol{Y}}_\mathit{i}}} \right),\;i{\rm{ = }}K - {\rm{1}} \end{array} \right. $ | (26) |
从式(21)~式(26)可看出,根据给定矩阵Φ内的各子块,可算出辅助子块X0~XK-1、Y0~YK-1、Z0~ZK-1, 进而代入通式(23),依次以嵌套方式分别求解出子块Ψ0, 0, …, ΨK-1, 0.
2) 情况2. 1≤j≤K/2-1时,求解子块Ψi, j, i=j, …, K-j共K2/4-1个子块.
不妨把式(21)的方程组Ej写为
| $ \left. \begin{array}{l} {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{0,0}}}}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{{\rm{0,}}\mathit{j}}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{1,0}}}}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{{\rm{1,}}\mathit{j}}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{K - }{\rm{1,0}}}}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{\mathit{K}{\rm{ - }}{1}{\rm{,}}\mathit{j}}}{\rm{ = }}\mathbf{0}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{j}{\rm{,}}\mathit{j - }{\rm{1}}}}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{\mathit{j - }{\rm{1,}}\mathit{j}}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{j}{\rm{,}}\mathit{j}}}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{\mathit{j}{\rm{,}}\mathit{j}}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{j } +{\rm{1,}}\mathit{j}}}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{\mathit{j } +{\rm{1,}}\mathit{j}}} = {\mathit{\boldsymbol{I}}_\mathit{M}}\\ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{j } +{\rm{1,}}\mathit{j}}}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{\mathit{j}{\rm{,}}\mathit{j}}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{j } +{\rm{1,}}\mathit{j } +{\rm{1}}}}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{\mathit{j } +{\rm{1,}}\mathit{j}}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{j } +{\rm{2,}}\mathit{j } +{\rm{1}}}}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{\mathit{j } +{\rm{2,}}\mathit{j}}} = \mathbf{0}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{K - }{\rm{1,0}}}}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{{\rm{0,}}\mathit{j}}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{K - }{\rm{1,}}\mathit{K - }{\rm{2}}}}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{\mathit{K - }{\rm{2,}}\mathit{j}}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{K - }{\rm{1,}}\mathit{K - }{\rm{1}}}}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{\mathit{K - }{\rm{1,}}\mathit{j}}} = \mathbf{0} \end{array} \right\} $ | (27) |
类似于情况1的推导,采用嵌套方法,依次把Ej的下一行各子块代入前一行,可得
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{\mathit{i}{\rm{,}}\mathit{j}}} = \\ \left\{ \begin{array}{l} - {\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{j}{\rm{,}}\mathit{j}}}{\rm{ - }}{\mathit{\boldsymbol{X}}_\mathit{j}}} \right)^{ - 1}}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{j}{\rm{,}}\mathit{j - }{\rm{1}}}}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{\mathit{j,j - }{\rm{1}}}} - {\mathit{\boldsymbol{Y}}_\mathit{j}}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{\mathit{j,}{\rm{0}}}} - {\mathit{\boldsymbol{I}}_\mathit{M}}} \right),\;\;\;i = j\\ - {\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{i}{\rm{,}}\mathit{i}}}{\rm{ - }}{\mathit{\boldsymbol{X}}_\mathit{i}}} \right)^{ - 1}}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{i}{\rm{,}}\mathit{i - }{\rm{1}}}}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{\mathit{i - }{\rm{1,}}\mathit{j}}} - {\mathit{\boldsymbol{Y}}_\mathit{i}}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{\mathit{j,}{\rm{0}}}}} \right),\;\;\;i = j + 1, \cdots ,K - j \end{array} \right. \end{array} $ | (28) |
3) 情况3.当j=K/2时,只有ΨK/2, K/2需要解.
这时,从式(21)的方程组EK/2的第K/2行方程,并根据Ψ的块对称性,可推出
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{K/2,\mathit{K/}{\rm{2}}}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{K/2,\mathit{K/}{\rm{2}}}^{ - 1}\left( {{\mathit{\boldsymbol{I}}_\mathit{M}} - {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{K/2,\mathit{K/}{\rm{2 - 1}}}}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{K/2,\mathit{K/}{\rm{2 - 1}}}} -\\ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{K/2,\mathit{K/}{\rm{2 + 1}}}}{{\mathit{\boldsymbol{ \boldsymbol{\bar \varPsi} }}}_{K/2,\mathit{K/}{\rm{2 - 1}}}}} \right) $ | (29) |
以上3种情况以“化整为零”的方式计算出矩阵Ψ内K+(K2/4-1)+1=K2/4+K个独立子块,而剩余3K2/4-K个子块可根据式(20)所示的对称性快速赋值得到,从而大大节省了计算量.
3 计算复杂度分析用复数乘法(CM,complex multiplication)次数作为算法复杂度评价指标,该复杂度可通过统计式(8)各步骤所耗费的CM次数来体现.
3.1 原始MMSE接收机所需CM次数显然,式(8)的前2步运算(B=(HA)H和Φ=σn2IKM+BBH)都涉及KM×KM的方阵乘法运算,总共消耗2(KM)3次CM.此外,由于矩阵Φ是正定对称矩阵,可利用Cholesky分解计算其逆矩阵Ψ,需要消耗(KM)3/3次CM.式(8)的后2个步骤(q=Br和
| $ C{\rm{ = }}\frac{7}{3}{\left( {KM} \right)^3} + 2\;{\left( {KM} \right)^2} $ | (30) |
对于式(8)中的步骤1,3.1节指出,相比原始方法,利用矩阵HA的特殊结构可使计算复杂度降至原始MMSE接收机的Nch/(KM2)×100%,即所需的CM为Nch/(KM2)×(KM)3=NchK2M.
对于式(8)中的步骤2,3.2节指出,由于矩阵Φ具有2个特殊性质,在K2个子块中只有K+1个子块需要计算,因此计算矩阵Φ需要消耗(K+1)/K2×(KM)3=K(K+1)M3次CM.
对于式(8)中的步骤3,为量化2.4节所详述的快速求逆运算Ψ=Φ-1的复杂度,表 1列出了求取各辅助子块和Ψ内的各子块所耗费的操作(子块乘法或子块求逆)次数.
|
|
表 1 本文MMSE接收机求逆算法的子块操作次数 |
从表 1可得,所提出的大矩阵求逆算法共需K2/4+4K-3次子块乘法和3K2/4+9K-9次子块求逆,由于每个子块尺寸为M×M,所以Ψ=Φ-1共消耗的CM次数为
| $ \begin{array}{c} \left( {{K^2}/4 + 4K - 3 + 3{K^2}/4 + 9K - 9} \right){\mathit{M}^{\rm{3}}} = \\ \left( {{K^2} + 13K - 12} \right){\mathit{M}^{\rm{3}}} \end{array} $ |
对于式(8)中的q=Br和
| $ {C_p} = {N_{{\rm{ch}}}}{K^2}M + \left( {2{K^2} + 14K - 12} \right){M^3} + 2{\left( {KM} \right)^2} $ | (31) |
根据式(30)和式(31),图 2和图 3给出原始和本文MMSE接收机的CM次数曲线对比,其中Nch为K/4. 图 2描述了不同子符号数M下的复杂度对比(子载波数K=256),图 3描述了不同子载波数K下的计算复杂度对比(子符号数M=11),
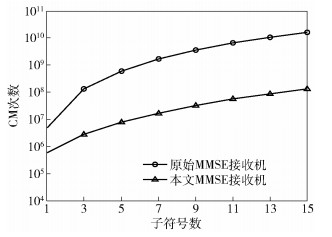
|
图 2 不同子符号数下的计算复杂度对比 |
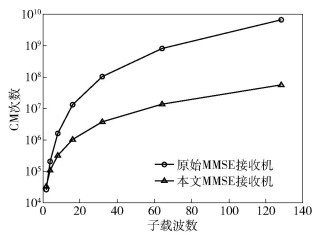
|
图 3 不同子载波数下的计算复杂度对比 |
从图 2和图 3可看出,笔者提出的MMSE接收机所需消耗的CM次数比原始MMSE接收机低2~3个数量级.这是由于在节省计算量方面,第2节所证明各矩阵的特殊对称结构和基于“化整为零”的矩阵求逆算法均发挥了决定性作用.
4 实验仿真通过实验仿真,对FSC下的原始MMSE和笔者提出的MMSE接收机之间的误比特率性能进行比较.实验设置FSC冲激响应为h(n)=10-n/(Nch-1)(n=0, …, Nch-1, Nch≤NCP)[8], 选用RRC滤波器,采用16QAM调制方式.其他参数设置如表 2所示.
|
|
表 2 实验参数设置 |
实验中取信噪比Eb/N0范围为[0, 28]dB,对于每个Eb/N0点,进行1000次Monte Carlo仿真,每次仿真使用1000个GFDM符号. 图 4给出了接收机的误比特率BER性能曲线.
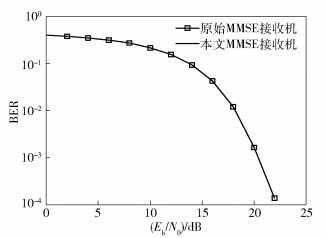
|
图 4 FSC下接收机的误比特率性能对比 |
从图 4可看出,原始和本文接收机的误比特率曲线完全一致,说明所提出的MMSE接收机不会造成误比特率性能下降,因此也证明笔者所提出的低复杂度算法与原始算法在数学上是等价的.
5 结束语针对常见的频率选择性信道,提出了基于矩阵解构的GFDM低复杂度MMSE接收机解调算法.其核心机理在于充分利用了MMSE接收机理论表达式中各矩阵的特殊结构,如稀疏、重复、准三对角或块对称.基于该特殊结构,对其涉及的矩阵相乘、求逆等运算做了数学上等效的简化处理,其数学等效性通过误比特率对比测试得到证明.
鉴于提出的高效解调算法的计算复杂度比原始MMSE接收机低2~3个数量级,该算法在未来移动通信的物理层调制应用中具有较高的参考价值.
| [1] |
Condoluci M, Dohler M, Araniti G, et al. Toward 5G DenseNets:architectural advances for effective machine-type communications over femtocells[J]. IEEE Communications Magazine, 2015, 53(1): 134-141. DOI:10.1109/MCOM.2015.7010526 |
| [2] |
Fettweis G P. The Tactile Internet:applications and challenges[J]. IEEE Vehicular Technology Magazine, 2014, 9(1): 64-70. DOI:10.1109/MVT.2013.2295069 |
| [3] |
Din S, Ahmad A, Paul A, et al. MGR:multi-parameter green reliable communication for internet of things in 5G network[J]. Journal of Parallel and Distributed Computing, 2018(118): 34-45. |
| [4] |
Nekovee M.Quantifying performance requirements of vehicle-to-vehicle communication protocols for rear-end collision avoidance[C]//Proceedings of the 2009 IEEE 69th Vehicular Technology Conference.New York: IEEE Press, 2009: 2084-2088.
|
| [5] |
Liu Xiqing, Chen H H, Wang Xiang, et al. Time domain precoding for OFDM/OFDMA systems without cyclic prefix[J]. IEEE Transactions on Vehicular Technology, 2018, 67(6): 5510-5514. DOI:10.1109/TVT.2018.2831203 |
| [6] |
Xie Zhenwei, Zhu Qi, Zhao Su. Resource allocation algorithm based on simultaneous wireless information and power transfer for OFDM relay networks[J]. KSⅡ Transactions on Internet and Information Systems, 2017, 11(12): 5943-5962. |
| [7] |
Fettweis G, Krondorf M, Bittner S.GFDM-generalized frequency division multiplexing[C]//Proceedings of the 2009 IEEE 69th Vehicular Technology Conference.New York: IEEE Press, 2009: 1383-1386.
|
| [8] |
Renfors M, Yli-Kaakinen J, Harris F J. Analysis and design of efficient and flexible fast-convolution based multirate filter banks[J]. IEEE Transactions on Signal Processing, 2014, 62(15): 3768-3783. DOI:10.1109/TSP.2014.2330331 |
| [9] |
Farhang A, Marchetti N, Doyle L E. Low-complexity modem design for GFDM[J]. IEEE Transactions on Signal Processing, 2016, 64(6): 1507-1518. DOI:10.1109/TSP.2015.2502546 |
| [10] |
Michailow N, Krone S, Lentmaier M, et al.Bit error rate performance of generalized frequency division multiplexing[C]//Proceedings of the 2012 IEEE 76th Vehicular Technology Conference.New York: IEEE Press, 2012: 13226638.
|
| [11] |
Matthe M, Mendes L L, Fettweis G. Generalized frequency division multiplexing in a Gabor transform setting[J]. IEEE Communications Letters, 2014, 18(8): 1379-1382. DOI:10.1109/LCOMM.2014.2332155 |
| [12] |
Sun Xuqing, Duan Jingyuan, Zou Yonggang, et al. Impact of multipath effects on theoretical accuracy of TOA-based indoor VLC positioning system[J]. Photonics Research, 2015, 3(6): 296-299. DOI:10.1364/PRJ.3.000296 |
| [13] |
Zhang Dan, Festag A, Fettweis G P. Performance of generalized frequency division multiplexing based physical layer in vehicular communications[J]. IEEE Transactions on Vehicular Technology, 2017, 66(11): 9809-9824. DOI:10.1109/TVT.2017.2723729 |
| [14] |
Charmonman S. An efficient algorithm for inverting a block-symmetric matrix[J]. Mathematics of Computation, 1967, 21(100): 715-717. DOI:10.1090/S0025-5718-67-99906-1 |


