作为第5代移动通信系统候选多址技术之一，稀疏码多址接入(SCMA, sparse code multiple access)^[1]以其优异的性能成为极具竞争力的方案^[2-3]. SCMA的主要研究对象包括码本设计与多用户检测.对于码本设计，Taherzadeh等^[4]率先提出了对选取的多维星座进行特定的星座运算进而得到用户码本的方案.这种方案通过笛卡儿积获得多维星座，其实现复杂度高，且难以推广到更高维度.作为一种改进，Cai等^[5]通过旋转和交织正交振幅调制(QAM, quadrature amplitude modulation)星座的某一子集来设计多维星座，再旋转并稀疏映射该多维星座就获得了用户码本；Yu等^[6]基于一种星形QAM，通过星座运算得到了用户码本；Bao等^[7]提出了一种利用球形编码构造多维星座进而获得用户码本的方案，该方案构造的多维星座因具有较低的峰值平均功率比(PAPR, peak to average power ratio)而使用户码本具有较好的性能.上述以Taherzadeh等^[4]为代表的典型SCMA码本设计方案主要包括对多维星座的设计和星座运算的确定.由于多维星座的设计可以归结为一类难解的非凸二次约束二次规划问题^[8]，且给定多维星座后星座运算的确定又对用户码本的性能有着重要的影响^[9]，因此，在以Taherzadeh等^[4]为代表的码本设计方案中，设计多维星座的复杂度和确定最优星座运算的难度实际上增加了码本设计的难度.

对于多用户检测，SCMA采用消息传递算法(MPA, message passing algorithm)^[10-11]. Beek等^[12]将无噪声干扰的理想接收向量之间欧氏距离的集合定义为距离谱，以优化距离谱为准则得到了性能较好的低密度扩频序列.受其启发，笔者将距离谱分析运用到SCMA码本设计上，提出了一种基于距离谱的码本设计方案.将码本的设计过程转化为简单的参数选择过程，避免了设计多维星座和确定最优星座运算的难度，并且以不影响码本唯一可译码性的方式降低了参数选择复杂度.通过采用交织降低PAPR的方式和运用所提最大化距离谱最小元素的码本设计准则，所提方案最终以较低的复杂度获得了性能优异的SCMA码本.

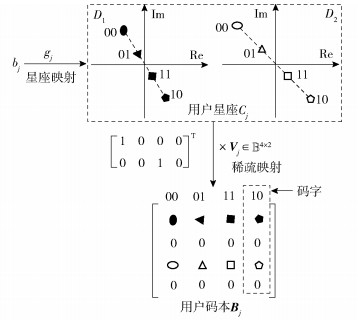
1 SCMA系统与距离谱 1.1 SCMA编译码原理

SCMA编码原理可以描述为：x_j=V_jg_j(b_j)^[4].其中：映射函数g_j将用户j的数据比特b_j∈$\mathbb{B} $^lbM×1映射为N维用户星座C_j中的星座点c_j，稀疏矩阵V_j∈$\mathbb{B} $^K×N简单地将N维复数星座点c_j映射为含有K－N个0元素的K维稀疏复数向量，即码字x_j，M个不同的码字组成了用户j的码本B_j∈$\mathbb{B} $^K×M. (N, K, M)=(2, 4, 4)时，SCMA编码原理简化示意图如图 1所示.图中：D₁和D₂为C_j的2个维度.

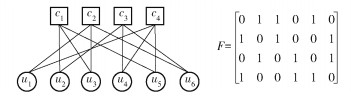
在SCMA系统中，J个用户共享K个正交资源块传输数据.各用户对资源块的占用情况可以使用因子图及其矩阵F∈$\mathbb{B} $^K×J表示.当且仅当用户节点u_j和资源节点c_k相连时，矩阵F第k行、第j列的元素F_{k, j}=1且用户j占用第k个资源块.定义ξ_k和ζ_j分别为占用第k个资源块的用户集合和用户j占用的资源块集合. (J, K)=(6, 4)时，一种因子图及其矩阵F如图 2所示.

假设J个用户时间完全同步，在上行链路基站处的接收信号为

$ \mathit{\boldsymbol{y}} = \sum\limits_{j = 1}^J {{\rm{diag}}} \left( {{\mathit{\boldsymbol{h}}_\mathit{j}}} \right){\mathit{\boldsymbol{x}}_\mathit{j}} + {\boldsymbol{n}} $

(1)

其中：n~CN(0, σ²I_K)为噪声向量，σ²为噪声功率，I_K为K维单位矩阵，y=[y₁, y₂, …, y_K]^T为接收信号向量，x_j=[x_{1, j}, x_{2, j}, …, x_{K, j}]^T为用户j的发送码字，h_j=[h_{1, j}, h_{2, j}, …, h_{K, j}]^T为用户j的信道向量.

给定接收信号y，且假定基站已知各用户的码本和信道状态，则可通过MPA以迭代的方式进行多用户检测.第t次迭代中，MPA首先更新全部资源节点到用户节点的消息M_k→j^t(x_j)，然后同时更新所有用户节点到资源节点的消息I_j→k^t(x_j)，分别可以表示为

$ M_{k \to j}^t\left( {{\mathit{\boldsymbol{x}}_\mathit{j}}} \right) = \sum\limits_{\sim {\mathit{\boldsymbol{x}}_\mathit{j}}} {\left( {{M_k}\left( \mathit{\boldsymbol{x}} \right)\prod\limits_{l \in {\xi _k}/\left\{ j \right\}} {I_{l \to k}^{t - 1}\left( {{\mathit{\boldsymbol{x}}_\mathit{j}}} \right)} } \right)} $

(2)

$ I_{j \to k}^t\left( {{\mathit{\boldsymbol{x}}_\mathit{j}}} \right) = \prod\limits_{m \in {\xi _j}/\left\{ k \right\}} {M_{m \to j}^t\left( {{\mathit{\boldsymbol{x}}_\mathit{j}}} \right)} $

(3)

其中：M_k(x)= ${M_k}\left(\mathit{\boldsymbol{x}} \right) = \frac{1}{{\sqrt {2\sqrt {\mathtt{π} \sigma } } }}\exp \left({ - \frac{1}{{2{\sigma ^2}}}{{\left| {{y_k} - \sum\limits_{v \in {\xi _k}} {{h_{k, v}}{x_{k, v}}} } \right|}^2}} \right)$.

当达到最大迭代次数t_max后，用户j的发送码字被判决为

$ {\boldsymbol{{\hat x}}_\mathit{j}} = \arg \;\mathop {\max }\limits_{{\mathit{\boldsymbol{x}}_\mathit{j}}} \left( {\prod\limits_{k \in {\xi _j}} {M_{k \to j}^{{t_{\max }}}\left( {{\mathit{\boldsymbol{x}}_\mathit{j}}} \right)} } \right) $

(4)

1.2 SCMA码本与距离谱

对于用户的码字，其参与计算M_k(x)后用于更新MPA的消息M_k→j^t(x_j).为了使MPA正确地进行置信度传播，M_k(x)必须对加权和$\sum\limits_{j = 1}^J {{\text{diag}}} \left({{\mathit{\boldsymbol{h}}_j}} \right){\mathit{\boldsymbol{x}}_j}$有良好的区分度.具体来讲，如果对于J个用户任意不同2种传输码字X=[x₁, x₂, …, x_J]≠X′=[x′₁, x′₂, …, x′_J]，有加权和$\sum\limits_{j = 1}^J {{\text{diag}}} \left({{\mathit{\boldsymbol{h}}_j}} \right){\mathit{\boldsymbol{x}}_j} = \sum\limits_{j = 1}^J {{\text{diag}}} \left({{\mathit{\boldsymbol{h}}_j}} \right)\mathit{\boldsymbol{x}}_j^{'}$，则MPA无法区分传输码字X和X′.若MPA能正常工作，则码本需要满足唯一可译码性.在加性高斯白噪声信道下，所给码本唯一可译码性的严格定义如下.

定义1  对于J个用户任意不同2种传输码字X≠X′，若$\sum\limits_{j = 1}^J {{\mathit{\boldsymbol{x}}_j}} \ne \sum\limits_{j = 1}^J {\mathit{\boldsymbol{x}}_j^{'}} $，则码本满足唯一可译码性.

定义理想接收向量r_n=$\sum\limits_{j = 1}^J {{\mathit{\boldsymbol{x}}_j}} $.由于J个用户各有M个不同的码字，则r_n有M^J种取值.定义任意2种不同理想接收向量r_n和r_n′之间的欧氏距离为

$ d\left( {n,n'} \right) = \left\| {{\mathit{\boldsymbol{r}}_\mathit{n}} - {\mathit{\boldsymbol{r}}_{\mathit{n'}}}} \right\| $

(5)

其中：n≠n′且n, n′=1, 2, …, M^J，‖·‖为向量的欧氏范数.很明显，定义1所述唯一可译码性的等价条件为理想接收向量之间的最小欧氏距离min {d(n, n′)}不为0.如果min {d(n, n′)}不为0且越大，则MPA的检测效果越好.作为该设想的证明，将M^J种r_n等效为某个星座中的星座点，利用构造星座最大似然检测错误概率一致边界的方法^[13]，可得该星座的错误概率一致边界为

$ \begin{array}{l} \frac{{{N_{\min }}}}{{{M^J}}}Q\left( {\frac{{\min \;\left\{ {d\left( {n,\mathit{n'}} \right)} \right\}}}{{ {\sqrt {2{N_0}} } }}} \right) \le {P_\text{e}} \le \\ \left( {{M^J} - 1} \right)Q\left( {\frac{{\min \;\left\{ {d\left( {n,n'} \right)} \right\}}}{{\sqrt {2{N_0}} }}} \right) \end{array} $

(6)

其中：Q(·)为正态分布的互补累计分布函数，N_min为星座上与至少一个其他点相距min {d(n, n′)}的点数，N₀/2为噪声方差.如果码本不满足唯一可译码性，则min {d(n, n′)}=0，由式(6)可知，此时一致边界在高信噪比处是不随信噪比变化的直线，MPA将无法正常工作；在满足唯一可译码性的前提下，由于Q(·)为减函数，如果min {d(n, n′)}越大，则在高信噪比处错误概率P_e越小，因此设想成立.

综上，最优码本应该满足：理想接收向量之间的最小欧氏距离不为0，且尽可能大.定义距离谱Φ，其元素χ为由用户码本B₁, B₂, …, B_J求得的理想接收向量r_n之间的欧氏距离.上述最优码本设计准则可表示为

$ \mathit{\boldsymbol{B}}_1^*,\mathit{\boldsymbol{B}}_2^*,{\rm{\cdot\cdot\cdot,}}\mathit{\boldsymbol{B}}_J^* = \arg \;\mathop {\max }\limits_{{\mathit{\boldsymbol{B}}_{\rm{1}}},{\mathit{\boldsymbol{B}}_{\rm{2}}},{\rm{\cdot\cdot\cdot}},{\mathit{\boldsymbol{B}}_\mathit{J}}} {\chi _{\min }} $

(7)

其中χ_min为用户码本距离谱Φ的最小元素.

2 SCMA码本设计 2.1 码本设计方案

由图 1可知，给定J个用户星座，就能得到各用户的码本.为了降低设计复杂度，Taherzadeh等^[4]提出可以仅设计一个多维星座，对该星座加以针对每个用户的星座运算就能得到各用户星座，进而获得各用户的码本.

在这种方案中，码本性能依赖于多维星座和星座运算.多维星座的设计准则是：固定星座点之间的最小欧氏距离，最小化星座的平均功率^[14].这是一种难解的非凸二次约束二次规划问题.在接收端，若码本差异越大，则MPA的检测性能越好.当给定多维星座后，星座运算决定了用户码本之间的差异性，进而影响到MPA的检测性能，而确定最优的星座运算又存在一定难度.因此，设计多维星座的复杂度和确定最优星座运算的难度增加了码本设计的难度.

实际上，在Taherzadeh等^[4]所提码本设计方案中，各用户码本的非零行是多维星座各维度的坐标向量经过相位旋转和重新分配的结果^[15].在本文方案中，多维星座各维度的坐标向量仅有相位的不同，即各用户码本的非零行都由同一向量s₀∈$\mathbb{C}$^1×M经相位旋转得到.记s₀为基准向量，可表示为

$ \left[ {{\alpha ^{M/2 - 1}}r,{\rm{\cdot\cdot\cdot}},\alpha r,r, - r, - \alpha r,{\rm{\cdot\cdot\cdot,}} - {\alpha ^{M/2 - 1}}r} \right] $

(8)

其中：α∈[2, 4]为尺缩因子，r=0.5为基本尺度.定义码本矩阵G∈$\mathbb{C}$^K×JM，其第(j－1)M+1列到第jM列是用户j的码本B_j，即G=[B₁, B₂, …, B_J].给定因子图矩阵F，基准向量s₀与码本矩阵G的关系为

$ \left[ {{\mathit{\boldsymbol{G}}_{k,\left( {j - 1} \right)M + 1}},{\rm{\cdot\cdot\cdot}},{\mathit{\boldsymbol{G}}_{k,jM}}} \right] = \left\{ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{s}}_\mathit{i}},\;{\mathit{\boldsymbol{F}}_{\mathit{k,j}}} = 1}} \\ {{0,\;{\mathit{\boldsymbol{F}}_{\mathit{k,j}}} = 0}} \end{array}} \right. $

(9)

其中：s_i=e^jθ_is₀, i=0, 1, …, Kd_r－1，θ_i为旋转因子且θ₀=0，d_r为每个资源块上承载的用户数，0为M维全0行向量.式(9)表明，若F_{k, j}=1，则码本矩阵G的第k行、第(j－1)M+1列到第jM列与向量s_i, i=0, 1, …, Kd_r－1相同，而码本矩阵G的其余位置全为0.向量s₀, s₁, …, s_Kdr－1按照从左到右、从上到下的顺序依次放置在码本矩阵G中.

由基准向量s₀经相位旋转得到的码本矩阵G中，各用户码本的PAPR定义为

$ \begin{array}{l} 10\lg \left( {\mathop {\max }\limits_{1 \le m \le M} \left\{ {{{\left\| {\mathit{\boldsymbol{x}}_j^m} \right\|}^2}} \right\}/{E_{{\rm{avg}}}}} \right){\rm{dB}}\\ {\mathit{E}_{{\rm{avg}}}} = \frac{1}{M}\sum\limits_{m = 1}^M {{{\left\| {\mathit{\boldsymbol{x}}_j^m} \right\|}^2} = \frac{{2N{r^2}\left( {1 - {\alpha ^M}} \right)}}{{M\left( {1 - {\alpha ^2}} \right)}},\forall j} \end{array} $

(10)

其中：x_j^m为用户j的第m个码字.由式(10)可知，此时G中各用户码本的PAPR为10lg (Nr²α^M－2/E_avg)dB.随着码字个数M增加，这些用户码本将有较高的PAPR.为了避免高PAPR对实际系统产生不利影响，可以通过交织的方式降低PAPR^[5].交织过程可以表示为

$ \begin{array}{l} \mathit{\boldsymbol{v = }}\left[ {{\mathit{\boldsymbol{q}}_{\rm{1}}},{\mathit{\boldsymbol{q}}_{\rm{2}}},{\mathit{\boldsymbol{q}}_{\rm{3}}},{\mathit{\boldsymbol{q}}_{\rm{4}}}} \right]\\ \mathit{\boldsymbol{v' = }}\left[ {{\mathit{\boldsymbol{q}}_{\rm{3}}}, - {\mathit{\boldsymbol{q}}_4}, - {\mathit{\boldsymbol{q}}_1},{\mathit{\boldsymbol{q}}_{\rm{2}}},} \right] \end{array} $

(11)

其中：v′为v交织后的结果，q_i=[v_(i－1)M/4+1, …, v_iM/4]，v_l为v的第l个元素.本文方案仅交织码本中除去全0行后仍为偶数的行.经交织后，各用户码本的PAPR为10lg (r²(N_oα^M－2+N_e)/E_avg)dB，其中，N_o和N_e分别为用户码本中除去全0行后奇数行和偶数行的个数，且码本的非0行数N=N_o+N_e.对比交织前，码本的PAPR降低了10lg (Nα^M－2/(N_oα^M－2+N_e))dB.由于α∈[2, 4]，特别地，当(N, M)=(2, 4)时，码本的PAPR为0 dB，降低了2.041 2~2.747 0 dB；当M→∞时，码本的PAPR将降低约10lg(N/N_o)dB.给定图 2所示因子图矩阵F，一种由基准向量s₀通过相位旋转且经交织得到的码本矩阵G为

$ \mathit{\boldsymbol{G = }}\left[ {\begin{array}{*{20}{c}} {\bf{0}}&{{\mathit{\boldsymbol{s}}_\mathit{\boldsymbol{0}}}}&{{\mathit{\boldsymbol{s}}_{\rm{1}}}}&{\bf{0}}&{{\mathit{\boldsymbol{s}}_{\rm{2}}}}&{\bf{0}}\\ {{\mathit{\boldsymbol{s}}_{\rm{3}}}}&{\bf{0}}&{{{s'}_4}}&{\bf{0}}&{\bf{0}}&{{\mathit{\boldsymbol{s}}_{\rm{5}}}}\\ {\bf{0}}&{{{\mathit{\boldsymbol{s'}}}_{\rm{6}}}}&{\bf{0}}&{{\mathit{\boldsymbol{s}}_{\rm{7}}}}&{\bf{0}}&{{{\mathit{\boldsymbol{s'}}}_{\rm{8}}}}\\ {{{\mathit{\boldsymbol{s'}}}_{\rm{9}}}}&{\bf{0}}&{\bf{0}}&{{{\mathit{\boldsymbol{s'}}}_{{\rm{10}}}}}&{{{\mathit{\boldsymbol{s'}}}_{{\rm{11}}}}}&{\bf{0}} \end{array}} \right] $

(12)

其中：向量s′_i=[－re^jθ_i, αre^jθ_i, －αre^jθ_i, re^jθ_i]为交织向量s_i=[αre^jθ_i, re^jθ_i, －re^jθ_i, －αre^jθ_i]后的结果.

综上，若能确定尺缩因子和旋转因子，则可以获得各用户的码本B₁, B₂, …, B_J.因此，本文方案将多维星座的设计和星座运算的确定过程转化为了较简单的码本设计参数的选择过程，这一转化实际上降低了SCMA码本的设计难度.

2.2 低复杂度参数选择方法

由于θ₀=0且r=0.5，则B₁, B₂, …, B_J依赖于尺缩因子α和旋转因子θ₁, θ₂, …, θ_Kdr－1.结合式(7)所示码本设计准则可知，最优码本设计参数的选择方法为

$ \left\{ {\alpha^ *,\theta ^*_1, \cdots ,\theta _{K{d_r} - 1}^*} \right\} = \arg \mathop {\max }\limits_{\alpha ,\theta _{1}, \cdots ,{\theta_{{{Kd}_r} - 1}}} {\chi _{\min }} $

(13)

式(13)所示方法要求在给定取值范围和步长下，搜索这些参数所有可能的取值，然后以具有最大χ_min者作为最优码本设计参数.这种方法需要的搜索次数T为

$ T = N\left( \alpha \right) \times N\left( {{\theta _1}} \right) \times \cdots \times N\left( {{\theta _{K{d_r} - 1}}} \right) $

(14)

其中N(·)为给定取值范围和步长下括号中变量的取值个数.由于式(14)中T随资源块上承载的用户数d_r和资源块数K呈指数上升，当d_r和K过大时，式(13)所示参数选择方法因搜索复杂度过高而限制了实际应用.因此，需要寻找低复杂度参数选择方法.

记K维理想接收向量r_n的第k个元素为p_{k, n}.由于码字的稀疏性, p_{k, n}是占用第k个资源块的d_r个用户传输信号的叠加结果.此时，任意2个不同理想接收向量r_n和r_n′之间的欧氏距离可以表示为

$ d\left( {n,n'} \right) = \sqrt {\sum\limits_{k = 1}^K {\left| {{p_{k,n}} - {p_{k,n'}}} \right.\left| {^2} \right.} } $

(15)

由式(9)可知，在第k个资源块处，d_r个用户的传输信号分别取自d_r个向量s_(k－1)dr, …, s_kdr－1内的元素，而s_(k－1)dr, …, s_kdr－1由尺缩因子α和d_r个旋转因子θ_(k－1)dr, …, θ_kdr－1确定，因此，叠加结果p_{k, n}决定于α和θ_(k－1)dr, …, θ_kdr－1.具体来讲，对应K个资源块，将θ₀, θ₁, …, θ_Kdr－1每d_r项编为一组，共K组，则每组依次对应叠加结果p_{1, n}p_{2, n}, …, p_{K, n}.对于式(13)所示参数选择方法，如果存在k=1, 2, …, K，有α和θ_(k－1)dr, …, θ_kdr－1使得|p_{k, n}－p_{k, n′}|≠0，则θ₀, θ₁, …, θ_Kdr－1中除第k组外的其他组无论取何值，d(n, n′)一定不为0，即码本一定满足唯一可译码性.这表明在式(13)所示参数选择方法中，用θ₀, θ₁, …, θ_Kdr－1中满足|p_{k, n}－p_{k, n′}|≠0的分组替换其他分组后，不会影响码本的唯一可译码性.

因为对于任意k，总存在α和θ_(k－1)dr, …, θ_kdr－1使|p_{k, n}－p_{k, n′}|≠0，所以可用θ₀, θ₁, …, θ_Kdr－1中的任意一组替换其他分组.由于θ₀=0，第1组中待确定旋转因子的个数最少，所以本文方案用θ₀, θ₁, …, θ_dr－1替换θ₀, θ₁, …, θ_Kdr－1中的其他分组.此时，码本矩阵G中仅有d_r个不同的向量s₀, s₁, …, s_dr－1，可以按照拉丁顺序^[12]放置在码本矩阵G中.拉丁顺序要求码本矩阵G的行方向和列方向上不存在相同的向量s_i, i=0, 1, …, d_r－1.由于需要降低PAPR，如果s_i位于某个码本除去全0行后仍为偶数的行，则需要交织s_i.给定图 2所示因子图矩阵F，一种参数替换后满足拉丁顺序且经过交织的码本矩阵G为

$ \mathit{\boldsymbol{G = }}\left[ {\begin{array}{*{20}{c}} {\bf{0}}&{{\mathit{\boldsymbol{s}}_1}}&{{\mathit{\boldsymbol{s}}_0}}&{\bf{0}}&{{\mathit{\boldsymbol{s}}_{\rm{2}}}}&{\bf{0}}\\ {{\mathit{\boldsymbol{s}}_2}}&{\bf{0}}&{{{s'}_1}}&{\bf{0}}&{\bf{0}}&{{\mathit{\boldsymbol{s}}_{\rm{0}}}}\\ {\bf{0}}&{{{\mathit{\boldsymbol{s'}}}_2}}&{\bf{0}}&{{\mathit{\boldsymbol{s}}_0}}&{\bf{0}}&{{{\mathit{\boldsymbol{s'}}}_1}}\\ {{{\mathit{\boldsymbol{s'}}}_0}}&{\bf{0}}&{\bf{0}}&{{{\mathit{\boldsymbol{s'}}}_2}}&{{{\mathit{\boldsymbol{s'}}}_{\rm{1}}}}&{\bf{0}} \end{array}} \right] $

(16)

采用θ₀, θ₁, …, θ_dr－1替换θ₀, θ₁, …, θ_Kdr－1中其他分组的方法，式(13)所示参数选择方法可简化为

$ \left\{ {\alpha ^*,\theta _1^*, \cdots ,\theta _{{d_r} - 1}^*} \right\} = \arg \mathop {\max }\limits_{\alpha ,\theta _{1}, \cdots ,\theta_{{d_r} - 1}} {\chi _{\min }} $

(17)

此时，搜索次数T为

$ T = N\left( \alpha \right) \times N\left( {{\theta _1}} \right) \times \cdots \times N\left( {{\theta _{{d_r} - 1}}} \right) $

(18)

对比式(13)所示参数选择方法，式(17)中参数个数由Kd_r下降为d_r.这意味着在相同的参数取值范围和步长下，式(18)所示搜索次数将远小于式(14)所示搜索次数.同时，式(17)所示参数选择方法中参数个数与资源块数K无关，随着资源块数K上升，较之式(13)所示参数选择方法，式(17)所示参数选择方法在搜索复杂度上的优势将更加明显.

3 仿真结果及分析

本节仿真用于证明本文方案的误比特率性能.与本文方案对比的是文献[4]所提典型方案及文献[9]所提的现有且性能较好方案. SCMA系统参数(J, M, N, K)=(6, 4, 2, 4).因子图矩阵如图 2所示.信道模型为加性高斯白噪声信道.

仿真中，本文码本设计参数如表 1所示.基本尺度r=0.5. α∈[2, 4]且步长为0.1. θ₁, θ₂∈[0, 2π]且步长为0.02.为了便于比较，下文的χ_min已归一化，即

$ {\chi _{\min }} = \min \left\{ {d\left( {n,n'} \right)} \right\}/\sqrt {\frac{{\sum\limits_{n = 1}^{{M^J}} {{{\left\| {{{\boldsymbol{r}}_\mathit{n}}} \right\|}^2}} }}{{{M^J}}}} $

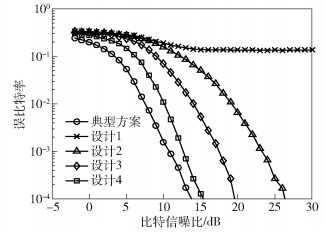
图 3显示了小于典型方案^[4]码本的χ_min时(典型方案中，χ_min=0.229)，在不同χ_min下，本文方案码本和典型方案码本的误比特率性能对比.如图 3所示，随着χ_min的减小，对应的设计4到设计1的误比特率性能较典型方案不断降低.特别地，对于χ_min=0的设计1，由于不满足唯一可译码性，其误比特率曲线在高信噪比处变为不随信噪比变化的直线，此时MPA无法正常工作.

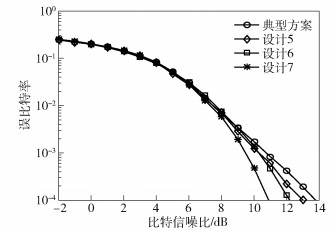
图 4显示了大于典型方案^[4]码本的χ_min时，在不同χ_min下，本文方案码本和典型方案码本的误比特率性能对比.如图 4所示，本文方案的误比特率性能随着χ_min的增大而不断提升.当误比特率为10^-4时，χ_min最大的设计7较典型方案信噪比可改善2.58 dB.

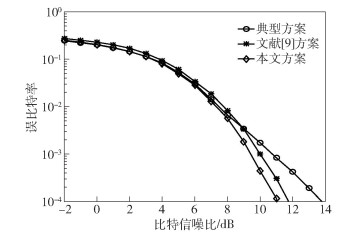
图 5为不同方案所得码本的误比特率性能对比.如图 5所示，本文方案码本的误比特率性能较文献[9]方案码本和典型方案^[4]码本都要好.经计算，典型方案码本、文献[9]方案码本及本文方案码本的χ_min分别为0.229 0、0.366 7和0.418 5.因此，本文方案性能的提升源于最大化了距离谱的最小元素χ_min.

4 结束语

提出了一种基于距离谱的SCMA码本设计方案.所提方案以参数选择的方式设计SCMA码本，从而避免了设计多维星座和确定最优星座运算带来的高码本设计复杂度.此外，通过不影响码本唯一可译码性的方式替换部分码本设计参数后，所提方案降低了参数选择的复杂度.通过分析码本对MPA具体过程的影响，以及采用交织降低码本PAPR的方法，所提方案以最大化交织后码本距离谱最小元素为目标，确定了最优的码本设计参数，最终获得了低PAPR且误比特率性能优异的SCMA码本.与现有码本设计方案相比，本文方案的性能得到显著提升.特别地，较之文献[4]提出的典型方案，本文方案性能提升了2.58 dB.