量子进化算法(QEA，quantum evolutionary algorithm)是以量子个体和量子基因位为基本进化单元，基于量子计算原理的一种概率优化方法^[1].由于其具有操作方便、优化目标清晰等优点，受到广泛关注^[2-3]，并已经在诸多领域得到应用^[4].虽然量子进化算法的进化过程简单明确，但同时其进化操作方式较为固定.如何深层次地挖掘该种类型进化算法的潜能，是一个需要研究的问题.分布式人工智能以及协同进化思想的出现，特别是以多智能体理论为代表的优化理论有力地促进了进化算法的繁荣.Zhong等^[5]提出一种多智能体的遗传算法，并将其应用于超高维函数优化等.潘晓英等^[6]将人类组织关系引入到智能体进化算法中，增强了算法的竞争和合作关系.Wang等^[7]提出一种采用量子编码的多智能体进化算法.吴亚丽等^[8]将知识模型与智能体模型相融合. Zheng等^[9]提出一种多智能体优化算法求解资源约束类型的项目调度问题.

当前所提出的多智能体进化算法、操作算子和进化方式单一，采用同一种群进化未免会使种群在后期进化动力不足.在考虑当前量子进化机制的特点和优越性后，受协同进化机制的启发^[10-11]，借鉴Fang等^[12]的思想，提出一种多层级之间协调进化的量子智能体进化算法，称为协同量子智能体进化算法(CQAEA，cooperative quantum agent evolutionary algorithm).

1 协同量子智能体进化算法 1.1 相关定义与概念

定义1 ^[8]   智能体：能够作用于自身和环境，并能对周围的环境做出反应的物理或抽象的实体.

定义2   量子智能体：以量子编码的智能个体，称之为量子智能体.

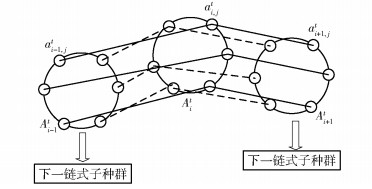
笔者提出的协同量子智能体进化算法，其3层进化空间结构如图 1所示，其中A_i^t表示第i个子种群，a_{i, j}^t表示第i个子种群的第j个个体.第t代种群的进化空间可以表示为X(t)={A₁^t, A₂^t, …, A_N^t}，其中N为子种群数目，每个子种群为A_i^t={a_{i, 1}^t, a_{i, 2}^t, …, a_{i, ψ}^t}，ψ为子种群的规模，则种群规模可以表示为Φ=ψ ·N，其中a_{i, j}^t(i=1, 2, …, N; j=1, 2, …, ψ)表示第t代第i个子种群中第j个量子个体，令l_{i, j, k}^t表示第t代第i个子种群中第j个量子个体的第k位，其中i=1, 2, …, N，j=1, 2, …, ψ，k=1, 2, …, L，L表示编码长度.

1.2 种群之间的操作 1.2.1 子种群之间置换个体

在第t次进化的过程中，A_i^t中的个体a_{i, i1}^t和子种群A_j^t中的个体a_{j, j1}^t进行交换，置换操作可以表示为：$A_{i}^{t}\leftarrow \left( \left( A_{i}^{t}\backslash a_{i, i1}^{t} \right)\cup a_{j, j1}^{t} \right), A_{j}^{t}\leftarrow \left( \left( A_{j}^{t}\backslash a_{j, j1}^{t} \right)\cup a_{i, i1}^{t} \right) $.

1.2.2 变换子种群连接关系

在第t次迭代过程中，A_i^t和A_j^t的互信息熵为

$ I\left( A_{i}^{t}, A_{j}^{t} \right)=-\sum\limits_{\left( \begin{smallmatrix} A_{i}^{t}\in X(t) \\ A_{j}^{t}\in X(t) \end{smallmatrix} \right)}{P}\left( A_{i}^{t}, A_{j}^{t} \right)\lg \frac{P\left( A_{i}^{t}, A_{j}^{t} \right)}{P\left( A_{i}^{t} \right)\left( PA_{j}^{t} \right)} $

(1)

定义$H=\left\{\begin{array}{ll}{a_{i, k}^{t}=0, } & {a_{j, k}^{t}=0} \\ {a_{i, k}^{t}=0, } & {a_{j, k}^{t}=1} \\ {a_{i, k}^{t}=1, } & {a_{j, k}^{t}=0} \\ {a_{i, k}^{t}=1, } & {a_{j, k}^{t}=1}\end{array}\right. $，则式(1)可变换为$I\left(A_{i}^{t}, A_{j}^{t}\right)=-\sum\limits_{H} P\left(A_{i}^{t}, A_{j}^{t}\right) \lg \frac{P\left(A_{i}^{t}, A_{j}^{t}\right)}{P\left(A_{i}^{t}\right)\left(P A_{j}^{t}\right)} $.

P(A_i^t, A_j^t)表示种群A_i^t和A_j^t中相互连接个体基因位处于不同状态时的联合概率密度，P(A_i^t)和P(A_j^t)表示相互连接个体处于对应状态时的概率密度.

若相似性满足I(A_i^t, A_j^t) < ξ时，断开2个子种群之间的连接关系，并进行种群的交换.

1.2.3 改变子种群之间个体连接关系

假定在子种群A_i^t和A_j^t中，量子智能体的连接关系为{(a_{i, i1}^t—a_{j, j1}^t)，(a_{i, i2}^t—a_{j, j2}^t)}，即第t代中的个体a_{i, i1}^t与a_{j, j1}^t相互连接，a_{i, i2}^t与a_{j, j2}^t相互连接.为有效提高进化种群的多样性，可将此时的连接关系更改为：{(a_{i, i1}^t—a_{j, j2}^t)，(a_{i, i2}^t—a_{j, j1}^t)}.

1.3 种群内部个体之间的操作 1.3.1 个体位置变换操作

对A_i^t中的量子智能体a_{i, i1}^t和a_{i, i2}^t，执行邻域个体互换操作以及任意个体互换操作.将量子智能体a_{i, i1}^t和a_{i, i2}^t相应量子位置进行互换，即执行swap(a_{i, i1}^t, a_{i, i2}^t)：Temp=a_{i, i1}^t，a_{i, i1}^t=a_{i, i2}^t，a_{i, i2}^t=Temp.

1.3.2 多亲个体交叉操作

以往文献采用的量子交叉与遗传交叉策略接近，潘晓英、吴亚丽等^{[6, 8]}采用了正交交叉，存在陷入局部极值的危险，全干扰交叉^[13]具备较强的局部搜索能力，但容易打破基因片段连接关系.刘振等^[14]采用边缘成绩模块交叉，因需要获取个体连接关系，会导致收敛速度较慢.本文提出基于基因位的3个体多亲交叉方法，3个相邻的量子智能体为{a_{i, k－1}^t, a_{i, k}^t, a_{i, k+1}^t}，步骤可描述如下：

步骤1   量子智能体a_{i, k}^t，选定交叉量子基因片段：D_k^t={l_{i, k, r}^t, l_{i, k, r+1}^t, …, l_{i, k, s}^t}.

步骤2   对所选择的3个量子智能体基因片段，执行swap(D_p^t, D_q^t)操作.

步骤3    k=k+1，判断交叉是否结束，否则转步骤1.

1.3.3 领域个体竞争操作

在子种群内进行领域个体竞争操作，第i个子种群的领域集合为

$ {{E}_{i}}=\left\{ \begin{array}{*{35}{l}} \left( a_{i, j}^{t}, a_{i, j+1}^{t} \right), & j=1, 2, \cdots , \psi -1 \\ \left( a_{i, 1}^{t}, a_{i, N}^{t} \right), & 其他 \\ \end{array} \right. $

(2)

个体相似性可表示为

$ d\left( {a_{i, j}^t, a_{i, j + 1}^\iota } \right) = \sqrt {\sum\limits_{j = 1}^k {\left( {l_{i, j, j}^t - l_{i, j + 1, j}^t} \right)} } $

(3)

若d(a_{i, j}^t, a_{i, j+1}^t) < d_min，则以概率p_com淘汰适应度较差的个体.

1.4 个体的自调整操作 1.4.1 个体的多粒度旋转操作

量子进化算法通常采用固定角度进行旋转，限制了个体多样性和种群寻优速度，采用多粒度旋转方法，多粒度旋转角设置为

$ {\theta _i} = \left\{ {\begin{array}{*{20}{l}} {c\left( {{f_i} - {f_{\min }}} \right)/\left( {\bar f - {f_{\min }}} \right), }&{{f_{\min }} \ne \bar f}\\ {c, }&{{f_{\min }} = \bar f} \end{array}} \right. $

(4)

其中：c∈[0.01π, 0.05π]为固定常数，f为种群的平均适应度，为最小适应度值.

1.4.2 个体的自适应变异操作

对量子智能体采用自适应动态变异，第t次迭代过程中的变异概率设置为

$ p_{m}(t)=p_{m} \mathrm{e}^{\left(1 / t / T_{\max }\right)} $

(5)

其中：T_max为循环迭代次数，p_m为变异概率初始值.

1.4.3 个体的局部扰动操作

利用最优个体可以探索优良解集空间，而较差个体则可扩大算法的寻优宽度和广度，从而可以有效地将勘探和开采操作结合起来.局部扰动操作如下.

步骤1   选择优良个体集合为

$ H_{b}^{t}=\left\{l_{i, j}^{t} | \text { fit }\left(l_{i, j}^{t}\right) \geqslant f_{m i}, j=1, 2, \cdots, \psi\right\} $

选择较差个体集合为

$ H_{w}^{t}=\left\{l_{i, j}^{t} | \text { fit }\left(l_{i, j}^{t}\right) \geqslant f_{m i}, j=1, 2, \cdots, \psi\right\} $

其中：fit(l_{i, j}^t)表示个体l_{i, j}^t的适应度，f_ma和f_mi分别为事先设定的阈值范围.

步骤2   分别针对H_b^t和H_w^t中的个体，扰动方法为l_{i, j, k}^t=l_{i, j, k}^t+rand(－0.1, 0.1)fit(l_{i, j}^t).同时判断更新前后的适应度值，若结果更优，则保留；否则撤销该操作.

步骤3   判断是否扰动完毕，否则转向步骤1.

通过上述步骤，提出协同量子智能体进化算法的具体步骤如下.

步骤1   确定量子染色体长度L、子种群数目和子种群内部个体数目等进化参数信息，同时确定进化过程的外在信息，如T_max、p_m、f_min和c等相关控制参数信息，循环迭代次数t=1；随机初始化量子智能体：X(0)={A₁(0), A₂(0), …, A_ψ(0)}.

步骤2  在子种群A_i^t(i=1, 2, …, ψ)之间进行个体置换操作，依据式(1)进行种群连接关系变更，并改变子种群之间个体连接关系.

步骤3   对子种群A_i^t，进行个体位置变换操作、多亲个体交叉操作、领域个体竞争操作.

步骤4   对于种群空间X(t)，按照式(4)进行量子智能体多粒度旋转操作，依据式(5)进行自适应动态变异操作，并对个体进行局部扰动操作.

步骤5   对X(t)中的所有个体进行一次测量，得到观测种群Q(t).

步骤6   判断是否满足收敛条件，满足则结束，输出最优解；否则t=t+1，转步骤2.

2 收敛性分析

引理1 ^[15](Bozlano-weierstrass定理)   所有有界的数列都有一个收敛的子序列.

定理1   笔者提出的协同量子智能体进化算法的进化空间X(t)是有限的，同时也是完备的.

证明

1) 给定的进化空间为X，则对于第t代进化空间中的个体x_m^t和x_n^t，在给定度量的情况下，U(x_m^t, x_n^t)=|f(x_m^t)－f(x_n^t)|满足度量空间的4条公理，(X, d)构成一个度量空间.

若采用λ进制进行编码，则个体的变化范围为(0, 0, …, 0)到(λ－1, λ－1, …, λ－1)，整个状态空间为Ω=λ^ΦL，因此种群进化空间X(t)是有限的.

2) 当进化代数满足t>t(ε)时，由于个体的迁移、交叉以及变异操作，较差个体逐步被替代，种群之间平均适应度$ \overline{fit}$不断提高，则存在某一数值ε，使得|f(x_m^t)－f(x_n^t)| < ε，故在种群的进化空间中柯西序列f(x(t))是存在的.

3) 根据柯西序列的定义，当ε=1时，则

$ \begin{aligned}\left|f\left(x_{m}^{t}\right)\right|=\left|f\left(x_{m}^{t}\right)-f\left(x_{n}^{t}\right)+f\left(x_{m}^{t}\right)\right| \leqslant \\\left|f\left(x_{m}^{t}\right)-f\left(x_{n}^{t}\right)\right|+\left|f\left(x_{m}^{t}\right)\right| <\\ 1+\left|f\left(x_{n}^{t}\right)\right| \end{aligned} $

令f_max=max{f(x_k^t), f(x_n^t)+1, k=1, 2, …, n}，则可得到对于任意的f(x_m^t)，满足f(x_m^t)≤f_max，故该柯西序列是有界的.

根据引理1，f(x(t))存在一个收敛的子序列f(x(r)(t))，使得$ \mathop {\lim }\limits_{t \to \infty } {\mkern 1mu} f\left( {{x}_{r}}(t) \right)=C$，C为固定常数，为子序列f(x(r)(t))的极限.对于柯西序列f(x(t))，当满足t>t(ε/2)时，则|f(x_m^t)－f(x_n^t)| < ε/2，对于其子序列f(x(r)(t))中的某一个数值f(x_{r, s}(t))，当t>t(ε/2)时，满足|x_{r, s}(t)－C| < ε/2，故得到

$ \left|f\left(x_{m}^{t}\right)-C\right|=\left|f\left(x_{m}^{t}\right)-x_{r, s}(t)+x_{r, s}(t)-C\right| \leqslant \\ {\left|f\left(x_{m}^{t}\right)-x_{r, s}(t)\right|+\left|x_{r, s}(t)-C\right| <} \\ {\varepsilon / 2+\varepsilon / 2=\varepsilon} $

即|fit(x_m^t)－C| < ε/2，从而证明了任意柯西序列收敛于同一极限，得到柯西序列是收敛的.

根据完备性的定义，可获得该进化空间X(t)是完备的，定理1得证.

定理2  笔者提出的协同量子智能体进化算法，其进化空间X(t)是紧的.

证明  对于种群空间X(t)中的任意序列x(t)，假定x(t)构成的空间为M_x，其内部的任意2个个体之间的距离上界表示为：δ(M_x)=sup|f(x_p^t)－f(x_q^t)|.由定理1可知，种群进化空间状态是有限的，故可知δ(M_x)只能在有限值范围内取值，故M_x是有界的，从而可得到x(t)是一个有界序列.又由引理1和定理1得到，x(t)含有一个收敛的子序列，可得到状态空间X(t)是紧的，定理2得证.

引理2 ^[15]   在有限维赋范空间中，任一子集$M \subset X $ 当且仅当为有界闭集时，才是紧集.

定理3   提出的协同量子智能体进化算法其进化空间X(t)是有界的，同时也是闭的.

证明   由于进化空间X(t)为紧的，故根据引理2，可以得到其空间状态为有界的，并且是闭合的.

引理3 ^[15](巴拿赫不动点定理)  假定X=(X, d)是一个非空的完备度量空间，T:X→X是在X上的压缩映射，则T恰好有一个不动点.

定理4  任意给定初始群体的情况下，笔者提出的协同量子智能体进化算法收敛于唯一不动点f^*.

证明  由定理2可知，进化空间X(t)在给定度量条件下为完备度量空间，同时该进化空间也是非空的，故只需证明在进化空间X(t)内部存在一个压缩映射即可.令f_M=max{f(x_k^t), k∈[1, N]}，0 < U < f_M，U为正实数，定义映射：T(x_k^t)=(U ·f(x_k^t)－U/2)/f_M，则此时

$ \begin{aligned} d\left(T\left(x_{m}^{t}\right), T\left(x_{n}^{t}\right)\right) &=U\left(f\left(x_{m}^{t}\right)-f\left(x_{m}^{t}\right)\right) / f_{M}=\\ \frac{U}{f_{M}}\left(f\left(x_{m}^{t}\right)-f\left(x_{m}^{t}\right)\right) \end{aligned} $

令$\varphi=\frac{U}{f_{M}}, 0 <\varphi <1 $，推理得到

$ \begin{aligned} d\left(T\left(x_{m}^{t}\right), T\left(x_{n}^{t}\right)\right) &=\varphi\left(f\left(x_{m}^{t}\right)-f\left(x_{m}^{t}\right)\right) \leqslant \\ \varphi | f\left(x_{m}^{t}\right) &-f\left(x_{m}^{t}\right) |=\\ \varphi d\left(x_{m}^{t}, x_{n}^{t}\right) \end{aligned} $

即d(T(x_m^t), T(x_n^t))=φd(x_m^t, x_n^t)，所以T为一个压缩映射，由引理3可以得到，映射T(x_k^t)能够收敛于唯一不动点，又因为T(x_k^t)=(Uf(x_k^t)－U/2)/f_M，从其构造可以看出，T(x_k^t)收敛于唯一不动点的充要条件为f(x_k^t)收敛到唯一不动点.即满足$T\left( x_{k}^{t} \right)=\mathop {\lim }\limits_{t \to \infty } \left( \left( Uf\left( x_{0}^{t} \right)-U/2 \right)/{{f}_{M}} \right)={{f}^{b}} $，也就是说，T(x_k^t)趋向于唯一的不动点f^b时，协同量子智能体进化算法的适应度函数f(x_k^t)满足$ \lim \limits_{t \rightarrow \infty} f\left(x_{k}^{t}\right)=\frac{f^{b} f_{M}+U / 2}{U}$，令$ {{f}^{*}}=\frac{{{f}^{b}}{{f}_{M}}+U/2}{U}$，故笔者所提出的协同量子智能体进化算法必定能收敛于唯一不动点f^*，同时与初始的种群f^*无关，显然f^*即为全局最优极值点，定理4得证.

3 仿真分析

将提出的协同量子智能体进化算法利用f₁~f₈函数进行仿真分析，仿真计算机配置为：处理器为Intel(R) Core(TM) i3-3220，内存2.00 GB，系统为Window7，仿真软件为Matlab R2009a.设定T_max=100，p_m=0.05，ψ=50，N=8.

$ f_{1}(x)=-\cos \left(x_{1}\right) \cos \left(x_{2}\right) \exp \left(-\left(x_{1}-\pi\right)^{2}-\left(x_{2}-\right.\right.\\ {\left.\boldsymbol{\pi})^{2}\right) \quad x_{i} \in[-100, 100]} \\ {f_{2}(x)=100\left(x_{1}^{2}-x_{2}\right)^{2}+\left(1-x_{1}\right)^{2}, x_{i} \in[-2.048}, \\ {2.048]} $

$ \begin{array}{*{20}{l}} {{f_3}(x) = - \sum\limits_i^n i x_i^2, n = 2, {x_i} \in [ - 10, 10]}\\ {{f_4}(x) = \sum\limits_{i = 1}^n {x_i^2} , n = 2, {x_i} \in [ - 5.12, 5.12]} \end{array} $

$ \begin{array}{l}{f_{5}(x)=\left(x_{1}+2 x_{2}-7\right)^{2}+\left(2 x_{1}+x_{2}\right)^{2}, x_{i} \in[-10, 10]} \\ {f_{6}(x)=x_{1}^{2}+x_{2}^{2}+25\left(\sin ^{2} x_{1}+\sin ^{2} x_{2}\right), x_{i} \in[-\pi, \pi]}\end{array} $

$ \begin{array}{*{20}{l}} {{f_7}(x) = 10n + \sum\limits_{i = 1}^n {\left[ {x_i^2 - 10\cos \left( {2\pi {x_i}} \right)} \right], } }\\ {n = 30, {x_i} \in [ - 5.12, 5.12]}\\ {{f_8}(x) = \sum\limits_{i = 1}^n {{{\left( {\sum\limits_{k = 1}^i {{x_k}} } \right)}^2}} , n = 20, {x_i} \in [ - 30, 30]} \end{array} $

3.1 单峰函数对比结果

将提出的协同量子智能体进化算法(CQAEA)与基本量子进化算法(QEA)^[1]、刘振等^[14]提出的协同进化扩展紧致量子进化算法(CECQEA)、Pedro等^[16]提出的多智能体遗传算法(MAGSA)进行充分的对比分析.

对本文算法，首先以4个单峰基准函数f₁~f₄为例进行仿真分析，4种算法分别独立运行10次，统计平均最优值、均值及标准差，其中f₁函数的最优值为-1，其余函数的最优值为0，结果如表 1所示.

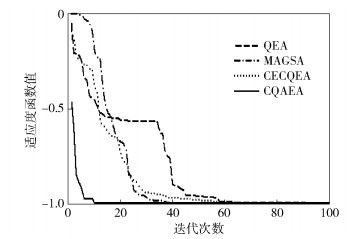
从表 1的统计结果可以看出，本文算法在最优值、均值以及标准差等方面都存在一定的优势，相比其他相关算法，本文算法能得到更优解，收敛结果也更为稳定，显示出算法良好的进化性能.与QEA和MAGSA相比，本文算法采用了分层的协同进化机制，增加了种群之间沟通和协调，因而充分考虑了种群的多样性信息，从而能够取得更好的效果，与CECQEA相比，进化的层级更为分明，不仅考虑种群之间的协同，也充分在种群内部和个体内部之间进行协同进化，增加了进化的深度和广度，从而取得的效果更优.为了更充分地进行对别分析，给出f₁的收敛迭代运行结果，如图 2所示.

从图 2可以看到，本文算法能够取得更优的收敛效果，算法具备较好的稳定性，利用较少的迭代次数就能稳定收敛，从而印证了表 1的统计结果.

3.2 多峰函数对比结果

对本文算法，以4个多峰基准函数f₅~f₈为例进行仿真对比分析.对比算法如3.1节，分别为QEA、MAGSA、CECQEA.

4种算法分别运行10次，统计其平均最优值(简称最优值)、均值及标准差，结果如表 2所示，其中4个多峰函数的理论最优值均为0.

从表 2可以看到，在优化多峰函数时，本文算法仍然存在一定的优势.由于多峰函数的特点，其在寻优过程中相比单峰函数更为复杂，也更容易陷入局部的极值，这在表 2中可以看出，整体的均值和标准差与表 1相比明显偏高，但同时也注意到本文算法具备良好的鲁棒性，能够保持良好的寻优性能，算法的均值和标准差都优于其他几种相关算法.

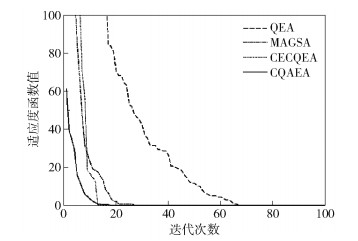
为了更充分地进行对比分析，给出f₅函数的仿真对比结果，如图 3所示.

从多峰函数的仿真对比结果可以看出，QEA存在寻优能力不足、效果不佳的情况，这在图 3能明显看到.同时也注意到，MAGSA和CECQEA优化效果较为接近，显示出2种进化算法各自的优势，本文算法则具备良好的收敛迭代效果.

4 结束语

依据量子编码和智能体进化理论的特性和进化优势，并基于协同进化的总体思想，提出协同进化机制的量子智能体进化算法.该算法实现了三级进化体制的有效结合，能够实现子种群之间的协同进化，保证子种群内部的充分交流.利用泛函分析中的不动点定理，对该进化算法的收敛性进行了证明，最后以一系列的仿真对该算法的优化性能进行了验证分析.从算法的仿真结果可以看出，所提出的CQAEA进化性能优越，但收敛速度还有待提高；另外收敛性证明过程还有些繁琐，这都是在以后的工作中需要进一步研究的方向.