车载应用服务要求低时延、高计算量，车辆自身有限的计算资源难以满足要求.为满足车载应用服务的要求，Zhang等^[1]提出车联网环境下的边缘计算(EC，edge computing)框架.在这个框架下服务提供商利用多层网络边缘服务器动态地服务于低延迟、高计算量的车载应用.车辆请求的车载服务数量过多导致网络边缘服务器超负荷.为减缓超负荷，网络边缘服务器需要卸载计算任务到边缘终端设备上，以提高效率.网络边缘服务器附近的停靠车辆(PV，parked vehicles)非常适合作为边缘终端设备.根据调查^[2]，约70%的私家车平均每天停靠20h以上.当车辆停靠时，它们的空闲资源可以长时间稳定地支持各种服务应用.例如，停靠车辆作为通信的中继节点，提供转发数据包^[3]和数据缓存服务^[4].

结合停靠车辆，提出一个基于停车协同的边缘计算卸载框架.在该框架下，服务提供商利用停车场中停靠车辆的空闲计算资源扩展网络边缘服务器的计算能力，卸载超负荷的计算任务给停靠车辆执行运算.利用真实停车场停靠车辆的数据，拟合停靠车辆在停车场的车流量模型，精准地预测出满足停留时长要求的停靠车辆数量.在预测的停靠车辆数量基础上，设计一个基于契约论的激励方案.在信息不对称的情况下，契约论不仅满足停靠车辆的效益，而且能够最大化服务提供商的效益.实验结果证明笔者提出的激励方案有效.

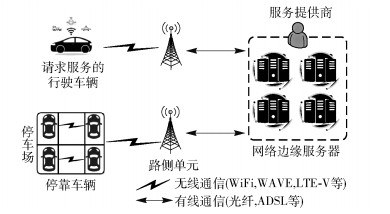
1 任务卸载系统框架 1.1 框架组成部分

如图 1所示，基于停车协同的边缘计算卸载框架由4部分组成.

1) 请求车辆.通过路侧单元节点，请求车辆向服务提供商请求各种车载应用服务，例如智能驾驶、虚拟现实等.

2) 服务提供商.通过租用网络边缘服务器，服务提供商直接处理请求车辆的计算任务.当网络边缘服务器超负荷时，服务提供商卸载计算任务给停靠车辆执行计算.

3) 停靠车辆.停靠车辆是被卸载计算任务的执行者.停靠车辆提供它们的空闲计算资源来扩展网络边缘服务器的计算能力，并执行卸载操作.

4) 路侧单元.路侧单元是网络边缘服务、停车场停靠车辆、请求服务车辆通信的桥梁.

1.2 系统工作流程

请求车辆在使用车载服务的过程中产生大量的计算任务.通过路边的路侧单元节点，车辆把计算任务上传给附近的网络边缘服务器.服务提供商通过网络边缘服务器执行计算任务.当计算任务数量过多，服务提供商需要把超负荷的计算任务卸载给附近停车场的停靠车辆.假设服务提供商需要卸载的计算任务为Q_c.根据文献[1], 计算任务和计算任务数据大小的关系为Q_c=γQ，其中：Q为计算任务的数据大小, γ为计算任务复杂度.服务提供商通过网络边缘服务器对停车场停靠车辆的车流量进行建模分析，预测出满足停留时长要求的停靠车辆数量，停靠车辆集合表示为M.服务提供商通过任务切分算法把超负荷的任务切分为M份并行计算的子任务^[1]，卸载M份子任务给M停靠车辆.停靠车辆通过空闲计算资源执行计算子任务，并返还结果给网络边缘服务器.最后，网络边缘服务器整合结果，并返还给请求车辆.

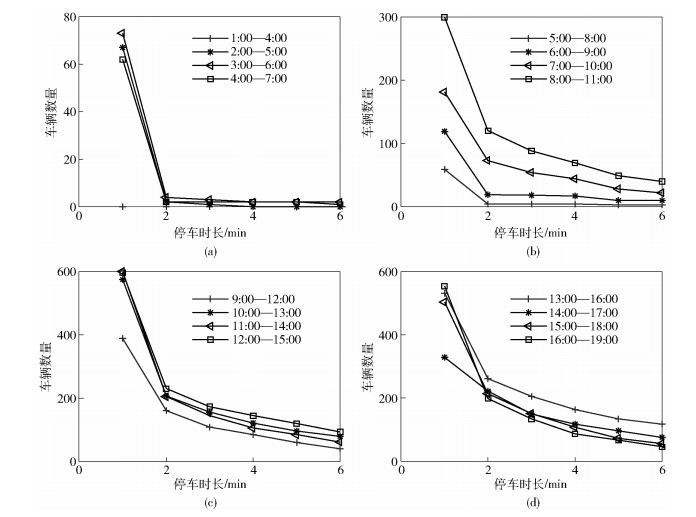
2 任务卸载模型 2.1 停车场车流量模型

利用停车场数据集，对停靠车辆不同时间点停留时长t_b的停靠车辆数量进行分析.停车场数据集是来自于澳大利亚堪培拉的公开数据集^[5].利用停车软件对马努卡购物区停车行为进行为期一个月采集，共采集180295条记录.主要采集每辆车的抵达和离开时间、停靠车位等信息.图 2所示为不同时间段的停留固定要求时间和停靠车辆数量的分布.在固定时间段内，停靠车辆停留时间越长，停靠车辆的数量越少.其他日期不同时段停靠车辆停留要求时间和停靠车辆数量的关系类似.通过上述历史数据，可预测不同时间段停靠车辆的数量M.

2.2 停靠车辆效益模型

服务提供商卸载x_m份计算任务给停靠车辆m，停靠车辆m获得p_m份奖励，p_m为给予停靠车辆m的激励，即

$ {R_m} = {p_m} $

(1)

停靠车辆停留时长t_b的概率s_m越大，服务提供商愿意卸载给停靠车辆更多的计算任务，相应的成本就越高^[6].对应的成本为

$ c_{{\rm{ml}}}^\iota = c{s_m}x_m^2 $

(2)

其中：c为计算任务单位成本, s_m为停留时长t_b的概率, x_m为数据的大小.停靠车辆有1－s_m的概率不会再继续停留t_b，可能会出现任务无法完成，需要对正在执行的任务进行迁移，保证任务继续被执行.根据文献[7]，迁移的成本为

$ c_{{\rm{m}}2}^\iota = \left( {1 - {s_m}} \right){c_r}x_m^2 $

(3)

其中：$c_{r}=\frac{\tau\left(\beta Q-\delta^{2} V_{\mathrm{thd}}\right)}{[\beta Q(1-\delta)]} $为中间变量；β是归一化参数；τ为迁移单位成本；δ=r_tra/r_mem为内存传输速率和内存占用率的比值，无量纲；V_thd为剩余占比内存的阈值，无量纲^[7].停靠车辆给与服务提供商手续费协助进行迁移.手续费与迁移成本是正比例关系，定义为

$ c_{m3}^\iota = \alpha c_{m2}^t $

(4)

其中：α为比例参数，无量纲.停靠车辆停留t_b的概率s_m越大，发生迁移的概率就越小，迁移成本c_m2^t越低，相应的激励成本越低.停靠车辆总成本为

$ {C_m} = c_{m1}^t + c_{m2}^t + c_{m3}^t $

(5)

停靠车辆的期望效益为

$ {U_m}\left( {{x_m},{p_m}} \right) = {p_m} - \frac{{x_m^2}}{{{\theta _m}}} $

(6)

其中：$ \frac{1}{\theta_{m}}=s_{m}\left(c-c_{r}\right)+c_{r}+\alpha c_{r}\left(1-s_{m}\right)$是成本类型，为刻画停靠车辆之间成本的差异性，把M辆停靠车辆的成本分为离散的I种类型.第i种类型的停靠车辆为L_i，L_i能够通过机器学习的方法预测得到.停靠车辆m的成本落到第i种类型中，即第i种类型，不失一般性，假设类型满足θ₁ < θ₂ < … < θ_I.第i种类型停靠车辆的效益为

$ {U_i}\left( {{x_i},{p_i}} \right) = {p_i} - \frac{{x_i^2}}{{{\theta _i}}} $

(7)

其中：p_i为第i种类型的车辆获得的激励，x_i为第i种类型的车辆卸载的任务数量，$ \frac{1}{{{\theta _i}}}$为第i种类型的车辆卸载的成本.

2.3 服务提供商效益模型

服务提供商卸载计算任务得到的利润为

$ {R_0} = \sum\limits_{i = 1}^I w {L_i}V\left( {{x_i}} \right) $

(8)

其中：V(x_i)为卸载x_i份计算任务得到的满意度，是一个凹函数；w为单位满意度赚到的利润.完成Q任务需要的激励成本为

$ {C_0} = \sum\limits_{i = 1}^I {{L_i}} {p_i} $

(9)

当停靠车辆无法完成卸载计算任务时，服务提供商协助进行迁移得到的手续费为

$ {S_0} = \sum\limits_{i = 1}^I {{L_i}} \alpha c_{i2}^t $

(10)

所以，服务提供商的效益函数为

$ \pi = \sum\limits_{i = 1}^I {{L_i}} \left[ {wV\left( {{x_i}} \right) - {p_i} + \alpha c_{i2}^t} \right] $

(11)

3 基于契约论的分配方法 3.1 问题描述

在信息不对称的条件下，服务提供商最大化自己的效益，同时满足停靠车辆的效益，是很大的一个挑战.因为在激励过程中，停靠车辆为获得更高的奖励会向服务提供商谎报自己的成本类型.为克服上述挑战，在信息不对称的前提下，契约论可以提供有力的工具去建模这种激励行为.服务提供商对于第i类型停靠车辆的策略定义为(x_i, p_i).策略(x_i, p_i)必须满足个体理性，即

$ {U_i}\left( {{x_i},{p_i}} \right) \ge 0,\forall i \in I $

(12)

个体理性约束条件能够保证停靠车辆的效益是非负的.对于最佳的策略(x_i, p_i)，第i类停靠车辆应该满足激励的相容性，即

$ {U_i}\left( {{x_i},{p_i}} \right) \ge {U_i}\left( {{x_j},{p_j}} \right),\forall i,j \in I,i \ne j $

(13)

激励相容性的约束条件能够确保不管停靠车辆选择高效益的合约或者是低效益的合约都会使其效益降低，只有选择对应自己类型的合约，它的效益才是最大的.所以，在激励相容性的约束条件下，停靠车辆没有动机隐藏它的成本类型，而是真实地选择了对应自己的类型.满足激励相容性和个体理性的约束条件下，最大化服务提供商的效益，即

$ \begin{array}{l} \mathop {\max }\limits_{{p_i},{x_i},i \in I} \pi = \sum\limits_{i = 1}^I {\left[ {{L_i}wV\left( {{x_i}} \right) - {L_i}{p_i} + \alpha {L_i}c_{i2}^t} \right]} \\ {\rm{s}}.\;{\rm{t}}.\;\;{\rm{Cl}}:{U_i}\left( {{x_i},{p_i}} \right) \ge 0,i \in \{ 1,2, \cdots ,I\} \\ \;\;\;\;\;\;{\rm{C}}2:{U_i}\left( {{\theta _i},{x_i},{p_i}} \right) \ge {U_i}\left( {{\theta _i},{x_j},{p_j}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;i,j \in \{ 1,2, \cdots ,I\} \\ \;\;\;\;\;\;{\rm{C}}3:\sum\limits_{i = 1}^I {{L_i}} {x_i} = Q\\ \;\;\;\;\;\;{\rm{C}}4:{x_i},{p_i} \ge 0,i \in \{ 1,2, \cdots ,I\} \end{array} $

(14)

其中：C1为个体理性约束条件, C2为激励相容性约束条件, C3为限制卸载多份子任务之和，等于总任务Q, C4保证卸载子任务和激励2个变量为非负.

3.2 求解方法

上述问题共有$\frac{I^{2}+3 I+2}{2} $个约束条件，当I很大时，解决它是很复杂的.为更加有效地解决上述问题，首先定义以下4个引理.

引理1   对于任意的合约(x, p)，有x_i < x_j，当且仅当p_i < p_j；有x_i=x_j，当且仅当p_i=p_j.

引理2  对于任意的合约(x, p)，有θ_i>θ_j，当且仅当x_i>x_j；θ_i=θ_j，当且仅当x_i=x_j.

引理3   对于个体理性的约束条件，第1种类型的个体理性满足，那么其他所有类型的个体理性就能满足, 即

$ {U_1}\left( {{x_1},{p_1}} \right) \ge 0 $

(15)

引理4   在给定局部向下激励约束的前提下，所有向下激励约束都会自动保持，并可以减少，即

$ {U_i}\left( {{x_i},{p_i}} \right) \ge {U_i}\left( {{x_{i - 1}},{p_{i - 1}}} \right),i \in \{ 2,3 \cdots ,I\} $

(16)

同理，所有的向上激励约束也都可以被移除，即

$ {U_i}\left( {{x_i},{p_i}} \right) \ge {U_i}\left( {{x_{i + 1}},{p_{i + 1}}} \right),i \in \{ 1,2, \cdots ,I - 1\} $

(17)

4个引理的证明参考文献[8-9].根据引理3，C1的I个约束减少为1个约束，即C5；根据引理1、2、4，C2的$\frac{I(I-1)}{2} $ 2个约束减少为I－1个约束，即C6.

优化问题(14)转变为

$ \begin{array}{l} \mathop {\max }\limits_{{p_i},{x_i},i \in I} \pi = \sum\limits_{i = 1}^I {\left[ {{L_i}wV\left( {{x_i}} \right) - {L_i}{p_i} + \alpha {L_i}c_{i2}^t} \right]} \\ {\rm{s}}.\;{\rm{t}}.\;\;\;{\rm{C}}5:{p_1} - \frac{{x_1^2}}{{{\theta _1}}} = 0\\ \;\;\;\;\;\;\;{\rm{C}}6:{p_i} - \frac{{x_i^2}}{{{\theta _i}}} = {p_{i - 1}} - \frac{{x_{i - 1}^2}}{{{\theta _i}}},i \in \{ 2, \cdots ,I\} \\ \;\;\;\;\;\;\;{\rm{C}}3:\sum\limits_{i = 1}^I {{L_i}} {x_i} = Q\\ \;\;\;\;\;\;\;{\rm{C}}4:{x_i},{p_i} \ge 0,i \in \{ 1,2, \cdots ,I\} \end{array} $

(18)

迭代C5和C6，得到$ {p_i} = \frac{{x_1^2}}{{{\theta _1}}} + \sum\limits_{k = 1}^i {{\mathit{\Delta} _k}} ,i \in I$，其中Δ₁=0和$\mathit{\Delta}_{k}=\frac{x_{k}^{2}}{\theta_{k}}-\frac{x_{k-1}^{2}}{\theta_{k}}, 1 <k \leqslant N $.把p_i代入优化问题(见式(18))，式(18)进一步转化为

$ \begin{array}{l} \mathop {\max }\limits_{{x_i},i \in I} \pi = \sum\limits_{i = 1}^I {\left[ {{L_i}wV\left( {{x_i}} \right) - {g_i}x_i^2 + \alpha {L_i}c_{i2}^t} \right]} \\ {\rm{s}}.\;{\rm{t}}.\;\;\;{\rm{C}}3:\sum\limits_{i = 1}^l {{L_i}} {x_i} = Q\\ \;\;\;\;\;\;\;{\rm{C}}7:{x_i} \ge 0,i \in \{ 1,2, \cdots ,I\} \end{array} $

(19)

其中：$ g_{i}=\frac{L_{i}}{\theta_{i}}+\left(\frac{1}{\theta_{i}}-\frac{1}{\theta_{i+1}}\right) \sum_{j=i+1}^{I} L_{j}, i <I$和${g_i} = \frac{{{L_I}}}{{{\theta _I}}} $, i=I.优化问题(见式(19))为凸优化问题，采用凸优化工具求解最优的x_i^*, $\forall $ i∈I.把x_i^*(i∈I)代入$ {p_i} = \frac{{x_1^2}}{{{\theta _1}}} + \sum\limits_{k = 1}^i {{\Delta _k}} , i \in I$，求出最优的p_i^*(i∈I).

4 仿真结果

Hou等^[8]提出线性契约论和信息不对称的斯坦伯格博弈方案，与笔者提出的方案进行了对比.假设服务提供商效益函数为V(x)=d+bx－ax²，参考文献[9-10]，参数设定如下.

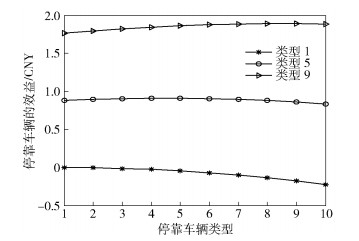
为验证个体理性和激励相容性2个约束条件，图 3显示了停靠车辆类型为1、5、9的效益.当停靠车辆选择它们对应的合约时，它们的效益才是最大的.对于类型5，只有选择第5个合约它的效益才是最大的，选择其他的合约都会导致它的效益降低.进一步观察到，每个类型的车辆效益都是非负的，且车辆效益的最大值随着类型的增加而增加.也就是说，它们都满足个体理性和激励相容性2个约束条件，从而克服信息不对称的难题.

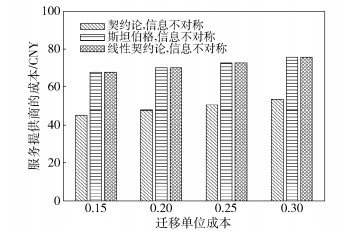
图 4所示为完成相同任务Q时，3种方案的成本与τ的关系. 3种方案随着τ的增加，成本相应地增加.因为随着τ增加，c_r增加，导致停靠车辆的成本增加，完成相同的任务Q，3种方案花费更多.在信息不对称的情况下，笔者提出的方案花费的成本小于斯坦伯格方案和线型契约论方案.因为提出的方案能够判断停靠车辆的类型，针对不同类型设计不同的价格和数量，进一步降低停靠车辆的效益或者减少成本.而斯坦伯格方案和线型契约论方案无法判断类型，不能针对不同类型做出对应的策略.

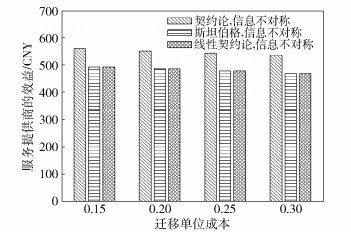
图 5所示为完成相同的Q任务时，3种方案获得的效益与τ的关系.在信息不对称的情况下，所提方案获得的效益是大于斯坦伯格方案和线型契约论方案.

5 结束语

利用真实数据集精准地预测出停留固定要求时间的停靠车辆数量.在预测车辆数量的基础上，设计一个基于契约论的激励方案，以激励停靠车辆进行计算卸载.实验结果证明了新方案的有效性.下一步的研究工作将考虑停靠车辆的停车行为信息，以完善激励方案.