基于聚类算法的混合分类器构建的信息评分系统中,不合理的聚类值或者初始类簇中心点会严重影响分类精度的问题,对此,提出了2种基于模糊粗糙集实例选择的新型混合算法.这2种算法仅与数据集的数据结构有关,不受其他外部参数影响.实验结果表明,基于模糊粗糙集实例选择的2种混合算法针对不同结构的数据集表现出了各自的特性,深化了对数据集的理解,提高了准确率.
For the credit scoring system built on cluster algorithm based hybrid classifier, the unreasonable clusters number or starting center points of each cluster have severely negative influence on the classification accuracy. In order to solve the problem, two new hybrid algorithms based on fuzzy-rough instance selection were proposed respectively, which are only related to intrinsic data structure of datasets and are not affected by other external parameters. The experimental results show that the proposed hybrid algorithms exhibit their own characteristics for datasets with different structures, which deepens the understanding of data sets and improves the accuracy.
信用评分技术用于甄别好坏申请者和评估潜在风险,在金融风险控制领域扮演着重要的角色[1].在构建信用评分系统过程中,大数据技术挖掘历史信贷数据中的高价值特征来鉴别高风险申请者[2].
由于冗余和无关特征的影响,基于单个分类器的信用评分系统往往精度不高,研究表明特征选择能够有效提升单分类器性能[3-5].此外,孤立和不一致的实例也会严重影响分类器的性能,因此研究人员设计出基于聚类算法的混合分类器[6],用自组织映射(SOM,self-organizing maps)算法确定聚类值和初始类簇中心点.然后用k-means算法进行聚类,将实例分配到相应的类并剔除每类的非典型实例.由于没有既定的规则用于选择最佳参数,因此SOM和k-means算法的参数都需要通过反复试验确定.另外,不合理的聚类值或者初始类簇中心点会严重影响聚类结果.实例选择技术也可以有效地甄别非典型数据,国内许多研究人员对该技术进行了深入的研究[7-10].基于模糊粗糙集理论(FRST,fuzzy-rough set theory)[11]的实例选择(FRIS,fuzzy-rough instance selection)技术[12],仅利用FRST的正域剔除噪声实例,有效提升数据质量和训练时间,并在一些领域取得了成功的应用[13-14],但还尚未应用在信用评分领域.
提出了一种应用在信用评分领域的基于FRIS的新型混合算法,并探讨了基于文献[12]中两种FRIS方法的混合分类器.实验结果表明,新型混合算法获得了较好的准确率,并且在不同结构的数据集上展现了各自的优势,深化了对数据集的认识.
1 背景知识 1.1 粗糙集分析在粗糙集理论中[15], 数据被视为信息系统(U, S), 其中U和S分别为实例和特征的有限非空集合. S中每一项a都对应U→Va的映射, 其中Va为a在实例集合U上的值域.对于特征集合S的每一个子集B,衡量实例间可区分程度的指标——不可区分关系RB定义如下:
| $ {{R}_{B}}=\left\{ (x, y)\in {{U}^{2}}\text{且}(\forall a\in B)(a(x)=a(y)) \right\} $ | (1) |
显而易见, RB是等价关系.对于B的不可区分关系的等价类记为[x]RB.对
| $ {{R}_{B}}\downarrow A=\left\{ x\in U|{{[x]}_{{{R}_{B}}}}\subseteq A \right\} $ | (2) |
| $ {{R}_{B}}\uparrow A=\left\{ x\in U|{{[x]}_{{{R}_{B}}}}\cap A\ne \varnothing \right\} $ | (3) |
通过包含决策特征可以把信息系统扩展为决策系统(U, S∪{d})[16],其中
| $ \text{PO}{{\text{S}}_{B}}={{\cup }_{x\in X}}{{R}_{B}}\downarrow {{[x]}_{{{R}_{d}}}} $ | (4) |
若x∈POSB, 对于任何实例,只要其在B中的特征与x取值相等,那么该实例就与x具有相同的决策类.
1.2 模糊粗糙集将粗糙集上下近似公式(式(2)和式(3))扩展到模糊情况,可以把模糊集和粗糙集整合到一起[11].
对于S的任意子集B, 定义模糊集B的不可区分关系如下:
| $ (x, y)=\mathscr{T} \underbrace{\left(R_{a}(x, y)\right)}_{a \in B} $ | (5) |
其中:
对U中的y,根据上述不可区分关系,定义模糊集B的正域为
| $ \operatorname{POS}_{B}(y)=\left(\cup_{x \in X} R_{B} \downarrow R_{d} x\right)(y) $ | (6) |
由于式(6)的计算代价过高,当决策特征是离散值时,用式(7)代替[17]:
| $ \operatorname{POS}_{B}^{\prime}(y)=\left(R_{B} \downarrow R_{d} y\right)(y) $ | (7) |
首先介绍几种典型FRIS技术的实现原理及优缺点,并在此基础上提出基于FRIS的混合算法.
2.1 典型FRIS技术FRIS的核心思想是利用正域信息判断实例的有用程度以及是否应该保留.
对决策系统(U, S∪{d}), 令a为(U, S∪{d})中的数值型特征,取值范围是l(a).为了表示x和y两个实例对特征a的近似相等,采用下述模糊关系Ra[12]:
| $ R_{a}^{\alpha}(x, y)=\max \left(0, 1-\alpha \frac{|a(x)-a(y)|}{l(a)}\right) $ | (8) |
其中参数α(α≥0)决定Raα的颗粒度.式(8)并非是定义实例x和y之间基于特征a的相似度的唯一假设,可根据需要采取其他形式的模糊关系公式.
文献[12]中介绍了3种FRIS方法,但FRIS-III方法的计算过于复杂,因此选择FRIS-I和FRIS-II探索其在信用评分系统混合算法中的优势. FRIS-I方法如下文所述,其计算每个实例对正域的隶属度,剔除隶属度小于门限参数τ的实例. FRIS-I方法简单高效,但由于其是根据固定门限参数剔除实例,没有考虑实例剔除后正域的变化,因此通常会剔除比实际更多的实例.
FRIS-I(S, α, τ)
输入:
S, 将被约简的实例集合;
输出:
Y,约简后的实例集合;
参数:
α, 颗粒度参数;
τ, 自定义门限.
1 Y←S
2 foreach x∈S
3 if(POSAα, S(x) < τ)
4 Y←Y-{x}
5 return Y
针对FRIS-I方法的弊端,FRIS-II方法每次剔除隶属度最小的实例,然后重新计算每个实例对新数据集正域的隶属度,反复迭代直到所有实例都完全属于正域.与FRIS-I方法相比,其不需要预先设定门限参数,通过动态的正域来剔除噪声实例.
FRIS-II(S, α)
输入:
S, 将被约简的实例集合;
输出:
S, 约简后的实例集合;
参数:
α, 颗粒度参数.
1 while(true)
2 z←0, ρz←1
3 foreach x∈S
4 if(POSAα, S(x) < ρz)
5 z←x
6 ρz←POSAα, S(x)
7 if (z≠0)
8 S←S-{z}
9 else return S
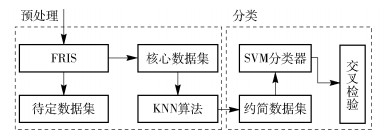
2.2 混合算法笔者提出的信用评分模型的统一算法框架如图 1所示,将FRIS-I和FRIS-II分别应用在该框架里构建混合分类器,详细流程如下.
|
图 1 混合算法架构 |
步骤1 初始化FRIS参数:(α, τ)或者α.计算数据集中每个实例的隶属度并根据相应的规则剔除实例,被剔除的实例归到待定数据集.
步骤2 保留的实例纳入核心数据集.用KNN算法检查待定数据集,凡是KNN算法预测类别与实际类别相同的实例一律重新纳入约简后的数据集,形成约简数据集.
步骤3 在约简数据集上应用SVM分类器,并引入交叉检验提升模型的泛化能力.
步骤4 验证不同的参数组合,得到产生最小交叉检验分类误差的最佳参数组合.
步骤5 对2个分类器使用最佳参数组合构建高性能的混合分类器.
3 实验结果UCI机器学习库[18]中的German和Australian信用数据集是2个广泛用于信用评分算法评估的数据集,使用这2个数据集验证算法便于与其他的研究成果比较.数据集的基本情况如表 1所示.
|
|
表 1 数据集概况 |
在Ubuntu系统用R语言仿真实验结果,首先在KNN算法中令参数k=5,并分别采用线性、多项式和RBF 3种不同核函数的SVM算法(分别简记为SVML、SVMP和SVMR)对约简后的数据集建模.为了便于重复实验结果,随机种子设为123.为了得到可靠稳定的模型,在数据集上应用10折交叉检验(10-CV)[19]和弃一法交叉检验(LOO-CV)[20],并比较分类精度和约简后的实例数. 2种交叉检验法都是利用规则将原始数据进行分组,一部分作为训练集;另一部分作为测试集,循环遍历计算每次分组结果并平均得到最终模型. 10-CV与LOO-CV不同之处在于分组规则和计算量不同,前者将数据均分为10折,计算10次;后者每次取一个数据作为分组,计算次数等于数据集大小.
为了得到更好的分类精度,在仿真中为每个核函数构建参数搜索网格,以期获得最佳的参数组合.
3.1 混合分类器1的实验结果表 2~表 7显示了混合分类器1(HC1,hybrid classifier 1)在不同颗粒度系数和门限系数参数组合时经2种交叉检验后的分类精度和约简后实例数.当颗粒度系数取值较大时,实例选择能力不显著,故此处选择实例选择作用明显的区间[0.2,1.0].门限系数取值过小,则剔除噪声能力变差,此处选择{0.7,0.8,0.9}3个值来观察噪声数据剔除情况.
|
|
表 2 τ=0.7时HC1的实例数和分类精度(German信用数据) |
|
|
表 3 τ=0.8时HC1的实例数和分类精度(German信用数据) |
|
|
表 4 τ=0.9时HC1的实例数和分类精度(German信用数据) |
|
|
表 5 τ=0.7时HC1的实例数和分类精度(Australian信用数据) |
|
|
表 6 τ=0.8时HC1的实例数和分类精度(Australian信用数据) |
|
|
表 7 τ=0.9时HC1的实例数和分类精度(Australian信用数据) |
从分类结果来看,2个信用数据集在2种交叉检验下的最佳性能都是通过多项式核函数的SVM算法达到的. German信用数据集在2种交叉检验下的最佳分类精度分别是0.9832和0.9860,最优的实例数是713,是原始数据集大小的71.3%. Australian信用数据集在2种交叉检验下的最佳分类精度都是0.9187,最优的实例数是652,是原始数据集大小的94.5%.上述分析表明,German数据集中孤立实例和不一致实例的占比更大.
3.2 混合分类器2的实验结果表 8和表 9显示了混合分类器2(HC2)在不同颗粒度系数下经过2种交叉检验后的分类精度和约简后实例数.颗粒度系数的取值原则参考HC1.从整体上来看,依然是多项式核函数SVM算法性能最佳,但Australian数据集的最佳分类精度却是线性核函数SVM算法获得. German信用数据集在2种交叉检验下的最佳分类精度分别是0.9775和0.9788,并且取得最优值时的颗粒度参数相同,对应的最优实例数是709,是原始数据集大小的70.9%. Australian信用数据集在弃一法交叉检验下的最佳分类精度是0.9881,相应的实例数是505,为原始数据集大小的73.2%.与HC1相比,HC2不需要调整门限参数τ, 虽然German信用数据集的最佳分类精度略有下降,但约简数据集实例数更少.对于German信用数据集来说, HC2约简后的实例数介于HC1当τ分别取0.8和0.9得到的实例数之间. Australian信用数据集约简实例数在HC2中变化比较大,并且用更少的实例得到了比HC1中更好的分类精度, 这说明HC2获得了比HC1质量更好的约简数据集.
|
|
表 8 HC2的实例数和分类精度(German信用数据集) |
|
|
表 9 HC2的实例数和分类精度(Australian信用数据集) |
2种混合分类器与线性判别分析(LDA,linear discriminant analysis)、逻辑回归(LR,logistics regression)和神经网络(NN,neural network)等未做实例选择基准分类器[21]的最佳分类精度比较见表 10.从比较结果来看,2种混合分类器取得了明显优于基准分类器的分类精度,尤其是HC2对Australian数据集展示了更加强大的信用评估能力.对German数据集,2种混合分类器没有明显的分类精度差异.
|
|
表 10 不同算法对Australian和German信用数据集的分类精度 |
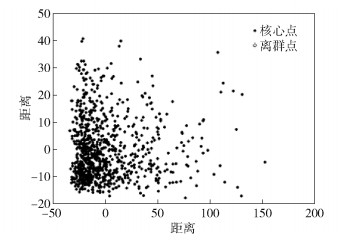
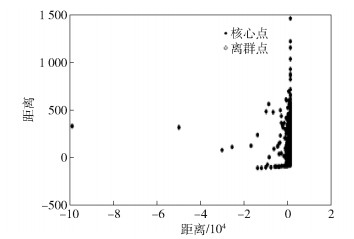
图 2和图 3是根据密度聚类算法[22]绘制的German和Australian数据集的MDS图. MDS图表明,German的数据分布比较分散,而Australian数据相对比较集中.从表 2~表 7可以看出, 固定τ值, German信用数据的约简结果随着α的改变而剧烈变化, 而Australian信用数据的约简结果却对比变化不大.再观察表 8和表 9, 随着α值的变化,2个数据集的约简结果变化趋势相似,约简结果完全由颗粒度系数决定.上述现象说明,由于German数据集分散的特性,HC1通过固定门限剔除了更多的孤立和不一致实例.而HC2通过动态的正域探索数据结构,比HC1剔除了更多的Australian数据集中的噪声实例,但却用更少的实例获得了更好的分类精度.从实验结果来看,HC1更适合分散型的数据集,而HC2对相对集中的数据集更加有效.
|
图 2 German数据集的MDS图 |
|
图 3 Australian数据集的MDS图 |
提出的基于FRIS的信用评分混合算法不受外部参数影响,通过选取适当的参数,性能要远远优于LDA、LR和NN等基准分类器.由于2种分类器的原理不同,HC1更适合分散型的数据集,而HC2对相对集中的数据集更加有效.在保证分类性能的情况下,同时约简实例和特征[23]是值得进一步探索的领域.
| [1] |
Yi Baiheng, Zhu Jianjun. Credit scoring with an improved fuzzy support vector machine based on grey incidence analysis[C]//IEEE International Conference on Grey Systems and Intelligent Services. New York: IEEE Press, 2015: 173-178.
|
| [2] |
Lahsasna A, Ainon R N, Wan T Y. Credit scoring models using soft xomputing methods:a survey[J]. The International Arab Journal of Information Technology, 2010, 7(2): 115-123. |
| [3] |
Ramya R S, Kumaresan S. Analysis of feature selection techniques in credit risk assessment[C]//International Conference on Advanced Computing and Communication Systems. New York: IEEE Press, 2015: 1-6.
|
| [4] |
Lin C C, Chang C C, Li F C, et al. Features selection approaches combined with effective classifiers in credit scoring[C]//IEEE International Conference on Industrial Engineering and Engineering Management. New York: IEEE Press, 2011: 752-757.
|
| [5] |
Yao Ping. Fuzzy rough set and information entropy based feature selection for credit scoring[C]//International Conference on Fuzzy Systems and Knowledge Discovery. New York: IEEE Press, 2009: 247-251.
|
| [6] |
Hsieh N C. Hybrid mining approach in the design of credit scoring models[J]. Expert Systems with Applications, 2005, 28(4): 655-665. DOI:10.1016/j.eswa.2004.12.022 |
| [7] |
田春娜, 高新波, 李洁. 基于嵌入式Bootstrap的主动学习示例选择方法[J]. 计算机研究与发展, 2006, 43(10): 1706-1712. Tian Chunna, Gao Xinbo, Li Jie. An example selection method for active learning based on embedded bootstrap algorithm[J]. Journal of Computer Research and Development, 2006, 43(10): 1706-1712. |
| [8] |
刘振兴.主动示例选择算法及其在人脸检测中的应用[D].西安: 西安电子科技大学, 2010.
|
| [9] |
韩光辉.基于欧式距离的实例选择算法研究[D].保定: 河北大学, 2011. http://www.cnki.com.cn/Article/CJFDTotal-SHDR201003005.htm
|
| [10] |
张宁.基于近邻分类的实例选择算法研究[D].保定: 河北大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10075-2010023974.htm
|
| [11] |
Dubois D, Prade H. Putting rough sets and fuzzy sets together[M]//SLOWINSKI R. Intelligent decision support. Berlin: Springer, 1992: 203-232.
|
| [12] |
Jensen R, Cornelis C. Fuzzy-rough instance selection[C]//International Conference on Fuzzy Systems. New York: IEEE Press, 2010: 1-7.
|
| [13] |
Jhawar A, Chan C S, Monekosso D, et al. Fuzzy-rough based decision system for gait adopting instance selection[C]//IEEE International Conference on Fuzzy Systems. New York: IEEE Press, 2016: 1127-1133.
|
| [14] |
Kang Xiaomeng, Liu Xiaopeng, Zhai Jjunhai, et al. Instances selection for NN with fuzzy rough technique[C]//International Conference on Machine Learning and Cybernetics. New York: IEEE Press, 2011: 1097-1100.
|
| [15] |
Pawlak Z. Rough sets: theoretical aspects of reasoning about data[M]. Norwell: Kluwer Academic Publishing, 1992.
|
| [16] |
Jensen R, Shen Qiang. Computational intelligence and feature selection: rough and fuzzy approaches[M]. Hoboken: Wiley, 2008.
|
| [17] |
Cornelis C, Jensen R, Hurtado G, et al. Attribute selection with fuzzy decision reducts[J]. Information Sciences, 2010, 180(2): 209-224. DOI:10.1016/j.ins.2009.09.008 |
| [18] |
Frank A, Asuncion A. UCI machine learning repository[EB/OL]. (2010-09-16). http://archive.ics.uci.edu/ml.
|
| [19] |
Geisser S. The predictive sample reuse method with applications[J]. Journal of the American Statistical Association, 1975, 70(350): 320-328. DOI:10.1080/01621459.1975.10479865 |
| [20] |
Geisser S. A predictive approach to the random effect model[J]. Biometrika, 1974, 61(1): 101-107. |
| [21] |
Yao Ping. Hybrid classifier using neighborhood rough set and SVM for credit scoring[C]//International Conference on Business Intelligence and Financial Engineering. New York: IEEE Press, 2009: 138-142.
|
| [22] |
Rodriguez, Laio A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492-1496. DOI:10.1126/science.1242072 |
| [23] |
Parthalain N M, Jensen R. Simultaneous feature and instance selection using fuzzy-rough bireducts[C]//IEEE International Conference on Fuzzy Systems. New York: IEEE Press, 2013: 1-8.
|



