2. 澳门大学 智能城市物联网国家重点实验室, 澳门 999078
为了满足高精度和高可靠性定位的需求,提出了一种基于扩展卡尔曼滤波的移动群体定位算法,把待定位的用户节点当成一个群组,利用他们之间的距离信息得到更好的定位性能,以减小环境噪声和无线信号不稳定造成的影响.此外,开发出一个实际的系统,并在大学校园里进行了大量实验.实验结果和理论分析验证了所提出方法的有效性.
2. The State Key Laboratory of Internet of Things for Smart City, University of Macau, Macao 999078, China
In order to meet the requirement of high localization accuracy and the high reliable localization in some scenarios, the user nodes to be located were taken as a group to get better localization performance by utilizing the mutual distance information among them. A mobile group localization method was designed based on extended Kalman filter, which can alleviate the influence caused by environmental noisy and unstable wireless signals. Besides, a real system was implemented and experiments were performed on the campus of University. The experimental evaluations prove that the performance of the proposed method can effectively improve the localization accuracy.
近几年,无线定位技术被广泛用于军事、工业、农业等诸多领域[1].提高定位系统的定位精度是亟待解决的核心问题[2-3].例如,在建造业,如果能够使用一定的方法实时监控工人的位置,对于即将出现的危险及时预警,就可以避免发生意外.
Wu等[4]提出了一种基于GPS和移动电话捕获的高精度定位方法,所设计的方法可将定位精度提高30%,但是定位场景较为局限,主要针对室外定位.在较为复杂的物联网三维定位场景中,传统三角定位算法Tri(triangulation)可能不适用[5].笔者提出了一种适用于三维自组织环境的基于空间离散化的PLI(position location information)获取算法.该方法可以使锚节点位置分布得更加合理,但是没有利用待定位节点的信息.传统三维定位算法高度依赖于信标节点[6],研究者大都没有考虑如果信标节点是恶意的[7],或者信标节点出现故障时的情况,仅提出了一种基于三维反馈校正的三角剖分算法FC-TDT(feedback correction based on three dimensional triangulation),避免信标节点的恶意定位.该方法可以避免恶意节点对定位性能的影响,但是并没有解决提高系统定位精度这一核心问题. Deng等[8]提出了一种基于扩展卡尔曼滤波EKF(extended Kalman filter)的非线性车辆运动定位预测算法.该方法的缺点是适用范围较小,对定位系统的要求高.还有些研究者提出使用移动锚点的方法来提高定位精度[9-10],但是由于该方法中移动锚点需要不断地进行自我定位,从而使其必需配备GPS等能进行自我定位的设备以及移动控制模块,大大增加了设备需求[11-13]和开发成本.
笔者提出了一种基于扩展卡尔曼滤波的移动群体定位算法,结合了协作定位和扩展卡尔曼滤波思想,把待定位节点当成一个群组,实现低复杂度、高精度的定位算法.
1 系统模型 1.1 状态方程假设用户保持匀速运动.在三维场景中,可以用坐标和速度描述一个用户的状态,此时用户i在t时刻的状态可以用向量表示为
| $ \boldsymbol{X}(t)=\left[L_{x}(t), L_{y}(t), L_{z}(t), V_{x}(t), V_{y}(t), V_{z}(t)\right] $ | (1) |
其中:Lx(t)、Ly(t)、Lz(t)为用户i此刻在坐标轴上x、y和z的值;Vx(t)、Vy(t)、Vz(t)是用户此刻在3个坐标轴上的速度分量.
用户的状态转移方程可以表示成
| $ \mathit{\boldsymbol{X}}(t/t - 1) = \mathit{\boldsymbol{F X}}(t - 1) + \mathit{\boldsymbol{W}}(t - 1) $ | (2) |
其中:W(t-1)表示状态方程存在的不确定性,在这里主要指高斯白噪声;F为状态转移矩阵,表示其状态由t-1时刻转化为t时刻.定义为
| $ \boldsymbol{f}=\left[\begin{array}{cccccc}{1} & {0} & {0} & {T} & {0} & {0} \\ {0} & {1} & {0} & {0} & {T} & {0} \\ {0} & {0} & {1} & {0} & {0} & {T} \\ {0} & {0} & {0} & {1} & {0} & {0} \\ {0} & {0} & {0} & {0} & {1} & {0} \\ {0} & {0} & {0} & {0} & {0} & {1}\end{array}\right] $ | (3) |
| $ \boldsymbol{F}=\left[\begin{array}{cccc}{\boldsymbol{f}} & {\boldsymbol{o}} & {\cdots} & {\boldsymbol{o}} \\ {\boldsymbol{O}} & {\boldsymbol{f}} & {\cdots} & {\boldsymbol{o}} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {\boldsymbol{O}} & {\boldsymbol{O}} & {\boldsymbol{o}} & {\boldsymbol{f}}\end{array}\right] $ | (4) |
T在这里表示两次连续测量时间之间采样的时间间隔,其中f为一个6阶矩阵,对应用户状态向量的6个分量,O为6阶的零矩阵,与f的维度相对应.用户i在t时刻的预测状态可由其在t-1时刻的坐标值和速度来推算,其预测状态表示为
| $ \left. \begin{array}{l} L x_{i}(t) &=L x_{i}(t-1)+V x_{i}(t-1) T \\ L y_{i}(t) &=L y_{i}(t-1)+V x_{i}(t-1) T \\ L z_{i}(t) &=L z_{i}(t-1)+V x_{i}(t-1) T \\ V x_{i}(t) &=V x_{i}(t-1) \\ V y_{i}(t) &=V y_{i}(t-1) \\ V z_{i}(t) &=V z_{i}(t-1) \end{array} \right\} $ | (5) |
在t时刻,待定位的用户测量方程可以表示为
| $ \mathit{\boldsymbol{Z}}(t) = h(\mathit{\boldsymbol{X}}(t)) + \mathit{\boldsymbol{N}}(t) $ | (6) |
其中:N(t)表示环境中的高斯白噪声;Z(t)是t时刻的测量值,也就是任意2个用户间距离的值和固定锚点和用户之间的值组成的向量.为了使其满足使用卡尔曼滤波的条件,这里取距离的平方构成新的测量方程:
| $ \begin{aligned} \boldsymbol{Z}(t)=&\left[D_{11}^{2}(t), \cdots, D_{i j}^{2}(t), D_{12}^{2}(t), \cdots,\right.\\ &\left.D_{j k}^{2}(t), \cdots, D_{n \times n-1}^{2}(t)\right] \end{aligned} $ | (7) |
其中:Djk2(t)表示的是用户j和用户k之间距离的平方,其中j, k=1, 2, …, n, 且j≠k,Dij2(t)表示的是固定锚点i和用户j之间距离的平方,其中i=1, 2, …, m; j=1, 2, …, n.他们可以分别通过式(8)和(9)求得,其中Axi、Ayi和Azi分别表示锚点i的x轴、y轴和z轴坐标(i=1, 2, …, m), Lxj(t)、Lyj(t)和Lzj(t)分别表示用户节点j在t时刻的x轴、y轴和z轴坐标(j =1, 2, …, n).
| $ \begin{array}{l}{D_{j k}(t)=|\left(\left(L x_{j}(t)-L x_{k}(t)\right)^{2}+\left(L y_{j}(t)-\right)\right.} \\ {\left.\left.L y_{k}(t)\right)^{2}+\left(L z_{j}(t)-L z_{k}(t)\right)^{2}\right)^{1 / 2}+N(t) |}\end{array} $ | (8) |
| $ \begin{aligned} D_{i j}(t)=& |\left(\left(L x_{j}(t)-A x_{i}\right)^{2}+\left(L y_{j}(t)-A y_{i}\right)^{2}+\right.\\ &\left.\left(L z_{j}(t)-A z_{i}\right)^{2}\right)^{1 / 2}+N(t) | \end{aligned} $ | (9) |
为了实现不断更新待定位用户实时位置的目标,基于扩展卡尔曼滤波移动群体算法需要循环执行.算法实现的具体步骤如下:首先输入锚点和待定位节点以及待定位节点之间的距离矩阵,并输入初始的预测误差和测量误差,根据第1节的公式分别计算预测误差方差和预测矩阵以及测量矩阵和预测矩阵的残差,此时就可以得到卡尔曼增益的值,并利用这个值计算最优的状态值.为了循环计算下一时刻的最优状态值,此时需要更新这一刻的误差协方差值,具体的算法描述如下.
算法1 基于扩展卡尔曼滤波的移动群体定位算法
输入:固定锚点和待定位节点以及待定位节点之间的距离
输出:待定位节点的坐标
1 初始化环境中用户的状态X_p(0),初始误差协方差P_p(0),预测误差Q和测量误差R
For t=1至T
2 根据式(2)预测待定位节点的状态向量X_p(t/t-1),并计算预测误差的方差P_p(t/t-1)=FP_p(t-1)FT+Q(t-1) //预测阶段
3 根据锚点的位置和未定位节点的预测状态计算预测矩阵h_Xp //更新阶段
4 计算测量值和预测值之间的测量残差Y_e
5 根据公式计算卡尔曼增益K(T)=P_p(t/t-1)H(HP_p(t-1)HT) -1
6 更新用户的状态,以得到t时刻的最优状态向量X_p(t)=X_p(t/t-1)+K(t)Y_e
7 为了使其不断循环,更新其此时在t时刻的误差协方差X_p(t)=X_p(t/t-1)+K(t)Y_e
8 End For;
2.2 算法分析假设有一个待定位群组(由3个位用户B1、B2和B3组成),3个用户分别在其中一个锚点的通信区域内,如图 1所示,且Bi和Ai的距离为di.如果用传统的定位方法无法定位出待定位用户的位置,但是用基于扩展卡尔曼滤波的移动群体定位算法能准确地定位用户的位置.
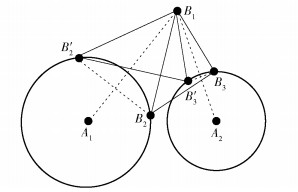
|
图 1 定位待定位用户示意图 |
证明 传统的定位方法是基于三边定位法,该方法的实现前提是必须知道某待定位节点和至少3个已知锚点间的距离信息,但题设条件是对于每个待定位用户,只知道它与其中一个锚点的距离(因为3位用户分别只在其中一个锚点的通信范围内,所以只能通过该锚点获取该用户的位置信息),显然不满足传统定位方法的条件,所以无法定位.
根据提出的方法可以实现精确定位的证明如下:
1) 当B1、B2满足条件dA1A2=d12+d1+d2或者dA1A2=d12-d1-d2时,可知B1、B2在直线A1A2上,故B1、B2能唯一确定.而此时的B3可以与B1、B2、A3进行通信,满足三边定位法的条件,所以它的位置也可以确定.
2) 当B1在A1A2上,则B1根据1)可知其位置唯一.而对于B2和B3,因为它们能与B1和A2,B1和A3分别通信,以B1为圆心,B1B2和B1B3的距离为半径画圆,其分别与圆A2、A3交于点B2和B′2,B′3和B′3,且B2B3≠B′2B′3,如图 1所示.所以在这种情况下用户的位置能唯一确定.
3) 当B1、B2都不在A1A2上时,如果B1的位置能唯一确定,由以上分析可知B2和B3的位置也能够唯一确定.所以,在这种情况下用户位置能唯一确定.
综上所述,使用传统定位方法不能实现准确定位,而提出的算法可以使处于题设条件下的3个待定位用户能够被准确定位.
算法时间复杂度分析:假设实验中存在n个待定位节点,因为每个节点的定位过程总共进行T次,而对于每个定位过程,时间复杂度为O(n),定位过程时间复杂度是O(T).则扩展卡尔曼滤波的时间复杂度是O(Tn).结果表明,提出的方法没有增加定位过程的复杂性.
3 实验 3.1 定位系统和实验环境设置为了进一步证明提出的定位方法能够在真实场景下进行准确定位,研制出了完整的定位系统.
实验环境的基本设置如下:选择的定位区域是一个20m×20m的正方形区域,4个固定节点放置在正方形的4个角的位置,作为已知的固定锚点,其中一个为协调器,负责传送数据到电脑. 3个待定位的节点分别沿着定位区域的边沿移动.
实验采用Visual Studio 2017和Matlab R2016b仿真软件,实验初始设置中预测误差Q为10-3,测试误差R为30,它们都是根据大量实验结果选取出定位结果最好的初值,即此时定位误差达到最小.
3.2 实验结果为了更好地体现所提算法的优越性,分别与Tri和EKF算法做了比较,其中Tri算法是基于固定锚点的三边定位方法,根据已知的3个及以上锚点和待定位节点的距离关系,使用三角几何原理确定待定位节点的方法;EKF为扩展卡尔曼滤波算法,只使用固定锚点的定位方法.图 4中的MEKF(mobile localization algorithm based on EKF)是指笔者提出的定位方法.
图 2给出了待定位节点3(由于几个节点的结果基本相同,只给出了一个结果)的定位结果,Tri算法得到的结果其稳定性不如MEKF方法,因为MEKF结果中两侧的分布更加均匀.相比于EKF方法,MEKF算法得到的定位数据更多,因为EKF方法在图中缺失了一部分数据.图中定位误差产生的原因如下:实验中采用的是CC2530节点,该节点虽然被广泛用于实验,但价格较为低廉,易受环境干扰,无线信号不稳定,导致某些节点之间的测量距离不准确,而测量距离是此定位方法的基础,因此会产生一定的误差,这是由硬件环境决定的.
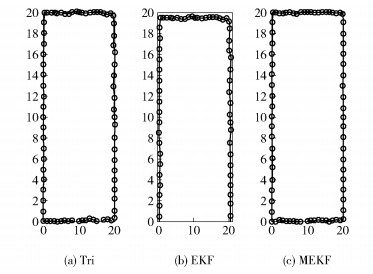
|
图 2 移动节点3的定位结果 |
如图 3所示,对于用户1~3,由定位方法MEKF得到的平均定位误差与Tri算法相比分别降低了40.8%、21.2%和54.7%,与EKF方法得到的平均定位误差相比分别降低了53.9%、18.8%和20.4%.
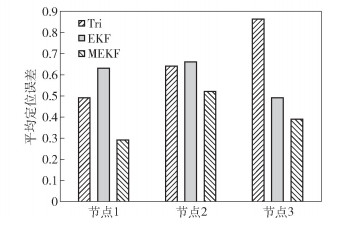
|
图 3 各节点平均定位误差 |
如图 4所示,当平均测距误差从0.5m增加到2.5m时,由定位方法MEKF得到的平均定位误差与Tri方法相比提高了34.2%~51.6%,与EKF方法相比提高了24.5%~37.7%.
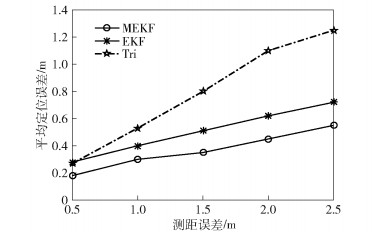
|
图 4 测距误差与平均定位误差的比较 |
如图 5所示,当用户之间的距离增加时,3种定位方法的平均定位误差都减小,这是因为当用户之间更接近时,待定位用户的信号会彼此干扰,导致待定位用户的平均定位误差增大.
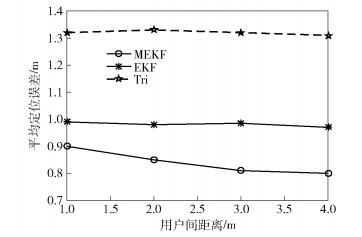
|
图 5 用户间距离与平均定位误差的比较 |
图 6所示的是随着丢失率增加,3种算法平均定位误差的变化情况.在实验中,通过删除一些收到的数据,控制删除的数据占总数据的比率从0~10%变化,结果显示,在丢包率相同的情况下,MEKF算法的平均定位误差均小于EKF算法.这是因为所提算法在缺失数据时,可以利用已经定位的节点的信息辅助定位待定位节点,从而弥补缺失数据带来的影响.
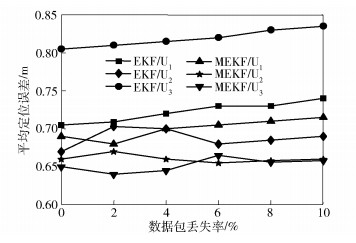
|
图 6 数据丢包率和平均定位误差的关系 |
利用了待定位节点之间的距离信息,提高了测量结果的容错率,也增加了实验结果的可靠性; 此外,使用的MEKF算法也在一定程度上削减了环境噪声等因素的影响.因此,笔者提出的基于卡尔曼滤波的移动群体无线定位方法相比于传统的算法可以实现更高精度的定位,且它可以得到更加稳定的定位效果.
4 结束语近年来,在万物互联的背景下,无线定位技术被广泛应用于军事、农业、消防等诸多领域.如何能提高定位的准确度,从而更好地满足人们的需求是无线定位技术发展亟待解决的问题.笔者提出的基于扩展卡尔曼滤波的移动群体定位方法,合理地利用了环境中移动的待定位节点之间的距离信息,提高了定位的精度,降低了节点定位误差.结合改进的扩展卡尔曼滤波算法,减小了环境噪声等因素的影响,可以进一步提高定位的精度.实际系统测试结果说明,提出的基于扩展卡尔曼滤波的移动群体定位方法比传统定位方法的定位精度提高了30%左右,可以作为未来无线定位的有效选择方案.
| [1] |
Wang T, Peng Z, Liang J, et al. Following targets for mobile tracking in wireless sensor networks[J]. ACM Transactions on Sensor Networks (TOSN), 2016, 12(4): 31-55. |
| [2] |
Tsai M F, Wang P C, Shieh C K, et al. Improving positioning accuracy for VANET in real city environments[J]. The Journal of Supercomputing, 2015, 71(6): 1975-1995. DOI:10.1007/s11227-014-1215-9 |
| [3] |
王文华, 王田, 吴群, 等. 传感网中时延受限的移动式数据收集方法综述[J]. 计算机研究与发展, 2017, 54(3): 474-492. Wang Wenhua, Wang Tian, Wu Qun, et al. Survey of delay-constrained data collection with mobile elements in WSNs[J]. Journal of Computer Research and Development, 2017, 54(3): 474-492. |
| [4] |
Wu C, Yang Z, Xu Y, et al. Human mobility enhances global positioning accuracy for mobile phone localization[J]. IEEE Transactions on Parallel and Distributed Systems, 2015, 26(1): 131-141. DOI:10.1109/TPDS.2014.2308225 |
| [5] |
Villalpando-Hernández R, Muñoz-Rodríguez D, Vargas-Rosales C, et al. 3-D position location in Ad Hoc networks:a manhattanized space[J]. IEEE Communications Letters, 2017, 21(1): 124-127. DOI:10.1109/LCOMM.2016.2613082 |
| [6] |
Dang Xiaochao, Hei Yilin, Hao Zhanjun. An improved indoor localization based on RSSI and feedback correction of anchor node for WSN[C]//2016 International Conference on Computer, Information and Telecommunication Systems (CITS). Yunnan China: IEEE, 2016: 1-5.
|
| [7] |
王田, 梁玉珠, 彭臻, 等. 无线传感器网络中移动目标探测跟踪研究进展[J]. 软件学报, 2017, 28(s1): 115-128. Wang Tian, Liang Yuzhu, Peng Zhen, et al. Research advance of detection-centric target tracking with mobile elements in wireless sensor networks[J]. Journal of Software, 2017, 28(s1): 115-128. |
| [8] |
Deng Z A, Hu Y, Yu J, et al. Extended Kalman filter for real time indoor localization by fusing WiFi and smartphone inertial sensors[J]. Micromachines, 2015, 6(4): 523-543. DOI:10.3390/mi6040523 |
| [9] |
Wang T, Wang W, Cao J, et al. Interoperable localization for mobile group users[J]. Computer Communications, 2017(105): 53-65. |
| [10] |
王国军, 王田, 贾维嘉. 无线传感器网络中一种基于行进启发的地理位置路由[J]. 传感技术学报, 2007, 20(2): 382-386. Wang Guojun, Wang Tian, Jia Weijia. March inspired geographic routing protocol in wireless sensor networks[J]. Chinese Journal of Sensors and Actuators, 2007, 20(2): 382-386. DOI:10.3969/j.issn.1004-1699.2007.02.033 |
| [11] |
王田, 张广学, 蔡绍滨, 等. 传感云中的信任评价机制研究进展[J]. 通信学报, 2018, 39(6): 37-51. Wang Tian, Zhang Guangxue, Cai Shaobin, et al. Survey on trust evaluation mechanism in sensor-cloud[J]. Journal on Communications, 2018, 39(6): 37-51. |
| [12] |
何异舟, 崔高峰, 李鹏旭, 等. 卫星移动终端增强型卡尔曼滤波协同自主定位算法[J]. 北京邮电大学学报, 2015, 38(3): 94-98. He Yizhou, Cui Gaofeng, Li Pengxu, et al. A satellite mobile terminals cooperative autonomous positioning algorithm based on enhanced kalman filter[J]. Journal of Beijing University of Posts and Telecommunications, 2015, 38(3): 94-98. |
| [13] |
Wang Tian, Xing Guoliang, Li Minming, et al. Efficient wifi deployment algorithms based on realistic mobility characteristics[C]//The 7th IEEE International Conference on Mobile Ad-hoc and Sensor Systems (IEEE MASS 2010). San Francisco: IEEE, 2010: 422-431.
|



