第5代移动通信系统(5G)子带滤波正交频分复用技术(F-OFDM)存在较高峰均功率比(PAPR)问题,传统选择性映射算法候选序列数量少,对此,提出量子混沌扩展序列算法,以解决5G F-OFDM系统PAPR较高的问题.采用分割方法将原始信号分割为实部信号和虚部信号,用量子Logistic混沌映射分别与实部信号和虚部信号进行点乘,实部候选序列与虚部候选序列线性组合后再计算PAPR,选择最小PAPR进行传输.仿真结果表明,提出的算法降低了系统的PAPR,扩展了候选序列数量,降低了计算复杂度.
High peak to average power ratio (PAPR) is a main problem of the fifth generation of mobile communications system(5G) filtered-orthogonal frequency division multiplexing (F-OFDM) systems. Aiming at the shortcomings of traditional selective mapping algorithm, such as limited number of candidate sequences, the quantum chaotic extended sequence algorithm was proposed to solve the high PAPR problem of 5G F-OFDM systems. The original signal was divided into real part signal and imaginary part signal by segmentation method, which were respectively multiplied the quantum logistic chaotic map. The PAPR was calculated by linear superposition of real sequences and the imaginary part candidate, and the minimum PAPR was selected for transmission. The simulation results show that the proposed algorithm reduces the PAPR of 5G F-OFDM system, increases the number of candidate signals and reduces the computational complexity. The proposed scheme has a broad application prospect in 5G multicarrier modulation technology.
传统的正交频分复用(OFDM,orthogonal frequency division multiplexing)技术无法满足第5代移动通信系统(5G)海量连接的需求[1].为了解决5G各种应用场景和多样性的业务需求问题,学者们提出了适合5G的新型多载波技术[2-4].子带滤波正交频分复用技术(filtered-OFDM)将系统带宽划分为多个子带,子载波映射模块为各子带的子载波编号. F-OFDM子带符号的频谱有一定重叠,在实现中,为了避免F-OFDM子带上的OFDM信号通过数模转换器时引起混淆,需要过采样,使系统产生较高峰均功率比(PAPR,peak to average power ratio)[5].
扰码技术是一种降低PAPR的主要方法,其中,选择性映射(SLM,selective mapping)算法结构简单、明了,效果显著,但运算复杂度较高,许多研究人员对SLM算法进行了改良[6-10].
笔者提出量子混沌扩展序列算法,旨在降低5G F-OFDM系统较高的PAPR.采用量子混沌序列代替传统伪随机序列,作为随机相位序列矢量,满足5G海量连接的需求.
1 F-OFDM系统分析F-OFDM是基于子带滤波的OFDM,将系统带宽划分为若干子带,每种子带根据不同业务场景需求配置不同的子载波带宽和循环前缀(CP,cycle prefix),从而满足不同业务的时频资源需求.各子带上含有对子带进行滤波的子带滤波器,从而降低子带带外频谱泄露,F-OFDM收发机架构如图 1所示.
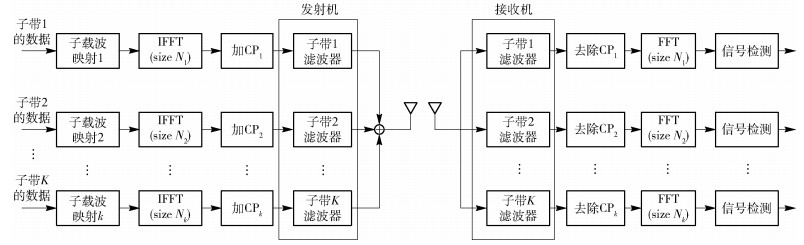
|
图 1 F-OFDM收发机架构示意图 |
时间离散的F-OFDM子带OFDM信号为
| $ x(n)=\sum\limits_{m=0}^{N_{s}-1} X(m) \mathrm{e}^{\mathrm{j} 2 \pi \frac{m n}{N}} $ | (1) |
其中:用N个采样点表示连续时间周期为T的FOFDM子带OFDM信号,m/N表示第m个子载波的频率,n表示子载波编号,Ns表示子载波数量,N>Ns.
式(1)的复包络为
| $ A(t) = x(t){\rm{ + j }}y(t) $ | (2) |
F-OFDM输入的串行数据一帧为M bit,每帧分为N组,第i组有Li bit.
| $ M=\sum\limits_{i=1}^{N} L_{i} $ | (3) |
第i组比特对应第i个子信道的信号dn(n=0, 1, …, N-1),通过IFFT完成{dn}的F-OFDM基带调制,则F-OFDM信号为
| $ \begin{array}{l} f(t) = {\mathop{\rm Re}\nolimits} \{ A(t)\left. {{{\rm{e}}^{{\rm{j}}{\omega _0}t}}} \right\} = \\ {\mathop{\rm Re}\nolimits} \left\{ {(x(t) + {\rm{j}}y(t))\left( {\cos {\omega _0}t + {\rm{j}}\sin {\omega _0}t} \right)} \right\} = \\ x(t)\cos {\omega _0}t - y(t)\sin {\omega _0}t \end{array} $ | (4) |
F-OFDM系统与OFDM系统区别在于增加了子带滤波功能,子带滤波器冲激响应为h(n),则其输出信号为
| $ w(n)=f(n) h(n) $ | (5) |
耗散量子系统通常被描述为将系统耦合到谐振子的路径上,以构造具有量子校正的量子Logistic映射. Akhshani等[11]证明了非常低阶的量子校正可以产生下述混沌映射:
| $ {\phi _2}\left( {x_n^\prime } \right) = r\left( {x_n^\prime - {{\left| {x_n^\prime } \right|}^2}} \right) - ry_n^\prime $ | (6a) |
| $ \begin{array}{l} {\phi _2}\left( {y_n^\prime } \right) = - y_n^\prime {{\rm{e}}^{ - 2\beta }} + {{\rm{e}}^{ - \beta }}r\left[ {\left( {2 - x_n^\prime - x_n^{\prime *}} \right)y_n^\prime - } \right.\\ \left. {x_n^\prime z_n^{\prime *} - x_n^{\prime *}z_n^\prime } \right] \end{array} $ | (6b) |
| $ \phi_{2}\left(z_{n}^{\prime}\right)=-z_{n}^{\prime} \mathrm{e}^{-2 \beta}+\mathrm{e}^{-\beta} r\left[2\left(1-x_{n}^{\prime *}\right) z_{n}^{\prime}-2 x_{n}^{\prime} y_{n}^{\prime}-x_{n}^{\prime}\right] $ | (6c) |
其中:r为可调参数,β为耗散参数,x′n*为x′n的复共轭,z′n*为z′n的复共轭.
通过式(6)生成量子Logistic映射,具有自然并行性、结构简单、容量大、不易破解等优点,能够满足5G海量用户的需求.
2.2 量子混沌扩展序列算法分析针对传统SLM算法候选序列数量少的缺点,提出了量子混沌扩展序列(QCES,quantum chaotic extended sequence)算法,采用分割方法将原始信号分割为实部信号和虚部信号,并采用量子Logistic混沌映射代替传统伪随机序列作为随机相位序列矢量分别与实部信号和虚部信号进行点乘,然后进行IFFT变换,实部候选序列与虚部候选序列组合后计算PAPR,选择最小PAPR进行传输.
如图 2所示,5G F-OFDM数据块为x(t),对串行输入的信号x(t)进行符号映射,通过串并变换分成2N个子信道,采用分割方法将信号x(t)分割为实部和虚部,分别在N个子信道上进行传输.采用量子Logistic混沌映射生成N个不同的长度为M的随机相位序列矢量P,则第m个随机相位序列矢量为Pm=(Pm, 0, Pm, 1, …, Pm, M-1), 0≤m≤N-1.第u个数据块xu(t)分割为实部xu_r(t)和虚部xu_i(t),分别与第m个随机相位序列矢量Pm点乘,然后进行IFFT运算,分别产生候选传输序列su_rm(t)、su_im(t).
| $ \begin{array}{l} s_{u\_{\rm{r}}}^m(t) = {\mathop{\rm IFFT}\nolimits} \left( {{x_{u\_{\rm{r}}}}(t) \otimes {P_m}} \right) = \\ {\mathop{\rm IFFT}\nolimits} \left( {{x_{u\_{\rm{r, 0}}}}(t){P_{m, 0}}, {x_{u\_{\rm{r, 1}}}}(t){P_{m, 1}}, \cdots } \right., \\ \left. {{x_{u\_{\rm{r}}, N - 1}}(t){P_{m, M - 1}}} \right), 0 \le m \le N - 1 \end{array} $ | (7) |
| $ \begin{array}{l} s_{u\_{\rm{i}}}^m(t) = {\mathop{\rm IFFT}\nolimits} \left( {{x_{u\_{\rm{i}}}}(t) \otimes {P_m}} \right) = \\ {\mathop{\rm IFFT}\nolimits} \left( {{x_{u\_{\rm{i}}{\rm{, 0}}}}(t){P_{m, 0}}, {x_{u\_{\rm{i}}{\rm{, 1}}}}(t){P_{m, 1}}, \cdots } \right., \\ \left. {{x_{u\_{\rm{i}}, N - 1}}(t){P_{m, M - 1}}} \right), 0 \le m \le N - 1 \end{array} $ | (8) |
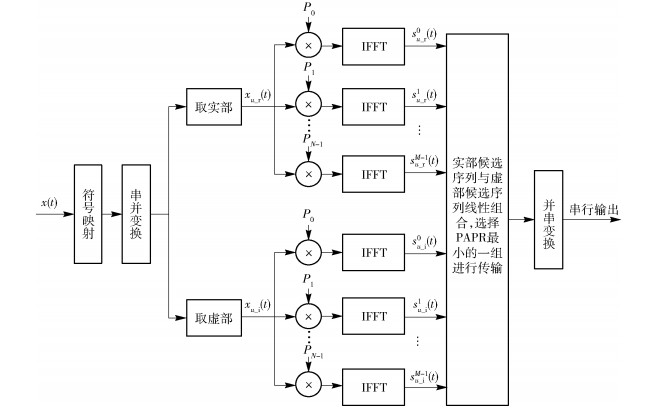
|
图 2 量子混沌扩展序列算法的原理图 |
其中:su_rm(t)为实部候选序列,su_im(t)为虚部候选序列.
实部的候选序列su_rk(t)和虚部的候选序列su_iq(t)进行线性组合,αk、βg均为系数,得到候选传输序列suk, q(t)为
| $ \begin{array}{*{20}{c}} {s_u^{k, q}(t) = {\alpha _k}s_{u\_{\rm{r}}}^k(t) \pm {\rm{j}}{\beta _g}s_{{u_ - }{\rm{i}}}^q(t) = }\\ {{\alpha _k}{\mathop{\rm IFFT}\nolimits} \left( {{x_{{u_ - }{\rm{r}}}}(t) \otimes {P_k}} \right) \pm {\rm{j}}{\beta _g}{\mathop{\rm IFFT}\nolimits} \left( {{x_{u\_i}}(t) \otimes {P_q}} \right)} \end{array} $ | (9) |
扩展后的候选传输序列seu(t)表示为
| $ \begin{array}{c}{s_{e u}(t)=\left\{s_{u}^{0}(t), s_{u}^{1}(t), \cdots, s_{u}^{n}(t), \cdots, s_{u}^{N^{2}-1}(t)\right\}}, \\ {0 \leqslant n \leqslant N^{2}-1}\end{array} $ | (10) |
选择第u个数据块候选传输序列中PAPR最小的一组记为Xu,则
| $ {X_u} = \mathop {\arg \min }\limits_{0 \le n \le {N^2} - 1} \left\{ {{\mathop{\rm PAPR}\nolimits} \left( {s_u^n(t)} \right)} \right\}, 0 \le u \le N - 1 $ | (11) |
故输出序列为
| $ X = \sum\limits_{u - 0}^{N - 1} {{X_u}} $ | (12) |
笔者采用QPSK调制,子载波数为128,用互补累积分布函数(CCDF,complementary cumulative distribution function)来描述系统PAPR的分布情况. Moon等[12]提出了选定数据方法(SDU,selected data utilization),给定特定的选择条件来旋转相位因子,从而对传统SLM算法的PAPR性能进行改进.笔者提出的量子混沌扩展序列算法与传统SLM算法和SDU算法的PAPR性能比较如图 3所示.
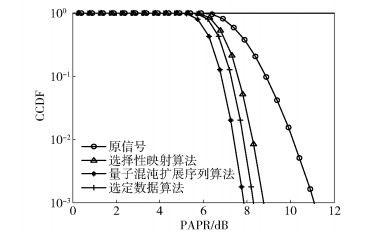
|
图 3 不同算法下的PAPR性能对比 |
从图 3可以看出,与传统SLM算法和SDU算法相比,笔者提出的量子混沌扩展序列算法更加有效地降低了系统的PAPR.
假设传统SLM算法和笔者提出的量子混沌扩展序列算法均产生L2个候选序列,子载波数为R,过采样率为Q,RQ点的IFFT变换需要进行
当候选序列为L2时,笔者提出的量子混沌扩展序列算法与传统的SLM算法计算复杂度比较如表 1所示.
|
|
表 1 不同算法下的计算复杂度对比 |
由表 1可知,当候选序列均为L2时,所提出的量子混沌扩展序列算法需要的复数乘法次数为传统SLM算法的
对传统的SLM算法进行了改进,提出了量子混沌扩展序列算法,解决了5G F-OFDM系统的高PAPR问题.面向5G海量连接需求,采用量子混沌序列代替传统伪随机序列,可提供大量随机相位序列矢量.采用分割方法,扩展了候选序列数量,降低了计算复杂度,提高了传输效率,在5G多载波调制技术中具有一定的应用价值.
| [1] |
钱孟娇. 5G移动通信系统中F-OFDM关键技术的研究[D].西安: 西安科技大学, 2018. http://cdmd.cnki.com.cn/Article/CDMD-10357-1018123123.htm
|
| [2] |
Liu Ling, Zhou Yiqing, Garcia V, et al. Load aware joint CoMP clustering and inter-cell resource scheduling in heterogeneous ultra dense cellular networks[J]. IEEE Transactions on Vehicular Technology, 2018, 67(3): 2741-2755. DOI:10.1109/TVT.2017.2773640 |
| [3] |
Garica V, Zhou Yiqing, Shi Jinglin. Coordinated multi point transmission in dense cellular networks with user-centric adaptive clustering[J]. IEEE Transactions on Wireless Communications, 2014, 13(8): 4297-4308. DOI:10.1109/TWC.2014.2316500 |
| [4] |
Bi Meihua, Jia Weikang, Li Longsheng, et al. Load diversity based optimal processing resource allocation for super base stations in centralized radio access networks[C]//2014 IEEE International Conference on Communications (ICC). New York: IEEE Press, 2014: 5119-5124.
|
| [5] |
杨立章. F-OFDM系统中子带滤波器的设计及PAPR抑制方法的研究[D].合肥: 安徽大学, 2018. http://cdmd.cnki.com.cn/Article/CDMD-10357-1018123123.htm
|
| [6] |
Xiao Yaoqiang, Wang Zhiyi, Cao Jun, et al. Time-frequency domain encryption with SLM scheme for physical-layer security in an OFDM-PON system[J]. Journal of Optical Communications and Networking, 2018, 10(1): 46-51. DOI:10.1364/JOCN.10.000046 |
| [7] |
Hu Weiwen. SLM-based ACO-OFDM VLC system with low-complexity minimum amplitude difference decoder[J]. Electronics Letters, 2018, 54(3): 144-146. DOI:10.1049/el.2017.3158 |
| [8] |
胡武君, 杨霖. MIMO-OFDM系统中基于循环移位和信号联合的改进SLM算法[J]. 通信学报, 2015, 36(4): 1-8. HU Wujun, YANG Lin. Modified SLM algorithm based on cyclic shift and signal combination in MIMO-OFDM system[J]. Journal on Communications, 2015, 36(4): 1-8. DOI:10.3969/j.issn.1001-2400.2015.04.001 |
| [9] |
Sudha V, Syamkumar M, Kumar D S. A low complexity modified SLM and companding based PAPR reduction in localized OFDMA[J]. Wireless Personal Communications, 2017, 96(2): 3207-3226. |
| [10] |
Yuan Jianguo, Shen Qian, Wang Jingxin, et al. A novel improved SLM scheme of the PAPR reduction technology in CO-OFDM systems[J]. Optoelectronics Letters, 2017, 13(2): 138-142. DOI:10.1007/s11801-017-6265-9 |
| [11] |
Akhshani A, Akhavan A, Lim S C, et al. An image encryption scheme based on quantum logistic map[J]. Communications in Nonlinear Science and Numerical Simulation, 2012, 17(12): 4653-4661. DOI:10.1016/j.cnsns.2012.05.033 |
| [12] |
Moon J H, Nam Y R, Choi E J, et al. Selected data utilization technique for the PAPR reduction of FBMC-OQAM signals[C]//2017 Ninth International Conference on Ubiquitous and Future Networks (ICUFN). New York: IEEE Press, 2017: 741-743.
|


