为了克服传统语音端点检测算法在低信噪比环境下准确率低的问题,提出一种基于谱熵梅尔积(MFPH)的语音端点检测算法.首先,提取带噪语音信号的梅尔频率倒谱系数中的第一维参数MFCC0,将其与谱熵的乘积作为最终区分语音段和背景噪声段的融合特征参数;然后,结合模糊C均值聚类算法和贝叶斯信息准则(BIC)算法对MFPH特征参数门限值进行自适应估计;最后,采用双门限法进行语音端点检测.实验结果证明,与传统方法比较,该方法在-5~15 dB低信噪比环境下的语音端点检测准确率有较大提高.
In order to solve the problem that the accuracy of traditional voice activity detection algorithms is low in the low signal-to-noise ratio (SNR) environment, a voice activity detection algorithm based on product of spectral entropy and Mel (MFPH) was proposed. Firstly, the first dimensional parameter MFCC0 of Mel frequency spectrum coefficient of the speech signal with noisy was extracted, and the product of MFCC0 and spectral entropy was taken as fusion characteristic parameter of finally distinguishing speech segment from background noise. Then, the threshold value of MFPH characteristic parameters was estimated adaptively based on combination of fuzzy C-means clustering algorithm (FCM) and Bayesian information criterion (BIC). Finally, the double-threshold method was adopted for the voice activity detection. Experiments show that the accuracy of the proposed method is greatly improved in the -5~15 dB low SNR environment compared with traditional methods.
语音端点检测本质上是寻找能区别语音段和背景噪声段的特征参数对语音段和背景噪声段进行准确划分的方法[1].优秀的语音端点检测方法能降低检测时间、适应恶劣的噪声环境、提高准确率.语音信号端点检测的性能能决定一个语音识别系统的成败[2].
语音端点检测起源于20世纪50、60年代,由Bell实验室提出并经历了快速的发展,国内外学者提出了上百种优秀的算法.一类是基于模式识别的算法[3],张毅等[4]提出一种基于模糊熵与改进相关向量机的端点检测算法,在低信噪比环境下准确率达到了93.2%;Kim等[5]提出基于RBF神经网络算法的语音端点检测方法在不同噪声水平下都比传统算法检测精度高.虽然这类算法的准确率高,但是计算复杂,运算量大,实时性无法保证.另一类是基于语音信号的某个特征的方法,比如传统谱熵(SE,spectral entropy)法、短时能量、自相关法等,这类算法计算量小,实时性高,但是无法适应低信噪比(SNR,signal-to-noise ratio)的环境.对此,国内外学者提出了大量的多特征结合的算法,这类算法同时具有较高的实时性和低信噪比环境下的检测准确率.如张晓雷等[6]提出一种由2个子特征加权构成一种多观测复合特征(MO-CF,muitiple observation compound feature)用于语音端点检测,在多种噪声环境下比传统端点检测方法的稳健性更高;胡波等[7]将语音端点检测和基音提取的步骤合二为一,提高了识别的准确率,降低了系统的复杂度.这些方法在低SNR环境下都取得了较好的检测效果.
梅尔频率倒谱系数(MFCC,Mel frequency cepstrum coefficient)中的第一维参数(MFCC0)比MFCC中其他分量大得多,用来做特征参数时,会影响其他分量在语音识别中的作用,但是研究发现,MFCC0对语音有较好的跟踪能力, MFCC0在有声段的值远远大于无声段的值.另一方面,虽然SE本身具有一定的抗噪性能,但是依然无法满足实际语音识别系统的要求.为了提高低信噪比环境下语音端点的检测准确率,将MFCC0与SE的乘积作为语音端点检测的特征参数.对于门限值估计,采用贝叶斯信息准则和模糊C均值聚类算法结合,实现门限值随噪声改变自适应更新.仿真实验证明,在噪声环境下端点检测效果明显优于传统端点检测算法.
1 参数MFCC0提取 1.1 MFCC为了提高语音的识别率,Davis等[8]于1980年首次提出了着眼于人耳的听觉特性[1]的MFCC.声道的形状表现在短时间功率谱包络,MFCC的作用是准确地代表这个包络.所以相对于其他特征参数,MFCC在低信噪比环境下检测语音端点效果更佳[9].
1.2 计算MFCC01) 时域语音信号x(t)加窗分帧后进行快速傅里叶变换(FFT,fast Fourier transform)处理, 得到每一帧语音频域信号:
| $ X(i,k) = {\rm{FFT}}\left[ {{x_i}(r)} \right] $ | (1) |
其中:i表示第i帧,k表示第k条谱线,r表示第r个采样点.
2) 计算每一帧能量谱:
| $ E(i,k) = {[X(i,k)]^2} $ | (2) |
3) 对能量谱应用梅尔滤波器组,对通过每一个滤波器的能量求和.
| $ S(i,m) = \sum\limits_{k = 0}^{N - 1} E (i,k){H_m}(k),\;\;\;\;\;0 \le m \le M $ | (3) |
其中:Hm(k)表示带通三角形滤波器,M表示滤波器个数,m表示第m个滤波器.
4) 对能量的对数做离散余弦变换(DCT,discrete cosine transform),即得MFCC参数:
| $ \begin{array}{*{20}{c}} {{\rm{mfcc}}(i,n) = }\\ {\sqrt {\frac{2}{M}} \sum\limits_{m = 0}^{M - 1} {\log } [S(i,m)]\cos \left[ {\frac{{{\rm{ \mathsf{ π} }}n(2m - 1)}}{{2M}}} \right]} \end{array} $ | (4) |
其中n是DCT后的谱线.
5) 去除MFCC首位各两帧数据,然后取每一帧MFCC系数的第1个数,组成新的特征参数MFCC0.
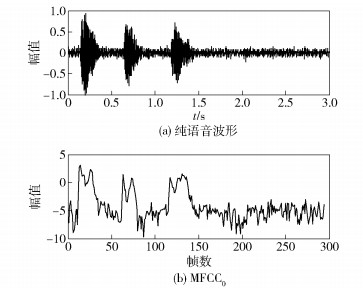
图 1是纯净语音信号的MFCC0特征波形图.
|
图 1 纯净语音信号的MFCC0特征 |
Mcclellan等[10]首次将SE引入语音端点检测中,实际上是检测谱的平坦程度.但是在无噪声和低信噪比环境下,SE的端点检测方法效果很差,准确率大大下降[11]. SE的计算包括2个步骤.
1) 时域语音信号x(t)经加窗分帧和FFT变换后, 其中第k条谱线频率分量fk的能量谱为Yi(k),则每个频率分量的归一化谱概率密度函数定义为
| $ {P_i}(k) = \frac{{{Y_i}(k)}}{{\sum\limits_{l = 0}^{N/2} {{Y_i}} (l)}} $ | (5) |
其中: Pi(k)为第i帧第k个频率分量fk对应的概率密度,N为FFT长度.
2) 第i帧的谱熵H(i)表示为
| $ H(i) = - \sum\limits_{n = 0}^{N/2} {{P_i}} (k)\lg \left[ {{P_i}(k)} \right] $ | (6) |
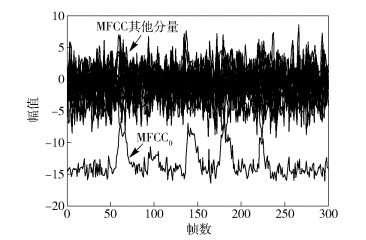
图 2所示为一段纯净语音信号MFCC各分量的对比.可以看出,MFCC参数的第一维参数MFCC0比其他分量大得多,所以MFCC用来做特征参数时,MFCC0会影响其他分量在语音识别中的作用.但是同时发现,MFCC0对语音有较好的跟踪能力, MFCC0在有声段的值远远大于无声段的值,所以可以将MFCC0应用在语音端点检测上. MFCC0是在MFCC参数中提取出来的,如同MFCC参数一样,在高信噪比环境下表现良好,但是在低信噪比环境下却不能很好地追踪语音.
|
图 2 纯净语音信号MFCC参数各分量的对比 |
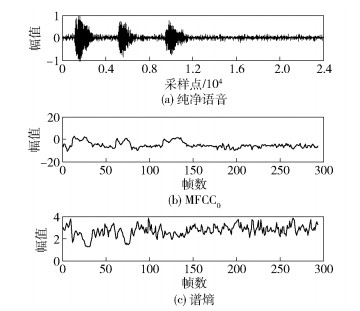
图 3所示为“five, six, seven”纯净语音的MFCC0参数和SE参数的表现情况,可以看出,SE在无噪声情况下对噪声的跟踪效果不尽人意[11],比MFCC0差很多,在有噪声环境下的检测效果相对稳定.
|
图 3 纯净语音信号的MFCC0和谱熵参数的对比 |
MFCC0特征参数是在MFCC的基础上提取出来的,MFCC本身对噪声的鲁棒性比较好,可考虑把2个参数结合成一个新的特征参数.因为谱熵有声段小于无声段,并且是正值,取相反数后有声段大于无声段,并且都是负值. MFCC0参数同样呈现这样的特性,所以将MFCC0参数与谱熵的负数相乘,那么无声段和有声段的数值差会更大,对语音的跟踪效果会更好,将此参数取名谱熵梅尔积(MFPH,product of spectral entropy and Mel).
因为要与MFCC0相乘,而MFCC0参数去除了MFCC的首尾各两帧,所以谱熵值也要去除首尾各2帧才能与MFCC0维数相等. MFPH的计算公式如
| $ M(i) = - {M_0}(i)H(i) $ | (7) |
其中:M(i)表示第i帧的MFPH值,M0(i)表示第i帧的MFCC0值.
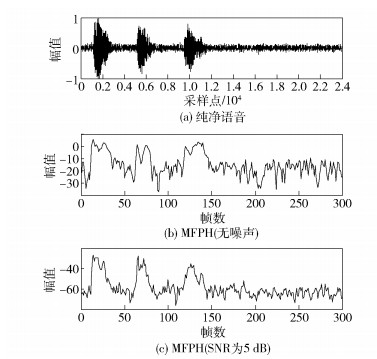
图 4所示为一段语音在无噪声情况下和信噪比为5dB的白噪声下的MFPH参数波形.可以看出,无噪声的MFPH参数在图上显示虽然有些凌乱,但是相对纯净语音的谱熵值来说,特征比较明显,语音段大于无声段.信噪比为5dB白噪声情况下,MFPH参数把噪声信号段和语音信号段区分得很明显,语音段的MFPH参数大于非语音段的MFPH参数,具有低信噪比情况下的语音端点检测能力.
|
图 4 语音信号的MFPH参数 |
门限估计与端点检测算法采用Tian等[12]提出的模糊C均值聚类算法和贝叶斯信息准则结合的算法进行门限值估计,再采用双门限法进行语音端点检测.该算法对估计的时间间隔不敏感,并且对环境变化有快速追踪能力.
4.1 模糊C均值聚类算法模糊C均值聚类是近30年聚类算法中较为经典和常用的传统聚类算法,能够获取全局最优解[13],算法如下.
假设有N个数据组成的样本集合X={x1, x1, …, xN}, C是聚类的类别数,第i类聚类中心为mi,模糊C均值聚类算法的最终目标是使式(8)结果最小.
| $ J = \sum\limits_{j = 1}^C {\sum\limits_{i = 1}^N {{{\left[ {{\mu _j}\left( {{x_i}} \right)} \right]}^b}} } {\left\| {{x_j} - {m_j}} \right\|^2} $ | (8) |
其中: μj(xi)表示样本数据Xi属于第j类的隶属度函数; b为模糊常数,并且b>1.
隶属度函数满足
| $ \sum\limits_{j = 1}^C {{\mu _j}\left( {{x_i}} \right) = 1} $ | (9) |
要使式(8)中J最小,可以分别对mj和μj(xi)求偏导,使其结果为0,则可以求出J的极小值.可得
| $ {m_j} = \frac{{\sum\limits_{i = 1}^N {{{\left[ {{\mu _j}{x_i}} \right]}^b}} {x_i}}}{{\sum\limits_{i = 1}^N {{{\left[ {{\mu _j}{x_i}} \right]}^b}} }} $ | (10) |
| $ {\mu _j}\left( {{x_i}} \right) = \frac{{{{\left( {\frac{1}{{{{\left\| {{x_i} - {m_j}} \right\|}^2}}}} \right)}^{1/b - 1}}}}{{\sum\limits_{k = 1}^C {{{\left( {\frac{1}{{{{\left\| {{x_i} - {m_j}} \right\|}^2}}}} \right)}^{1/b - 1}}} }},i = 1,2, \cdots ,C $ | (11) |
模糊C均值聚类算法步骤:
1) 初始化聚类类别数C和模糊参数b;
2) 初始化聚类中心;
3) 使用聚类中心mj计算隶属度函数μj(xi),再利用算出的μj(xi)计算出新的mj;
4) 重复步骤3),直到各样本数据的隶属度函数值趋于稳定.
4.2 贝叶斯信息准则在语音端点检测时,需要判断是否只有背景噪声或者含有语音段,
这时候就需要判断最优的聚类数目.贝叶斯信息准则常被用于确定分类器的分类数目[14].
贝叶斯信息准则的定义公式如下:
| $ {\rm{BIC}}(M) = \log L(X,\mathit{\Phi }) - {\gamma _p}\frac{1}{2}{n_\mathit{\Phi }}\log N $ | (12) |
其中:X={X1, X2, …, XN}为模型建立的数据样本,Φ={Φ1, Φ2, …, ΦN}为模型参数,L(X, Φ)为X和Φ的似然函数,nΦ为模型参数的数量,N为样本数据的个数,γp为模型参数数目的惩罚项.
最优的聚类数目C是使BIC值最大的值.假设背景噪声和语音都服从高斯分布N(μi, εi),聚类数目为C时的BIC可由下式确定:
| $ \begin{array}{*{20}{c}} {{\rm{BIC}}(C) = \sum\limits_{i = 1}^C {\left( { - \frac{1}{2}{N_i}\log \left| {{\varepsilon _i}} \right|} \right)} - }\\ {\frac{{\log N}}{2}{\gamma _p}C\left[ {d + \frac{{d(d + 1)}}{2}} \right]} \end{array} $ | (13) |
其中:N为总的样本数量,Ni为属于第i类的样本数量, d为特征空间的维数.
对于语音端点检测,最优聚类数目可由式(14)判断:
| $ {C_{{\rm{best}}}} = \left\{ {\begin{array}{*{20}{l}} {1,}&{{\rm{BIC}}(1) > {\rm{BIC}}(2)}\\ {2,}&{其他} \end{array}} \right. $ | (14) |
通过模糊C均值聚类算法和贝叶斯信息准则结合对双门限法的门限值进行自适应估计,并进行端点检测,具体步骤如下:
1) 通过式(7)计算MFPH;
2) 利用FCMC计算在特征MFPH下的聚类为C=1和C=2时的聚类中心,分别为m11和[m21,m22];
3) 根据式(14)判断最佳聚类数目Cbest;
4) 若Cbest=1, 则门限值满足:
| $ \left. {\begin{array}{*{20}{l}} {{T_{\rm{h}}} = {m_{11}} + {\beta _{\rm{h}}}}\\ {{T_1} = {m_{11}} + {\beta _1}} \end{array}} \right\} $ | (15) |
否则
| $ \left. {\begin{array}{*{20}{l}} {{M_{{\rm{voice}}}} = \max \left( {{m_{21}},{m_{22}}} \right)}\\ {{M_{{\rm{noise}}}} = \min \left( {{m_{21}},{m_{22}}} \right)} \end{array}} \right\} $ | (16) |
| $ \left. {\begin{array}{*{20}{l}} {{T_{\rm{h}}} = {M_{{\rm{voice}}}} + {\gamma _{\rm{h}}}}\\ {{T_1} = {M_{{\rm{noise}}}} + {\gamma _1}} \end{array}} \right\} $ | (17) |
其中:Th和Tl分别为双门限法中高低门限值,βh、βl、γh、γl为经验常数.
5) 根据双门限法找出语音端点.
5 实验验证与分析 5.1 实验设计仿真实验所采用的语音信号选自NUST603_2014及TIMIT语音库,噪声样本选自NOISE_92噪声库.
实验平台:联想笔记本电脑(CPU: Intel(R) Core(TM) i5-7300HQ; 显卡: GTX1050; RAM: 8G; Windows: Windows10, 64位操作系统),仿真软件:Matlab R2014a.
随机从NUST603_2014语音库和TIMIT分别选择50条语音,每条语音又分别与白噪声、粉噪声和汽车噪声混合成信噪比为-5、0、5、10dB的带噪语音,这样就产生了1200条测试语音.
测试了所提出的算法在不同信噪比环境下端点检测的准确率,并与传统语音端点算法进行比较.选择的传统算法有短时过零率法(ZCR,short-time zero-crossing rate method)、SE法、能零比法(EZR,short-time energy-zero ratio method),这些算法均应用传统的双门限法进行端点检测.同时,为了对比MFPH方法与目前主流方法的优劣性,实验还选取了基于Teager能量算子(TEO,teager energy operator)和经验模态分解(EMD,empirical mode decomposition)(EMD-TEO)的语音端点检测方法进行对比试验.
连续的语音中,语音的起止点无法完全准确地被检测出来,会出现将噪声误检为语音或者将语音漏检,所以不能单纯地考虑某一种检测错误,可按照以下的公式计算语音端点检测的准确率:
| $ p = \left( {1 - \frac{{{N_1} + {N_2}}}{N}} \right) \times 100\% $ | (18) |
其中:N为语音总帧数,N1为语音中语音被漏检的帧数,N2为语音中噪声被误检为语音的帧数,p为准确率.
生成的1200条语音分别使用笔者提出的MFPH、ZCR、SE、EZR和EMD-TEO方法进行端点检测,并计算准确率.
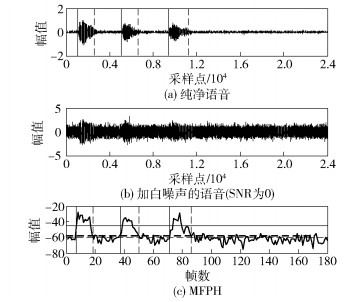
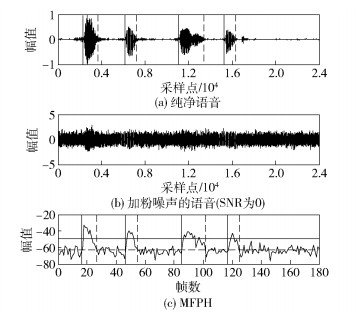
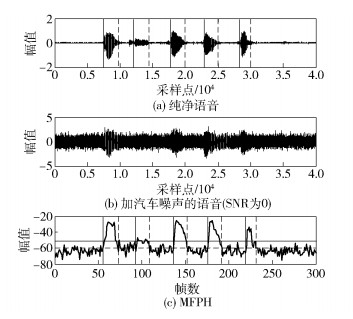
5.2 实验结果分析图 5~7分别为3条语音使用MFPH方法在信噪比为0dB,噪声为白噪声、粉噪声和汽车噪声情况下的端点检测效果.可以看出,MFPH在低信噪比环境下能很好地分辨出语音端和背景噪声段,这是因为SE和梅尔频率倒谱系数都对噪声有比较好的鲁棒性,并且梅尔频率倒谱系数的第1个系数MFCC0比其他部分都大,且有声段大于无声段,能更好地追踪语音.所以将SE和MFCC0的乘积作为新的特征参数能够更加明显地突出语音端和背景噪声段的区别.
|
图 5 信噪比为0的白噪声情况下的端点检测 |
|
图 6 信噪比为0的粉噪声情况下的端点检测 |
|
图 7 信噪比为0的汽车噪声情况下的端点检测 |
根据式(18)计算各方法的端点检测准确率,如表 1所示.
|
|
表 1 端点检测准确率的比较 |
从表 1可知,ZCR方法的检测准确率在信噪比为10dB时相对高,但是在信噪比低于5dB时,准确率急剧下降.因为背景中有反复穿越坐标轴的噪声,制造了大量的虚假过零率,导致低信噪比情况下ZCR检测效果极差. SE方法的检测准确率在噪声为汽车噪声的时候相对较差,因为SE对周期性噪声的鲁棒性较差. EZR方法作为端点检测的特征参数,结合了短时能量和ZCR方法的优点,优势互补,所以检测效果相对ZCR和SE方法较好,但在低信噪比情况下效果依然不理想.因为低信噪比环境中短时能量对语音起始点的判断能力较差,而且又会产生较多的虚假过零率. EMD-TEO方法在3种噪声环境下表现良好,特别是在白噪声情况下效果更好.该方法利用EMD分解,提出筛选IMF分量的条件,使之能处理含噪语音,然后再进行端点检测. MFPH方法能够根据噪声自适应调整端点检测的门限值,且对噪声具有较好的鲁棒性,所以在低信噪比情况下的检测效果要优于其他传统的方法.
6 结束语语音端点检测是语音识别系统中至关重要的处理过程,MFPH算法结合了抗噪声能力较强的SE和MFCC0,取长补短, 并将模糊C均值聚类算法与贝叶斯算法结合进行门限值自适应估计.实验证明,算法在低信噪比环境下的检测效果比常规的SE法有较大的提高,但是依然不尽人意,无法等同短时能量、ZCR等算法在无噪声环境下的效果.
| [1] |
赵力. 语音信号处理[M]. 北京: 机械工业出版社, 2016: 116-117.
|
| [2] |
Cao D, Gao X, Gao L. An improved endpoint detection algorithm based on MFCC cosine value[J]. Wireless Personal Communications, 2017, 95(3): 2073-2090. DOI:10.1007/s11277-017-3958-0 |
| [3] |
Suh Y, Kim H. Multiple acoustic model-based discriminative likelihood ratio weighting for voice activity detection[J]. IEEE Signal Processing Letters, 2012, 19(8): 507-510. DOI:10.1109/LSP.2012.2204978 |
| [4] |
张毅, 倪雷. 基于模糊熵与改进相关向量机的语音端点检测[J]. 华中科技大学学报(自然科学版), 2017, 45(8): 15-19. Zhang Yi, Ni Lei. Speech activity detection based on fuzzy entropy and improved relevance velevance vector machine[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2017, 45(8): 15-19. |
| [5] |
Kim S K. Voice activity detection algorithm using radial basis function network[J]. Electronics Letters, 2004, 40(22): 1454-1455. DOI:10.1049/el:20046064 |
| [6] |
张晓雷, 吴及, 吕萍. 基于支持向量机与多观测复合特征矢量的语音端点检测[J]. 清华大学学报(自然科学版), 2011, 51(9): 1209-1214. Zhang Xiaolei, Wu Ji, Lü Ping. Support vector machine based VAD using the multiple observation compound feature[J]. Journal of Tsinghua University (Science and Technology), 2011, 51(9): 1209-1214. |
| [7] |
胡波, 肖熙. 检测语音端点及基音的概率模型及方法[J]. 清华大学学报(自然科学版), 2013, 53(6): 749-752. Hu Bo, Xiao Xi. Endpoint detection and pitch determination method based on a probability model[J]. Journal of Tsinghua University (Science and Technology), 2013, 53(6): 749-752. |
| [8] |
Davis S B, Mermelstein P. Comparison of parametric representations for monosyllabic word recognition in continuously spoken sentences[J]. Readings in Speech Recognition, 1980, 28(4): 65-74. |
| [9] |
Huang L S, Yang C H. A novel approach to robust speech endpoint detection in car environments[C]//IEEE International Conference on Acoustics, Speech, and Signal Processing, 2000.[S. l.]: IEEE, 2000: 1751-1754.
|
| [10] |
Mcclellan S, Gibson J D. Variable-rate CELP based on subband flatness[J]. Speech and Audio Processing IEEE Transactions on, 1995, 5(2): 120-130. |
| [11] |
Jin L, Cheng J. An improved speech endpoint detection based on spectral subtraction and adaptive sub-band spectral entropy[C]//International Conference on Intelligent Computation Technology and Automation.[S. l.]: IEEE Computer Society, 2010: 591-594.
|
| [12] |
Tian Y, Wu J, Wang Z, et al. Fuzzy clustering and Bayesian information criterion based threshold estimation for robust voice activity detection[C]//IEEE International Conference on Acoustics, Speech, and Signal Processing, 2003.[S. l.]: IEEE, 2003: I-444-I-447.
|
| [13] |
Cobos C, Mendoza M, Manic M, et al. Clustering of web search results based on an iterative fuzzy C-means algorithm and Bayesian information criterion[J]. Information Sciences, 2014, 281(2): 248-264. |
| [14] |
Volinsky C T, Raftery A E. Bayesian information criterion for censored survival models[J]. Biometrics, 2015, 56(1): 256-262. |


