2. 黄河科技学院 信息工程学院, 郑州 450000
为了减少超密集网络中小区间的干扰,提出了一种改进的分簇及资源分配方案.首先,根据小基站间的路径损耗程度构造损耗图,基于损耗图选出簇头并且分簇,将路径损耗之和较小的小基站放在一个簇中,每个簇中小基站的数量不超过子信道的数量;然后,根据簇内的用户在每个子信道上的信干噪比依次为每个簇的用户分配正交的子信道;最后,优化功率分配,以提高吞吐量.仿真结果显示,与相同场景中的已有方案相比,所提方案更加均匀地将小基站分布在每个簇中,并且显著提高了系统吞吐量.
2. School of Information Engineering, Huanghe S & T University, Zhengzhou 450000, China
An improved clustering and resource allocation scheme was proposed for ultra-dense network in order to reduce the interference among small cells. Firstly, a loss graph was constructed according to the path loss among the small base stations, and the cluster head was selected based on the loss graph. Small base stations with the smaller sum of path loss were divided into the one cluster in which the number of small base stations was no more than the number of subchannels. Then, orthogonal subchannels were allocated to users in each cluster according to the signal to interference plus noise ratio on each subchannel of each user in the cluster. Finally, power allocation was optimized to improve throughput. Simulation results show that compared with the existed schemes in the same scenario, the small base stations are more evenly distributed in each cluster, so that the system throughput is improved significantly.
超密集网络(UDN, ultra-dense networks)允许用户自己部署家庭基站或者小基站,缩小用户与基站之间的距离[1],能够增强室内覆盖[2],提高频谱利用率[3],是第5代移动通信系统(5G,the fifth generation of mobile communications system)的关键技术之一[4].但是,在宏基站(MBS, macrocell base station)的覆盖范围内部署大量低功率的小基站(FBS, femtocell base station)也带来了一系列的干扰问题,包括FBS之间的层内干扰以及MBS与FBS之间的层间干扰[5].所以,有效地消减干扰就显得尤其重要.
国内外学者对UDN中的干扰消减方法进行了大量的研究. Kim和Chen等[6-7]将图着色理论应用在分簇中,将干扰较小的FBS归入同一个簇,干扰较大的FBS归入不同的簇中.然而,随着基站的增多,这2种算法对子信道数量的需求也随之增大. Liu等[8]提出了一种两阶段联合分簇和调度算法,利用博弈论将干扰较大的FBS归入同一个簇,干扰较小的FBS归入不同的簇中,但是并没有给出具体的方案. Seno等[9]提出了一种基于矩阵的分簇方法,将干扰信息以二进制数字形式组成一个关联矩阵,通过行列变换进行分簇,然而该方法只能得到少量的簇. Qiu等[10]提出了一种基于干扰图的分簇方法,将FBS分为多个簇和一些独立的节点,这些簇在干扰图上通过独立的节点相连,减少了簇间干扰,但是该方法的实际应用场景受限. Liang等[11]提出了一种基于分簇的节能资源分配算法,首先根据减法聚类选出多个簇头,用K-means算法将FBS分簇,然后在每个簇内以最小化簇内干扰为目标将用户分组,最后使用迭代的方法分配资源块和功率. Wei等[12]提出了一种修正的K-means算法动态地改变簇的数量,并使用一种两阶段子信道分配方案提高用户传输速率. Ahuja等[13]提出了一种分布式干扰图着色方法(DIGC, distributed interference graph coloring),当用户使用的子信道均不相同时开始传输数据. Qiu等[14]提出了分层资源分配框架(HRAF, hierarchical resource allocation framework),将干扰度较大的FBS以及在干扰图中与之相连的FBS都归入一个簇中,该方法可能存在簇内FBS的数量超过子信道数量的情况,无法保证同一簇内的FBS都分配到正交的子信道.
针对Qiu等[14]的不足,笔者提出了UDN中一种改进的分簇和资源分配方案(ICRA, improved clustering and resource allocation).首先,根据FBS间的路径损耗建立损耗图,基于损耗程度和节点的度选出簇头,依次将与簇内FBS的路径损耗之和最小的FBS归入簇内,直到簇内FBS数量达到子信道数量,或者没有归入任何簇的FBS都与该簇内的FBS不相连;然后,根据用户在子信道上的信干噪比(SINR,signal to interference plus noise ratio)依次为每个簇内的用户分配子信道;最后,优化功率分配以提高吞吐量.
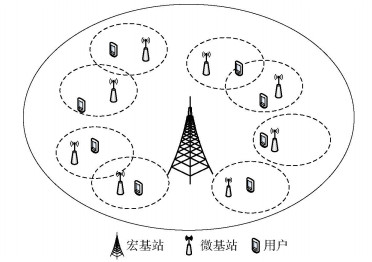
1 系统模型考虑包含1个MBS和J个FBS的UDN,J个FBS随机分布在MBS的覆盖范围内,表示为Sf={f1, f2, …, fJ},如图 1所示.假定在同一时刻每个FBS只服务一个用户. FBS和用户都配置了单根天线. MBS和FBS采用正交的子信道,所以不存在层间干扰. FBS可用的子信道共有M个,用cm表示,m=1, 2, …M.
|
图 1 两层超密集网络模型 |
如果中心控制器同时进行分簇和子信道分配,复杂度极高[14].为此首先考虑分簇,将FBS分为多个簇,然后簇头负责本簇内的子信道分配和功率分配. MBS根据接收到的参考信号测量出FBS间的路径损耗,构造损耗图.基于损耗图将J个FBS分为K个互不重叠的簇并选出簇头,用Qk表示第k个簇,该簇中有Jk个FBS,
用ukf表示Qk内第f个FBS服务的用户,用χk, fm表示子信道cm是否分配给ukf,当χk, fm=1时表示子信道cm分配给了ukf,当χk, fm=0时表示子信道cm没有分配给cm.用Skf, kjm表示ukf在子信道cm上从Qk内的第j个FBS获取的信号的强度,表示为
| $ S_{k f, k j}^{m}=\chi_{k, f}^{m}{g}_{k f, k j}^{m} p_{k f, k j}^{m} $ | (1) |
其中:pkf, kjm为Qk内第j个FBS到ukf的发送功率,gkf, kjm为Qk内第j个FBS与ukf之间的信道增益,表示为
| $ g_{k f, k j}^{m}=d_{k f, k j}^{-\alpha}\left|h_{k f, k j}^{m}\right|^{2} $ | (2) |
其中:dkf, kj为Qk内第j个FBS与ukf之间的距离,α为路径损耗指数,hkf, kjm为Qk内第j个FBS与ukf在子信道cm上的小尺度衰落系数. ukf接收到的信号的信干噪比γkfm可以表达为
| $ \gamma _{kf}^m = \frac{{S_{kf, kf}^m}}{{\sum\limits_{i = 1, i \ne k}^K {\sum\limits_{j = 1}^{{J_i}} {S_{kf, ij}^m} } + {N_0}}} $ | (3) |
其中N0为高斯白噪声的方差.
用Rkfm表示N0在子信道cm上的数据速率,Rkfm可以表示为
| $ R_{k f}^{m}=W {\rm lb} \left(1+\gamma_{k f}^{m}\right) $ | (4) |
其中W为子信道的带宽.系统的吞吐量可以表示为
| $ R=\sum\limits_{k=1}^{K} \sum\limits_{f=1}^{J_{k}} \sum\limits_{m=1}^{M} R_{k f}^{m} $ | (5) |
本文方案的目标是:在一定的约束条件下,合理地分簇并分配资源,以最大化系统吞吐量,如式(6)所示:
| $ {\left\{\chi_{f, k}^{m}, p_{k f, k f}^{m}, k=1, 2, \cdots, K, f=1, 2, \cdots J_{k}\right.}, \\ {m=1, 2, \cdots, M\}=\arg \max \sum\limits_{k=1}^{K} \sum\limits_{f=1}^{J_{k}} \sum\limits_{m=1}^{M} W \operatorname{lb}\left(1+\gamma_{k f}^{m}\right)}\\ \begin{array}{l}{\text { s.t. } \mathrm{C1}: \sum\limits_{m=1}^{M} p_{k f, k f}^{m} \leqslant P_{\mathrm{max}}, \forall k, f} \\~~~~~~~ {\mathrm{C} 2: \sum\limits_{m=1}^{M} \chi_{k, f}^{m}=1, \forall k, f} \\ ~~~~~~~{\mathrm{C} 3: \sum\limits_{f=1}^{J_{k}} \chi_{k, f}^{m} \leqslant 1, \forall k, m}\end{array} $ | (6) |
其中:Pmax为FBS的功率限制条件. C1表示每个FBS的发送功率不超过Pmax,C2表示每个用户只能分配一个子信道,C3表示在同一个簇内每个子信道只能分配给一个用户.
2 分簇方案在Qiu等[14]的分簇结果中,簇内FBS数量会大于子信道数量,无法实现簇内子信道正交,而且基于距离的干扰图过于简单.本文方案基于FBS间的路径损耗建立损耗图,并且保证簇内FBS的数量不超过子信道的数量.具体的分簇方案步骤如下.
步骤1 FBS根据接收到的参考信号测量路径损耗,并设置路径损耗门限T,若2个FBS之间的路径损耗小于T,则认为这2个FBS之间有干扰;否则认为这2个FBS之间没有干扰.
步骤2 FBS之间交换路径损耗信息,构造损耗图,该图中的节点代表FBS,若2个FBS之间的路径损耗小于T,则这2个FBS对应的节点之间有条边,并且边的长度等于路径损耗;否则这2两个FBS对应的节点没有边,并且认为节点之间的距离大于T,T大于损耗图中任何一条边的长度.
步骤3 从步骤2构造出的损耗图中找到一条最短的边,若最短的边有多条,则任意选择一条,比较这条边的2个节点的度,选出度较大的节点做第一个簇的簇头,将这2个节点放入Q1中.
步骤4 从没有被归入任何簇的FBS中选出与Q1中所有FBS的距离之和最小的一个FBS,若满足这一条件的FBS有多个,则随机选取其中一个FBS,将该FBS放入Q1中.
步骤5 重复步骤4,直到Q1中FBS的数量等于M或者剩余的FBS与Q1中所有FBS互不干扰为止.
步骤6 在损耗图中删除Q1中的FBS对应的节点,并且删除与这些节点相连的边,得到新的损耗图.
步骤7 重复上述步骤,直至将所有的度大于零的节点都归到其中的一个簇内,若有度为零的节点,则将每个度为零的节点都放在一个新的簇中.
3 子信道分配方案如果位于不同簇的2个相邻FBS分配到了相同的子信道,则这2个FBS之间的干扰较大,严重影响这2个簇的吞吐量.所以,每个簇的子信道分配不是相互独立的,还需要考虑簇间干扰.
Qiu等[14]首先采用图着色算法为FBS分配子信道,然后考虑协调FBS之间的干扰,该方法只考虑到子信道的正交,并没有考虑用户的信干噪比,吞吐量有待提高.本文方案根据每个用户在每个子信道上的信干噪比依次为每个簇内的用户分配子信道,具体步骤如下.
步骤1 令D1=Q1,用Ψ表示M个子信道组成的集合,其初始值为Ψ={c1, c2, …, cM},按照FBS归入簇的顺序给Qk内的FBS进行编号,分别为sk1, sk2, …, skJk,Jk为Qk内FBS个数,Jk不大于M.
步骤2 计算Q1内每个用户在不同子信道上的信干噪比,用γim表示s1i在子信道cm上的信干噪比,i=1, 2, …, J1,令
步骤3 重复步骤2,直到D1为空集为止.
步骤4 将Q2内的FBS分为两部分:其中一部分FBS与已经分配过子信道的簇之间存在干扰,用s1, s2, …, sy表示,y≤J2;另一部分FBS与已经分配过子信道的簇之间无干扰,簇头首先采用步骤2和步骤3的方法依次为s1, s2, …, sy分配子信道,然后再采用相同的方法为其余的FBS分配子信道.
步骤5 采用上述方法,其余簇的簇头为该簇内FBS分配子信道,直到所有的FBS都分配到子信道.
笔者所提的子信道分配方案中,簇头从可用的子信道中选出信干噪比最大的子信道分配给用户,从而能提高簇内吞吐量.
4 功率分配方案在已知分簇和子信道分配时,功率分配的目标函数为
| $ \begin{aligned}\left\{p_{k f, k f}^{m}, k=1, 2, \cdots, \right.&\left.K, f=1, 2, \cdots J_{k}, m=1, 2, \cdots, M\right\}=\\ & \arg \max \sum\limits_{k=1}^{K} \sum\limits_{f=1}^{J_{k}} \sum\limits_{m=1}^{M} W \operatorname{lb}\left(1+\gamma_{k f}^{m}\right) \\ \text { s. t. } \mathrm{C1}: & \sum\limits_{m=1}^{M} p_{k f, k f}^{m} \leqslant P_{\max }, \forall k, f \\ & \mathrm{C} 2: p_{k f, k f}^{m} \geqslant 0, \forall k, f \end{aligned} $ | (7) |
目标函数是功率的连续可分函数,因此每个局部最优解都满足KKT定理:对于式(7),存在局部最优解
| $ \begin{array}{c} \frac{{\partial \left( {\sum\limits_{m = 1}^M {\chi _{k, f}^m} {\rm{lb}}\left( {1 + \frac{{g_{kf, kf}^mp_{kf, kf}^m}}{{\sum\limits_{i = 1, i \ne k}^K {\sum\limits_{j = 1}^L {g_{kf, ij}^m} } p_{kf, ij}^m + {N_0}}}} \right)} \right)}}{{\partial p_{kf, kf}^m}} + \\ \frac{{\partial \left( {\sum\limits_{k = 1}^K {\sum\limits_{f = 1}^{{J_k}} {\sum\limits_{m = 1}^M {\chi _{k, f}^m} } } {\mathop{\rm lb}\nolimits} \left( {1 + \frac{{g_{kf, kf}^mp_{kf, kf}^m}}{{\sum\limits_{i = 1}^K {\sum\limits_{j = 1}^K {g_{kf, ij}^m} } p_{kf, ij}^m + {N_0}}}} \right)} \right)}}{{\partial p_{kf, kf}^m}} - \\ \lambda _k^{k{f^*}} + \mu _{k, m}^{k{f^*}} = 0 \end{array} $ | (8) |
| $ \lambda _k^{k{f^*}}\left( {\sum\limits_{m = 1}^M {\chi _{k, j}^m} p_{kf, kf}^m - {P_{\max }}} \right) = 0 $ | (9) |
| $ \mu_{k, m}^{k f^{*}} p_{k f, k f}^{m}=0 $ | (10) |
根据式(8),功率分配的目标函数简化为
| $ \begin{array}{c} \frac{{\partial \left( {\sum\limits_{m = 1}^M {\chi _{k, f}^m} {\rm{lb}}\left( {1 + \frac{{g_{kf, kf}^m, p_{kf, kf}^m}}{{\sum\limits_{i = 1, i \ne k}^K {\sum\limits_{j = 1}^{{J_i}} {g_{kf, ij}^m} } p_{kf, ij}^m + {N_0}}}} \right)} \right)}}{{\partial p_{kf, kf}^m}} - \\ \left( {\sum\limits_{i = 1, i \ne k}^K {\sum\limits_{j = 1}^{{J_i}} {\chi _{k, f}^m} } g_{kf, ij}^m + {z_{kf}}} \right) - \lambda _k^{k{f^*}} = 0\\ {\rm{ s}}{\rm{. t}}{\rm{. C1}}:\sum\limits_{m = 1}^M {\chi _{k, f}^m} p_{kf, kf}^m \le {P_{\max }}, \forall k, f \end{array} $ | (11) |
其中zkf为加性高斯白噪声.
利用注水算法可求得每个子信道m上的功率分配的最优解为
| $ \begin{array}{c} p_{kf, kf}^m = \frac{1}{{\ln 2\left( {{\lambda _f} + \sum\limits_{i = 1, i \ne k}^K {\sum\limits_{j = 1}^{{J_i}} {\chi _{k, f}^m} } g_{kf, ij}^m + {z_{kf}}} \right)}} - \\ \frac{{\sum\limits_{i = 1, i \ne k}^K {\sum\limits_{j = 1}^{{J_i}} {\chi _{k, f}^m} } g_{kf, ij}^mp_{kf, ij}^m + {N_0}}}{{g_{kf, kf}^m}} \end{array} $ | (12) |
在分簇过程中,每个FBS测量自身与其余J-1个FBS之间的路径损耗,构造损耗图并且分簇,该过程与Qiu等[14]的分簇方案类似,两种方案的计算复杂度均为
仿真了本文方案的性能,并与已有方案做比较.仿真环境如下:在200 m×200 m的区域内部署了一个MBS和多个FBS.具体仿真参数如表 1所示,参与对比的算法有Ahuja等[13]所提的DIGC算法、Qiu等[14]提出的HRAF方案.
|
|
表 1 仿真参数 |
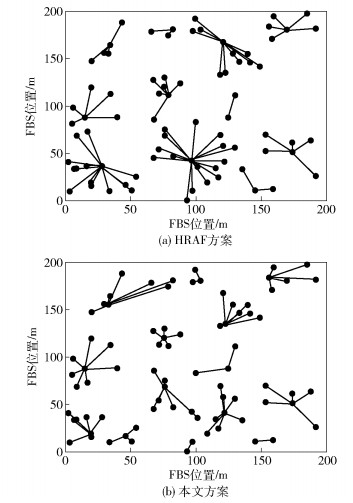
图 2所示为本文方案和HRAF方案的分簇,80个FBS在场景中的随机分布. Qiu等[14]将80个FBS分为11个簇,最大的簇包含17个FBS,最小的簇包含2个FBS;本文方案将80个FBS分为14个簇,最大的簇包含8个FBS,最小的簇包含2个FBS.本文方案更加均匀地将FBS分布在每个簇中,不但能降低簇头的计算复杂度,还能减少对子信道数量的需求,提高子信道利用率.
|
图 2 2种方案的分簇 |
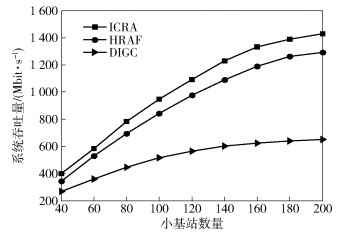
图 3仿真了3种方案在不同FBS数量下的系统吞吐量,仿真环境中的子信道数量为8.从图 3可以看出,随着FBS数量的增加,本文方案的系统吞吐量明显高于其他两种方案.这是因为本文方案在分配子信道时,考虑到了每个FBS在每个子信道上的信干噪比.
|
图 3 不同FBS数量下的系统吞吐量 |
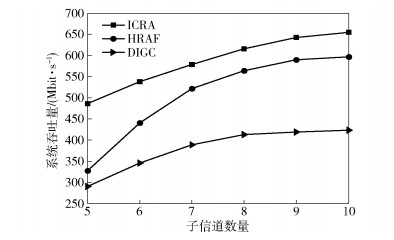
图 4仿真了3种方案在不同子信道数量下的系统吞吐量,仿真环境中FBS的数量为80.从图 4可以看出,随着子信道数量的增加,3种方案的系统吞吐量都得到了提高.这是因为可用的子信道越多,就越能避开干扰,从而能传输更多的有用信号.从图中还可以看出,本文方案的系统吞吐量显著高于其他两种方案,这是以增加分配子信道的复杂度为代价换取的吞吐量的提升.
|
图 4 不同子信道数量下的系统吞吐量 |
所提的UDN中的分簇及子信道分配方案,根据FBS间的路径损耗进行分簇并选出簇头,根据FBS在不同子信道上的信干噪比为用户分配子信道,考虑到了簇间干扰,最后优化功率分配,以增大吞吐量.与相同场景中的已有方案相比,本文方案更加均匀地将FBS分布在每个簇中,显著提升了系统吞吐量,其分簇的复杂度与已有方案相同,分配子信道的复杂度略高于已有方案.然而,本文方案假定每个FBS只服务一个用户,如果将该方案扩展到每个FBS服务多个用户的场景还有待于研究.
| [1] |
Hwang I, Song B, Soliman S S. A holistic view on hyper-dense heterogeneous and small cell networks[J]. IEEE Communications Magazine, 2013, 51(6): 20-27. DOI:10.1109/MCOM.2013.6525591 |
| [2] |
Liu Junyu, Sheng Min, Liu Lei, et al. Interference management in ultra-dense networks:challenges and approaches[J]. IEEE Network, 2017, 31(6): 70-77. DOI:10.1109/MNET.2017.1700052 |
| [3] |
Yang Chungang, Li Jiandong, Ni Qiang, et al. Interference-aware energy efficiency maximization in 5G ultra-dense networks[J]. IEEE Transactions on Communications, 2017, 65(2): 728-739. DOI:10.1109/TCOMM.2016.2638906 |
| [4] |
Kamel M, Hamouda W, Youssef A. Ultra-dense detworks:a survey[J]. IEEE Communications Surveys and Tutorials, 2016, 18(4): 2522-2545. DOI:10.1109/COMST.2016.2571730 |
| [5] |
Zhou Li, Hu Xiping, Ngai E C H, et al. A dynamic graph-based scheduling and interference coordination approach in heterogeneous cellular networks[J]. IEEE Transactions on Vehicular Technology, 2016, 65(5): 3735-3748. DOI:10.1109/TVT.2015.2435746 |
| [6] |
Kim S J, Cho I K, Lee B B, et al. Multi-cluster based dynamic channel assignment for dense femtocell networks[J]. KSII Transactions on Internet and Information Systems, 2016, 10(4): 1535. |
| [7] |
Chen Lu, Xia Hailun, Feng Chunyan, et al. Clustering-based co-tier interference coordination in dense small cell networks[C]//IEEE 26th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications. New York: IEEE Press, 2015: 1878-1882.
|
| [8] |
Liu Ling, Garcia V, Tian Lin, et al. Joint clustering and inter-cell resource allocation for CoMP in ultra dense cellular networks[C]//IEEE International Conference on Communications. New York: IEEE Press, 2015: 2560-2564. https://ieeexplore.ieee.org/document/7248710
|
| [9] |
Seno R, Ohtsuki T, Jiang Wenjie, et al. A low-complexity cell clustering algorithm in dense small cell networks[J]. EURASIP Journal on Wireless Communications and Networking, 2016, 2016(1): 262. |
| [10] |
Qiu Junfei, Wu Qihui, Xu Yuhua, et al. Demand-aware resource allocation for ultra-dense small cell networks:an interference-separation clustering-based solution[J]. Transactions on Emerging Telecommunications Technologies, 2016, 27(8): 1071-1086. DOI:10.1002/ett.3046 |
| [11] |
Liang Liang, Wang Wen, Jia Yunjia, et al. A cluster-based energy-efficient resource management scheme for ultra-dense networks[J]. IEEE Access, 2016, 4(99): 6823-6832. |
| [12] |
Wei Rong, Wang Ying, Zhang Yuan. A two-stage cluster-based resource management scheme in ultra-dense networks[C]//IEEE/CIC International Conference on Communications in China. New York: IEEE Press, 2015: 738-742. https://ieeexplore.ieee.org/document/7008373
|
| [13] |
Ahuja K, Xiao Yuanzhang, van der Schaar M. Distributed interference management policies for heterogeneous small cell networks[J]. IEEE Journal on Selected Areas in Communications, 2015, 33(6): 1112-1126. DOI:10.1109/JSAC.2015.2417014 |
| [14] |
Qiu Junfei, Ding Guoru, Wu Qihui, et al. Hierarchical resource allocation framework for hyper-dense small cell networks[J]. IEEE Access, 2016, 4(99): 8657-8669. |



