2. 成都信息工程大学 控制工程学院, 成都 610225
针对一类具有外干扰和建模误差的n阶非线性系统提出一种有限时间Back-stepping动态面控制.在动态面控制方法的子系统控制器设计中设计一个快速有限时间收敛的非线性滤波器,以代替一阶线性滤波器.该方法可避免"计算膨胀",降低高阶系统的误差积累,同时可避免高阶系统有限时间控制难以解决的奇异性问题.针对动态面控制稳定性分析中未将估计误差考虑在内的不足,将其一并考虑,并证明了其稳定性,给出稳态控制误差.最后结合四旋翼飞行器位置控制系统仿真验证了其工程的实用性和优越性.
2. Chengdu University of Information Technology School of Control Engineering, Chengdu 610225, China
A finite time back-stepping dynamic surface control was proposed for n-order nonlinear systems with external disturbances and modeling errors. In the subsystem controller design of the dynamic surface control method, a nonlinear filter with fast finite time convergence was designed to replace the first order linear filter. This method can avoid "explosion of terms", reduce the error accumulation of high order system, and at the same time can avoid the singularity problem that is difficult to solve in high order system of finite time control. In order to solve the problem that the estimation error was not taken into account in the stability analysis of dynamic surface control, the stability of the estimation error was considered, and the steady-state control error was given. Finally, combining with the position control of the four-rotor aircraft, the simulation verifies its engineering practicability and superiority.
近几十年来, 线性系统控制取得大量成果,如精确线性化[1]、滑模控制[2]和Back-stepping控制[3]等.与其他控制方法相比, Back-stepping控制在高阶不确定系统的控制器设计问题上具有明显优势, 因此被广泛用于飞行器控制[4]、水下航行器控制[5]、直流电机控制[6]等方面.但在Back-stepping控制器设计中, 需对虚拟控制律求导, 因此出现了“计算膨胀”[3]的问题.
为了克服“计算膨胀”,Swaroop[7]提出动态面控制技术. Xu等[8-13]将动态面技术与现有其他技术结合, 改进了动态面部分性能,但仍未有根本性改进. Wang[14]提出指数项为(0, 1)之间形式的非线性滤波器, 使滤波器在跟踪误差较小时收敛速度加快,滤波器的滤波效果有一定提高.但当跟踪误差较大时, 该滤波器的效果变差, 且未考虑滤波器对虚拟控制量一阶微分的估计误差.虽然动态面技术已得到广泛应用和发展, 但少有学者提及动态面是通过滤波器得到虚拟控制律一阶微分的估计值, 从而避免“计算膨胀”.因此得到虚拟控制律一阶微分才是引入滤波器的根本目的.所以滤波器对输入信号一阶微分的估计性能决定着动态面方法的性能.
笔者以一类具有外干扰和建模误差的n阶非线性系统为对象, 提出有限时间Back-stepping动态面控制, 以动态面为基础, 参考快速终端滑模控制[15], 引入快速有限时间收敛的非线性滤波器, 降低高阶系统控制中的误差积累, 改善了系统性能, 并考虑了包括跟踪误差、滤波器滤波误差和滤波器对虚拟控制律一阶微分估计误差在内的各种误差, 利用Lyapunov方法严格证明了n阶系统闭环的稳定性, 解出稳态误差.最后结合工程中阶数较高的飞行器位置系统做控制对象进行了仿真验证.本文方法是在动态面基础上的改进, 继承了动态面应用的广泛性, 适合于工程应用.
1 问题描述考虑具有外干扰和建模误差的n阶非线性系统:
| $ \begin{array}{l} {{\dot x}_1} = {x_2} + {f_1}\left( {{x_1}} \right) + {d_1}\left( {{x_1},t} \right)\\ {{\dot x}_2} = {x_3} + {f_2}\left( {{x_1},{x_2}} \right) + {d_2}\left( {{x_1},{x_2},t} \right)\\ \; \vdots \\ {{\dot x}_i} = {x_{i + 1}} + {f_i}\left( {{x_1}, \cdots ,{x_i}} \right) + {d_i}\left( {{x_1}, \cdots ,{x_i},t} \right)\\ \; \vdots \\ {{\dot x}_{n - 1}} = {x_n} + {f_{n - 1}}\left( {{x_1}, \cdots ,{x_{n - 1}}} \right) + {d_{n - 1}}\left( {{x_1}, \cdots ,{x_{n - 1}},t} \right)\\ {{\dot x}_n} = u.\\ y = {x_1} \end{array} $ |
其中:fi(x1, …, xi)(1≤i≤n)为已知非线性项,且充分光滑;di(x1, …, xi, t)(1≤i≤n)为外干扰及建模误差之和,其值未知,但其受限于已知充分光滑非线性函数ρi(x1, …, xi, t),满足|di(x1, …, xi, t)|≤|ρi(x1, …, xi, t)|;u为系统控制,y为系统输出.
控制目标为设计控制器u,使系统输出y,跟踪给定参考轨迹yr,且保证闭环所有信号一致,最终有界.
1.1 常规动态面存在的问题动态面[8]中一阶线性滤波器对输入的信号跟踪速度慢, 导致动态过程中滤波误差大, 在高阶系统中造成误差积累.针对上述问题, 提出快速有限时间收敛的滤波器, 同时对2种滤波器进行分析.
为完成控制目标, 做出以下假设.
假设1 参考轨迹xd连续有界, 且存在三阶有界导数, 即
引理1 杨不等式方程[8]为
| $ \frac{{{a^2} + {b^2}}}{{2\varepsilon }} + \frac{\varepsilon }{2} \ge ab $ | (1) |
其中:a、b大于0;ε为任意正实数, 当且仅当a=b时等号成立.
1.2 一阶线性滤波器分析对于动态面中的一阶线性滤波器:
| $ \begin{array}{*{20}{c}} {{{\dot x}_d} + \tau \left( {{x_d} - {x_e}} \right) = 0}\\ {{x_d}(0) = {x_e}(0)} \end{array} $ | (2) |
其中:xd为输出信号, xe为输入信号, τ为正常数.
令滤波误差e=xd-xe, 其动力学方程为
| $ \dot e = - \tau e - {{\dot x}_e} $ | (3) |
可得滤波误差的收敛速度为
对式(2)等号两边求导得
| $ \ddot e = - \tau \dot e - {{\ddot x}_e} $ | (4) |
令
| $ \dot \xi = - \tau \xi - {{\ddot x}_e} $ | (5) |
由式(5)可知滤波器对期望值一阶微分估计误差的收敛速度为
定理1 对于滤波器
| $ \begin{array}{*{20}{c}} {{{\dot x}_d} + \alpha \left( {{x_d} - {x_e}} \right) + \beta {{\left( {{x_d} - {x_e}} \right)}^{q/p}} = 0}\\ {{x_d}(0) = {x_e}(0)} \end{array} $ | (6) |
其中:xd为输出信号, xe为输入信号.若α、β均为正常数, p、q为正奇数, 且满足p>q, 则对于任意的输入信号xe∈L[0, ∞),滤波器的输出xd可以在有限时间内跟踪上输入信号, 即滤波误差可以在有限时间内收敛.
证明
由假设1可知, 输入信号xe为有界值, 因此可取其最大值xe,max,求时间上限.
式(6)可写为
| $ \frac{{{\rm{d}}\left( {{x_d} - {x_{e,\max }}} \right)}}{{{\rm{d}}t}} + \alpha \left( {{x_d} - {x_{e,\max }}} \right) + \beta {\left( {{x_d} - {x_{e,\max }}} \right)^{q/p}} = 0 $ | (7) |
由式(7)得
| $ \begin{array}{*{20}{c}} {{{\left( {{x_d} - {x_{e,\max }}} \right)}^{ - q/p}}\frac{{{\rm{d}}\left( {{x_d} - {x_{e,\max }}} \right)}}{{{\rm{d}}t}} + }\\ {\alpha {{\left( {{x_d} - {x_{e,\max }}} \right)}^{1 - q/p}} = - \beta } \end{array} $ | (8) |
令y=(xd-xe,max)1-q/p, 则式(8)可以写为
| $ \frac{{{\rm{d}}y}}{{{\rm{d}}t}} - \frac{{p - q}}{p}\alpha y = - \frac{{p - q}}{p}\beta $ | (9) |
解式(9)得跟踪误差的收敛上界为
| $ t = \frac{p}{{\alpha (p - q)}}\ln \frac{{\alpha {{\left( {{x_d}(0) - {x_{e,\max }}} \right)}^{(p - q)/p}} + \beta }}{\beta } $ | (10) |
由上式知跟踪误差可实现有限时间内收敛.
对于非线性滤波器, 考虑其跟踪误差e=xd-xe, 则动力学方程可以写为
| $ \dot e = - \alpha e - \beta {e^{q/p}} - {{\dot x}_e} $ | (11) |
由式(11)可知,非线性滤波器滤波误差的收敛速度为
对式(11)等号两边同时求导得
| $ \ddot e = - \alpha \dot e - \beta \frac{q}{p}{e^{(q - p)/p}}\dot e - {{\ddot x}_e} $ | (12) |
令
| $ \dot \xi = - \alpha \xi - \beta \frac{q}{p}{e^{(q - p)/p}}\xi - {{\ddot x}_e} $ | (13) |
非线性滤波器对输入信号一阶微分估计产生的估计误差收敛速度为
定理1得证.
2 控制器设计控制器设计步骤如下.
第1步 定义系统跟踪误差z1为
| $ {z_1} = {x_1} - {x_{1d}} $ | (14) |
对其求导得
| $ \begin{array}{*{20}{c}} {{{\dot z}_1} = {{\dot x}_1} - {{\dot x}_{1d}} = }\\ {{x_2} + {f_1}\left( {{x_1}} \right) + {d_1}\left( {{x_1},t} \right) - {{\dot x}_{1d}}} \end{array} $ | (15) |
设计虚拟控制律x2e为
| $ {x_{2e}} = - {K_1}{z_1} - {f_1}\left( {{x_1}} \right) - \frac{{{z_1}\rho _1^2}}{{2\varepsilon }} + {{\dot x}_{1d}} $ | (16) |
其中:K1为正实数,ε为任意小正实数.
采用式(6)形式的非线性滤波器, 则滤波器的跟踪误差e2可以定义为
| $ {e_2} = {x_{2d}} - {x_{2e}} $ | (17) |
第2步 定义第2阶子系统的跟踪误差z2为
| $ {z_2} = {x_2} - {x_{2d}} $ | (18) |
在式(17)、式(18)的基础上, 结合了1级子系统的虚拟控制律(式(16)), 则式(15)可以表示为
| $ \begin{array}{*{20}{c}} {{{\dot z}_1} = {x_2} - {x_{2d}} + {x_{2d}} - {x_{2e}} + {x_{2e}} + {f_1}\left( {{x_1}} \right) + }\\ {{d_1}\left( {{x_1},t} \right) - {{\dot x}_{1d}} = }\\ {{z_2} + {e_2} - {K_1}{z_1} + {f_1}\left( {{x_1}} \right) - {f_1}\left( {{x_1}} \right) + }\\ {{d_1}\left( {{x_1},t} \right) - \frac{{{z_1}\rho _1^2}}{{2\varepsilon }} + {{\dot x}_{1d}} - {{\dot x}_{1d}} = }\\ { - {K_1}{z_1} + {z_2} + {e_2} + {d_1}\left( {{x_1},t} \right) - \frac{{{z_1}\rho _1^2}}{{2\varepsilon }}} \end{array} $ | (19) |
滤波器对控制律一阶微分的估计误差ξ2为
| $ {\xi _2} = {{\dot x}_{2d}} - {{\dot x}_{2e}} $ | (20) |
第i步 对于第i(2≤i≤n-1)阶则可以定义
| $ {z_i} = {x_i} - {x_{id}} $ | (21) |
对其求导可得
| $ \begin{array}{*{20}{c}} {{{\dot z}_i} = {{\dot x}_i} - {{\dot x}_{id}} = }\\ {{x_{i + 1}} + {f_i}\left( {{x_1}, \cdots ,{x_i}} \right) + {d_i}\left( {{x_1}, \cdots ,{x_i},t} \right) - {{\dot x}_{id}}} \end{array} $ | (22) |
同时设虚拟控制量为
| $ {x_{i + 1,e}} = - {K_i}{z_i} - {f_i}\left( {{x_1}, \cdots ,{x_i}} \right) - \frac{{{z_i}\rho _i^2}}{{2\varepsilon }} + {{\dot x}_{id}} $ | (23) |
让xi+1, e通过第i个滤波器, 则式(22)可以改写为
| $ {{\dot z}_i} = - {K_i}{z_i} + {z_{i + 1}} + {e_{i + 1}} + {d_i}\left( {{x_1}, \cdots ,{x_i},t} \right) - \frac{{{z_i}\rho _i^2}}{{2\varepsilon }} $ | (24) |
滤波器的跟踪误差ei+1为
| $ {e_{i + 1}} = {x_{i + 1,d}} - {x_{i + 1,e}} $ | (25) |
滤波器对控制量一阶微分的估计误差ξi+1为
| $ {\xi _{i + 1}} = {{\dot x}_{i + 1,d}} - {{\dot x}_{i + 1,e}} $ | (26) |
第n步 对于第n阶定义误差量
| $ {z_n} = {x_n} - {x_{nd}} $ | (27) |
| $ {{\dot z}_n} = {{\dot x}_n} - {{\dot x}_{nd}} $ | (28) |
所以控制器u可以设计为
| $ u = {{\dot x}_{nd}} - {K_n}{z_n} $ | (29) |
定理2 针对以上n阶非线性系统可在由基于快速有限时间收敛的非线性滤波器(见式(6))设计的控制器(见式(29))作用下, 系统输出y可以快速准确地跟踪上系统期望信号yr, 且保证误差收敛到任意小半径的闭球内.
证明
针对z1定义候选李雅普诺夫函数Vz1
| $ {V_{z1}} = \frac{1}{2}z_1^2 $ | (30) |
对其求导可得
| $ {{\dot V}_{z1}} = {{\dot z}_1}{z_1} $ | (31) |
将式(19)代入式(31)可得
| $ \begin{array}{*{20}{c}} {{{\dot V}_{z1}} = {z_1}\left( { - {K_1}{z_1} + {z_2} + {e_2} + {d_1}\left( {{x_1},t} \right) - \frac{{{z_1}\rho _1^2}}{{2\varepsilon }}} \right) = }\\ { - {K_1}z_1^2 + {z_1}{z_2} + {z_1}{e_2} + {z_1}{d_1} - \frac{{z_1^2\rho _1^2}}{{2\varepsilon }}} \end{array} $ | (32) |
由引理1可得
| $ \frac{{z_1^2\rho _1^2}}{{2\varepsilon }} + \frac{\varepsilon }{2} \ge {z_1}{\rho _1}\left( {{x_1},t} \right) \ge {z_1}{d_1}\left( {{x_1},t} \right) $ |
| $ \frac{{z_1^2}}{2} + \frac{{z_2^2}}{2} \ge {z_1}{z_2} $ |
| $ \frac{{z_1^2}}{2} + \frac{{e_2^2}}{2} \ge {z_1}{e_2} $ |
因此式(32)可以写为
| $ \begin{array}{*{20}{c}} {{{\dot V}_{z1}} \le - {K_1}z_1^2 + {z_1}{z_2} + {z_1}{e_2} + \frac{\varepsilon }{2} \le }\\ { - {K_1}z_1^2 + \frac{{2z_1^2 + z_2^2 + e_2^2}}{2} + \frac{\varepsilon }{2}} \end{array} $ | (33) |
对于第1阶子系统中使用的非线性滤波器跟踪误差, 可以构造候选李雅普诺夫函数Ve1, 有
| $ {V_{{e_1}}} = \frac{1}{2}e_2^2 $ | (34) |
根据第1阶子系统中滤波器对虚拟控制量一阶微分的估计误差, 可构造出候选李雅普诺夫函数Vξ1,
| $ {V_{{\xi _1}}} = \frac{1}{2}\xi _2^2 $ | (35) |
对其分别求导可得
| $ {{\dot V}_{{e_1}}} = {e_2}{{\dot e}_2} $ | (36) |
| $ {{\dot V}_{{\xi _1}}} = {\xi _2}{{\dot \xi }_2} $ | (37) |
对滤波器的跟踪误差求导得
| $ \begin{array}{*{20}{c}} {{{\dot e}_2} = {{\dot x}_{2d}} - {{\dot x}_{2e}} = }\\ { - {\alpha _2}\left( {{x_{2d}} - {x_{2e}}} \right) - {\beta _2}{{\left( {{x_{2d}} - {x_{2e}}} \right)}^{q/p}} - {{\dot x}_{2e}} = }\\ { - {\alpha _2}{e_2} - {\beta _2}e_2^{q/p} + {\eta _2}\left( {{z_1},{x_1},{x_{1d}},{{\dot x}_{1d}},{{\ddot x}_{1d}}} \right)} \end{array} $ | (38) |
其中
| $ \begin{array}{*{20}{c}} {{\eta _2}\left( {{z_1},{x_1},{x_{1d}},{{\dot x}_{1d}},{{\ddot x}_{1d}}} \right) = - {k_1}\left( {{{\dot x}_1} - {{\dot x}_{1d}}} \right) - \frac{{{\rm{d}}{f_1}}}{{{\rm{d}}{x_1}}} - }\\ {\frac{{\left( {{{\dot x}_1} - {{\dot x}_{1d}}} \right)\rho _1^2}}{{2\varepsilon }} - \frac{{{z_1}{\rho _1}{\rm{d}}{\rho _1}}}{\varepsilon } + {{\ddot x}_{1d}}} \end{array} $ |
| $ \frac{{{\rm{d}}{\rho _1}}}{{{\rm{d}}t}} = \frac{{\partial {\rho _1}}}{{\partial {x_1}}}{{\dot x}_1},\left| {\frac{{{\rm{d}}{\rho _1}}}{{{\rm{d}}t}}} \right| \le {\mathit{\Phi }_1}\left( {{z_1},{x_1},{x_{1d}},{K_1},{\alpha _1},{{\dot x}_{1d}}} \right) $ |
因此由假设1可知, η2为连续有界函数.
对估计误差求导得
| $ \begin{array}{*{20}{c}} {{{\dot \xi }_2} = {{\ddot x}_{2d}} - {{\ddot x}_{2e}} = }\\ {\frac{{\rm{d}}}{{{\rm{d}}x}}\left( { - {\alpha _2}\left( {{x_{2d}} - {x_{2e}}} \right) - {\beta _2}{{\left( {{x_{2d}} - {x_{2e}}} \right)}^{q/p}}} \right) - {{\ddot x}_{2e}} = }\\ {\frac{{\rm{d}}}{{{\rm{d}}x}}\left( { - {\alpha _2}{e_2} - {\beta _2}e_2^{q/p}} \right) - {{\ddot x}_{2e}} = }\\ { - {\alpha _2}{\xi _2} - {\beta _2}\frac{q}{p}e_2^{(q - p)/p}{\xi _2} + {\zeta _2}} \end{array} $ | (39) |
其中
| $ \begin{array}{*{20}{c}} {{\zeta _2} = - {k_1}\left( {{{\ddot x}_1} - {{\ddot x}_{1d}}} \right) - {{\ddot f}_1}\left( {{x_1}} \right) - \frac{{\left( {{{\ddot x}_1} - {{\ddot x}_{1d}}} \right)\rho _1^2}}{{2\varepsilon }} - }\\ {\frac{{\left( {{{\dot x}_1} - {{\dot x}_{1d}}} \right)}}{\varepsilon }{\rho _1}\frac{{{\rm{d}}{\rho _1}}}{{{\rm{d}}t}} - \frac{{2\left( {{{\dot x}_1} - {{\dot x}_{1d}}} \right){\rho _1}}}{\varepsilon }\frac{{{\rm{d}}{\rho _1}}}{{{\rm{d}}t}} - }\\ {\frac{{{z_1}}}{\varepsilon }{{\left[ {\frac{{{\rm{d}}{\rho _1}}}{{{\rm{d}}t}}} \right]}^2} - \frac{{{z_1}{\rho _1}}}{\varepsilon }{{\ddot \rho }_1} + {{\dddot x}_{1d}}} \end{array} $ |
同理, 由假设1可知ζ2也为连续有界函数.
因此将式(38)和式(39)分别代入式(36)和式(37), 有
| $ {{\dot V}_{{e_1}}} = - {\alpha _2}e_2^2 - {\beta _2}e_2^{(q + p)/p} + {\eta _2}{e_2} $ | (40) |
| $ {{\dot V}_{{\xi _1}}} = - {\alpha _2}\xi _2^2 - {\beta _2}\frac{q}{p}e_2^{(q - p)/p}\xi _2^2 + {\zeta _2}{\xi _2} $ | (41) |
同理对第i阶子系统均可以构造出候选李雅普诺夫函数Vei、Vξi、Vzi.
| $ {{\dot V}_{{e_i}}} = - {\alpha _{i + 1}}e_{i + 1}^2 - {\beta _{i + 1}}e_{i + 1}^{(q + p)/p} + {\eta _{i + 1}}{e_{i + 1}} $ | (42) |
| $ {{\dot V}_{{\xi _i}}} = - \alpha \xi _{i + 1}^2 - \beta \frac{q}{p}e_{i + 1}^{(q - p)/p}\xi _{i + 1}^2 + {\zeta _{i + 1}}{\xi _{i + 1}} $ | (43) |
| $ {{\dot V}_{zi}} \le - {K_i}z_i^2 + \frac{{2z_i^2 + z_{i + 1}^2 + e_{i + 1}^2}}{2} + \frac{\varepsilon }{2} $ | (44) |
Swaroop[7]在稳定性分析时只考虑了系统的跟踪误差和滤波器的滤波误差, 因此只令V=Vz1+,…,+Vzn+Ve1+,…,+Ven-1,但将滤波器对输入信号一阶微分的估计误差考虑进系统的稳定性中是十分必要的, 所以在考虑系统中存在的误差以后, 令V=Vz1+,…,+Vzn+Ve1+,…,+Ven-1+Vξ1+,…,+Vξn-1,则
| $ \begin{array}{*{20}{c}} {\dot V \le - \sum\limits_{i = 1}^n {{K_i}} z_i^2 - \sum\limits_{i = 1}^{n - 1} {{\alpha _{i + 1}}} e_{i + 1}^2 - \sum\limits_{i = 1}^{n - 1} {{\alpha _{i + 1}}} \xi _{i + 1}^2 - }\\ {\sum\limits_{i = 1}^{n - 1} {{\beta _{i + 1}}} e_{i + 1}^{(p + q)/p} - \sum\limits_{i = 1}^{n - 1} {{\beta _{i + 1}}} \frac{q}{p}e_{i + 1}^{(p - q)/p}\xi _{i + 1}^2 + }\\ {\sum\limits_{i = 1}^{n - 1} {\left[ {\frac{{2z_i^2 + z_{i + 1}^2 + e_{i + 1}^2}}{2} + {\eta _{i + 1}}{e_{i + 1}} + {\zeta _{i + 1}}{\xi _{i + 1}}} \right]} + \frac{{n\varepsilon }}{2}} \end{array} $ | (45) |
由上述可知,ηi+1具有一个最大值Mi+1,ζi+1具有一个最大值Ni+1, 同时结合引理1,式(45)可改写为
| $ \begin{array}{*{20}{c}} {\dot V \le - \sum\limits_{i = 1}^n {{K_i}} z_i^2 - \sum\limits_{i = 1}^{n - 1} {\left[ {{\alpha _{i + 1}}e_{i + 1}^2 + {\alpha _{i + 1}}\xi _{i + 1}^2} \right]} - }\\ {\sum\limits_{i = 1}^{n - 1} {\left[ {{\beta _{i + 1}}e_{i + 1}^{(p + q)/p} + {\beta _{i + 1}}\frac{q}{p}e_{i + 1}^{(p - q)/p}\xi _{i + 1}^2} \right]} + }\\ {\sum\limits_{i = 1}^{n - 1} {\left[ {\frac{{2z_i^2 + z_{i + 1}^2 + e_{i + 1}^2}}{2} + \frac{{M_{i + 1}^2e_{i + 1}^2}}{{2\varepsilon }}\frac{{\eta _{i + 1}^2}}{{M_{i + 1}^2}}} \right]} + }\\ {\sum\limits_{i = 1}^{n - 1} {\left[ {\frac{{N_{i + 1}^2{\bf{ \pmb{\mathsf{ ξ}} }}_{i + 1}^2\zeta _{i + 1}^2}}{{2\varepsilon }}\frac{{\zeta _{i + 1}^2}}{{N_{i + 1}^2}} + \varepsilon } \right]} + \frac{{n\varepsilon }}{2}} \end{array} $ | (46) |
取
| $ \begin{array}{*{20}{c}} {\dot V \le - \sum\limits_{i = 1}^n {az_i^2} - \sum\limits_{i = 1}^{n - 1} {\left[ {a\left( {e_{i + 1}^2 + \xi _{i + 1}^2} \right) - } \right.} }\\ {\left. {\left( {1 - \frac{{\eta _{i + 1}^2}}{{M_{i + 1}^2}}} \right)\frac{{M_{i + 1}^2e_{i + 1}^2}}{{2\varepsilon }}} \right] - }\\ {\sum\limits_{i = 1}^{n - 1} {\left[ {\left( {1 - \frac{{\zeta _{i + 1}^2}}{{N_{i + 1}^2}}} \right)\frac{{N_{i + 1}^2\xi _{i + 1}^2}}{{2\varepsilon }}} \right]} + \frac{{(3n - 1)\varepsilon }}{2} \le }\\ { - \sum\limits_{i = 1}^n {az_i^2} - \sum\limits_{i = 1}^{n - 1} a \left( {e_{i + 1}^2 + \xi _{i + 1}^2} \right) + \frac{{(3n - 1)\varepsilon }}{2} \le }\\ { - 2aV + \frac{{(3n - 1)\varepsilon }}{2}} \end{array} $ | (47) |
由式(47)可知, 只要保证-2aV+(3n-ε)/2 < 0, 即李氏函数的导数负定, 因此满足李雅普诺夫意义下的稳定, 定理2得证.
当
为验证本方法的可行性和优越性, 同时考虑工程应用, 采用工程中系统阶次较高的4阶飞行器位置系统[16]作被控对象, 设计控制器并进行验证仿真.
| $ \left. {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot \xi }} = \mathit{\boldsymbol{\nu }}}\\ {m\mathit{\boldsymbol{\dot \nu }} = {T_f}{\mathit{\boldsymbol{R}}_{{E_z}}} - mg{\mathit{\boldsymbol{E}}_z} + {\mathit{\boldsymbol{d}}_1}}\\ {\mathit{\boldsymbol{\dot \eta }} = W(\mathit{\boldsymbol{\eta }})\mathit{\boldsymbol{w}}}\\ {\mathit{\boldsymbol{J\dot w}} = - \mathit{\boldsymbol{w}} \times \mathit{\boldsymbol{Jw}} + {\mathit{\boldsymbol{\tau }}_f} + {\mathit{\boldsymbol{d}}_2}} \end{array}} \right\} $ |
其中:ξ=[x y z]T表示四旋翼飞行器在惯性系下的位置;ν=[νx νy νz]T表示四旋翼飞行器在惯性系下的线速度;η=[ϕ θ ψ]T表示四旋翼飞行器姿态的欧拉角;w=[p q r]T表示四旋翼飞行器在机体坐标系下的角速度.
设定期望位置为[3 3 2]T, 并设定偏航角期望为0, 定义如下轨迹误差:
| $ \mathit{\boldsymbol{\tilde \xi }} = \mathit{\boldsymbol{\xi }} - {\mathit{\boldsymbol{\xi }}^*} $ |
| $ \mathit{\boldsymbol{\tilde v}} = \mathit{\boldsymbol{v}} - {\mathit{\boldsymbol{v}}^c} $ |
| $ \mathit{\boldsymbol{\tilde \eta }} = \mathit{\boldsymbol{\eta }} - {\mathit{\boldsymbol{\eta }}^c} $ |
| $ \mathit{\boldsymbol{\tilde w}} = \mathit{\boldsymbol{w}} - {\mathit{\boldsymbol{w}}^c} $ |
其中:ξc为期望位置;νc为期望线速度;ηc为期望欧拉角;wc为期望机体角速度.
飞行器的初始位置和初始姿态设定为
| $ \mathit{\boldsymbol{\xi }}(0) = {\left[ {\begin{array}{*{20}{l}} 0&0&0 \end{array}} \right]^{\rm{T}}} $ |
| $ \mathit{\boldsymbol{\eta }}(0) = {\left[ {\begin{array}{*{20}{l}} 0&0&5 \end{array}} \right]^{\rm{T}}} $ |
四旋翼飞行器的期望位置和期望偏航角设定为
| $ {\mathit{\boldsymbol{\xi }}^c}(t) = {\left[ {\begin{array}{*{20}{l}} 3&3&2 \end{array}} \right]^{\rm{T}}} $ |
| $ {\mathit{\boldsymbol{\psi }}^c}(t) = 0 $ |
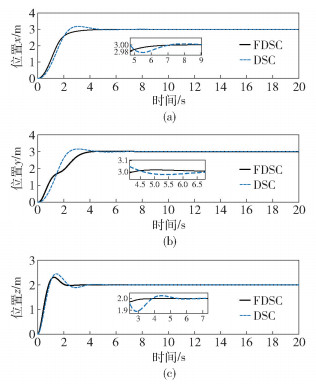
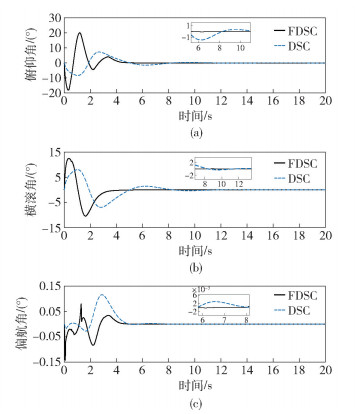
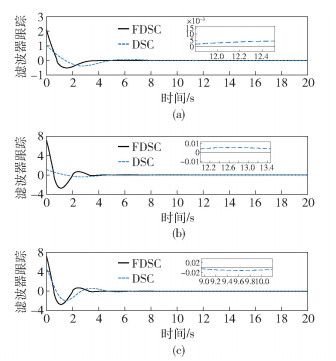
基于期望和条件, 获得的仿真结果如图 1~图 3所示. 图 1为飞行器x、y、z 3个方向的位置响应曲线. 图 2为横滚角、俯仰角、偏航角的姿态响应曲线. 图 3所示为一阶低通滤波器和有限时间滤波器在位置跟踪中的滤波误差收敛对比.由图 1、图 2可知, 笔者设计的控制器与用动态面方法设计的控制器相比具有收敛速度快、稳态误差小的优点.由图 3可以看出,笔者设计的有限时间滤波器与传统一阶低通滤波器相比较具有跟踪输入速度快、且稳定跟踪后, 跟踪误差小的优点.
|
图 1 位置响应曲线 |
|
图 2 姿态角响应曲线 |
|
图 3 滤波器跟踪曲线 |
结合快速终端滑模控制中的滑模面函数和动态面控制技术,研究了高阶非线性系统的镇定和跟踪问题.通过使用在全域内均具有快速有限时间收敛能力的新型滤波器代替动态面技术中的一阶低通滤波器,降低了滤波误差, 从而有效降低了高阶非线性系统控制中的误差积累, 提高了系统的跟踪性能.利用Lyapunov方法证明了系统闭环的稳定性, 解出了系统的稳态误差.仿真结果表明,笔者提出的新型滤波器的性能与传统一阶线性低通滤波器相比有了大幅度改善, 用新方法设计控制器,其跟踪性能比使用动态面方法更优.
| [1] |
Isidori Alberto. Nonlinear control systems[M]. London: Springer Science and Business Media, 2013: 91-99.
|
| [2] |
Levant A. Sliding order and sliding accuracy in sliding mode control[J]. International Journal of Control, 1993, 58(6): 1247-1263. DOI:10.1080/00207179308923053 |
| [3] |
Krstic M, Kanellakopoulos I, Kokotovic P V. Nonlinear and adaptive control design[M]. New York: Wiley, 1995: 490-491.
|
| [4] |
Ramirez-Rodriguez H, Parra-Vega V, Sanchez-Orta A, et al. Robust backstepping control based on integral sliding modes for tracking of quadrotors[J]. Journal of Intelligent and Robotic Systems, 2014, 73(1-4): 51-66. DOI:10.1007/s10846-013-9909-4 |
| [5] |
Wang Y, Wilson P A, Liu X. Adaptive neural network-based backstepping fault tolerant control for underwater vehicles with thruster fault[J]. Ocean Engineering, 2015(110): 15-24. |
| [6] |
Roy T K. Robust adaptive backstepping speed controller design for a series DC motor[C]//Electrical and Computer Engineering (WIECON-ECE), 2015 IEEE International WIE Conference on.[S.l.]: IEEE, 2015: 243-246.
|
| [7] |
Swaroop D, Hedrick J K, Yip P P, et al. Dynamic surface control for a class of nonlinear systems[J]. IEEE Transactions on Automatic Control, 2000, 45(10): 1893-1899. DOI:10.1109/TAC.2000.880994 |
| [8] |
Xu B, Shi Z, Yang C, et al. Composite neural dynamic surface control of a class of uncertain nonlinear systems in strict-feedback form[J]. IEEE Transactions on Cybernetics, 2014, 44(12): 2626-2634. DOI:10.1109/TCYB.2014.2311824 |
| [9] |
Chen M, Tao G, Jiang B. Dynamic surface control using neural networks for a class of uncertain nonlinear systems with input saturation[J]. IEEE Transactions on Neural Networks and Learning Systems, 2015, 26(9): 2086-2097. DOI:10.1109/TNNLS.2014.2360933 |
| [10] |
Pan Y, Yu H. Composite learning from adaptive dynamic surface control[J]. IEEE Transactions on Automatic Control, 2016, 61(9): 2603-2609. DOI:10.1109/TAC.2015.2495232 |
| [11] |
Pan Y, Yu H. Dynamic surface control via singular perturbation analysis[J]. Automatica, 2015(57): 29-33. |
| [12] |
Du J, Abraham A, Yu S, et al. Adaptive dynamic surface control with Nussbaum gain for course-keeping of ships[J]. Engineering Applications of Artificial Intelligence, 2014(27): 236-240. |
| [13] |
Peng Z, Wang D, Wang J. Predictor-based neural dynamic surface control for uncertain nonlinear systems in strict-feedback form[J]. IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(9): 2156-2167. |
| [14] |
Wang Y, Song Y. Fraction dynamic surface based neuroadaptive finite-time containment control of multiagent systems in nonaffine pure-feedback form[J]. IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(3): 678-689. DOI:10.1109/TNNLS.2015.2511005 |
| [15] |
X Yu, M Zhihong. Fast terminal sliding-mode control design for nonlinear dynamical systems[J]. IEEE Transactions on Circuits and Systems I:Fundamental Theory and Applications, 2002, 49(2): 261-264. DOI:10.1109/81.983876 |
| [16] |
Liu Yicheng, Ma Junhui, Tu Haiyan. Robust command filtered adaptive backstepping control for a quadrotor aircraft[J]. Journal of Control Science and Engineering, 2018, 1-9. |



