2. 中国人民解放军31617部队, 福州 350200;
3. 重庆大学 材料科学与工程学院, 重庆 400030
为了提高一致性模糊图像盲复原清晰度,针对复原过程中涉及的全变差模型先验约束问题,提出一种基于先验优化的一致性模糊盲复原算法.利用基于半高斯梯度算子的局部加权全变差模型提取模糊图像显著边缘,在去除噪声和纹理干扰的同时,可提高有利信息的保持能力;提出多尺度混合特性先验估计模糊核,增强了模糊核估计的准确性;利用非盲去卷积得到了清晰的复原图像.实验结果表明,相较其他算法,针对模拟模糊图像,所提算法的复原图像峰值信噪比平均提升约1.7%,结构相似性指数平均提升约19.1%;针对真实模糊图像,复原图像伪影更少,边缘纹理细节更加清晰自然,整体视觉效果更好.
2. No. 96215 Unit of People's Liberation Army, Fuzhou 350200, China;
3. College of Materials Science and Engineering, Chongqing University, Chongqing 400030, China
In order to improve the clarity of the blind restoration of the conformance fuzzy image, a prior fuzzy blind restoration algorithm based on the prior optimization is proposed for the study of the prior constraint problem of the full variational model involved in the restoration process. Firstly, the local weighted total variation model based on half Gauss gradient operator is used to extract the significant edge of the blurred image. The noise and texture interference are removed, and the ability to maintain the favorable information is improved. Then a multi-scale mixed characteristic prior estimation of blur kernel is proposed to enhance the accuracy of blur kernel estimation. Finally, clear restored images are obtained by non-blind deconvolution. The experimental results show that compared with other algorithms, the proposed algorithm improves the average peak signal to noise ratio of the reconstructed image by about 1.7%, and the average structure similarity index increases by about 19.1%. In view of the real blur image, the artifact of restored image is less, the edge texture details are more clear and natural, and the overall visual effect is better.
一致性模糊盲复原是图像复原领域研究的基础性课题之一,主要解决模糊核未知的条件下,空间位移不变模糊图像的清晰复原问题[1].准确高效地从模糊退化模型中恢复出理想清晰图像是盲复原研究的关键[2],正则化方法利用先验特性构造正则项,约束代价函数的求解过程,可以有效解决盲复原中涉及的各类不适定性问题,使得到的解最大程度逼近理想结果[3].由于盲复原算法步骤较多,且模型构造复杂,需要多种先验条件混合约束进行求解,因此研究一种基于正则化的一致性模糊盲复原算法具有重要意义.
在基于正则化的一致性模糊盲复原方面,学者做了大量工作,改进方法大体可分为两类:一类为改进模糊核估计的方法.该类方法通过提高模糊核估计的准确性,间接增强图像复原质量. Fergus等[4]提出基于多尺度空间的模糊核估计算法. Cho等[5]提出基于强边缘的模糊核估计算法. Xu等[6-7]提出基于梯度信息筛选的模糊核估计算法. Ohkoshi等[8]提出基于结构纹理分解的模糊核估计算法. Pan等[9]提出利用局部加权全变差模型(LWTV, local weighted total variation)进行结构纹理分解.另一类为改进非盲去卷积的方法.该类方法通过降低去卷积过程中病态特征的影响,直接增强图像复原质量. Fergus等[4]在估计出模糊核后利用Richardson-Lucy(RL)算法对模糊图像进行非盲复原. Shan等[10]提出利用一种连续分段函数来近似自然图像梯度的重尾分布特性,在迭代的过程中丰富复原图像的边缘细节. Krishnan等[11]提出基于超拉普拉斯的复原算法.通过对比分析,发现相较于分段函数、高斯函数、拉普拉斯函数,利用超拉普拉斯函数可以更好地拟合图像梯度的重尾分布.唐等[12]提出基于多正则化混合约束的复原算法.在复原图像模型重尾特性约束的基础上加入一种有利于边缘锐化的保边正则项进行混合约束. Zhang等[13]提出基于深度卷积神经网络(DCNN, deep convolution neural network)先验的复原算法.通过卷积神经网络利用大量的样本数据,学习模糊图像到清晰图像之间的映射关系,以此作为DCNN先验正则项约束图像非盲复原过程.
上述图像盲复原算法针对算法的不同步骤进行了优化与创新,但仍存在以下问题:1)图像结构提取过程仍不够细化,自适应权重系数有待改进;2)模糊核估计精度不足,先验正则项构造仍需进一步优化.针对以上问题,提出基于先验优化的一致性模糊盲复原算法.
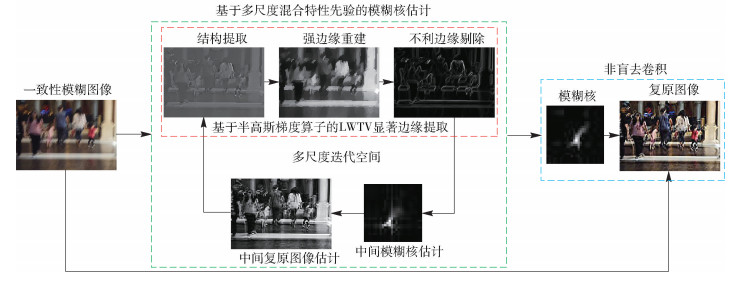
1 算法流程基于正则化的一致性模糊盲复原算法包括显著边缘提取、模糊核估计和非盲去卷积3个主要部分,笔者针对各部分存在的约束不足的问题,分别进行了改进与优化,提出的算法流程如图 1所示.
|
图 1 算法流程 |
步骤1 显著边缘提取.提出基于半高斯梯度算子的LWTV显著边缘提取算法,依次经过结构提取、强边缘重建和不利边缘剔除得到有利的强边缘,作用于模糊核模型保真正则项.
步骤2 模糊核估计.提出基于多尺度混合特性先验的模糊核估计算法,估计模糊核.
步骤3 非盲去卷积.在得到模糊核后,利用文献[13]的非盲去卷积算法,得到最终的清晰复原图像.
2 基于半高斯梯度算子的LWTV显著边缘提取首先利用带方向的半高斯梯度算子计算梯度幅值,其定义为
| $ h(x)=g_{r}\left(\varphi\left(\boldsymbol{R}_{x}\right)\right)-g_{l}\left(\varphi\left(\boldsymbol{L}_{x}\right)\right) $ | (1) |
| $ \alpha_{x}=\arctan \left(\frac{u_{y}(x)}{u_{x}(x)}\right) $ | (2) |
| $ u(x)=g_{r}\left(\boldsymbol{R}_{x}\right)-g_{l}\left(\boldsymbol{L}_{x}\right) $ | (3) |
其中:h表示带方向的半高斯梯度幅值,Rx和Lx分别表示以像素x为中心,半径为η的圆形窗口的左、右半部分,g表示窗口内像素高斯滤波的结果,φ表示角度旋转算子,其偏转角度α如式(2)所示,u表示传统半高斯梯度幅值.
然后将归一化后的h值通过非线性变化得到权重模型,进而提取模糊图像或中间复原图像的结构信息,具体过程如下所示:
| $ \boldsymbol{L}_{L}=\underset{\boldsymbol{L}_{L}}{\arg \min }\left(\left\|\nabla \boldsymbol{L}_{L}\right\|_{2}+\frac{1}{2 \theta \omega(x)}\left\|\boldsymbol{L}_{L}-\boldsymbol{L}^{*}\right\|_{2}^{2}\right) $ | (4) |
| $ \omega(x)=\exp \left(-\|1-h(x)\|^{0.8}\right) $ | (5) |
其中:LL表示图像结构信息,ω(x)表示权重模型,θ为平滑系数,L*为中间复原图像.
随后利用冲击滤波器重建结构图像强边缘.
最后依据文献[6]所提理论,结合估计的模糊核尺寸对不利边缘进行剔除,得到显著边缘LSL.
3 基于多尺度混合特性先验的模糊核估计1) 尺度空间构建
尺度空间一般由组与层构成,逐组降采样,逐层模型估计.根据估计的模糊核尺寸,具体公式为
| $ O=\max \left(\left\lfloor\frac{\ln (5 / \min (m, n))}{\ln (r)}\right\rfloor_{\operatorname{floor}}, 0\right)+1 $ | (6) |
其中:m和n表示模糊核尺寸大小,r表示降采样因子,
2)模糊核模型构建
将提取到的显著边缘LSL作用于保真项,然后采用超拉普拉斯函数拟合稀疏先验分布,最后利用模糊核梯度的范数保证平滑特性,模型的表达式为
| $ \begin{aligned} \hat{\boldsymbol{k}}=& \underset{\boldsymbol{k}}{\arg \min }\left(\frac{1}{2}\left\|\nabla \boldsymbol{L}_{\text {SL }} \boldsymbol{k}-\nabla \boldsymbol{B}\right\|_{2}^{2}+\right.\\ &\left.\lambda_{k 1}\|\boldsymbol{k}\|_{p}^{p}+\lambda_{k 2}\|\nabla \boldsymbol{k}\|_{2}^{2}\right) \end{aligned} $ | (7) |
其中:k为模糊核,B为模糊图像,LSL为显著边缘图像,‖k‖pp为稀疏正则项,‖∇k‖22为平滑正则项.
式(7)为约束最优化问题,笔者利用半二次分裂策略,引入惩罚函数‖b1-k‖22,使其转化为非约束最优化问题,即
| $ \begin{array}{l}{\left(\hat{\boldsymbol{k}}, \hat{\boldsymbol{b}}_{1}\right)=\underset{\boldsymbol{k}, \boldsymbol{b}_{1}}{\arg \min }\left(\frac{1}{2}\left\|\nabla \boldsymbol{L}_{\mathrm{SL}} \boldsymbol{k}-\nabla \boldsymbol{B}\right\|_{2}^{2}+\right.} \\ {\left.\lambda_{k 1}\left\|\boldsymbol{b}_{1}\right\|_{p}^{p}+\frac{\gamma_{k}}{2}\left\|\boldsymbol{b}_{1}-\boldsymbol{k}\right\|_{2}^{2}+\lambda_{k 2}\|\nabla \boldsymbol{k}\|_{2}^{2}\right)}\end{array} $ | (8) |
式(8)可转化为如下迭代的子问题:
| $ \begin{aligned} \boldsymbol{k}^{i+1} &=\underset{\boldsymbol{k}}{\arg \min }\left(\frac{1}{2}\left\|\nabla \boldsymbol{L}_{\mathrm{SL}} \boldsymbol{k}-\nabla \boldsymbol{B}\right\|_{2}^{2}+\right.\\ &\left.\frac{\gamma_{k}}{2}\left\|\boldsymbol{b}_{1}-\boldsymbol{k}\right\|_{2}^{2}+\lambda_{k 2}\|\nabla \boldsymbol{k}\|_{2}^{2}\right) \end{aligned} $ | (9) |
| $ \boldsymbol{b}_{1}^{i+1}=\underset{\boldsymbol{b}_{1}}{\arg \min }\left(\frac{\gamma_{k}}{2}\left\|\boldsymbol{b}_{1}-\boldsymbol{k}\right\|_{2}^{2}+\lambda_{k 1}\left\|\boldsymbol{b}_{1}\right\|_{p}^{p}\right) $ | (10) |
式(9)为k的二次函数,可利用二维快速傅里叶变换求得封闭解:
| $ \begin{array}{l} {\mathit{\boldsymbol{k}}^{i + 1}} = {F^{ - 1}}\\ \left( {\frac{{\bar F\left( {{\nabla _h}\mathit{\boldsymbol{L}}_{{\rm{SL}}}^i} \right) \circ F\left( {{\nabla _h}\mathit{\boldsymbol{B}}} \right) + \bar F\left( {{\nabla _v}\mathit{\boldsymbol{L}}_{{\rm{SL}}}^i} \right) \circ F\left( {{\nabla _v}\mathit{\boldsymbol{B}}} \right) + {\gamma _k}F\left( {\mathit{\boldsymbol{b}}_1^i} \right)}}{{{\gamma _k} + \bar F\left( {{\nabla _h}\mathit{\boldsymbol{L}}_{{\rm{SL}}}^i} \right) \circ F\left( {{\nabla _h}\boldsymbol{L}_{{\rm{SL}}}^i} \right) + \bar F\left( {{\nabla _v}\mathit{\boldsymbol{L}}_{{\rm{SL}}}^i} \right) \circ F\left( {{\nabla _v}\boldsymbol{L}_{{\rm{SL}}}^i} \right) + 2{\lambda _{k2}}\left( {\bar F{\left( {{\nabla _h}} \right) \circ F\left( {{\nabla _h}} \right) + \bar F\left( {{\nabla _v}} \right) \circ F\left( {{\nabla _v}} \right)} } \right)}}} \;\;\;\;\;\right) \end{array} $ | (11) |
其中:F为快速傅里叶变换,F-1为其逆变换,F为其复共轭,i为迭代次数.
在p值固定的情况下,式(10)可通过查表法快速得到近似解.
3) 复原图像模型构建
将得到的模糊核代入保真项,然后采用超拉普拉斯函数拟合清晰图像的重尾先验特性,模型的表达式为
| $ \hat{\boldsymbol{L}}=\underset{\boldsymbol{L}}{\arg \min }\left(\frac{1}{2}\|\boldsymbol{L} \boldsymbol{k}-\boldsymbol{B}\|_{2}^{2}+\lambda_{L}\|\nabla \boldsymbol{L}\|_{p}^{p}\right) $ | (12) |
其中:‖∇L‖pp为超拉普拉斯先验项,λL为先验项系数.
式(12)的求解同式(7),引入惩罚函数‖b2-∇L‖22,其求解过程如下:
| $ \begin{array}{c}{\left(\hat{\boldsymbol{L}}, \hat{\boldsymbol{b}}_{2}\right)=\underset{\boldsymbol{L}, \boldsymbol{b}_{2}}{\arg \min }\left(\frac{1}{2}\|\boldsymbol{L} \boldsymbol{k}-\boldsymbol{B}\|_{2}^{2}+\right.} \\ {\left.\lambda_{L}\|\nabla \boldsymbol{L}\|_{p}^{p}+\frac{\gamma_{u}}{2}\left\|\boldsymbol{b}_{2}-\nabla \boldsymbol{L}\right\|_{2}^{2}\right)}\end{array} $ | (13) |
| $ \boldsymbol{L}^{i+1}=\underset{\boldsymbol{L}}{\arg \min }\left(\frac{1}{2}\|\boldsymbol{L} \boldsymbol{k}-\boldsymbol{B}\|_{2}^{2}+\frac{\gamma_{u}}{2}\left\|\boldsymbol{b}_{2}-\nabla \boldsymbol{L}\right\|_{2}^{2}\right) $ | (14) |
| $ \boldsymbol{b}_{2}^{i+1}=\underset{\boldsymbol{b}_{2}}{\arg \min }\left(\lambda_{L}\|\nabla \boldsymbol{L}\|_{p}^{p}+\frac{\gamma_{u}}{2}\left\|\boldsymbol{b}_{2}-\nabla \boldsymbol{L}\right\|_{2}^{2}\right) $ | (15) |
| $ \begin{array}{c} {L^{i + 1}} = \\ {F^{ - 1}}\left( {\frac{{\bar F\left( {{k^{i + 1}} \circ F(\mathit{\boldsymbol{B}}) + {\gamma _u}\left( {\bar F\left( {{\nabla _h}} \right) \circ F\left( {\mathit{\boldsymbol{b}}_{2h}^i} \right) + \bar F\left( {{\nabla _v}} \right) \circ F\left( {\mathit{\boldsymbol{b}}_{2v}^i} \right)} \right)} \right.}}{{\bar F\left( {{\mathit{\boldsymbol{k}}^{i + 1}}} \right) \circ F\left( {{\mathit{\boldsymbol{k}}^{i + 1}}} \right) + {\gamma _u}\left( {\bar F\left( {{\nabla _h}} \right) \circ F\left( {{\nabla _h}} \right) + \bar F\left( {{\nabla _v}} \right) \circ F\left( {{\nabla _v}} \right)} \right)}}} \;\;\;\;\right) \end{array} $ | (16) |
1) 实验数据
实验采用模拟模糊图像和自然真实模糊图像验证算法的鲁棒性与实用性.模拟模糊图像取自威茨曼大学Anat Levin教授提供的公开模糊数据集,包括4幅清晰图像(Kid、House、Wall、Smile)和8种模糊核,如图 2所示.真实模糊图像如图 3所示,具有不同的场景和模糊程度,可以较好的验证算法的实用性.

|
图 2 模拟模糊数据集 |

|
图 3 真实模糊数据集 |
2) 评价指标
峰值信噪比(PSNR, peak signal to noise ratio)主要是衡量算法的去噪能力,值越大表明算法的去噪能力越强.
结构相似性指数(SSIM, structural similarity index measure)是图像结构信息相似度的指标,值越大复原图像失真度越小.
3) 实验过程
实验1 本文算法与传统算法的鲁棒性对比.利用文献[5, 6, 9]算法和本文算法对模拟模糊图像进行复原实验,通过2种有参考评价指标对各算法复原图像质量进行评价,以验证本文算法的鲁棒性.
实验2 本文算法有效性测试.利用文献[6]算法、文献[9]算法和本文算法对真实模糊图像进行图像复原实验,通过主观视觉效果对比验证本文所提算法的有效性.
4.2 结果分析
|
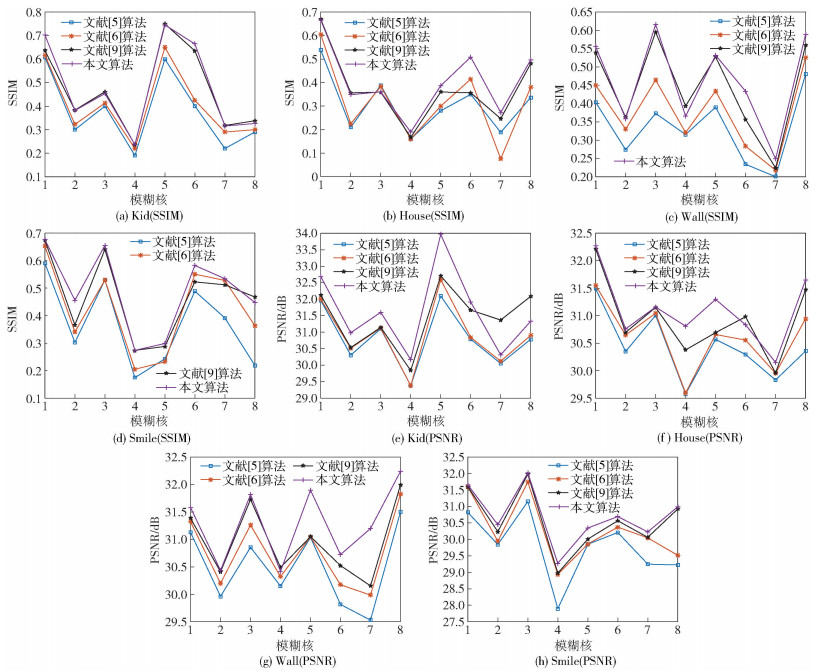
图 4 模拟模糊图像复原效果的定量比较 |
|
|
表 1 复原图像评价指标均值对比 |
实验1结果分析如下:
1) 通过对模拟模糊复原图像的PSNR、SSIM两个定量指标的对比可知,针对不同的图像和模糊核,与其他先进复原算法相比,本文算法复原图像与原始清晰图像的相似度更高,去噪性能较强,整体复原效果较优;
2) 由表 1分析可知,在本文实验环境下,本文算法的PSNR平均提升约1.7%,SSIM平均提升约19.1%.
实验2中真实模糊图像的复原效果如图 5所示,其中,右下方叠加图像为局部细节特写.通过主观视觉对比,本文算法相较其他算法复原图像伪影更少,边缘纹理细节更加清晰、自然,具有更强实用性.

|
图 5 真实模糊图像复原效果的定性比较 |
提出一种基于先验优化的一致性模糊盲复原算法,并通过理论与实验验证了算法的可行性与优势.主要得到以下结论:
1) 利用模型优化LWTV对模糊图像进行显著边缘检测,可细化结构提取过程,提高有利信息的保持能力;
2) 利用多尺度混合特性先验估计模糊核,可使模糊核估计更加准确;
3) 在本文实验环境下,相较其他先进算法,本文算法不仅可以更好地去除模糊,并且可以有效保留图像的边缘细节和纹理特征;
4) 本文算法在图像复原、人工智能、摄影测量等多个领域,具有广阔的应用前景;
5) 模糊核空间变化的非一致性模糊图像复原将是下一步的研究重点.
| [1] |
孙士洁, 赵怀慈, 李波, 等. 利用低秩先验的噪声模糊图像盲去卷积[J]. 电子与信息学报, 2017, 39(8): 1919-1926. Sun S J, Zhao H C, Li B, et al. Blind deconvolution for noisy and blur images using low rank prior[J]. Journal of Electronics and Information Technology, 2017, 39(8): 1919-1926. |
| [2] |
You Y L, Kaveh M. A regularization approach to joint blur identification and image restoration[J]. IEEE Transactions on Image Processing, 1996, 5(3): 416-428. |
| [3] |
唐述, 龚卫国, 仲建华. 稀疏平滑特性的多正则化约束图像盲复原方法[J]. 软件学报, 2013, 24(5): 1143-1154. Tang S, Gong W G, Zhong J H. Sparsity and smoothing multi-regularization constraints for blind image deblurring[J]. Journal of Software, 2013, 24(5): 1143-1154. |
| [4] |
Fergus R, Singh B, Hertzmann A, et al. Removing camera shake from a single photograph[J]. ACM Transactions on Graphics, 2006, 25(3): 787-794. DOI:10.1145/1141911.1141956 |
| [5] |
Cho S, Lee S. Fast motion deblurring[J]. ACM Transactions on Graphics, 2009, 28(5): 1-8. |
| [6] |
Xu L, Jia J. Two-phase kernel estimation for robust motion deblurring[C]//Computer Vision-ECCV 2010, European Conference on Computer Vision, Heraklion, Crete. Greece: [s.n.], 2010: 157-170. https://link.springer.com/chapter/10.1007/978-3-642-15549-9_12
|
| [7] |
Xu L, Zheng S, Jia J. Unnatural L0 sparse representation for natural Image deblurring[C]//Computer Vision and Pattern Recognition.[S.l.]: IEEE, 2013: 1107-1114. https://ieeexplore.ieee.org/document/6618991
|
| [8] |
Ohkoshi K, Sawada M, Goto T, et al. Blind image restoration based on total variation regularization and shock filter for blurred images[C]//IEEE International Conference on Consumer Electronics.[S.l.]: IEEE, 2014: 217-218. https://ieeexplore.ieee.org/document/6775979
|
| [9] |
Pan J, Liu R, Su Z, et al. Kernel estimation from salient structure for robust motion deblurring[J]. Signal Processing Image Communication, 2013, 28(9): 1156-1170. DOI:10.1016/j.image.2013.05.001 |
| [10] |
Shan Q, Jia J, Agarwala A. High-quality motion deblurring from a single image[J]. ACM Transactions on Graphics, 2008, 27(3): 1-10. |
| [11] |
Krishnan D, Fergus R. Fast image deconvolution using hyper-Laplacian priors[C]//Proceedings of the 23rd Annual Conference on Neural Information Processing Systems. Vancouver: NIP, 2009: 1033-1041. https://www.mendeley.com/catalogue/mrabased-wavelet-frames-applications/
|
| [12] |
唐述, 谢显中. 多正则化混合约束的模糊图像盲复原方法[J]. 电子与信息学报, 2015, 37(4): 770-776. Tang S, Xie X Z. Multi-regularization hybrid constraints method for blind image restoration[J]. Journal of Electronics and Information Technology, 2015, 37(4): 770-776. |
| [13] |
Zhang K, Zuo W, Gu S, et al. Learning deep CNN denoiser prior for image restoration[C]//Computer Vision and Pattern Recognition.[S.l.]: IEEE, 2017: 2808-2817. https://ieeexplore.ieee.org/document/8099783
|



