2. 南昌航空大学 信息工程学院, 南昌 330063
评估机会网络的关键节点可以发现对网络吞吐量影响最大的节点,为网络的优化和维护提供支撑.为此,针对机会网络拓扑结构动态变化的特性构建了拓扑凝聚图,定义了二阶节点度、连接强度和关键域重要度3个评估指标,以指标的欧式距离表征节点的重要性.实验结果表明,与介数中心性方法相比,提出的模型具有有效性和优越性,并且模型在时间窗取20 min时具有较高的精度.
2. School of Information Engineering, Nanchang Hangkong University, Nanchang 330063, China
By evaluating critical nodes of opportunistic networks, it was found the nodes that have the greatest influence on the throughput of network, which can support for network optimization and maintenance. The topological condensation graph was constructed according to the characteristics of frequent topology changes in opportunistic networks, and three evaluation metrics, such as second-order degree, connection strength, and key domain importance, were defined. The Euclidean distance of the metrics was employed to characterize the importance of the nodes. Experiments show that the proposed model is effective and superior compared with the betweenness method, and the model has higher accuracy when the time window is set for 20 minutes.
机会网络是一种不需要源节点与目的节点之间存在稳定链路,利用节点移动带来的相遇机会实现通信的自组织网络[1].机会网络以“存储—携带—转发”的模式传递信息,信息多跳转发时,网络会面临关键节点失效导致网络分割或连通性[2]下降等问题.因此,评估网络中的关键节点对于优化和维护网络,增强网络连通性都具有非常重要的意义.
关键节点评估方法主要包括基于单一参数和基于多参数的方法.基于单一参数的方法有节点收缩[3]等;基于多参数的方法有多属性决策[4]、多参数节点排序[5]、关键区域识别[6]等.但这些大多是针对静态网络,未考虑机会网络的时变性,使得这些指标不再适用于机会网络关键节点的评估.因此,需要根据机会网络的特性构建相应的指标评估关键节点.
针对机会网络的时变性构建拓扑凝聚图模型,刻画动态变化的拓扑;结合机会网络中节点的局部特性、行为特性以及全局特性,定义二阶节点度、连接强度以及关键域重要度3个评估指标,在此基础上采用欧式距离评估机会网络中的关键节点.
1 机会网络的特性从局部特性、行为特性以及全局特性3个方面表征机会网络的特性,在此基础上构建反映节点重要性的评估指标.
1.1 局部特性机会网络的局部特性可用节点的局部连接情况表示.常用节点度表征节点的局部重要性.但节点度反映的仅是邻域内的连接情况,不能表征邻域外的交互情况.当网络中存在“桥节点”或度相同的节点时,节点度无法反映该节点的重要性.因此,可将节点的直接邻居扩展到多跳邻居.机会网络基本不存在端到端的连接,节点间通过移动转发的模式通信,因此,网络中的节点大多处于游离态,只有极少数的节点间存在连接.为降低计算复杂度,考虑节点的2跳邻居,用二阶节点度表征节点的局部重要性,该指标可以识别出“桥节点”的情况.
1.2 行为特性机会网络大多是以人为主体通过携带通讯设备而产生的网络,因而具有一定的社会性.在社会生活中,与他人交互的频率通常可反映出关系的紧密程度.两人联系的次数越多,联系时间越长,说明两人关系越紧密,相互之间越重要.基于图论的相关理论,给节点间的连边赋予一定的权重,表征节点之间的紧密程度,紧密程度越大,连边的权重越大.考虑将某段时间内节点对间发生连接的总次数和总时长的乘积作为节点间连边的权重,用节点与邻居节点的权重之和表征节点的关系特性.
1.3 全局特性机会网络具有一定的社团属性,相比社团内部节点,社团间节点维持不同社团之间的数据传输.这些节点大多处于网络的中心,经过这些节点传递的数据以及传输的路径更多.这些节点发生故障会影响网络的数据传输.介数中心性和接近中心性均能较为准确地发现静态网络中心位置的节点.在对机会网络的动态拓扑进行表示的基础上研究表征节点全局特性的指标.结合机会网络的稀疏性,考虑某个范围内节点的介数中心性和接近中心性,将两者的乘积作为机会网络节点全局特性的一个指标.
2 机会网络关键节点评估方法对机会网络动态变化的拓扑进行表示,结合机会网络的特性构建评估指标,通过建立评估模型对关键节点进行评估,同时给出关键节点评估算法.
2.1 动态拓扑表示机会网络的时变性使得网络的拓扑结构不断变化,准确描述这种变化是评估关键节点的前提.将总时长分割成一系列时间窗口,在每个时间窗口内,将所有发生通信的节点互相连接起来,即将时间窗口内的动态拓扑凝聚成一系列静态网络拓扑图.
定义1 拓扑凝聚图
拓扑凝聚图集合G={G1, G2, …, Gn}是一系列时间窗口(t0, t1], (t1, t2], …, (tn-1, tn]的有序图集, 且(t0, tn]=T,(t0, t1]=(t1, t2]=… =(tn-1, tn]=Δt,Gi=(Vi, Ei, ωi)表示时间窗口(ti-1, ti]内的拓扑凝聚图,即第i个时间窗口内节点间边的凝聚结果,Vi为该时间窗口内的节点集合,Ei为该时间窗口内发生连接的节点间边的集合,ωi为边集Ei各边的权值所构成的集合.
定义2 拓扑凝聚图权值
在拓扑凝聚图Gi=(Vi, Ei, ωi)中,节点对之间边的权值集合ωi定义为该时间窗口内节点对之间连接次数与连接时长之积,定义为
| $ \begin{array}{c} \omega_{i}:=\{\omega_{a b}^{i}=H \sum\limits_{k=1}^{H}\left(t_{k-\text { end }}^{a b}-t_{k-\text { stant }}^{a b}\right) | \forall a, \\ b \in V(a \neq b) \wedge(a, b) \in E , \\k \in N^{*}, H \in N\} \end{array} $ | (1) |
其中:ωabi为第i个拓扑凝聚图中节点a与b之间边的权值,H为第i个时间窗口内节点a与b建立连接的次数,k为节点a与b第k次建立连接,tk-endab为节点a与b第k次连接断开的时刻,tk-startab为节点a与b第k次连接开始的时刻.
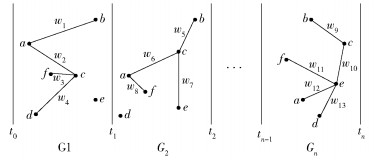
根据定义1和定义2,可以对机会网络的动态拓扑进行表示,得到如图 1所示的模型.
|
图 1 机会网络拓扑凝聚图 |
用二阶节点度、连接强度以及关键域重要度3个评估指标表征节点在机会网络中的重要程度,定义如下.
定义3 二阶节点度
给定拓扑凝聚图集合G={G1, G2, …, Gn},在拓扑凝聚图Gi中,任意节点a的邻域为αa,即与节点a邻接的节点集合,αa={b|(a, b)∈E},b是a的邻接节点,设b的节点度为Kb, 定义节点a的二阶节点度为
| $ D_{a}=\sum\limits_{b \in \alpha_{a}} K_{b} $ | (2) |
节点a的二阶节点度不仅能反映节点a与邻接节点间通信的情况,而且能够体现与a不直接相邻的节点与节点a间接通信的情况.
定义4 连接强度
在拓扑凝聚图Gi中,任意节点a的连接强度定义为与节点a连接的所有边的权值之和,节点a的连接强度定义为
| $ Q_{a}=\sum\limits_{b \in \alpha_{a}} \omega_{a b} $ | (3) |
其中ωab为节点a和b连边的权值.
连接强度反映了目标节点与周围节点相互通信的紧密程度,某个节点的连接强度越大,则该节点作为局部网络枢纽的可能性越大.
定义5 关键域重要度
在节点a的邻域αa中,任意2个节点h、j的邻域分别为αh、αj,定义a的关键域为Fa={s|s∈(αh∩αj)∪αa, s≠a},Ba表示Fa中任意节点对之间不经过a的最短路径数,Sa表示Fa中任意节点对之间经过a的最短路径数.设a的节点度为Ka,基于关键域节点a的介数定义为
| $ G_{a}=\left\{\begin{array}{l}{0, \quad K_{a}=1} \\ {\frac{S_{a}}{S_{a}+B_{a}}, \quad K_{a} \geqslant 2}\end{array}\right. $ | (4) |
Fa中节点a到b的长度(最短跳数)用d(a, b)表示,基于关键域的节点a的接近度定义为
| $ C_{a}=\frac{1}{\sum\limits_{b \in F_{a}} d(a, b)}, a \neq b $ | (5) |
定义节点a的关键域重要度为
| $ I_{a}=G_{a} C_{a} $ | (6) |
节点的关键域重要度越大,表明节点位于网络中心的可能性越大,节点越重要.
2.3 关键节点评估模型从多个角度考虑机会网络的特点,建立了反映节点重要性的3个评估指标,提出基于欧式距离的评估模型,综合考虑节点的二阶节点度、连接强度以及关键域重要度评估机会网络中的关键节点.
给定节点的二阶节点度Da、连接强度Qa以及关键域重要度Ia,将这3个指标归一化后,定义节点a的欧式距离,即评估模型为
| $ U_{a}=\sqrt{\left\|D_{a}\right\|^{2}+\left\|Q_{a}\right\|^{2}+\left\|I_{a}\right\|^{2}} $ | (7) |
节点的模型值越大,则该节点成为关键节点的可能性越大.
2.4 关键节点评估算法的设计评估机会网络关键节点的算法如下.
算法1 基于拓扑凝聚图的机会网络关键节点评估算法
输入:数据集U,时间窗口Δt,总时长T.
输出:关键节点的编号.
步骤1 用Δt对T切片,建立第一个时间窗口内的拓扑凝聚图模型,获取节点的评估指标值.
步骤2 对3个评估指标值归一化处理后作为评估模型的输入,输出得到节点的模型值,模型值最大的节点为疑似关键节点.
步骤3 重复实验步骤1~2,获取其余时间窗口内的疑似关键节点编号.
步骤4 统计每个节点被判定为疑似关键节点的次数,并按由大到小的顺序排列.
步骤5 输出排序靠前的节点编号.
3 仿真实验设计与分析设计不同场景和时间窗口下的对比仿真实验,与目前常用的介数中心性方法对比验证本文评估模型的合理性和有效性.
3.1 仿真实验设计采用机会网络环境模拟器(ONE,opportunistic network environment)进行仿真实验,设置3个不同的实验场景获取仿真实验数据集,数据集格式为:节点ID、节点ID、连接开始时刻、连接结束时刻.使用Matlab2014a对数据集进行分析处理.仿真实验参数设置见表 1,其中,区域内节点的移动模型为随机路径点(RWP,RandomWayPoint),区域间节点的移动模型为基于地图移动(MBM,map based movement).
|
|
表 1 仿真实验参数设置 |
关键节点失效会导致网络分割,从网络分割程度不同的角度评估关键节点.考虑关键节点失效导致网络某个区域分割的情况,设置实验场景1;考虑关键节点失效导致网络多个区域分割的情况,设置实验场景2;考虑关键节点失效导致网络所有区域分割的情况,设置实验场景3.
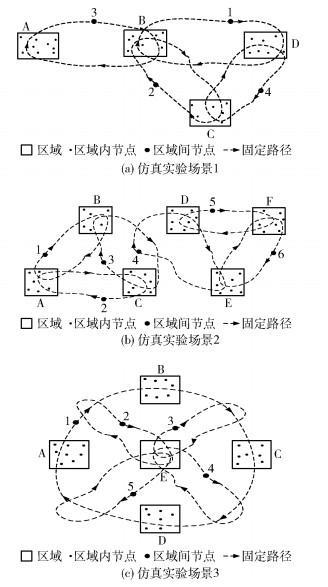
仿真实验场景如图 2所示,设置如下.
|
图 2 关键节点仿真实验场景 |
1) 场景1:包含A~D共4个区域,区域内部节点随机移动,区域之间有1~4号共4个节点按固定路径移动,如图 2(a)所示.
2) 场景2:包含A~F共6个区域,区域内部节点随机移动,区域之间有1~6号共6个节点按固定路径移动,如图 2(b)所示.
3) 场景3:包含A~E共5个区域,区域内部节点随机移动,有1~5号共5个节点按固定路径移动,如图 2(c)所示.
3.2 实验结果及分析由于区域内部节点随机游走,且节点密度和通信半径都较大,故暂不考虑区域内部节点,网络的关键节点从区域间的节点中产生. 3个场景下,每个区域间节点被判定为疑似关键节点次数的统计结果如图 3~5所示.
|
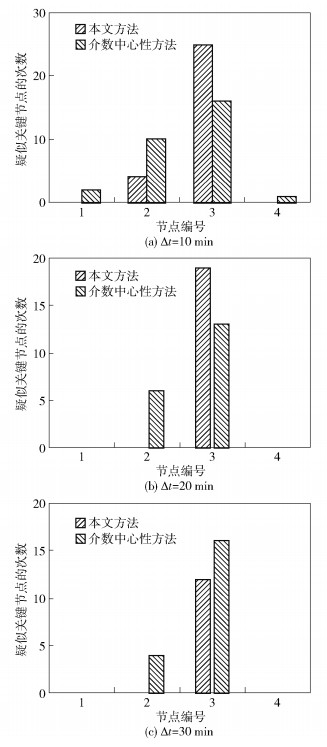
图 3 场景1中疑似关键节点次数统计 |
|
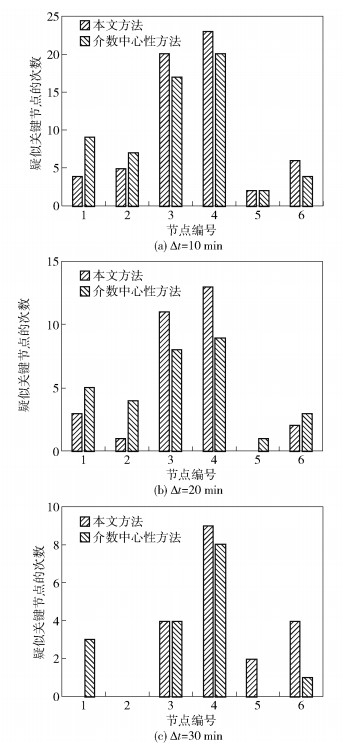
图 4 场景2中疑似关键节点次数统计 |
|
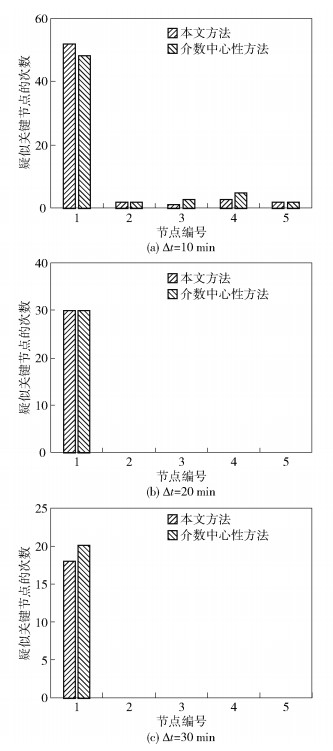
图 5 场景3中疑似关键节点次数统计 |
场景1中,若3号节点失效会使区域A从整网分割出去,故该节点是关键节点.由图 3可知,3号节点的疑似关键节点次数最多,是评估出的关键节点,与实际相符.本文模型中,3号节点在10、20、30 min时的疑似关键节点次数分别为25、19、12,评估准确度分别为41.7%、63.3%、60%.场景2中,若3号或4号节点失效会使网络分割成ABC、DEF两个不连通的区域,故3号和4号节点是关键节点,与图 4显示的评估结果一致.本文模型中,3号和4号节点在10、20、30 min时的疑似关键节点次数分别为43、24、13,评估准确度分别为71.7%、80%、65%.场景3中,1号节点失效会导致网络所有区域产生分割,该节点是关键节点,与评估结果一致.本文模型中,1号节点在10、20、30 min时的疑似关键节点次数分别为52、30、18,评估准确度分别为86.6%、100%、90%.
不同时间窗下的对比实验结果表明: 20 min比10 min情况下的准确度更高,30 min时的准确度有所下降,且低于介数中心性方法.这是由于随着时间窗的增大,时间窗口内节点间的连接更密集,将其作为一个时间切片计算各个指标的值,不符合机会网络连接稀疏性的特点,导致评估结果的准确度有所下降,故时间窗取20 min左右时评估效果较好.
综上所述,这3个场景代表了关键节点失效导致网络分割的典型情况,笔者提出的关键节点评估模型可以准确评估出不同场景下机会网络的关键节点,该模型具有有效性.
4 结束语提出了机会网络关键节点评估指标,通过3个评估指标刻画机会网络运行过程中的节点重要性.与介数中心性方法的对比实验结果验证了评估指标的有效性和优越性.此外,不同时间窗下的实验结果进一步表明,时间窗取20 min时具有较高的评估准确率.下一步考虑将该方法运用到实验床实验中,以验证所提出评估模型的有效性.
| [1] |
姚建盛, 马春光, 袁琪. 基于债务的机会网络"物-物交换"激励机制[J]. 北京邮电大学学报, 2016, 39(4): 103-107. Yao Jansheng, Ma Chunguang, Yuan Qi. A debt-based barter trade incentive mechanism in opportunistic networks[J]. Journal of Beijing University of Posts and Telecommunications, 2016, 39(4): 103-107. |
| [2] |
Gianni F, Pier L. Connectivity analysis of ecological landscape networks by cut node ranking[J]. Applied Network Science, 2018, 3(1): 1-15. |
| [3] |
Yang Y, Xie G. Efficient identification of node importance in social networks[J]. Information Processing and Management, 2016, 52(5): 911-922. DOI:10.1016/j.ipm.2016.04.001 |
| [4] |
Chen Q, Liu L, Yang Z, et al. Prediction approach of critical node based on multiple attribute decision making for opportunistic sensor networks[J]. Journal of Sensors, 2016(4): 1-8. |
| [5] |
张岩, 黄韬, 卢波, 等. 基于多参数节点排序的SDN控制器部署策略[J]. 北京邮电大学学报, 2016, 39(4): 30-34. Zhang Yan, Huang Tao, Lu Bo, et al. SDN controller deployment strategy based on multi-parameter node sorting[J]. Journal of Beijing University of Posts and Telecommunications, 2016, 39(4): 30-34. |
| [6] |
Wang Song, Zhang Tiankui, Feng Chunyan. Nodes and links jointed critical region identification based network vulnerability assessing[C]//IEEE International Conference on Network Infrastructure and Digital Content (IC-NIDC). Beijing: IEEE Press, 2017: 66-71.
|


