2. 公安部第三研究所, 上海 201204
传统的影响力地图或者缺乏对动态信息的表示,或者对动态信息的表示不准确,容易导致游戏人工智能(AI)主体做出错误的决策.为了解决影响力地图不易描述动态信息的问题,对影响力地图的传播方式和衰减方式进行了研究,提出了基于距离调整的动态影响力地图模型.根据产生影响对象的运动趋势,对影响传播过程中需要计算的距离进行调整,将运动趋势信息编码于最终的影响力地图中,为游戏AI主体的决策过程提供支持.实验结果表明,相较于传统影响力地图模型,该模型可以有效提高影响力地图对游戏环境动态信息表示的准确程度,从而提高AI主体的性能.
2. The Third Research Institute of the Ministry of Public Security, Shanghai 201204, China
The traditional influence map either lacks the representation of dynamic information or is inaccurate in the representation, which will easily lead to the wrong decision of the game artificial intelligence subject. In order to solve the problem that influence map was difficult to describe dynamic information, the propagation mode and attenuation mode of influence map were studied, and a dynamic influence map model based on distance adjustment was proposed. According to the movement trend of the objects affected, the distance to be calculated in the process of impact propagation was adjusted The model can encode dynamic information into the influence map so as to support decision making of the game agent. Experiments show that compared with traditional influence map, this model can effectively improve the accuracy of the dynamic information representation in influence map, thus enhance the performance of the game agent.
影响力地图又称势力图,是一种经常被用于游戏人工智能(AI,artificial intelligence)的决策支持技术,最早是从围棋游戏的空间推理工作[1]中演化而来的.影响力地图是AI主体关于游戏世界知识的空间表示,将游戏环境中纷繁复杂的信息用统一的方式进行描述和计算,为AI的决策提供依据.
影响力地图使用网格描述游戏空间中的信息,通过表示特定概念的函数计算网格内的“影响力”,这些概念包括战斗力、脆弱性等.不同的影响力地图相互组合,形成决策空间[2].在二维环境中,影响力地图采用方形或六边形网格进行表示和计算,当某个网格中有一些游戏对象时,会对周围的网格产生影响.某个网格对另一个网格产生的影响力与该网格含有的游戏对象数量和类型以及2个网格间距离相关.影响力地图还可以应用于三维环境中[3].影响力地图经常被用于游戏开发中,如Wirth等[4-5]分别使用了不同的方法,在吃豆人女士游戏中设计了基于影响力地图的决策模型. Miles等[2]将协同进化算法与影响力地图结合,并应用于实时战略游戏中.
在机器人技术中,也有与影响力地图非常相似的概念——势场法(Potential Field)[6].其与影响力地图不同的是,势场法基于欧式距离进行计算,仅对感兴趣的某几个点进行分析,且无法考虑地形问题.
1 相关研究Wirth等[4]使用了线性衰减、欧式距离计算影响力的方式,在吃豆人女士游戏中设计了一个简单的影响力地图模型,通过实验搜索的方式找出了合理的参数范围,并测试了简单的迭代优化算法(爬山算法/贪心算法)在影响力地图参数确定中的作用. Svensson等[5]同样在吃豆人女士游戏中,利用影响力地图设计了决策模型,但其中使用了A*寻路的路径长度作为传播依据,衰减方式为指数衰减,参数确定方式与Wirth等[4]提出的模型相同.相较于Wirth等[4]提出的模型,在精度和性能上有所改善.但这2个模型都仅根据游戏对象的位置进行影响力的传播与计算,未考虑游戏对象的运动信息. Tozour在文献[3]中给出了影响力地图概念,介绍了影响力地图所用到的不同传播方式和衰减方法,并对影响力地图构建提供了一些经验性的指导.其中还介绍了一种使用影响力地图编码动态信息的方法,但这种方法过于简单且不够准确,容易造成局部影响力趋势错误.
2 影响力地图影响力地图计算过程中,针对每个游戏对象,首先在对象所在网格中计算其初始影响力(初始影响力通常根据经验设定或由实验确定),之后将该游戏对象产生的影响传播到周围的网格中.在传播过程中,影响力不是保持不变的,而是会随着与该对象之间的距离增大而逐渐衰减[3].这涉及2个方面的问题:如何度量距离(传播方式);如何根据距离计算影响力(衰减方式).
2.1 影响力衰减方式游戏对象在距离其较近的地方产生的影响力绝对值相对较大,在距离其较远的地方产生的影响力绝对值相对较小,影响力衰减是指影响力绝对值随着距离的增大而减小的过程.影响力绝对值与距离呈负相关关系,常用的衰减方式有线性衰减、指数衰减.通常,一个游戏对象的影响力不会传播到地图的任何地方,而是衰减到一定大小就停止传播[3].
1) 线性衰减
线性衰减中,每增加一个网格长度的距离,影响力衰减一个固定的值.其影响力大小与距离的关系为
| $ I_{p, i}=\left\{\begin{array}{l}{I_{i}-\beta d_{i, p}, } ~~~ {d_{i, p} \leqslant D} \\ {0, } ~~~ {d_{i, p}>D}\end{array}\right. $ | (1) |
其中:Ip, i为游戏对象i对点p产生的影响力,Ii为游戏对象i的初始影响力,β为衰减速度,D为最大传播距离(停止条件),di, p为i与点p之间的距离.
2) 指数衰减
指数衰减中,每增加一个网格长度的距离,影响力减少一定倍数.其影响力大小与距离的关系为
| $ I_{p, i}=\left\{\begin{array}{l}{I_{i} \gamma^{d_{i, p}}, \quad d_{i, p} \leqslant D} \\ {0, \quad d_{i, p}>D}\end{array}\right. $ | (2) |
其中γ为衰减比.
2.2 传播方式传播方式是指初始传播点和传播目标点间距离的计算方式,通常有直接使用欧式距离作为衰减依据、使用两点间路径的长度作为衰减依据、临近传播的3种方法.
1) 基于欧式距离的传播
使用欧式距离作为传播依据的影响力地图中,di, p计算方式为
| $ d_{i, p}=d_{\mathrm{E}(i, p)} $ | (3) |
其中dE(i, p)为p和i之间的欧几里得距离.
这种传播方式仅计算两点之间连线的距离,若p与i之间有障碍物时,这种传播方式将穿过障碍传播影响力,这显然是不准确的.
2) 基于路径的传播
路径传播使用两点间路径长度来确定距离:
| $ d_{i, p}=d_{\mathrm{path}(i, p)} $ | (4) |
其中dpath(i, p)为p和i之间的路径长度.
路径的计算过程中会考虑障碍因素,故这种方法在有障碍的环境中使用时准确度会好于上面的方法,但其缺陷是需要计算大量的路径.而寻路算法的复杂度通常是较高的,这样的复杂度对游戏AI开发通常是不可接受的.通常的做法是预先计算好影响力地图上任意两点间的路径长度,在影响力地图传播过程中直接通过查询得到路径长度[3].这要求在游戏过程中地形不会发生变化.
3) 临近传播
临近传播不再显式地计算路径长度,其基本思想是将初始传播点的影响力使用线性衰减或指数衰减的方式传播到临近的网格(对于方格地图,可以向4个或8个方向传播;对于六边形地图,向周围的6个方向传播),若这些网格中的一些影响力有更新,则从这些网格再次使用同样的方法向周围传播.整个传播过程类似于漫水填充算法(洪水填充算法,flood-fill).
临近传播无法使用距离作为传播停止条件,因此采用影响力绝对值大小作为停止传播的判断条件.停止传播的阈值计算方法为
对于线性衰减:
| $ t=\left|I_{i}-\beta D\right| $ | (5) |
对于指数衰减:
| $ t=\left|I_{i} \gamma^{D}\right| $ | (6) |
当|Ip, i| < t时停止传播.
由于临近传播方法不依赖预先计算的路径长度,所有的影响力传播过程可实时计算,所以可以在动态地图的游戏中方便地使用.
2.3 整体影响力地图的计算通过上述计算过程可以得到单个游戏对象对某点的影响力.某点的最终影响力信息为各个游戏对象产生影的响力之和,某一点的最终影响力计算方式为
| $ I(p)=\sum\limits_{i \in U} I_{p, i} $ | (7) |
其中U为游戏中所有游戏对象的集合.
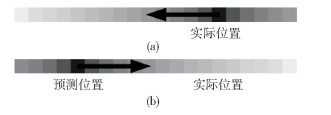
3 基于距离调整的动态影响力地图模型 3.1 研究动机传统的影响力地图算法缺乏对游戏对象运动信息的反馈.而在大部分游戏中运动的游戏对象对其运动方向和其他方向的影响是不相同的.将这些动态信息通过计算编码到影响力地图中可以使游戏AI主体更好地理解游戏当前状态.在Game Programming Gems 2中的影响力地图部分[3]提到了一种非常简单的考虑游戏对象运动信息的方法.该方法使用航位推测法(DR,dead reckoning)[7]预测其未来某一时刻的位置,将该游戏对象的初始影响力放置在该位置,并从该位置进行传播.但是这种计算方法对于从产生影响的游戏对象的实际位置到预测位置之间的一段距离,计算得到的影响力地图不仅是数值不是十分准确,而且趋势完全错误,如图 1所示.
|
图 1 位置偏移的方法导致局部影响力趋势错误 |
设计了一种基于距离调整的动态影响力地图模型,在影响力传播的过程中,在不同的方向上传播时的影响力大小不同.不同于文献[3]中对产生影响的游戏对象的位置进行偏移,提出的模型对产生影响的游戏对象到需要计算影响力的点的距离进行调整,使用调整后的距离计算影响力,从而达到对不同方向等距离的点传播不同影响力的效果.这种方法可以很方便地与上述指数衰减、线性衰减和欧式距离传播、路径传播、临近传播方法相结合.
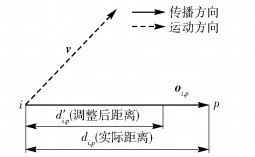
将从游戏对象到地图上要计算影响力的点的向量定义为传播方向向量,以运动方向向量和传播方向向量的余弦值表示2个向量方向的相似度.为了表达不同方向上传播的影响力大小不同,根据2个向量的相似度对距离做出调整,如图 2所示.
|
图 2 距离调整 |
调整距离的计算方法为
| $ d_{i, p}^{\prime}=\frac{d_{i, p}}{1+\cos \left(\boldsymbol{o}_{i p}, \boldsymbol{v}\right) \alpha} $ | (8) |
其中:p为需要计算影响力的点;i为产生影响的点(即产生影响的游戏对象的位置);di, p为两点间的实际距离;d′i, p表示调整后的距离;oip为从i出发,去往p的传播方向向量;v为当前游戏对象的运动方向向量;α为距离变换系数,0 < α < 1,通常与游戏对象的运动速度相关,具体值的设定与游戏环境因素相关,可由实验来确定. α值越大,表示在运动方向上获得的影响力相对越大.
由式(8)知,在运动方向与传播方向相同时,2个向量的余弦值最大,调整后的距离最小,影响力将变大;在运动方向与传播方向相反时,调整后距离最大,调整后的影响力变小;在两方向相互垂直时,d′i, p=di, p.
在式(8)中,di, p和oip的具体取值与采用的传播方式有关.
在调整后距离的基础上,根据2.1中的衰减公式,即可计算影响力地图上任意点的影响.
3.3 在欧式距离传播方式下的具体细节使用欧式距离传播的影响力地图中,di, p、oip的计算方式为
| $ d_{i, p}=d_{\mathrm{E}(i, p)} $ | (9) |
| $ \boldsymbol{o}_{i p}=\overrightarrow{i p} $ | (10) |
其中:dE(i, p)为传播起点i和传播终点p之间的欧氏距离,
在使用路径传播的影响力地图中,di, p、oip的计算方式为
| $ d_{i, p}=d_{\text {path }(i, p)} $ | (11) |
| $ \boldsymbol{o}_{i p}=\overrightarrow{i N_{\mathrm{path}(i, p)}} $ | (12) |
其中:dpath(i, p)为传播起点i和传播终点p之间的路径长度,Npath(i, p)为点i到点p的路径上的下一个网格,
临近传播方法的思路是将某点的影响力先向其相邻的网格传播,如果这些网格数据有更新,在这些网格再次进行临近传播,直到达到传播停止的条件.
临近传播不会显式地计算两点间的路径,因此设计了传播矩阵,在该矩阵上表现传播方向.传播矩阵随着传播过程在影响力地图上移动,能够在整个影响力地图上大致反应运动信息.
以下为在四边形网格地图情况下,采用8个方向的漫水填充算法.
首先定义一个大小为3×3的传播矩阵K,对于线性衰减,在该矩阵上以中心点作为出发点,使用欧式距离的传播方法计算衰减量:
| $ k_{i, j}=\beta \frac{d_{\mathrm{E}(i, p)}}{1+\cos (\overrightarrow{i p}, \boldsymbol{v}) \alpha} $ | (13) |
对于指数衰减,在该矩阵上以中心点作为出发点,使用欧式距离的传播方法计算衰减比:
| $ k_{i, j}=\gamma\left(\frac{d_{\mathrm{E}(i, p)}}{1+\cos (\overrightarrow{i p}, \boldsymbol{v}) \alpha}\right) $ | (14) |
其中β和γ分别表示线性衰减中的衰减速度和指数衰减中的衰减比.
使用式(5)或(6)计算停止传播的阈值t,之后,使用下面的算法进行影响力的传播.
算法 基于距离调整的临近传播算法
将游戏对象i的初始影响力Ii放置于游戏对象所在方格(x, y),即I(x, y), i=Ii.
其他方格赋值为0.即I(u, v), i=0 (u≠x, v≠y).
将(x, y)放置到待传播队列q中
while q不为空
从q取出一个待传播起点(x, y)
将传播矩阵中心放置在传播起点(x, y)
if使用线性衰减then
I′(x-u+1, y-v+1), i=Ix, y-ku, v (0≤u, v≤2)
else if使用指数衰减then
I′(x-u+1, y-v+1), i=Ix, yku, v (0≤u, v≤2
end
对于传播矩阵上所有点(i, j), (0≤u, v≤2)
If |I′(x-u+1, y-v+1), i|>|I(x-u+1, y-v+1), i| and |I′(x-u+1, y-v+1), i|>t
and (x-u+1, y-v+1)可通行then
I(x-u+1, y-v+1), i=I′(x-u+1, y-v+1), i
将(x-u+1, y-v+1)加入待传播队列q
end
end
end
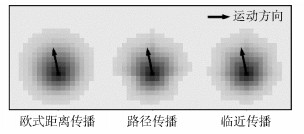
3.6 传播效果分析考虑动态信息的目的是在不同方向上传播不同大小的影响力.通过热力图可以直观地分析不同方向上的影响力大小关系.下面的热力图显示了在使用指数衰减且使用距离调整方法的情况下,3种传播方式产生的影响效果.
如图 3所示,3种传播方式产生的影响力地图均在运动方向附近产生了相对较大的影响力,且传播距离较远;与运动方向偏差越大的方向,影响力较小,传播距离较近.这表明,3种传播方式下,使用距离调整的影响力地图模型均可近似表示出游戏对象不同方向上产生影响力的差异.
|
图 3 使用3种传播方式的传播示意图 |
对于上述基于距离调整的动态影响力地图模型,设计了在吃豆人女士(Ms. Pac-Man)游戏中的实验.吃豆人女士是1980年发布的吃豆人(Pac-Man)的继承者.吃豆人女士游戏中需要考虑的环境因素很多,包括豆子、能量药丸、恶魔、可以被吃掉的恶魔.但其决策空间非常小,只需要确定自身的移动方向即可(至多4个方向),因此非常适合作为影响力地图的实验场景.同时,吃豆人女士游戏也是游戏AI研究领域的重要平台,吃豆人女士竞赛(CIG 2007—2011)和吃豆人女士Vs.恶魔团队竞赛(CIG 2016—2018)都使用吃豆人女士游戏作为竞赛和研究平台.
4.2 模型与吃豆人女士游戏的结合Wirth等[4-5]已经提出了一些用于吃豆人女士的影响力地图模型.综合这2篇文章,设计了如下影响力地图模型.
| $ \begin{aligned} I(s) ~~~=\sum\limits_{p \in U_{{\rm p}}} I_{\mathrm{p}}(s, p)+\sum\limits_{P \in U_{\mathrm{P}}} I_{\mathrm{P}}(s, P)+\\ ~~~ \sum\limits_{g \in U_{\mathrm{g}}} I_{\mathrm{g}}(s, g)+\sum\limits_{G \in U_{\mathrm{G}}} I_{\mathrm{G}}(s, G) \end{aligned} $ | (15) |
| $ I_{\mathrm{p}}(s, p)=\left\{\begin{array}{ll}{\tilde{I}_{\mathrm{p}} \gamma^{d_{s, p}}, } ~~~ {d_{p, s} \leqslant D_{\mathrm{p}}} \\ {0, } ~~~ {d_{p, s}>D_{\mathrm{p}}}\end{array}\right. $ | (16) |
| $ I_{\mathrm{P}}(s, P)=\left\{\begin{array}{ll}{\tilde{I}_{\mathrm{P}} \gamma^{d_{P, s}}, } ~~~ {d_{P, s} \leqslant D_{\mathrm{p}}} \\ {0, } ~~~ {d_{P, s}>D_{\mathrm{p}}}\end{array}\right. $ | (17) |
| $ I_{\mathrm{g}}(s, g)=\left\{\begin{array}{ll}{\tilde{I}_{\mathrm{g}} \gamma^{d_{g, s}}, } ~~~ {d_{g, s} \leqslant D_{\mathrm{g}}} \\ {0, } ~~~ {d_{g, s}>D_{\mathrm{g}}}\end{array}\right. $ | (18) |
| $ I_{\mathrm{G}}(s, G)=\left\{\begin{array}{ll}{\tilde{I}_{\mathrm{G}} \gamma^{d_{G, s}}, } ~~~ {d_{G, s} \leqslant D_{\mathrm{g}}} \\ {0, } ~~~ {d_{G, s}>D_{\mathrm{g}}}\end{array}\right. $ | (19) |
其中参数含义如表 1所示.
|
|
表 1 参数含义 |
在影响力地图中,通常可以将网格宽和高设置为刚好容纳10~20个标准游戏对象,然后通过实验进行调整[3].但对于吃豆人女士这样的小型地图来说,10~20个游戏对象的网格过大,参考文献[5]中的设计方案,本实验模型采用宽28高31的网格作为影响力地图,所有坐标采用该网格中的坐标.
本实验中的吃豆人女士控制器在影响力地图的基础上进行决策.控制器观察吃豆人女士当前位置所有相邻的方格(至多4个方向),找出影响力最大的一个方向,并向该方向移动.
4.3 实验方案针对影响力地图的3种传播方式,分别设计了3组对照实验.在每组对照中,采用了不考虑运动信息、位置偏移、距离调整的方法进行实验,通过比较平均得分的方式检验性能.
对于位置偏移的模型,将恶魔的位置向运动方向偏移O个方格(O的取值如表 2所示);对于距离调整的模型,使用距离调整算法得到的调整后距离作为dp, s的值.
|
|
表 2 参数范围 |
在实际的影响力地图开发中,参数设定通常是依据经验来进行的,之后通过实验验证和调整.为了方便比较不同模型的性能,设计了参数搜索的实验,使用每个模型的最优参数进行对比.
对于每个模型的每组参数,运行游戏50次,并计算平均得分.
4.4 实验结果1) 游戏得分
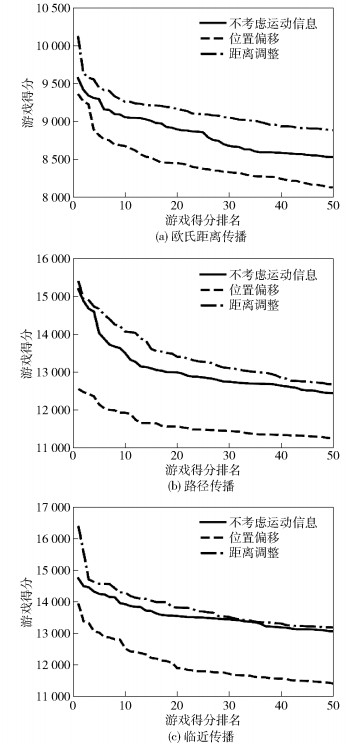
取每个模型中最优的50组数据,并按照从高到底的顺序排列,实验结果如图 4所示.
|
图 4 实验结果 |
在3种传播方式下,基于距离调整的影响力地图模型均有较大优势,可达到的最高分数相较于不考虑动态信息的模型分别提高了5.83%、1.46%、11.35%.可见,采用该算法,将速度和方向信息融合到影响力地图中后,有效地提高了游戏AI主体的决策能力.同时,实验结果显示,位置偏移的方法存在一定缺陷,有造成AI主体决策错误,降低性能的可能性.
2) 算法运行时间分析
在改进后的模型中,传播算法的时间复杂度不变,因此不会显著降低传播算法的效率.
在相同场景下使用不同的模型,在整个游戏场景内多次进行影响力地图的计算,统计平均的计算时间,如表 3所示.
|
|
表 3 算法运行时间 |
可见,位置偏移方法和距离调整方法相对于不考虑运动信息的方法,相同条件下的整个影响图计算时间均有所增加.对于欧式距离方法,增加了9.38%,在实际使用过程中,需要权衡性能与计算代价.对于路径传播和临近传播,增幅仅为0.8%和0.1%,相对于带来的性能提升,增加的运行时间较少.
5 结束语提出了一种基于距离调整的动态影响力地图模型及相应的计算方法,根据运动方向与传播方向的相似度,调整两点间距离,在游戏对象的不同方向,产生不同的影响力,从而在影响力地图上反映出游戏场景中的动态信息,弥补了传统影响力地图中位置预测方法的不足,提高了对游戏环境描述的准确性,为决策系统提供了更好的支持.同时在吃豆人女士游戏中进行了实验验证,实验结果表明,该方法可以有效提高影响力地图的准确性,在游戏中获得更高的分数.
| [1] |
Zobrist A L. A model of visual organization for the game of GO[C]//Proceedings of AFIPS. New York: ACM, 1969: 103-112.
|
| [2] |
Miles C, Louis S J. Co-evolving real-time strategy game playing influence map trees with genetic algorithms[C/OL]//Proceedings of the International Congress on Evolutionary Computation. Portland: IEEE Press, 2006[2018-06-21]. https://www.cse.unr.edu/~sushil/pubs/newestPapers/2006/cec2006/cec2006.pdf.
|
| [3] |
DeLoura M. Game programming gems 2[M]. Hingham: Charles River Media, 2001: 287-297.
|
| [4] |
Wirth N, Gallagher M. An influence map model for playing Ms. Pac-Man[C]//2008 IEEE Symposium on Computational Intelligence and Games. Perth: IEEE Press, 2008: 228-233.
|
| [5] |
Svensson J, Johansson S J. Influence map-based controllers for Ms. PacMan and the ghosts[C]//2012 IEEE Conference on Computational Intelligence and Games. Granada: IEEE Press, 2012: 257-264.
|
| [6] |
Koren Y, Borenstein J. Potential field methods and their inherent limitations for mobile robot navigation[C]//Proceedings of 1991 IEEE International Conference on Robotics and Automation. Sacramento: IEEE Press, 1991: 1398-1404.
|
| [7] |
Lin K C. Dead reckoning and distributed interactive simulation[C/OL]//Distributed Interactive Simulation Systems for Simulation and Training in the Aerospace Environment: a Critical Review. Bellingham: SPIE, 1995[2018-06-21]. https://doi.org/10.1117/12.204227.
|


