近年来，毫米波大规模多输入多输出(Massive-MIMO, massive multiple input multiple output)技术引起了广泛的关注和研究.这主要是因为毫米波通信具有丰富的频谱资源，结合Massive-MIMO的混合预编码技术能够获取更高的波束增益，以此可弥补毫米波通信高损耗的传播缺陷^[1-3].但与此同时，硬件规模和编解码复杂度日益增长，需要寻找新的混合预编码方案以降低系统复杂度.

MIMO复用系统通常采用奇异值分解(SVD，singular value decomposition)方式得到多个独立的正交空间子信道以获得较大的吞吐量.然而，由于此方式下各子信道增益差异很大^[4]，需要使用不同的编解码和调制解调方式以满足误码率(BER，bit error rate)的要求，使得系统复杂度很高.为此，Jiang等^[5]提出了一种基于几何均值分解(GMD，geometric mean decomposition)方案.该方案将正交频分复用下的瑞利衰落信道分解为多个信道增益相等的并行子信道，从而避免了复杂的比特分配和功率加载过程，并降低了系统的编解码的难度，从而整体上降低了系统复杂度.在此基础上，为了获取频效性能最优的混合预编码方案，El Ayach等^[6]通过将频效优化问题转化为稀疏近似问题，并通过正交匹配追踪(OMP，orthogonal matching pursuit)^[7]算法优化单用户MIMO系统的下行频效. Kaushik等^[8]在研究单用户MIMO系统频效时，设计混合预编码方案，并提出最优化系统频效的算法，但其只考虑了算法的优化问题，在系统编解码复杂度方面没有进行深入研究. Ahrens等^[9]在研究MIMO信道对角化的基础上，通过GMD方法有效补偿SVD时加权子信道的增益差异缺陷. Chen等^[10]在单用户MIMO中讨论了反馈速率较小的前提下，差分GMD预编码器对于系统频效的影响，但其系统频效与基站天线数、信噪比的关系仍然不明确，难以在实际通信环境中推广.

基于毫米波Massive-MIMO下行链路系统频效的研究现状，将GMD的信道处理方式应用于毫米波Saleh-Valenzuela(S-V)信道处理中，相比于基于SVD信道处理方式，能够有效降低系统复杂度，并在此基础上，针对移动通信下行链路单用户通信场景，提出一种可适用于毫米波Massive-MIMO系统的基于GMD混合预编码方案，该方案可在降低系统复杂度的前提下获得最优的系统频效.

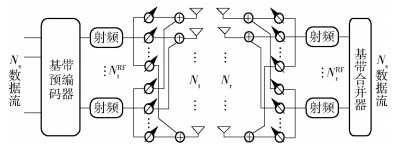
1 系统模型 1.1 混合预编码模型

提出的毫米波Massive-MIMO系统模型如图 1所示.为了简化分析，系统仅考虑单小区、单个用户的下行传输场景，基站配置N_t根天线和N_t^RF个射频链，传输数据包含N_s个数据流，满足N_s≤N_t^RF≤N_t.用户接收机配置N_r根天线和N_r^RF个射频链，满足N_s≤N_r^RF≤N_r.

混合预编码在基站端完成，由数字预编码P_D∈C^N_tRF×N_s和模拟预编码P_A∈C^N_t×N_tRF构成，相应的基站预编码为P=P_AP_D.假设基站发送信号矢量为s，则混合预编码后的信号为

$ \boldsymbol{x}=\boldsymbol{P s}=\boldsymbol{P}_{\mathrm{A}} \boldsymbol{P}_{\mathrm{D}} \boldsymbol{s} $

(1)

其中P为基站发射功率，满足tr{PP^H}≤N_s.相应地，用户接收的信号矢量为

$ \boldsymbol{y}=\sqrt{\rho} \boldsymbol{H} \boldsymbol{P}_{\mathrm{A}} \boldsymbol{P}_{\mathrm{D}} \boldsymbol{s}+\boldsymbol{n} $

(2)

其中：(·)^H为复共轭转置运算；ρ为平均接收功率；H∈C^N_r×N_t为毫米波信道传输矩阵；n∈C^N_r×1为噪声向量，服从复高斯分布，即CN(0, σ²I_Nr)，其中σ²为噪声方差，I_Nr为N_r×N_r维单位阵.模拟预编码P_A通过移相器网络实现，且满足恒模限制，即|{P_A}_{i, j}|=$ \sqrt{N_{\mathrm{t}}}$，式中{·}_{i, j}为矩阵的第i行j列上的元素，|·|为取复数的模值.

1.2 信道模型

毫米波信道采用S-V模型^[11]，信道转移矩阵H可表示为

$ \mathit{\boldsymbol{H}} = \sqrt {\frac{{{N_{\rm{t}}}{N_{\rm{r}}}}}{L}} \sum\limits_i^L {{\beta _i}} {\alpha _r}\left( {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_i^{\rm{r}}} \right){\alpha _{\rm{i}}}\left( {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_i^{\rm{t}}} \right) $

(3)

其中：L为(可分辨)信道路径数，β_i为第i条路径的复增益，Φ_i^r和Φ_i^t分别为第i条路径的到达角(AoAs，angles of arrival)和离开角(AoDs，angles of departure)，α_r(Φ_i^r)和α_t(Φ_i^t)为用户接收机对应于Φ_i^r和基站发射机对应于Φ_i^t的天线阵列响应矢量.对于包含N个元素的简单均匀线性阵列(ULA，uniform linear array)，阵列响应矢量为

$ {\partial _{{\rm{ULA}}}}(\mathit{\Phi }) = \sqrt {\frac{1}{N}} {\left[ {1, {{\rm{e}}^{{\rm{j}}kd\sin (\mathit{\Phi })}}, \cdots , {{\rm{e}}^{{\rm{j}}(N - 1)kd\sin (\mathit{\Phi })}}} \right]^{\rm{T}}} $

(4)

其中：k=2π/λ，λ为波长；d为天线间隔距离.由于毫米波传播中有限的空间散射性，相应的毫米波MIMO信道矩阵是低秩矩阵，所以可以通过有限的射频链获得接近最优的系统频效^[12].

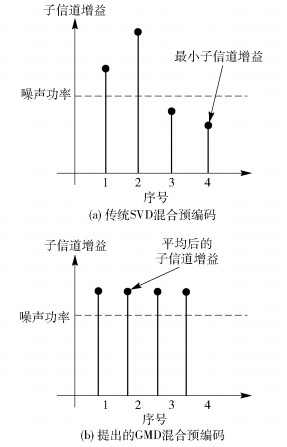
2 基于GMD的混合预编码方案 2.1 问题描述

毫米波在传播中有限的空间散射，使得信道矩阵H的奇异值变化很大^[4]，这导致了不同子信道在功率分配后的信噪比(SNR，signal to noise ratio)差异较大，如图 2(a)所示.在相同的调制/解调方式下，所有子信道的误码率由最低SNR的子信道决定.为了保证所有子信道保持相似的误码率，基于SVD的预编码方案需要对各子信道进行谨慎的比特分配，这将使系统编/解码环节复杂度大大增加^[13].然而，信道H采用GMD方法能有效地均衡各子信道的SNR^[9-10]，如图 2(b)所示，避免了复杂的子信道比特分配和功率加载过程，并降低系统编解码复杂度，从而整体上降低系统复杂度.基于此，将设计基于GMD混合预编码优化矩阵，以图在较低的编解码和调制解调复杂度下，得到系统频效的优化值.由式(2)得系统频效为^[14]

$ R=\operatorname{lb}\left(\operatorname{det}\left(\boldsymbol{I}+\frac{\rho}{N_{{\rm s}} \sigma_{n}^{2}} \boldsymbol{H} \boldsymbol{P}_{\rm{A}} \boldsymbol{P}_{\mathrm{D}} \boldsymbol{P}_{\mathrm{D}}^{\mathrm{H}} \boldsymbol{P}_{{\rm A}}^{\mathrm{H}}\boldsymbol{H}^{{\rm H}}\right)\right) $

(5)

为了使R最优，必须对多个参数进行优化.在毫米波预编码情况下，P_A和P_D在非凸约束的条件下难以得到准确解.为了简化预编码设计，采用解耦方式设计基站和用户端的预编码及解码矩阵^[6].

2.2 基于GMD的系统频效优化函数

由文献[5]可知，对于任意的具有秩为N_s、奇异值为σ₁≥σ₂≥… ≥σ_Ns的复信道矩阵H可表示为

$ \boldsymbol{H}=\boldsymbol{G}_{\mathrm{GMD}} \boldsymbol{R}_{\mathrm{GMD}} \boldsymbol{Q}_{\mathrm{GMD}}^{\mathrm{H}}=\left[\boldsymbol{G}_{1} \boldsymbol{G}_{2}\right]\left[\begin{array}{cc}{\boldsymbol{R}_{1}} & {*} \\ {0} & {\boldsymbol{R}_{2}}\end{array}\right]\left[\begin{array}{l}{\boldsymbol{Q}_{1}^{\mathrm{H}}} \\ {\boldsymbol{Q}_{2}^{\mathrm{H}}}\end{array}\right] $

(6)

其中：G_GMD=[G₁ G₂]∈C^N_r×N_r，G₁∈C^N_r×N_s为包含酉矩阵G_GMD左起N_s列向量的半正定矩阵；Q_GMD=$ \left[\begin{array}{l}{\boldsymbol{Q}_{1}^{\mathrm{H}}} \\ {\boldsymbol{Q}_{2}^{\mathrm{H}}}\end{array}\right] \in C^{N_{{\rm t}} \times N_{1}}$为酉矩阵，Q₁∈C^N_t×N_s为包含酉矩阵Q_GMD左起N_s列向量的半正定矩阵；R_GMD=$ \left[\begin{array}{cc}{\boldsymbol{R}_{1}} & {*} \\ {0} & {\boldsymbol{R}_{2}}\end{array}\right] \in C^{N_{\mathrm{r}} \times N_{\mathrm{t}}}$为含有矩阵H奇异值的对角矩阵.其中，R₁∈C^N_s×N_s是一个具有相同对角元素的上三角矩阵，它的对角元素包含矩阵H的前N_s个奇异值的几何均值.即对于∀_i，有r_{i, i}=(σ₁，σ₂，…，σ_Ns)^1/N_s=r成立，r_{i, i}等效为GMD处理后的并行子信道增益，σ_{1, 2, …, Ns}为H的奇异值. R₂∈C^{(N_r-N_s)×(N_t-N_s)}为三角矩阵，其对角元素为矩阵H自N_s之后的奇异值，*对应的矩阵元素为任意值.由于仅有N_s个传输数据流，在此只考虑前N_s个奇异值的几何均值.

通过式(6)将对信道矩阵H进行GMD处理，则处理后的系统频效函数可表示为

$ R=\operatorname{lb}\left(\operatorname{det}\left(\boldsymbol{I}+\frac{\boldsymbol{\rho}}{N_{\mathrm{s}} \boldsymbol{\sigma}_{n}^{2}} \boldsymbol{R}_{\mathrm{GMD}}^{2} \boldsymbol{Q}_{\mathrm{GMD}}^{\mathrm{H}} \boldsymbol{P}_{\mathrm{A}} \boldsymbol{P}_{\mathrm{D}} \boldsymbol{P}_{\mathrm{D}}^{\mathrm{H}} \boldsymbol{P}_{\mathrm{A}}^{\mathrm{H}} \boldsymbol{Q}_{\mathrm{GMD}}\right)\right) $

(7)

假设P=P_AP_D非常接近最优酉矩阵Q_res=Q₁，则可得到以下2个近似结论^[6]：

1) 矩阵I_Ns-Q₁^HP_AP_DP_D^HP_A^HQ₁的特征值较小，因此在毫米波预编码中可等价表示为Q₁^HP_AP_D≈I_Ns；

2) 更进一步，由于Q₂^HP_AP_D的奇异值较小，可等效为Q₁^HP_AP_D≈0，因此可得到如下变换式：

$ \begin{array}{c}{\boldsymbol{Q}_{\mathrm{GMD}}^{\mathrm{H}} \boldsymbol{P}_{\mathrm{A}} \boldsymbol{P}_{\mathrm{D}}\boldsymbol{P}_{\mathrm{D}}^{\mathrm{H}} \boldsymbol{P}_{\mathrm{A}}^{\mathrm{H}} \boldsymbol{Q}_{\mathrm{GMD}}=} \\ \left[ \begin{array}{c}{\boldsymbol{Q}_{1}^{\mathrm{H}} \boldsymbol{P}_{\mathrm{A}} \boldsymbol{P}_{\mathrm{D}} \boldsymbol{P}_{\mathrm{D}}^{\mathrm{H}} \boldsymbol{P}_{\mathrm{A}}^{\mathrm{H}}\boldsymbol{Q}_{1}} & {\boldsymbol{Q}_{1}^{\mathrm{H}} \boldsymbol{P}_{\mathrm{A}} \boldsymbol{P}_{\mathrm{D}}\boldsymbol{P}_{\mathrm{D}}^{\mathrm{H}} \boldsymbol{P}_{\mathrm{A}}^{\mathrm{H}} \boldsymbol{Q}_{2}} \\ {\boldsymbol{Q}_{2}^{\mathrm{H}} \boldsymbol{P}_{\mathrm{A}} \boldsymbol{P}_{\mathrm{D}} \boldsymbol{P}_{\mathrm{D}}^{\mathrm{H}} \boldsymbol{P}_{\mathrm{A}}^{\mathrm{H}}\boldsymbol{Q}_{1}} & {\boldsymbol{Q}_{2}^{\mathrm{H}} \boldsymbol{P}_{\mathrm{A}} \boldsymbol{P}_{\mathrm{D}}\boldsymbol{P}_{\mathrm{D}}^{\mathrm{H}} \boldsymbol{P}_{\mathrm{A}}^{\mathrm{H}}\boldsymbol{Q}_{2}}\end{array} \right]= \\ {\left[\begin{array}{cc}{\boldsymbol{Q}_{11}} & {\boldsymbol{Q}_{12}} \\ {\boldsymbol{Q}_{21}} &{\boldsymbol{Q}_{22}}\end{array}\right]}\end{array} $

(8)

将式(8)代入式(7)得

$ \begin{array}{c} R=\mathrm{lb}\left(\operatorname{det}\left(\boldsymbol{I}+\frac{\rho}{N_{{\rm s}} \sigma_{n}^{2}}\left[\begin{array}{cc}{\boldsymbol{R}_{1}^{2}} & {*} \\ {0} & {\boldsymbol{R}_{2}^{2}}\end{array}\right]\left[\begin{array}{ll}{\boldsymbol{Q}_{11}} & {\boldsymbol{Q}_{12}} \\ {\boldsymbol{Q}_{21}} & {\boldsymbol{Q}_{22}}\end{array}\right]\right)\right) \approx\\ \operatorname{lb}\left(\operatorname{det}\left(\boldsymbol{I}_{N_{{\rm s}}}+\frac{\rho}{N_{{\rm s}} \sigma_{n}^{2}} \boldsymbol{R}_{1}^{2} \boldsymbol{Q}_{1}^{\mathrm{H}} \boldsymbol{P}_{\mathrm{A}} \boldsymbol{P}_{\mathrm{D}} \boldsymbol{P}_{\mathrm{D}}^{\mathrm{H}} \boldsymbol{P}_{\Lambda}^{\mathrm{H}} \boldsymbol{Q}_{1}\right)\right)=\\ \operatorname{lb}\left(\left|\boldsymbol{I}_{N_{\mathrm{{\rm s}}}}+\frac{\rho}{N_{\mathrm{s}} \sigma_{n}^{2}} \boldsymbol{R}_{1}^{2}\right|\right)-\left(N_{\mathrm{s}}-\left\|\boldsymbol{Q}_{1}^{\mathrm{H}} \boldsymbol{P}_{\mathrm{A}} \boldsymbol{P}_{\mathrm{D}}\right\|_{\mathrm{F}}^{2}\right) \end{array} $

(9)

式(9)的第1项可以通过令Q_res=R₁实现，第2项实际上是格拉斯曼流形(Grassmann manifold)上两点Q_res=R₁和(P_AP_D)之间的平方和弦距离，可用欧式距离‖Q_res-Q_AQ_D‖_F代替.因此，最大化系统频效的问题可转换为最小化‖Q_res-Q_AQ_D‖_F问题.

假设Q_res为基于GMD的最优预编码，Q_A、Q_D分别为相应的模拟预编码和数字预编码，则转化后的优化目标函数为

$ \begin{aligned}\left(\boldsymbol{Q}_{\mathrm{A}}^{\mathrm{opt}}, \boldsymbol{G}_{\mathrm{D}}^{\mathrm{opt}}\right) &=\underset{\boldsymbol{Q}_{\mathrm{A}}, \boldsymbol{Q}_{\mathrm{D}}}{\arg \min }\left\|\boldsymbol{Q}_{\mathrm{res}}-\boldsymbol{Q}_{\mathrm{A}} \boldsymbol{Q}_{\mathrm{D}}\right\|_{\mathrm{F}} \\ \text { s.t. } | &\left\{\boldsymbol{Q}_{\mathrm{A}}\right\}_{i, j} |=1 / \sqrt{N_{\mathrm{t}}}, \\ & \operatorname{tr}\left(\boldsymbol{Q}_{\mathrm{A}} \boldsymbol{Q}_{\mathrm{D}} \boldsymbol{Q}_{\mathrm{D}}^{\mathrm{H}} \boldsymbol{Q}_{\mathrm{A}}^{\mathrm{H}}\right) \leqslant N_{\mathrm{s}} \end{aligned} $

(10)

2.3 转换优化目标函数

为了降低GMD变换的复杂性并得到式(10)的优化解，可以通过引理1将优化问题加以转化.

引理1  假设信道矩阵H的SVD为

$ \boldsymbol{H}=\boldsymbol{U} \mathit{\boldsymbol{ \boldsymbol{\varSigma} }} \boldsymbol{V}^{\mathrm{H}}=\left[\boldsymbol{U}_{1} \boldsymbol{U}_{2}\right]\left[\begin{array}{cc}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{1}} & {0} \\ {0} & {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{2}}\end{array}\right]\left[\begin{array}{c}{\boldsymbol{V}_{1}^{\mathrm{H}}} \\ {\boldsymbol{V}_{2}^{\mathrm{H}}}\end{array}\right] $

(11)

信道矩阵的奇异值按降序排列，则存在酉矩阵S_R∈C^N_s×N_s, S_L∈C^N_s×N_s使得Q₁=V₁S_R; G₁=U₁S_L; R₁=S_L^TΣ₁S_R.

证明  计算信道矩阵的几何均值r=(σ₁，σ₂，…，σ_Ns)^1/N_s，定义辅助矩阵：

$ \boldsymbol{R}_{1}:=\left\{\boldsymbol{M}^{(i)}\right\}^{\mathrm{H}} \boldsymbol{R}_{1} \boldsymbol{M}^{(i)}, \boldsymbol{Q}_{1}:=\boldsymbol{Q}, \boldsymbol{M}^{(i)}, \boldsymbol{G}_{1}:=\boldsymbol{G}_{1} \boldsymbol{M}^{(i)} $

(12)

其中：“:=”表示“定义为”，M⁽ⁱ⁾为对应的置换矩阵.令R₁=Σ₁，Q₁=V₁，G₁=U₁，并定义2个从I_Ns中替换含有4个元素{N_L⁽ⁱ⁾}_{i, i}，{N_L⁽ⁱ⁾}_{i+1, i}，{N_L⁽ⁱ⁾}_{i, i+1}，{N_L⁽ⁱ⁾}_{i+1, i+1}的子矩阵生成的矩阵N_L⁽ⁱ⁾和N_R⁽ⁱ⁾，其中的4个元素有以下二维矩阵的形式：

$ \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{\mathrm{L}}^{(i)}=\frac{1}{r}\left[\begin{array}{cc}{c r_{i, i}} & {s r_{i+1, i+1}} \\ {-s r_{i+1, i+1}} & {c r_{i, i}}\end{array}\right], \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{\mathrm{R}}^{(i)}=\left[\begin{array}{cc}{c} & {-s} \\ {s} & {c}\end{array}\right] $

(13)

若r_{i, i}=r_{i+1, i+1}=r，取c=1, s=0，若r_{i, i}≠r_{i+1, i+1}，取

$ c=\sqrt{\frac{\bar{r}^{2}-r_{i+1, i+1}^{2}}{r_{i, i}^{2}-r_{i+1, i+1}^{2}}}, s=\sqrt{1-c^{2}} $

(14)

更新R₁、Q₁和G₁，则

$ \boldsymbol{R}_{1}:=\boldsymbol{N}_{\mathrm{L}}^{(i)} \boldsymbol{R}_{1} \boldsymbol{N}_{\mathrm{R}}^{(i)}, \boldsymbol{Q}_{1}:=\boldsymbol{Q}_{1}\left\{\boldsymbol{N}_{\mathrm{L}}^{(i)}\right\}^{\mathrm{T}}, \boldsymbol{G}_{1}:=\boldsymbol{G}_{1} \boldsymbol{N}_{\mathrm{R}}^{(i)} $

(15)

进一步得

$ \boldsymbol{R}_{1}^{i+1}=\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{\mathrm{L}}^{(i)}\left[\begin{array}{cc}{r_{i, i}} & {0} \\ {0} & {r_{i+1, i+1}}\end{array}\right] \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_{R}^{(i)}=\left[\begin{array}{cc}{\bar{r}} & {*} \\ {0} & {\frac{r_{i, i} r_{i+1, i+1}}{\bar{r}}}\end{array}\right] $

(16)

这表明通过N_L⁽ⁱ⁾R₁N_R⁽ⁱ⁾，就可以使r_{i, i}=r，并且保持其他元素不变.依次将R_i替换R₁代入计算，其中1≤i≤N_s-1.

式(15)表明M⁽ⁱ⁾、N_L⁽ⁱ⁾和N_R⁽ⁱ⁾均为酉矩阵，且式(16)表明，通过GMD变换只改变了对角元素的取值，其他元素保持不变.因此可以构造矩阵S_L=M⁽¹⁾N_R⁽¹⁾M⁽²⁾N_R⁽²⁾…M^(N_s)N_R^(N_s)和S_R=M⁽¹⁾{N_L⁽¹⁾}^TM⁽²⁾{N_L⁽²⁾}^T…M^(N_s){N_L^(N_s)}^T，代入式(15)，得R₁=S_L^TΣ₁S_R.类似地，有Q₁=V₁S_R; G₁=U₁S_L.引理1得证.

根据引理1，式(10)等号右边可以改写为

$ \begin{array}{c}\left\|\boldsymbol{Q}_{\mathrm{res}}-\boldsymbol{Q}_{\mathrm{A}} \boldsymbol{Q}_{\mathrm{D}}\right\|_{\mathrm{F}}=\left\|\boldsymbol{R}_{1}-\boldsymbol{Q}_{\mathrm{A}} \boldsymbol{Q}_{\mathrm{D}}\right\|_{\mathrm{F}}=& \\\left\|\boldsymbol{V}_{1} \boldsymbol{S}_{\mathrm{R}}-\boldsymbol{Q}_{\mathrm{A}} \boldsymbol{Q}_{\mathrm{D}}\right\|_{\mathrm{F}}=& \\\left\|\boldsymbol{V}_{1}-\boldsymbol{Q}_{\mathrm{A}} \boldsymbol{Q}_{\mathrm{D}}\left\{\boldsymbol{S}_{\mathrm{R}}\right\}^{\mathrm{H}}\right\|_{\mathrm{F}}=& \\\left\|\boldsymbol{V}_{1}-\boldsymbol{Q}_{\mathrm{A}} \widetilde{\boldsymbol{Q}}_{\mathrm{D}}\right\|_{\mathrm{F}} \end{array} $

(17)

等式第3步成立的条件是因为F范数在矩阵旋转下保持不变，且有$ \widetilde{\boldsymbol{Q}}_{\mathrm{D}}=\boldsymbol{Q}_{\mathrm{D}}\left\{\boldsymbol{S}_{\mathrm{R}}\right\}^{\mathrm{H}}$.

将式(17)代入式(10)可得

$ \begin{aligned}\left(\boldsymbol{Q}_{\mathrm{A}}^{\mathrm{opt}}, \boldsymbol{G}_{\mathrm{D}}^{\mathrm{opt}}\right)=& \underset{\boldsymbol{Q}_{\mathrm{A}}, \tilde{\boldsymbol{Q}}_{\mathrm{D}}}{\arg \min }\left\|\boldsymbol{V}_{1}-\boldsymbol{Q}_{\mathrm{A}} \widetilde{\boldsymbol{Q}}_{\mathrm{D}}\right\|_{\mathrm{F}} \\ \text { s.t. } \quad &\left|\left\{\boldsymbol{Q}_{\mathrm{A}}\right\}_{i, j}\right|=1 / \sqrt{N_{\mathrm{t}}}, \\ & \operatorname{tr}\left(\boldsymbol{Q}_{\mathrm{A}} \widetilde{\boldsymbol{Q}}_{\mathrm{D}} \boldsymbol{Q}_{\mathrm{D}}^{\mathrm{H}} \widetilde{\boldsymbol{Q}}_{\mathrm{A}}^{\mathrm{H}}\right) \leqslant N_{\mathrm{s}} \end{aligned} $

(18)

至此，目标函数式(10)得到了有效的转化.

2.4 优化目标函数求解

观察式(18)，虽然Q_A和Q_D是相互耦合的，但由于Q_A的元素有恒模约束，故可通过解耦方式分别设计Q_A和Q_D^[6]，即当设计Q_A时, Q_D保持不变，反之亦然.因为α_t(Φ_i^t)的恒模量的元素满足$\left|\left\{\boldsymbol{Q}_{\mathrm{A}}\right\}_{i, j}\right|=1 / \sqrt{N_{\mathrm{t}}} $的约束，加之V₁的列向量构成了信道行向量空间的正交基，因此V₁可以看作α_t(Φ_i^t)的线性组合.通过$\boldsymbol{Q}_{\mathrm{A}} \widetilde{\boldsymbol{Q}} $逼近V₁，可得到Q_A和Q_D的最优解.为此必须合理地从α_t(Φ_i^t)中找到“最佳”的N_t^RF个阵列响应向量构成Q_A的列，故模拟预编码的设计问题可以转换为

$ \boldsymbol{T}=\underset{\boldsymbol{T}}{\arg \min } \| \boldsymbol{V}_{1}-\boldsymbol{A}_{\rm{t}} \boldsymbol{T} \widetilde{\boldsymbol{Q}}_{\bf{D}} \|_{\mathrm{F}} \\ \text { s.t. }~~~ \left\|\operatorname{diag}\left(\boldsymbol{T} T^{\mathrm{H}}\right)\right\|_{0}=N_{\mathrm{t}}^{\mathrm{RF}} \\~~~~~~~~ \operatorname{tr}\left(\boldsymbol{A}_{\rm{t}} \boldsymbol{T} \widetilde{\boldsymbol{Q}}_{\mathrm{D}} \boldsymbol{D}_{\mathrm{D}}^{\mathrm{H}} \boldsymbol{T}^{\mathrm{H}} \boldsymbol{A}_{\mathrm{t}}^{\mathrm{H}}\right) \leqslant N_{\mathrm{s}} $

(19)

其中：A_t=[α_t(Φ₁^t), α_t(Φ₂^t)，… α_t(Φ_L^t)]是一个N_t×L的矩阵，稀疏约束‖diag(TT^H)‖₀=N_t^RF表明T不可能有超过N_t^RF非零行.当T只有N_t^RF非零行时，A_t中N_t^RF非零列才能被有效地选出作为模拟预编码矩阵.

式(19)是一个稀疏重建问题，能够通过基追踪^[6]的方法求解.当模拟预编码计Q_A确定后，数字预编码设计问题可转换为求F范数最小化问题，即

$ \begin{array}{c}{\boldsymbol{Q}_{\mathrm{D}}^{\mathrm{opt}}=\arg \min \limits_{\tilde{\boldsymbol{Q}}_{\mathrm{D}}}\left\|\boldsymbol{V}_{1}-\boldsymbol{Q}_{\mathrm{A}} \widetilde{\boldsymbol{Q}}_{\mathrm{D}}\right\|_{\mathrm{F}}} \\ {\text { s.t. } \quad \operatorname{tr}\left(\boldsymbol{Q}_{\mathrm{A}} \widetilde{\boldsymbol{Q}}_{\mathrm{D}} \widetilde{\boldsymbol{Q}}_{\mathrm{D}}^{\mathrm{H}} \boldsymbol{Q}_{\mathrm{A}}^{\mathrm{H}}\right) \leqslant N_{\mathrm{s}}}\end{array} $

(20)

式(20)的最优解有一个最小二乘法^[11]的形式，即

$ \widetilde{\boldsymbol{Q}}_{\mathrm{D}}=\left\{\boldsymbol{Q}_{\mathrm{A}}\right\}^{\dagger} \boldsymbol{V}_{1} $

(21)

进一步有

$ \boldsymbol{Q}_{\mathrm{D}}=\widetilde{\boldsymbol{Q}}_{\mathrm{D}} \boldsymbol{S}_{\mathrm{R}}=\left\{\boldsymbol{Q}_{\mathrm{A}}\right\}^{\dagger} \boldsymbol{V}_{1} \boldsymbol{S}_{\mathrm{R}} $

(22)

根据最小二乘法矩阵的推导可知

$ \boldsymbol{Q}_{\mathrm{D}}=\left(\boldsymbol{Q}_{\mathrm{A}}^{\mathrm{H}} \boldsymbol{Q}_{\mathrm{A}}\right)^{-1} \boldsymbol{Q}_{\mathrm{A}}^{\mathrm{H}} \boldsymbol{V}_{1} $

(23)

根据以上分析，“最佳”的模拟预编码矩阵的选择问题是一个稀疏重建问题，通过基追踪的原理可以求解.得到模拟预编码后，利用最小二乘法最优解方法可得到最优的数字预编码矩阵Q_D^opt.

3 基于GMD的混合预编码优化算法 3.1 全连接结构下的优化算法

全连接结构下，混合预编码仅考虑基站端的编码，用户接收机可以根据接收信号进行相应的解码处理，式(18)的最优解算法由2个环节构成，前者通过for循环将GMD变换得到的残差矩阵Q₁作为最优预编码矩阵，G₁^H作为合并矩阵代入OMP方法，得到Q_A和Q_D.后者对Q_D执行引理1对应的变换，并对有效预编码矩阵进行归一化，以满足发射功率的约束.

算法1   伪代码

输入：基于GMD的最优预编码矩阵Q_res，发射端射频链数N_t^RF，发射天线数N_t，接收天线数N_r，阵列响应向量矩阵A_t；

输出：模拟预编码矩阵Q_A，数字预编码矩阵Q_D；

初始化：计算[S₁V₁D₁]=SVD(H)，[Q R P]=GMD(S₁ V₁ D₁), Q_A=空矩阵，Q_res=P(:, 1:N_s)；

For i≤N_t^RF

${\mathit{\boldsymbol{A}}_{\rm{t}}} = 1/\sqrt {{N_{\rm{t}}}} {{\rm{e}}^{\left( {{\rm{jangle }}\left( {{S_1}} \right)} \right)}} $

Φ=A_t^HQ_res；k=arg max_{l=1, …，L}(ΦΦ^H)_{l, l}；

  Q_A=[Q_A, A_t(:, k)]; ；

Q_D=(Q_A^HQ_A)^-1Q_A^HV₁；

$\boldsymbol{Q}_{\mathrm{res}}=\frac{\boldsymbol{Q}_{\mathrm{res}}-\boldsymbol{Q}_{{\rm A}} \boldsymbol{Q}_{\mathrm{D}}}{\left\|\boldsymbol{Q}_{\mathrm{res}}-\boldsymbol{Q}_{{\rm A}} \boldsymbol{Q}_{\mathrm{D}}\right\|_{\mathrm{F}}}; $

End For

根据实现引理1转换关系生成S_R，得到Q_D=Q_DS_R；

归一化$ {\mathit{\boldsymbol{Q}}_{\rm{D}}} = \sqrt {{N_{\rm{s}}}} \frac{{{\mathit{\boldsymbol{Q}}_{\rm{D}}}}}{{{{\left\| {{\mathit{\boldsymbol{Q}}_{\rm{A}}}{\mathit{\boldsymbol{Q}}_{\rm{D}}}} \right\|}_{\rm{F}}}}}$

需要指出的是，由于运用引理1中的转换关系进行计算，过程中不需要计算S_R，仅仅是在Q_D的每个阶段都应用相应的置换和乘法运算即可.因此，生成Q_D的运算复杂度为O((N_s+N_t)N_s)^[15]，相应的算法1的复杂度为O((N_t^RF)²N_tN_s).而Golub-Kahan双对角化方案^[16](通常是计算SVD的第1步)的计算复杂度为O(N_sN_tK)，这表明基于GMD的混合预编码在优化系统频效的算法复杂度方面与传统的基于SVD的混合预编码相比只会额外增加较小的算法复杂度，这是因为需要计算Q_A的伪逆.就整体系统复杂度而言，运用该算法1的GMD预编码方案能有效避免复杂的比特分配问题，降低编/解码的难度，复杂度远远低于基于SVD预编码方案.

3.2 部分连接结构下的优化算法

部分连接结构下，混合预编码最优解算法的前一环节通过选择矩阵G₀将信道H进行变换得到所需的辅助矩阵G^[11].后一环节根据文献[11]中部分连接结构下模拟和数字预编码之间的关系，利用GMD变换得到的酉矩阵进一步计算出该变换下符合条件的Q_A和Q_D，然后对Q_D执行引理1对应的变换，并对有效预编码矩阵进行归一化以满足发射功率的约束.假设每个链连接的天线数M=N_t/N_t^RF，基站采用K个RF链去传输K个数据流，即K=N_t^RF=N_s，且基站拥有完全的信道状态信息H.

算法2   伪代码

输入：信道矩阵H，发射天线数N_t，接收天线数N_r；

输出：模拟预编码矩阵Q_A，数字预编码矩阵Q_D；

初始化：计算G₀=H^Hinv(eye(N_r))H，

G=[eye(N_s), zeros(N_s, N_s(N_t^RF-1))]G₀×[eye(N_s), zeros(N_s, N_s(N_t^RF-1))]^H，

  For i≤N_t^RF

    [S V D]=SVD(G)

    [Q R P]=GMD(S V D)

    v₁=P(:, 1);

    μ=R(1, 1);

    $a(:, i)=1 / \sqrt{N_{{\rm t}}} \mathrm{e}^{\left(\text {jangle }\left(V_{1}\right)\right)} $；

    Q_A=a(:, 1)；

    $d(i)=\operatorname{norm}\left(\boldsymbol{v}_{1}, 1\right) / \sqrt{N_{\mathrm{t}}} $；

    p(:, i)=(1/N_s)norm(v₁, 1)×e^{(jangle(v₁));}

    $ \boldsymbol{G}=\boldsymbol{G}-\frac{\left(\rho / N \sigma^{2}\right) \mu^{2} \boldsymbol{v}_{1} \boldsymbol{v}_{1}^{\mathrm{H}}}{1+\left(\rho / N \sigma^{2}\right) \mu}$

  End For

  Q_D=diag(d);

根据实现引理1转换关系生成S_R，得到Q_D=Q_DS_D；

归一化$\boldsymbol{Q}_{\mathrm{D}}=\sqrt{N_{\mathrm{s}}} \frac{\boldsymbol{Q}_{\mathrm{D}}}{\left\|\boldsymbol{Q}_{\mathrm{A}} \boldsymbol{Q}_{\mathrm{D}}\right\|_{\mathrm{F}}}$

上述算法中, 生成辅助矩阵G的运算复杂度为O(M²(N_t^RFS+N_r))^[17]，生成Q_D的运算复杂度为O((K+N_t)K)，所以算法2的复杂度为O(K²(N_t^RFS+N_r)+K²+N_tK)，而El Ayach等^[6]所提的算法复杂度为O((N_t^RF)⁴M+(N_t^RF)²L²+(N_t^RF)²M²L)，考虑典型的毫米波通信系统中N_t^RF=8，M=8，N_t=64，N_r=16，L=3，S=5^[11].通过分析上述的复杂度解析式可知，所提算法复杂度较El Ayach等^[6]所提算法复杂度更低，这说明GMD在处理部分连接结构应用上复杂度也有较好的表现.

4 仿真结果分析

通过仿真来分析基于GMD的混合预编码方案与空间稀疏预编码的性能.仿真环境设置如下：基站采用ULA发射天线阵列，天线数分别为64和256，用户端天线数对应为16和64，天线间隔d=λ/2.基站和用户端的射频链个数均为N_t^RF=N_r^RF=8，载波频率为28 GHz.采用S-V信道模型，有效路径数L=3，每条路径的复增益服从分布CN(0, 1)，两端天线的方位角AoA和AoD服从在[-π/2, π/2]上的均匀分布，信噪比为ρ/σ²n.对于最优无约束预编码方案，采用注水功率分配方案.对于基于SVD和GMD预编码方案中所有的子信道均采用16QAM的调制方法.

图 3所示为发射天线数为256，接收端天线数为64时所提算法1在不同迭代次数下的频效性能曲线.从图 3可以看出，随着迭代次数的增加，系统频效逐渐增加.当迭代次数达到100时，算法1基本收敛.说明在应用GMD信道处理方法下，所提算法对于系统频效的可行性.

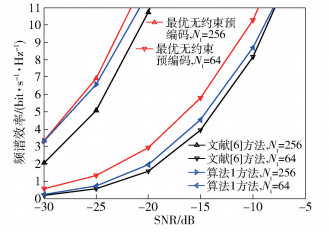
图 4所示为在两端射频链数均为8，传输数据流N_s=4时，基站天线数不同时的频效随SNR的变化趋势.从图中可以看出：1)基于GMD的混合预编码方法在基站天线数目不同时所获得的系统频效均优于El Ayach等^[6]提出的方案；2)随着发射天线数的增加，系统频效逐渐增加；随着SNR的增加，频效增幅逐渐变大，这说明天线规模越大，频效性能越好，但因为有最大发射功率的限制，故频效增幅有极值；3)基站天线数目增加到一定值时，所提方案能接近最优预编码的性能.

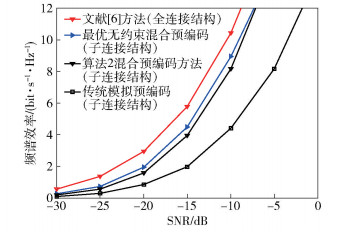
图 5所示为在两端射频链数均为8，传输数据流N_s=4，发射天线数为64时，2种天线连接方式下系统频效性能随SNR的变化趋势.从图中可以看出：1)在部分连接结构下，基于GMD的混合预编码方案的性能均优于传统模拟预编码；2)所提预编码方案的频效性能与该传输结构下的最优预编码方案相当，说明所提方案达到了近优性能；3)当SNR达到10 dB时，所提方案在部分连接传输结构下的频效性能近似达到了在全连接结构下El Ayach等^[6]所提方案的80%.综合考虑笔者所提方案在保证系统复杂度基础上，具有良好的可拓展性和较好的频效性能.

5 结束语

针对奇异值分解下的不同子信道信噪比变化较大，导致系统复杂度增加和编/解码难度加大的问题，提出基于GMD的混合预编码方案.与El Ayach等^[6]所提方案相比，提出的预编码方案能有效地均衡子信道信噪比从而降低系统整体的复杂度.同时，为了更好地应用于实际通信场景，将该编码拓展到部分连接传输结构中，也得到了较好的频效性能.仿真结果表明，所提出的混合预编码方案在不同基站天线数目下的频效性能均优于正交匹配追踪^[6]方案，且可以应用于现有的2种传输结构，应用性较强.

此外，提出的算法及结论是在理想信道状态下得出的，对于在更加复杂的更普适的通信场景中的算法和结论尚需进一步研究.