提出了一种基于主成分分析的图像哈希算法.采用主成分分析对样本进行降维,取位于变换矩阵顶端最具有识别信息的少量特征向量构造投影矩阵,再对降维后样本进行局部保持映射,同时,对主成分分析投影矩阵进行随机旋转,形成多个小投影矩阵,采用矩阵拼接方法将小投影矩阵合并构造编码投影矩阵;最后,将训练样本投影到编码投影矩阵,得到降维样本,并对其进行哈希编码,得到最终的二进制编码.实验结果证明,同其他经典算法相比,该算法具有较好的稳定性,可降低内存消耗,并提高效率.
A novel image Hashing based on principal component analysis (PCA) was proposed. PCA was introduced to reduce dimension of samples, and the projection matrix was achieved by choosing several eigenvectors which have higher recognition ability. Based on which, the reduced-sample was mapped with locality preserving projection (LPP). Meanwhile, the projection matrix of principal component analysis was randomly rotated to form a series of transformational matrixes. The matrix stitching was adopted to construct the final code projection matrix. Finally, the original samples were projected into the code projection matrix to get a reduced dimensional sample, and the Hashing code was used to achieve the final binary encoding. Experiments show that the proposed method has better stability, lower memory consumption and higher efficiency compared with other traditional methods.
哈希技术能够将原特征编码成紧致的二值哈希码,大幅降低内存消耗,同时可以缩减查询所需时间,近年来备受关注.基于数据独立的局部敏感哈希(LSH,locality sensitive Hashing)[1]及其改进算法被认为是在高维空间中快速搜索的重要突破之一,但是随着编码位数的增加会降低检索效率,同时,多个哈希表还会增大CPU的存储空间和查询响应时间.数据依赖哈希技术[2-9]主要依赖原始数据的内部结构把高维数据投影到低维空间中,通常被证明比数据独立的LSH更有效.
提出了一种基于主成分分析(PCA,principal component analysis)[10]的局部保持哈希算法RPLPH(rotation PCA locality preserving Hashing).首先采用PCA对样本进行降维,取位于变换矩阵顶端最具有识别信息的少量特征向量构造PCA投影矩阵,在此基础上对PCA降维样本进行局部保持投影(LPP,locality preserving projection)[11],同时利用随机正交矩阵对PCA降维矩阵进行多次随机旋转,构造多个LPP投影矩阵,然后融合二进制编码分段思想[12],把这些小矩阵拼接构造最终的投影矩阵.最后将原始样本投影到该矩阵上进行哈希编码.算法中,把PCA和LPP有效结合,保留了原始数据局部和全局的相似性结构,而且把随机旋转应用于PCA数据的顶部主要投影中,减少了编码之间的量化误差,使得投影矩阵更加多样化.同时,流形子空间特征提取与随机旋转的巧妙融合在很大程度上提高了处理效率.大量实验结果证明了该方法的可行性和高效性.
1 相关理论 1.1 PCAPCA[10]是一种经典的无监督线性子空间特征提取方法.优化目标函数可写成:
| $ \mathop {\text {argmaxtr}}\limits_\mathit{\boldsymbol{W}} \left( {{\mathit{\boldsymbol{W}}^{\rm{T}}}\mathit{\boldsymbol{X}}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{W}}} \right){\rm{s}}{\rm{. t}}{\rm{. }}{\mathit{\boldsymbol{W}}^{\rm{T}}}\mathit{\boldsymbol{W}} = \mathit{\boldsymbol{I}} $ | (1) |
其中: X={x1,x2,…,xn}∈Rd×n为样本矩阵,n和d分别表示样本点的数目和样本点的维数;WT为W的转置矩阵,在约束条件WTW=I下,满足最大化目标函数的矩阵W就是经过PCA降维后得到的投影矩阵.利用拉格朗日乘子法可得到如下的广义特征值求解问题:
| $ \mathit{\boldsymbol{X}}{\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{w}}_i} = {\mathit{\boldsymbol{\lambda }}_i}{\mathit{\boldsymbol{w}}_i} $ | (2) |
假定w1,w2,…,wt为式(2)最大的t个特征值对应的特征向量,则PCA投影矩阵表示为W=[w1,w2,…,wt]∈Rd×t.样本集X的低维特征表示为yi=WTxi,i=1,2,…,n.
1.2 LPPLPP[11]作为一种基于流形的子空间提取方法,其基本思想就是寻找一个投影矩阵V,将高维空间Rd中的样本集X=[x1,x2,…,xn]映射为低维空间Rt(t < d)中的样本集Y=[y1,y2,…,yn],即yi=VTxi,i=1,2,…,n,而且在Rd空间内互为近邻的两点经V映射后在Rt空间中仍互为近邻.其目标函数为
| $ \sum\limits_{ij} {{{\left( {{\mathit{\boldsymbol{y}}_i} - {\mathit{\boldsymbol{y}}_j}} \right)}^2}} {\mathit{\boldsymbol{M}}_{ij}} $ | (3) |
通过简单的代数运算,目标函数(式(3))可以简化为
| $ \begin{array}{*{20}{c}} {\frac{1}{2}\sum\limits_{ij} {{{\left( {{\mathit{\boldsymbol{y}}_i} - {\mathit{\boldsymbol{y}}_j}} \right)}^2}} {\mathit{\boldsymbol{M}}_{ij}} = }\\ {\frac{1}{2}\sum\limits_{ij} {{{\left( {{\mathit{\boldsymbol{V}}^{\rm{T}}}{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{V}}^{\rm{T}}}{\mathit{\boldsymbol{x}}_j}} \right)}^2}} {\mathit{\boldsymbol{M}}_{ij}} = }\\ {{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{X}}(\mathit{\boldsymbol{D}} - \mathit{\boldsymbol{M}}){\mathit{\boldsymbol{X}}^{\rm{T}}} = }\\ {{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{XL}}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{V}}} \end{array} $ | (4) |
其中: Mij为近邻图的权值矩阵,如果xi与xj之间有一条边相连,Mij=exp(-‖xi-xj‖2/2δ2);否则Mij=0;矩阵D是一个对角矩阵,其值为权值矩阵M每一行或每一列的数据元素之和,即
| $ \mathop {\text{argmin}}\limits_\mathit{\boldsymbol{V}} {\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{XL}}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{V}}\;{\rm{s}}{\rm{. t}}{\rm{. }}{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{XD}}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{V}} = 1 $ | (5) |
经LPP投影后的变换矩阵就是式(5)求解后最小的t个特征值对应特征向量构成的V={v1,v2,…,vt}.
2 基于PCA的图像哈希假设给定一个数据X={x1,x2,…,xn}∈Rd×n,构造基于PCA的图像哈希具体步骤主要包括3部分.
2.1 PCA降维对样本的协方差矩阵XXT进行PCA降维处理,在PCA中,数据的大部分信息是由少量较大的特征向量捕获的,降维后的较小特征值对应的特征向量往往是噪音.因此算法中只保留W顶端r(r < t)个特征向量,得到正交矩阵A.将该样本投影到正交矩阵A上得到PCA降维后的样本Y,即
| $ \mathit{\boldsymbol{Y}} = {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{X}} $ | (6) |
其中:A=[a1,a2,…,ar],A∈Rd×r.然后利用随机正交矩阵R(i)∈Rr×r(i=1,2,…,K)对A进行旋转.其中随机旋转一方面使得哈希编码间的量化误差最小;另一方面增加了A顶端特征向量的多样性.此时把得到的正交矩阵记为
| $ \mathit{\boldsymbol{B}} = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{R}}^{(i)}},i = 1,2, \cdots ,K $ | (7) |
其中K=t/r表示进行K次旋转.
2.2 LPP投影算法中将式(6)中的投影矩阵Y∈Rr×n进行LPP变换,构造最终的变换矩阵,其中Y是经过PCA投影之后得到的降维样本.把Y代入式(5)中得出新的目标函数如下:
| $ \mathop {\text{argmin}}\limits_\mathit{\boldsymbol{C}} {\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{YL}}{\mathit{\boldsymbol{Y}}^{\rm{T}}}\mathit{\boldsymbol{C}}\ {\rm{ s}}{\rm{.t}}{\rm{. }}\ \ {\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{YD}}{\mathit{\boldsymbol{Y}}^{\rm{T}}}\mathit{\boldsymbol{C}} = 1 $ | (8) |
对式(8)求解后,C表示最小的r个特征值对应的特征向量C={c1,c2,…,cr}.利用拉格朗日乘子法可将式(8)化为
| $ L(c,\lambda ) = {\mathit{\boldsymbol{c}}^{\rm{T}}}\mathit{\boldsymbol{YL}}{\mathit{\boldsymbol{Y}}^{\rm{T}}}\mathit{\boldsymbol{C}} - \lambda \left( {{\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{YD}}{\mathit{\boldsymbol{Y}}^{\rm{T}}}\mathit{\boldsymbol{C}} - 1} \right) $ | (9) |
接着,对L(c,λ)中c和λ进行求导:
| $ \frac{{\partial L}}{{\partial c}} = \mathit{\boldsymbol{YL}}{\mathit{\boldsymbol{Y}}^{\rm{T}}}\mathit{\boldsymbol{C}} - \lambda \mathit{\boldsymbol{YD}}{\mathit{\boldsymbol{Y}}^{\rm{T}}}\mathit{\boldsymbol{C}} = 0 $ | (10) |
| $ \frac{{\partial L}}{{\partial \lambda }} = \mathit{\boldsymbol{CYL}}{\mathit{\boldsymbol{Y}}^{\rm{T}}}\mathit{\boldsymbol{C}} - 1 = 0 $ | (11) |
最终结果为
| $ \mathit{\boldsymbol{YL}}{\mathit{\boldsymbol{Y}}^{\rm{T}}}\mathit{\boldsymbol{C}} = \lambda \mathit{\boldsymbol{YD}}{\mathit{\boldsymbol{Y}}^{\rm{T}}}\mathit{\boldsymbol{C}} $ | (12) |
式(6)和式(12)联立求得新投影矩阵Q∈Rr×r:
| $ \mathit{\boldsymbol{Q}} = \mathit{\boldsymbol{AC}} $ | (13) |
用B代替式(13)中的A.式(13)便化为
| $ {\mathit{\boldsymbol{Q}}^{(i)}} = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{R}}^{(i)}}\mathit{\boldsymbol{C}},i = 1,2, \cdots ,K $ | (14) |
得到含有r个特征向量的K个投影矩阵块.把K个投影矩阵块Q(i)拼接成最终的投影矩阵V.
2.3 哈希编码得到最终的投影矩阵后,将原始样本X投影到V上,得到低维样本数据.利用式(15)所示的哈希函数对低维样本进行0或1的二值编码,得到最终的二进制码.
| $ \mathit{\boldsymbol{H}} = \text{sign}\left( {{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{X}}} \right) $ | (15) |
为验证本文算法的性能,在Win8系统Matlab R2016a环境下,采用3个国际上通用的人脸图像数据库AR、ORL和Yale进行了几组实验.
3.1 r参数选取实验实验中,通过改变特征向量的数目r来测试它对算法模型的影响. 图 1给出了3个数据集下r从2~32情况下RPLPH的平均检索精度(MAP,mean average precision)值.可以看出,RPLPH的检索性能因r的不同会发生改变.当r的取值较大时,降维矩阵引入了更多的噪音,降低了性能.当r的取值较小时,降维矩阵块中只提取了较少的特征向量,捕获PCA投影数据的结构信息远远不够,因而性能并不能改善.实验结果显示,当特征向量个数取中间值时,RPLPH方法性能较好.
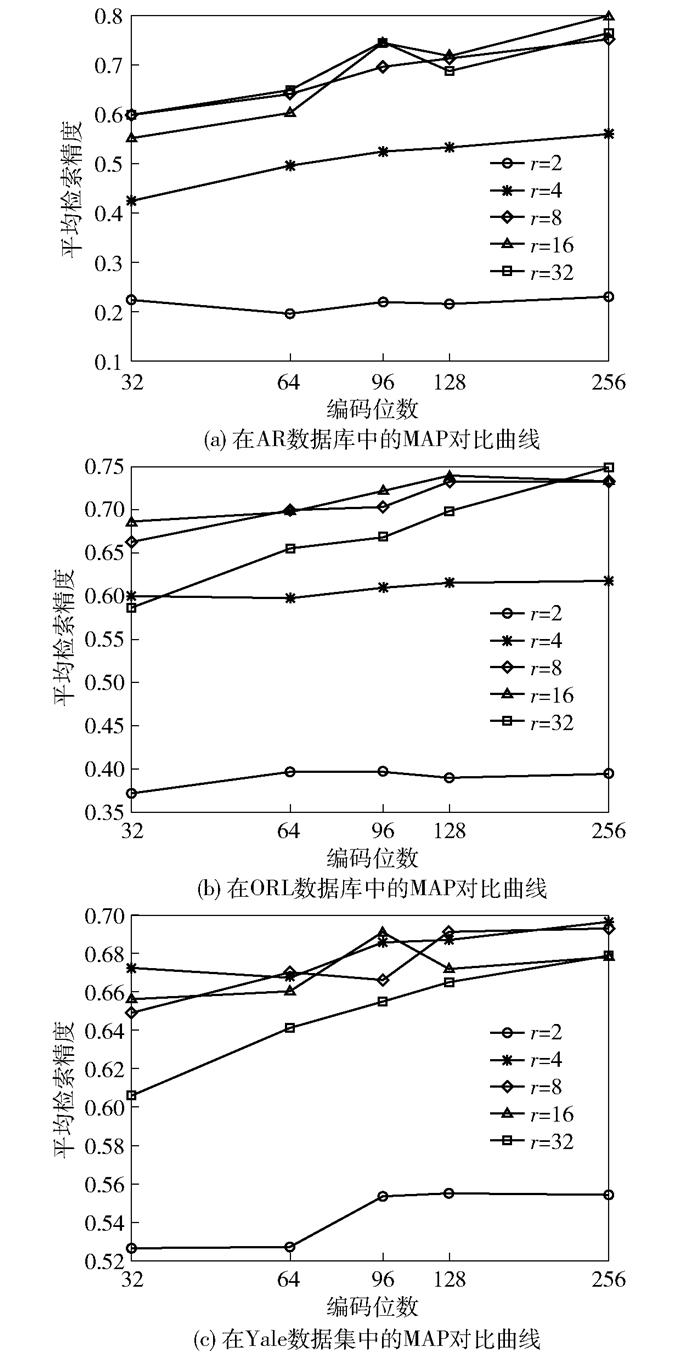
|
图 1 3个数据集中本文算法的性能随r取值不同的MAP曲线 |
为验证算法的性能,将原始样本与采用本文算法、仅在PCA降维后的子空间中进行LPP映射算法(LPPH,LPP Hashing)以及仅基于PCA随机旋转(LPP-RR,LPP random rotation)3种方法进行了对比实验,实验的MAP曲线如图 2所示.可以看出,由于本文算法在PCA降维时只选取少量的特征向量,减少了投影过程中不必要的噪声.随机旋转减少了编码之间的量化误差,因此,本文算法比LPP-RR和LPPH要占优势.同时,在ORL数据库中,将本文算法与LPPH和LPP-RR 2种算法的训练时间进行了对比实验.结果如表 1所示.可以看出,本文算法的训练时间较少,尤其在32 bit和64 bit时效果更明显.
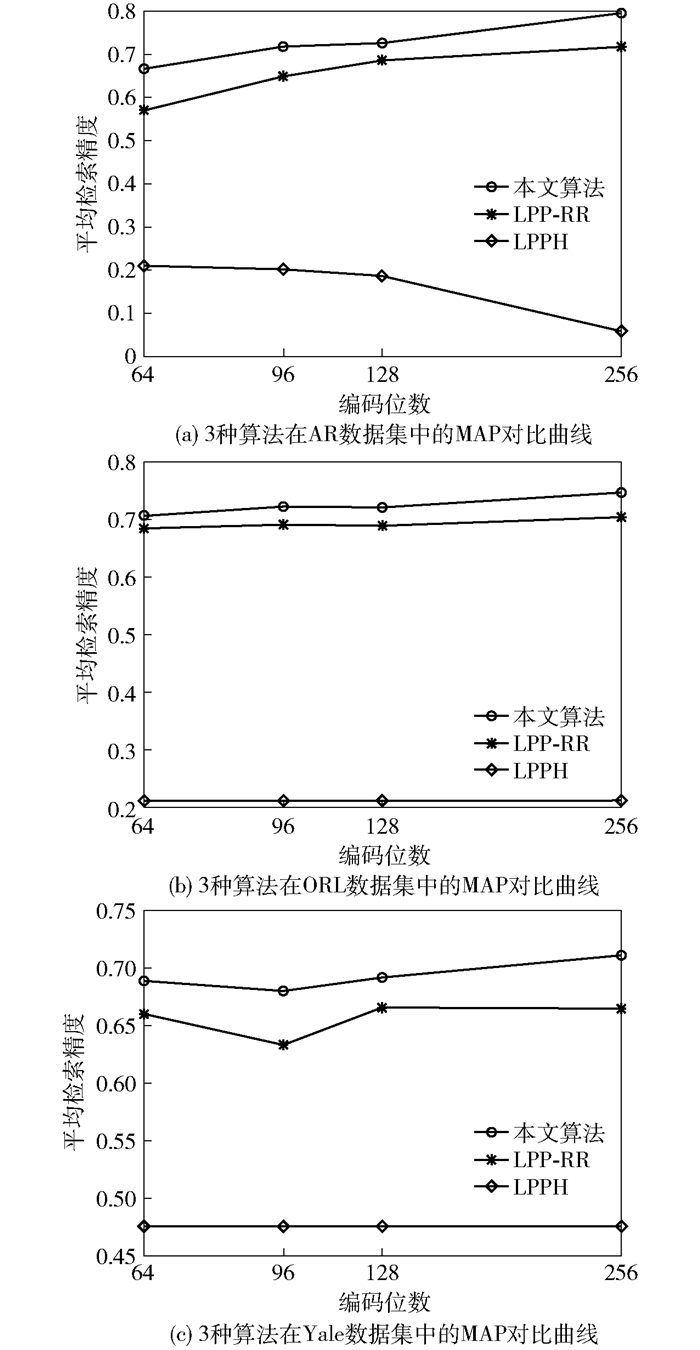
|
图 2 3种算法在3个数据集上的MAP对比曲线 |
|
|
表 1 3种算法下ORL的时间复杂度对比结果 |
将本文算法与7种经典哈希方法LSH[1]、PCA哈希(PCAH[2],PCA Hashing)、球哈希(SpH[3],spherical Hashing)、谱哈希(SH [4],spectral Hashing)、迭代量化(ITQ[5],iterative quantization)、随机旋转PCA(PCA-RR[6],PCA random rotation)、两层随机主映射哈希(R2PCAH[7],two-fold randomness principal projection Hashing)进行了对比. 表 2给出了8种方法在3个数据集下分别进行96、128和256位编码的MAP数值.可以看出,本文算法的MAP数值最高.对PCAH而言,由于在进行PCA降维时的噪音信息使得其随着编码位数的增加,其MAP值逐渐减少,而RPLPH在PCA投影时仅提取了少量有用的信息从而成功地避免了这个现象. PCA-RR采用随机正交矩阵对PCA进行旋转,使得编码间的量化误差最小,其检索性能提升.而本文算法同样引入随机正交矩阵对PCA顶部特征向量进行随机旋转,可以获取多种投影矩阵,减少了编码间的量化误差,具有较高的检索性能. 图 3给出了8种方法在ORL数据集上的P-R曲线.可以看出,本文算法同样具有较好的性能. PCAH方法随着编码长度的增加曲线迅速地下降,其重要的原因是在PCA进行特征值分解的时候引入了一些噪音,编码位数越大,其引入的噪音越多,性能越差.本文算法充分地利用随机旋转而且只取PCA处理后的最顶部具有辨识度的特征向量,有效地解决了传统LPP在基于哈希图像处理中出现的低效、耗时等缺点.
|
|
表 2 3个数据集下8种方法不同编码长度的MAP对比值 |
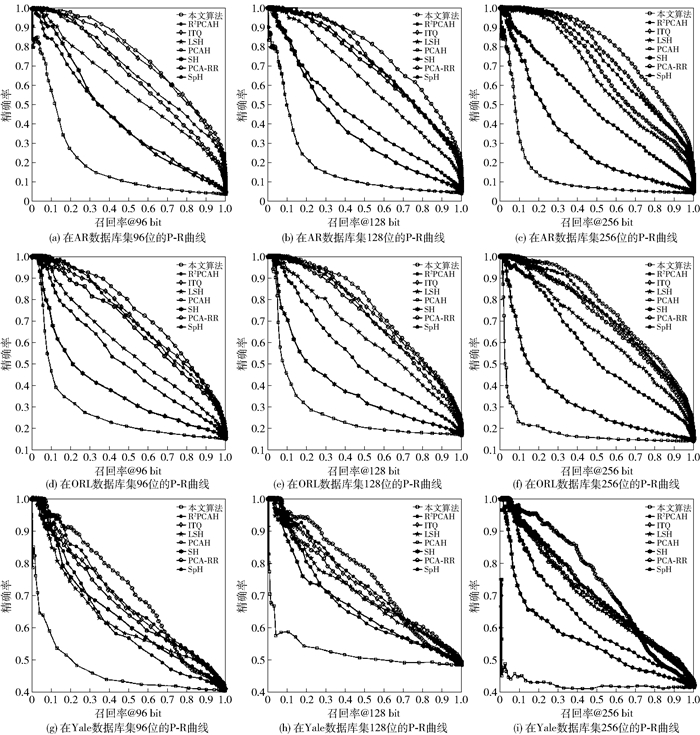
|
图 3 3个数据集下8种方法不同编码长度时的对比曲线 |
提出了一种图像哈希算法,首先对样本进行PCA变换,再对降维样本进行LPP变换,并利用随机正交矩阵对PCA变换后最高位的部分特征向量进行随机旋转,以减少编码间的量化误差.最后把得到的多个小投影矩阵拼接,构造最终的投影矩阵,训练样本经过该投影矩阵降维后利用哈希函数得到哈希编码.该方法能够在投影过程中保持数据的全局结构和局部信息,有效解决LPP直接用于哈希图像处理中存在的问题.实验结果证明,该算法取得了较好的效果.
| [1] |
Gionis A, Indyk P, Motwani R. Similarity search in high dimensions via Hashing[C]//VLDB'99. Edinburgh: IEEE, 1999: 518-529.
|
| [2] |
Wang J, Kumar S, Chang S. Semi-supervised Hashing for scalable image retrieval[C]//CVPR'10. San Francisco: IEEE, 2010: 3424-3431.
|
| [3] |
Heo J, Lee Y, He J, et al. Spherical Hashing[C]//CVPR'12. Rhode: IEEE, 2012: 2957-2964.
|
| [4] |
Weiss Y, Torralba A, Fergus R. Spectral Hashing[C]//NIPS'08. Vancouver: Elsevier, 2008: 1753-1760.
|
| [5] |
Gong Y, Lazebnik S. Iterative quantization: a procrustean approach to learning binary codes[C]//CVPR'11. Colorado Springs: IEEE, 2011: 817-824.
|
| [6] |
Jegou H, Douze M, Schmid C, et al. Aggregating local descriptors into a compact image representation[C]//CVPR'10. San Francisco: IEEE, 2010: 3304-3311.
|
| [7] |
Li P, Ren P. R2PCAH:Hashing with two-fold randomness on principal projections[J]. Neurocomputing, 2017(235): 236-244. |
| [8] |
李金凤, 吴涛, 王宏霞. 基于MFCC相关系数的语音感知哈希认证算法[J]. 北京邮电大学学报, 2015, 38(2): 89-93. Li Jinfeng, Wu Tao, Wang Hongxia. Perceptural Hashing based on correlation coefficient of MFCC for speech authentication[J]. Journal of Beijing University of Posts and Telecommunications, 2015, 38(2): 89-93. |
| [9] |
张秋余, 省鹏飞, 黄羿博, 等. 多格式音频感知哈希算法[J]. 北京邮电大学学报, 2016, 39(4): 77-82. Zhang Qiuyu, Xing Pengfei, Huang Yibo, et al. Perceptual Hashing algorithm for multi-format audio[J]. Journal of Beijing University of Posts and Telecommunications, 2016, 39(4): 77-82. |
| [10] |
Abdi H, Williams L J. Principal component analysis[J]. Wiley Interdisciplinary Reviews:Computational Statistics, 2010, 2(4): 433-459. DOI:10.1002/wics.101 |
| [11] |
He X, Niyogi P. Locality preserving projections[C]//NIPS'04. Vancouver: ACM, 2003: 153-160.
|
| [12] |
Leng C, Cheng J, Yuan, X, et al. Learning binary codes with bagging PCA[C]//ECML'14. Nacy: Springer, 2014: 177-192.
|



