针对空间调制系统的最大似然算法复杂度较高的问题,提出一种改进的最大比合并算法.定义一种权重因子,其下标对应发射天线序号;通过对权重因子的值进行降序排列,选取前L个值所对应的天线组成天线候选集,假设天线候选集中的某一根天线被激活,利用迫零算法计算该天线下的发送符号;最后对天线候选集中所有天线和对应的估计符号进行最大似然搜索.仿真结果表明,所提出的新算法在保证次优检测性能的前提下,明显降低了算法的复杂度.
Aiming at the high complexity of the maximum likelihood detection algorithm for spatial modulation systems, an improved maximum ratio combing algorithm was proposed. In this algorithm, a weighting factor was defined, whose subscript corresponded to the sequence number of transmitting antenna. Then the values of the weighting factor were sorted in descending order, and the antennas corresponding to the first L values were selected to form the antenna candidate set. Assuming that an antenna in the antenna candidate set was activated, the possible transmit signal was calculated by zero forcing algorithm. Maximum likelihood search was performed for all antennas and corresponding estimation symbols in the antenna candidate set. Simulation results show that the proposed algorithm can significantly reduce the complexity of the algorithm on the premise of ensuring the sub-optimal detection performance.
随着用户数量和无线通信业务的急剧增长,现有的通信网络已经不能满足需要.未来无线通信网络将面临高系统容量和高频谱利用率的巨大挑战,有限的通信资源与日益增长的通信业务需求之间的矛盾已经成为未来移动通信亟待解决的问题.多输入多输出(MIMO, multiple input multiple output)技术[1]通过在收发端布置多根天线,在保证系统传输可靠性的前提下,可以大幅度提高数据传输速率和频谱利用率,能够很好地解决上述问题.然而,多天线技术也带来了信道间干扰,天线间同步和接收端检测算法复杂度较高等问题,这给MIMO技术的实际应用带来了一些困难.空间调制(SM, spatial modulation)技术[2]作为一种新的MIMO技术,既克服MIMO技术的缺陷,同时又不增加系统成本.
目前对于SM系统接收端的信号检测算法的研究已有不少成果. Ntontin等[3]给出的最大似然准则(ML, maximum likelihood)算法,通过搜索所有的发射天线和符号,可以达到最佳的检测性能,但是随着发射天线数的增加和调制阶数的增加,ML算法的复杂度急剧上升.门宏志等[4]提出与调制阶数无关的ML简化算法,在估计发送符号时,从矢量量化的角度出发,直接对发送符号进行量化解调,极大地降低了算法复杂度,但是该算法只适用于MPSK调制方式. Zhang等[5]借鉴树搜索的思想,提出了基于M值的ML算法,通过从树形结构图的第一层搜索到最后一层的方式来寻找最优解,这种算法的检测结果受每层保留节点数和计算顺序的影响较大,并且忽略了对误码率性能的影响. Peng等[6]给出的最大比合并(MRC, maximum ratio combing)算法,对激活天线序号和发送的信号分开进行检测,但是MRC算法假设信道矩阵的列范数都是一样的,只适用于一些特殊信道. Wang等[7]提出了一种新的基于信号矢量(SVD, signal vector based on detection)的检测算法,它的基本原理和MRC是一样的,也是先估计激活天线序号,再估计发射信号,但是它的性能优于MRC算法,并且对信道没有要求. Lee等[8]给出了SVD算法的硬件实现方法,并对测得的数据进行了分析. Maleki等[9]对MRC算法的天线判决标准做了修正,提出了改进的最大比合并(MMRC, modified MRC)检测算法.该算法可以适用于瑞利信道,且在高信噪比时,通过该标准得到的最大值对应天线的信道增益与实际激活天线的信道增益相似度最高.此外,还有一些其他的检测算法,如压缩感知检测算法[10]、球形检测算法[11],这些算法的检测过程太过复杂,难以进行硬件实现.
在MMRC算法的基础上,提出一种改进的算法(IMMRC, improved MMRC).先对激活天线按照权重因子进行降序排序,从中取前L个组成天线候选集Ω,而候选集中的每一根天线都有可能选为被激活的发射天线.然后对候选集中的每一根天线和接收信号进行迫零检测,得到的信号为该天线上的发射信号,对候选集中的天线和对应的检测符号进行ML搜索.最后,取最小值对应的天线和信号为最终的检测结果.该算法相比MMRC算法提高了系统误码率性能,同时保持较低的复杂度.
1 系统模型考虑一个有Nt根发射天线和Nr根接收天线的空间调制系统,每时刻只激活一根天线用来传输信息.在发射端,待传输的信息比特流被分为若干个帧,每一帧传输信息流的个数为m=lbNt+lbM,第一部分lbNt个bit用来从空间域K中选择激活的天线序号i,K为空间域的天线集合,且K={1, …, Nt}.第二部分lbM个bit被映射为星座图S中的一个符号s,且S的大小为M.因此,发射的信号向量可以表示为x=[0, …, sk, …, 0]T,sk表示第k根天线被激活,并在激活的天线上发送信号s.
假定Nt=4,采用BPSK调制(M=2)的SM映射规则如表 1所示,则前lb 4=2个bit用来选择激活的天线序号,剩下的lb 2=1个bit用来映射星座图中的一个符号作为激活天线上的发送符号.
|
|
表 1 SM的映射规则 |
假设信道是准静态的平坦瑞利衰落信道,即信道在一个符号周期里保持不变,不同的符号周期之间相互独立,则接收的信号向量可以表示为
| $ \mathit{\boldsymbol{y}}{\rm{ = }}\mathit{\boldsymbol{H x}}{\rm{ + }}\mathit{\boldsymbol{n}} $ | (1) |
对于空间调制系统而言,ML算法具有最优的检测性能,它同时检测激活的天线序号和传输的符号,ML最优检测准则可以表示为
| $ \begin{aligned}(i, s)_{\mathrm{ML}} &=\underset{i \in K, s \in S}{\arg \min } p\left(\boldsymbol{y} / \boldsymbol{h}_{i}, \boldsymbol{x}\right)=\\ & \underset{i \in K, s \in S}{\arg \min }\|\boldsymbol{y}-\boldsymbol{H} \boldsymbol{x}\|_{\mathrm{F}}^{2} \end{aligned} $ | (2) |
由于在SM系统中只有一根发送天线激活用来发送信号,式(2)可以简化为
| $ (i, s)_{\mathrm{ML}}=\underset{i \in K, s \in S}{\arg \min }\left\|\boldsymbol{y}-\boldsymbol{h}_{i} s\right\|_{\mathrm{F}}^{2} $ | (3) |
其中:i、s分别表示估计的激活天线序号和发送的符号;‖·‖F2表示2范数. ML算法通过遍历搜索所有发射天线和星座符号点的联合样本空间,可以得到最优的检测性能,但是随着发射天线数的增多以及调制阶数的升高,算法的复杂度会急剧增大.
2 改进的检测算法 2.1 基于信道增益的天线MRC算法是最早的次优检测算法,但在高信噪比时检测性能较差,其改进的MMRC算法修正了天线的判决标准,可以在高信噪比时发挥不错的检测性能,但是误码率性能和ML算法相比仍有一定的差距.笔者在MMRC的基础上,将多个可能的天线组成天线候选集.在进行天线判决时,对所有的发射天线和接收信号进行一定的处理,处理方法如式(4),计算结果记为τi,i表示发射天线序号.
| $\tau_{i}=\left|\frac{\boldsymbol{h}_{i}^{\mathrm{H}} \boldsymbol{y}}{\left\|\boldsymbol{h}_{i}\right\|_{\mathrm{F}}}\right| $ | (4) |
计算所有τi并组成集合T={τ1, τ2, …, τNt}.其中当τi大表示成为激活天线的可能性也大,因此可以理解为一种权重因子.将集合T进行降序排列,即
| $ \left\{j_{1}, j_{2}, \cdots, j_{N_\text{t}}\right\}=\arg \operatorname{sort}(T) $ | (5) |
其中j1和jNt分别表示T中的最大值和最小值所对应的天线序号.为了减少搜索空间,选取前L个天线序号组成候选集Ω={j1, j2, …, jL}.激活天线相当于已经确定下来了,只需要进行发送符号检测.需要指出的是,当L=1时,即选取最大值对应的天线直接作为发射天线,此时IMMRC算法退化为MMRC算法.
2.2 基于迫零准测的符号检测假设当前第k(1≤k≤L)根天线是激活状态,在激活天线下,对第k根天线上的发送符号进行检测,可以表示为sk=hk†y,其中(·)†表示矩阵的伪逆.然后对符号进行解调:
| ${\hat s_k} = Q\left( {{s_k}} \right) = \mathop {\arg \min }\limits_{s \in S} \left( {{{\left| {{s_k} - s} \right|}^2}} \right) $ | (6) |
得到了假设激活天线和对应的估计符号后,通过ML检测处理得到最终的检测结果为
| $ \left(k, \hat{s}_{k}\right)=\arg \min \left\|\boldsymbol{y}-\boldsymbol{h}_{k} \hat{s}_{k}\right\|_{\mathrm{F}}^{2} $ | (7) |
通过在L组候选的天线序号和对应的星座符号中进行搜索,最终可以得到估计的激活天线序号k和天线的发送符号
下面首先分析本文算法的误码率性能,并与ML最优算法以及其他一些现有算法的性能进行比较.然后分析新算法的计算复杂度,并与一些传统算法的计算复杂度并进行比较.
3.1 性能分析为了验证新算法的性能,给出了IMMRC算法的性能分析,并与现有算法如ML算法、SVD算法、MMRC算法的性能进行比较.在仿真时,采用未编码的SM系统,假设信道为归一化准静态瑞利衰落信道,接收端已知完整信道状态信息.考虑不同的发送天线和调制方式下的误码率(BER, bit error rate)性能.
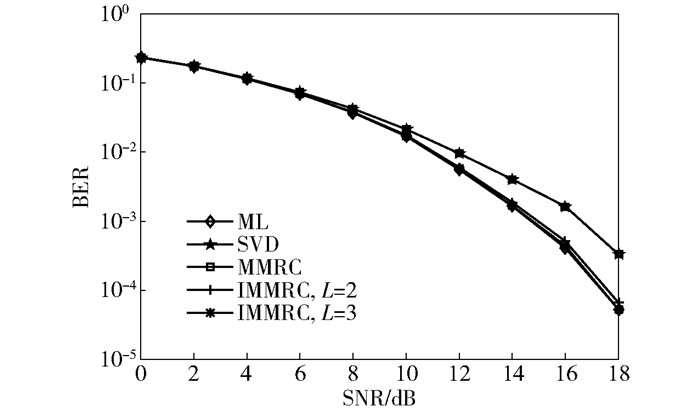
图 1所示为16根发射天线,4根接收天线的SM系统,采用QPSK调制方式,频谱效率为η=6 bit·s-1·Hz-1.仿真了ML算法、SVD算法、MMRC算法以及IMMRC算法的BER性能,其中候选集大小数L分别取2和3.可以看出,在低信噪比的情况下,几种信号检测算法的性能差异不明显,随着信噪比的增大,IMMRC算法的性能明显优于SVD算法以及MMRC算法.当BER为10-3时,与ML算法相比,IMMRC算法在L=2时有1 dB的性能损失,在L=3时仅有0.3 dB的性能损失,说明样本空间的增大可以改善算法的性能.同时,仿真结果也说明,一个小的候选序列(L=3)就可以满足近似ML的检测性能.

|
图 1 (QPSK,16×4)误码率性能 |
图 2所示为4根发射天线,4根接收天线,采用16QAM调制方式下的BER性能曲线.分别仿真了ML算法、SVD算法、MMRC算法以及IMMRC算法的BER性能,其中候选集大小数L分别取2和3.观察图 2中的仿真性能曲线可以知道,本文算法的性能优于SVD算法和MMRC算法, 接近最优ML算法的性能,也可以得出和图 1类似的结论.综合图 1和图 2,从仿真曲线可以看出,IMMRC算法的性能优于MMRC算法.随着L的增加,IMMRC算法的性能也接近于ML算法的性能,但是复杂度会稍微增加.因此,可以通过L的选择在系统性能和计算复杂度之间进行折中选择.同时,发送端的天线数较多时,样本空间的天线候选数取值对BER性能的影响较为明显.
|
图 2 (16QAM,4×4)误码率性能 |
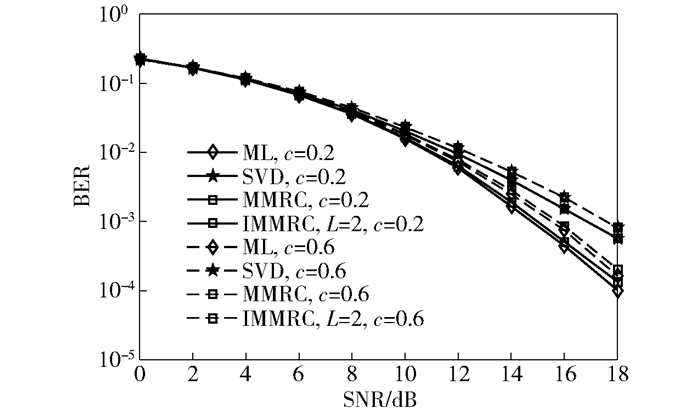
图 3所示为考虑了相关瑞利衰落信道[7]的情况.设相关衰落信道为H=HWA,矩阵A满足R=AHA,其中矩阵HW的元素hWi, j满足hWi, j~CN(0, 1),相关矩阵R里面的元素满足ri, j=c|i-j|,i, j=1, …, Nt.发送端天线数为4根,接收端天线数为4根,采用16QAM调制方式.分别仿真了ML算法、SVD算法、MMRC算法以及IMMRC算法的在相关信道下的BER性能,相关系数为0.2和0.6(c=0.2和0.6).从仿真结果可知,在相关信道下,IMMRC算法的BER性能要优于SVD算法和MMRC算法,在相关系数比较小时,BER性能要更好一点.
|
图 3 相关信道下的误码率性能 |
本节主要分析新算法和几种常见的SM系统检测算法的计算复杂度,并进行比较.假设SM系统有Nt根发送天线,有Nr根接收天线,采用M阶数字调制方式,用实数乘法的计算次数来衡量算法的计算复杂度,并且忽略一些特殊函数的计算复杂度.根据第3节的检测过程可知:计算权重因子τi=|(hiHy)/‖hi‖F|时需要的实数乘法运算次数为(6Nr+3)Nt;计算sk时需要的实数乘法运算次数为8LNr;最后进行ML搜索时需要的实数乘法运算次数为L(Nr-1),得到MMRC算法总的算法计算复杂度为(6Nr+3)Nt+8LNr+L(Nr-1).其他算法的计算复杂度可以查阅相关的文献. 表 2给出了ML算法、SVD算法、MRC算法、MMRC算法以及改进算法的计算复杂度表达式.
|
|
表 2 算法的计算复杂度 |
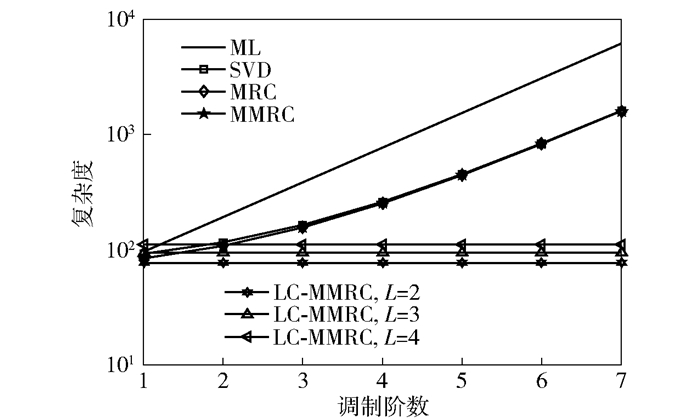
图 4所示为各种检测算法之间的复杂度.通过之前的分析,算法的复杂度与发射天线数、接收天线数及调制阶数有关.这里将发射天线和接收天线数目固定,算法复杂度可表示为调制阶数M的函数.从图 4可以看出,随着M的增长,ML算法、SVD算法、MRC算法和MMRC算法的计算复杂度也随之增长,而IMMRC算法的计算复杂度要低于它们.尤其当调制阶数较大时,计算复杂度远远低于前面几种算法.此外,IMMRC算法的复杂度与调制阶数无关,只与天线候选集的个数L有关,当L增大时,复杂度会稍微增加.在SM系统中,IMMRC算法的复杂度要远远低于ML算法,尤其是在高阶调制系统中,说明了该算法具有实际意义.
|
图 4 各种检测算法的复杂度 |
提出了一种适用于SM系统低复杂度的MMRC改进算法,算法的检测性能逼近ML算法.在检测发送天线序号时产生一个候选天线集,然后进行发送符号的检测,提出的算法可以以一个很小的候选集而达到接近最优ML检测的性能.通过改变L的值可以在算法的计算复杂度和误码率性能之间进行选择.多天线技术和绿色通信是未来无线通信的发展方向,空间调制技术作为MIMO技术的一种,是未来无线通信的备选方案之一,因此笔者提出的算法具有一定的实际应用意义.
| [1] |
申滨, 赵书锋, 黄龙杨. 基于Jacobi迭代的大规模MIMO系统低复杂度软检测算法[J]. 北京邮电大学学报, 2017, 40(5): 55-60. Shen B, Zhao S F, Huang L Y. Low complexity soft detection algorithm for large-scale MIMO systems based on Jacobi iteration[J]. Journal of Beijing University of Posts and Telecommunications, 2017, 40(5): 55-60. |
| [2] |
王增祥, 李国权, 张杰. 空间调制的天线选择和能效优化算法[J]. 中国新通信, 2017, 19(5): 53-58. Wang Z X, Li G Q, Zhang J. Spatial modulation antenna selection and energy efficiency optimization algorithm[J]. China New Communications, 2017, 19(5): 53-58. DOI:10.3969/j.issn.1673-4866.2017.05.048 |
| [3] |
Ntontin K, Renzo M D, Perez-Neira A, et al. Performance analysis of multistream spatial modulation with maximum-likelihood detection[C]//2013 IEEE Global Communications Conference(IGCC). Atlanta: IEEE Press, 2013: 1590-1594.
|
| [4] |
门宏志, 金明录. 低复杂度空间调制MPSK信号的最优检测[J]. 通信学报, 2015, 36(8): 118-124. Men H Z, Jin M L. Low-complexity optimal MPSK detection for spatial modulation[J]. Journal on Communications, 2015, 36(8): 118-124. |
| [5] |
Zhang X, Zhao G, Liu Q, et al. Enhanced M-algorithm based maximum likelihood detectors for spatial modulation[J]. International Journal of Electronics and Communications, 2016, 70(9): 1361-1366. DOI:10.1016/j.aeue.2016.06.015 |
| [6] |
Peng S, Bai Z, Su Y, et al. MRC based SER analysis of high efficient UWB spatial modulation system[C]//2017 13th International Wireless Communications and Mobile Computing Conference(IWCMC). Valencia: IEEE Press, 2017: 1712-1716.
|
| [7] |
Wang J, Jia S, Song J. Signal vector based detection scheme for spatial modulation[J]. IEEE Communications Letters, 2012, 16(1): 19-21. DOI:10.1109/LCOMM.2011.111611.112127 |
| [8] |
Lee G H, Kim T H. Implementation of near optimal detector for spatial modulation MIMO systems[J]. IEEE Transactions on Circuits and Systems Ⅱ Express Briefs, 2016, 63(10): 954-958. DOI:10.1109/TCSII.2016.2536239 |
| [9] |
Maleki M, Bahrami H R, Alizadeh A. On MRC-based detection of spatial modulation[J]. IEEE Transactions on Wireless Communications, 2016, 15(4): 3019-3029. DOI:10.1109/TWC.2016.2514421 |
| [10] |
Xiao L, Xiao Y, Xu C, et al. Compressed sensing assisted spatial multiplexing aided spatial modulation[J]. IEEE Transactions on Wireless Communications, 2017, 17(2): 794-807. |
| [11] |
Lee K. Doubly ordered sphere decoding for spatial modulation[J]. IEEE Communications Letters, 2015, 19(5): 795-798. DOI:10.1109/LCOMM.2015.2415808 |



