道路中车流量密度比较大时,会有大量车辆终端接入车辆异构无线网络,易造成网络阻塞,对此,提出结合自组织网络的自组织异构网络方法.当网络未发生阻塞时,车辆终端采用效用函数算法在基站或者接入点之间进行网络选择;当网络可能发生阻塞时,首先通过分簇算法将自组织网络划分为若干簇;然后进行车辆状态之间的转化;最后根据车辆状态选择接入算法.仿真结果表明,所提算法降低了网络发生阻塞的概率,提高了系统的吞吐量.
The combination of Ad hoc and heterogeneous network with infrastructure was proposed to alleviate network congestion. When the network was not congested, the vehicle terminal used utility function algorithm to select network between the base stations or the access points in order to complete the vertical handoff quickly. When the network was congested, firstly, the Ad hoc was divided into several clusters by clustering algorithm; then, the transition among vehicle states was carried out; finally, the access algorithm was selected according to the vehicle status. Simulation results show that the proposed algorithm reduces the probability of network congestion and improves the system throughput.
车辆异构无线网络中,车辆终端的快速移动使网络切换的次数增多.当前的垂直切换算法大致分为基于多属性决策的算法[1]、基于马尔可夫过程的算法[2]和基于模糊逻辑的算法[3].但是当用户终端数量急剧增加时,继续使用上述算法为用户终端选择接入网络,极易造成网络阻塞.
把自组织网络结合到车辆异构网络中是一个很好的策略,笔者将这种异构网络称之为自组织异构网络. Shafiee等[4]利用车与车之间(V2V, vehicle to vehicle)的通信,将接入点(AP, access point)覆盖范围之外的信息中继到AP,以避免接入蜂窝网络,缺点是没有考虑接入用户数较多情况下的性能问题. Lee等[5]利用V2V通信将数据包转发到最合适的AP,以均衡网络之间的负载,但在移动速度较快的场景中,容易暴露出链路易断的问题.
在车辆异构网络组网中,结合自组织网络来联合组网,同时将自组织网络组网形式考虑成簇结构,减少了直接接入基站(BS, base station)或AP中的用户数,降低了网络发生阻塞的可能.
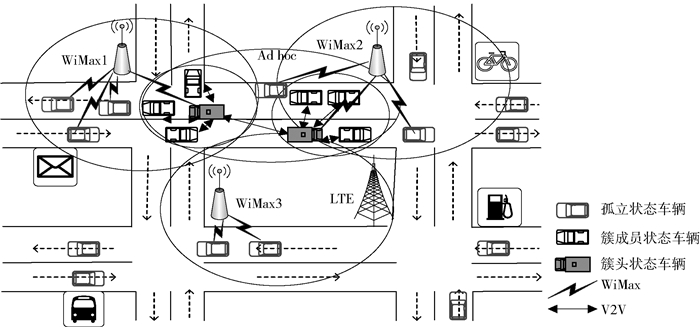
1 自组织异构网络模型网络模型如图 1所示.该模型将自组织网络的组网形式考虑成由一个簇头(CH, cluster head)和多个簇成员(CM, cluster member)节点组成的若干个簇结构.其中CH控制用户业务的接入请求,并合理地分配带宽,减少直接接入网络中的用户数.
|
图 1 自组织异构网络模型 |
假设:1)场景中每辆车都拥有唯一的ID号,且车辆无线通信范围均相同;2)每辆车都装备GPS设备;3)每辆车都有一个车辆信息库(VIB, vehicle information base),用于储存车辆自身和邻居车辆的信息;4)设置簇中CM数量的上限maxCM和下限minCM;5)将场景中的车辆设置初始状态,即孤立状态(IS, isolated status).
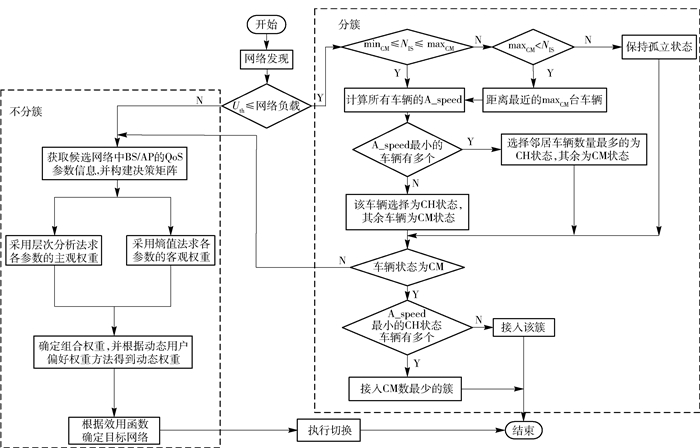
2 降低阻塞的垂直切换算法流程降低阻塞的垂直切换算法流程如图 2所示,算法可分为2个阶段:1)网络检测.车辆终端获取可用网络的负载信息;2)切换执行.当网络未发生阻塞时,采用效用函数算法进行接入网络选择.当网络可能发生阻塞时,首先,通过分簇算法将Ad hoc网络划分为若干簇结构;然后,进行车辆状态之间的转化;最后,根据车辆状态选择接入算法.
|
图 2 降低阻塞的垂直切换算法流程 |
基本流程如下:
1) 车辆之间通过Hello消息建立自身的VIB;
2) IS车辆通过媒体独立信息服务获取周围网络的负载状态,若网络负载少于网络同时最多可以容纳的用户数量阈值Uth,车辆将保持IS;否则转入3);
3) 若IS车辆的邻居车辆数量NIS少于minCM,车辆将保持IS;否则,转入4);
4) 若minCM≤NIS≤maxCM,将进行簇头选举过程;否则,转入5);
5) 若maxCM < NIS,车辆将与距离最近的maxCM台车辆进行CH的选举过程.
当切换的车辆是CH状态或者IS时,采用效用函数算法进行接入网络选择;当切换的车辆是CM状态时,接入平均相对速度最小的簇中,若平均相对速度最小的CH状态车辆有多个,则接入簇成员数最少的簇中.
3 网络组网与动态更新 3.1 簇头选举过程用Ni表示车辆i的邻居车辆数量,Vi为车辆i的速度,Vij为车辆i的第j台邻居车辆的速度. CH选举过程如下.
1) 簇在初始化时,车辆之间通过发送交互Hello消息获取其邻居车辆的信息,建立自身的VIB.
2) 计算车辆i的平均相对速度.
| $ {{\rm{A}}_ - }{\rm{spee}}{{\rm{d}}_i} = \frac{{\sum\limits_{j = 1}^{{N_i}} {\left| {{V_i} - {V_{ij}}} \right|} }}{{{N_i}}} $ | (1) |
3) 选举相邻车辆中A_speed最小的车辆作为CH状态,其他车辆皆为CM状态,若A_speed最小的车辆有多个,则将邻居车辆数量最多的车辆设为CH状态.
3.2 簇维护过程1) IS车辆加入簇.若IS车辆与CH状态车辆成为邻居,且numCM < maxCM,则比较IS和CH状态车辆的A_speed,A_speed较小的车辆为CH状态,另一车辆为CM状态.
2) 离开簇.当一个CM状态车辆离开当前簇的覆盖区域,则其状态转化为IS.
3) 簇合并.如果2个CH成为邻居,并且其CM有超过一半是重叠的,则A_speed较小的CH继续保持为CH状态,并将另一个簇内的所有成员合并到该簇中.在簇合并前,要保证合并后的numCM不能大于maxCM.
4) 簇消亡.如果numCM < minCM,CH将发送簇消亡消息,然后该簇内的所有车辆将各自当前的状态转化成IS,以减少网络中簇的数量.
5) 远离当前簇进入其他簇覆盖区域.当一个CM状态车辆进入其他簇的覆盖区域,则比较CM和CH状态车辆的A_speed,A_speed较小的车辆为CH状态,另一车辆为CM状态.
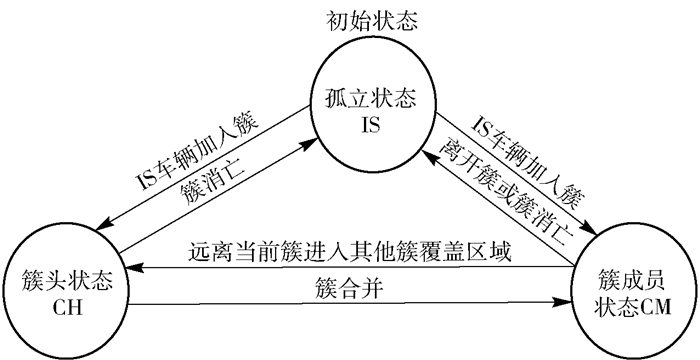
综上所述,车辆之间的状态转化如图 3所示.
|
图 3 车辆状态的转化 |
选取时延、抖动、丢包率以及带宽4个参数,假设候选网络总数为n,切换决策属性的总数为m.其中候选网络Bi(i=0, 1, …, n)属性Cj(j=1, 2, …, 4)的测量值是cij,由于异构网络中各个网络属性参数之间没有直接可比性,所以需要对属性测量值进行归一化处理.
效益型属性:
| $ {c_{ij}} = \frac{{{{\bar c}_{ij}} - \min \left( {{{\bar c}_{ij}}} \right)}}{{\max \left( {{{\bar c}_{ij}}} \right) - \min \left( {{{\bar c}_{ij}}} \right)}} $ | (2) |
成本型属性:
| $ {c_{ij}} = \frac{{\max \left( {{{\bar c}_{ij}}} \right) - {{\bar c}_{ij}}}}{{\max \left( {{{\bar c}_{ij}}} \right) - \min \left( {{{\bar c}_{ij}}} \right)}} $ | (3) |
则可构建决策矩阵为
| $ \mathit{\boldsymbol{P}} = \left[ {\begin{array}{*{20}{c}} {{c_{11}}}&{{c_{12}}}&{{c_{13}}}&{{c_{14}}}\\ {{c_{21}}}&{{c_{22}}}&{{c_{23}}}&{{c_{24}}}\\ \vdots & \vdots & \vdots & \vdots \\ {{c_{n1}}}&{{c_{n2}}}&{{c_{n3}}}&{{c_{n4}}} \end{array}} \right] $ | (4) |
1) 层次分析法计算主观权重
① 建立递阶层次结构模型.模型中最上层为目标层,中间层为准则层,最下层为不同的候选网络.
② 构造判断矩阵.根据参数对于目标层的重要程度,得到判断矩阵A=(aij)4×4,其中aij表示第i个属性与第j个属性的比较参考值,且aij=1/aji.
③ 权重向量计算.根据判断矩阵A,求出其最大特征根λmax所对应的特征向量W1,有
| $ \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{W}}_1} = {\lambda _{\max }}{\mathit{\boldsymbol{W}}_1} $ | (5) |
④ 一致性检验.判断得到的权重分配是否合理,有
| $ R = I/T $ | (6) |
其中:R为判断矩阵A的随机一致性比率,T为矩阵A的随机一致性指标,I为A的一般一致性指标.
当A的R < 0.1时,表明A的一致性程度在允许范围内;否则,对A进行调整,直到符合条件为止.
2) 熵值法计算客观权重W2=(w2j)1×4
① 对矩阵P中的每个参数值计算信息熵值:
| $ {e_j} = - k\sum\limits_{i = 1}^n {{d_{ij}}} \ln {d_{ij}},{d_{ij}} = \frac{{{c_{ij}}}}{{\sum\limits_{i = 1}^n {{c_{ij}}} }} $ | (7) |
其中:k=1/lnn,dij为第j个参数占网络i中所有参数的比重.
② 计算第j个参数的熵冗余度rj:
| $ {r_j} = 1 - {e_j} $ | (8) |
③ 求出属性参数j的权重w2j:
| $ {w_{2j}} = \frac{{{r_j}}}{{\sum\limits_{j = 1}^m {{r_j}} }} $ | (9) |
3) 计算主客观组合权重W3=(w3j)1×4
用x和y分别表示W1和W2的系数,则W3为
| $ {\mathit{\boldsymbol{W}}_3} = x{\mathit{\boldsymbol{W}}_1} + y{\mathit{\boldsymbol{W}}_2} $ | (10) |
| $ \text{suject to}:0 \le {w_{3j}} \le 1,\sum {{w_{3j}}} = 1 $ | (11) |
4) 对组合权重W3进行动态调整
设δwij为网络Bi的属性Cj的调整因子,则增益型属性的调整因子δwij为
| $ \delta {w_{ij}} = \left\{ {\begin{array}{*{20}{l}} {\left( {{c_{ij}} - c{\rm{t}}{{\rm{h}}_{ij}}} \right)/c{\rm{t}}{{\rm{h}}_{ij}},}&{若\;{c_{ij}} > c{\rm{t}}{{\rm{h}}_{ij}}}\\ {0,}\ \ \ \ \ \ {若\;{c_{ij}} \le c{\rm{t}}{{\rm{h}}_{ij}}} \end{array}} \right. $ | (12) |
成本型属性的调整因子δwij为
| $ \delta {w_{ij}} = \left\{ {\begin{array}{*{20}{l}} {\left( {c{\text{th}_{ij}} - {c_{ij}}} \right)/c{\text{th}_{ij}}}&{若\;{c_{ij}} < c{\rm{t}}{{\rm{h}}_{ij}}}\\ {0,}\ \ \ \ \ \ {若\;{c_{ij}} \ge c{\rm{t}}{{\rm{h}}_{ij}}} \end{array}} \right. $ | (13) |
其中:δwij∈[0, 1], cthij代表网络i属性j的阈值.
动态权重调整公式为
| $ {w_{4j}} = {w_{3j}}\delta {w_{ij}} $ | (14) |
则参数的最终权重向量W4=(w4j)1×4.
4.3 基于效用函数选择最优网络4.1和4.2节详细介绍了属性参数的归一化和每个参数权重的确定方法,效用函数计算公式为
| $ \mathit{\boldsymbol{O}} = \mathit{\boldsymbol{PW}}_4^{\rm{T}} $ | (15) |
孤立CH或者CH车辆终端将会接入到O中最大元素所对应的网络.
5 实验结果和分析使用Matlab对所提出的切换算法进行仿真.仿真场景如图 1所示,场景中,LTE实现全覆盖,WiMax和Ad hoc的覆盖半径分别为1 km和300 m. LTE和WiMax的带宽分别为20 MHz和15 MHz,而Ad hoc的带宽为5 MHz.在整个网络覆盖区域按照泊松分布陆续到达新用户,到达率为0≤λ≤1(个/s),服务时间的均值为60 s.
将所提的算法与基于移动趋势量化的多属性算法[1](M-MTQ, multi-attribute handoff algorithm motion trend quantification)以及增强型的模糊逻辑算法[3](E-FMADM, enhanced fuzzy MADM)进行比较分析.
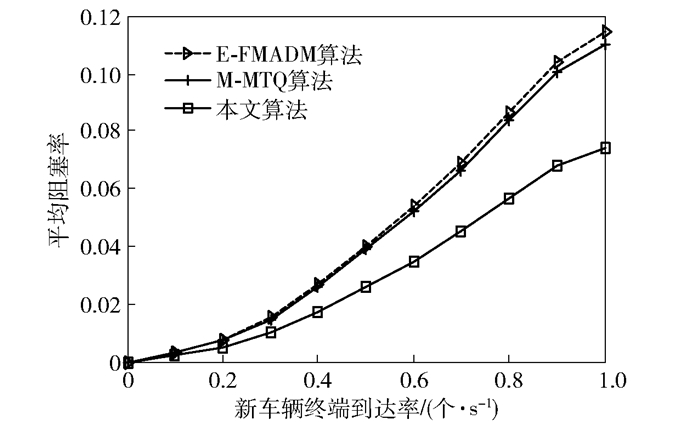
5.1 阻塞率分析图 4为3种算法的平均阻塞率曲线.可以看出,在0≤λ < 0.1(个/s)时,由于无线网络的容量能够保证新车辆终端的接入,所以车辆终端的平均阻塞率等于零或者几乎接近于零.当0.1≤λ≤1(个/s)时,随着车辆终端到达率的增加,3种算法的平均阻塞率也随之增加,但是,在相同车辆终端到达率的情况下,本文算法的阻塞率始终低于其他2种算法.这是因为当车辆终端数量增多时,通过引入自组织网络,减少了直接接入BS或者AP中的车辆终端数量,从而有效降低了车辆终端的平均阻塞率.
|
图 4 车辆终端平均阻塞率 |
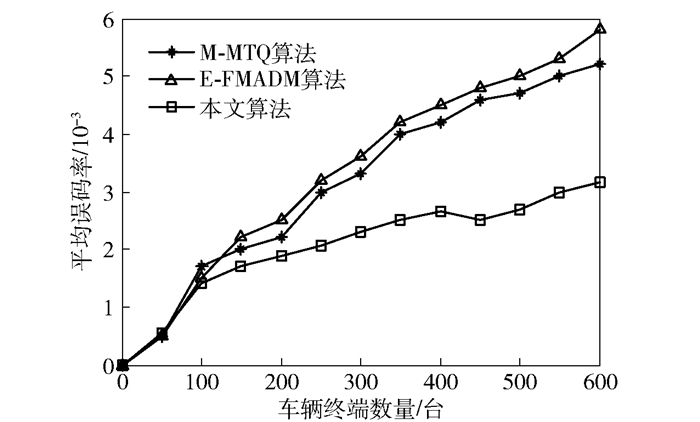
图 5为3种算法的网络平均误码率随车辆终端数量的变化曲线.可以看出,在车辆终端数量少于50台时,3种算法的平均误码率相差不大,但是,随着车辆终端数量的增多,其他2种算法的平均误码率增加得特别迅速,而本文算法的误码率增加较缓慢.但在同样车辆终端数量下,本文算法的平均误码率比其他2种算法低,这是由于本文算法中引入自组织网络,所以当车辆终端数量增多时,车辆之间直接进行通信,减少了接入网络中的车辆终端数量,降低了网络阻塞引起的误码.
|
图 5 网络平均误码率 |
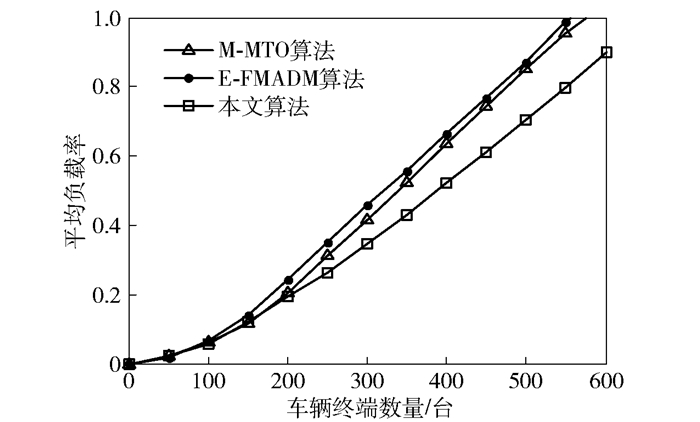
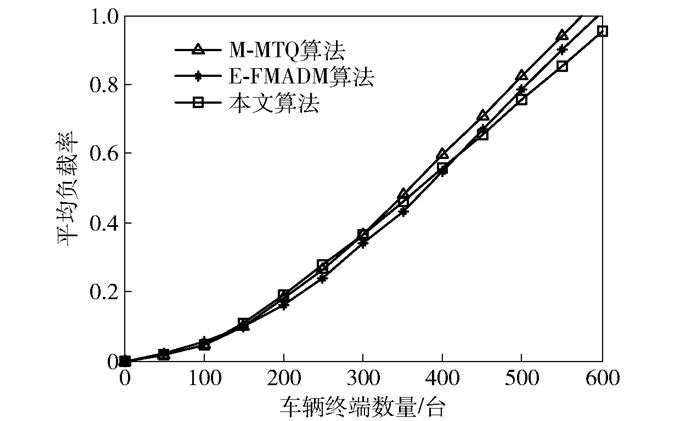
图 6和图 7为3种算法的平均负载率与车辆终端数量的关系.可以看出,随着车辆终端数量的增多,M-MTQ和E-FMADM两个算法的负载率迅速增加直至满载. 图 6中,本文算法的负载率始终低于其他2种算法的负载率,而图 7中,当车辆终端数量大于400台时,本文算法的负载率比其他2种算法的负载率低.这是因为当车辆终端数量增多时,本文算法将进行分簇过程,减少直接接入网络的车辆终端数量,因此,网络的负载率更低.
|
图 6 LTE无线网络平均负载率 |
|
图 7 WiMAX无线网络平均负载率 |
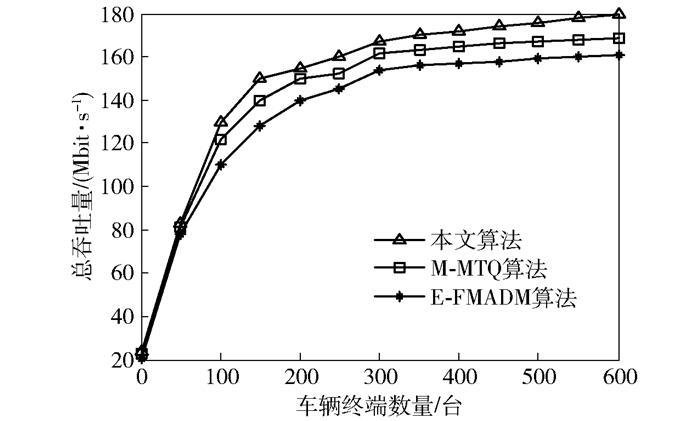
图 8为3种算法的吞吐量随着车辆终端数量的变化曲线.当车辆终端数量少于400台时,3种算法的吞吐量随车辆终端数量的增加而迅速增大;而当车辆终端数量大于400台时,3种算法的吞吐量的增加比较缓慢.此外,在相同车辆终端数量的情况下,本文算法的吞吐量始终高于其他2种算法,这是由于本文算法通过引入自组织网络减少了接入基础设施的车辆终端数量,使本文算法的网络资源利用率更高,从而有效提高了系统吞吐量.
|
图 8 网络总吞吐量 |
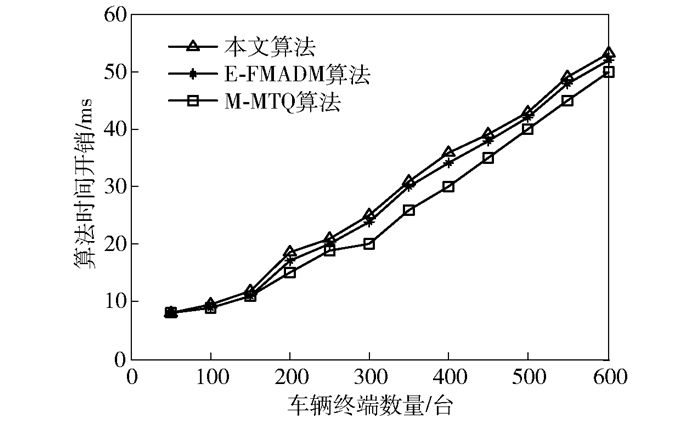
图 9所示为3种算法时间开销的对比.可以看出,在车辆终端数量比较少时,3种算法的时间复杂度相差不大,但随着车辆终端数量的增多,由于本文算法需要进行分簇以及簇的维护等,算法的时间复杂度比其他2种算法的时间复杂度稍微大些.
|
图 9 算法时间开销 |
为解决车辆异构网络中,当道路中车流量比较大时,可能造成网络阻塞的问题,提出在车辆异构网络中引入自组织网络,同时把自组织网络的组网形式考虑成簇结构,减少直接接入到BS或者AP的终端数量.仿真结果表明,该算法降低了网络平均误码率,提高了系统的吞吐量,有效保证了车辆终端的服务质量.
| [1] |
潘甦, 梁宇, 刘胜美. 一种基于移动趋势量化的多属性垂直切换判决算法[J]. 电子与信息学报, 2016, 38(2): 269-275. Pan Su, Liang Yu, Liu Shengmei. A multi attribute vertical handoff decision algorithm based on motion trend quantification[J]. Journal of Electronics and Information Technology, 2016, 38(2): 269-275. |
| [2] |
马彬, 谢显中, 廖晓峰. 车辆异构网络中预测垂直切换算法[J]. 电子与信息学报, 2015, 37(4): 874-880. Ma Bin, Xie Xianzhong, Liao Xiaofeng. Prediction vertical handoff algorithm in vehicle heterogeneous network[J]. Journal of Electronics and Information Technology, 2015, 37(4): 874-880. |
| [3] |
Zineb A B, Ayadi M, Tabbane S. An enhanced vertical handover based on fuzzy inference madm approach for heterogeneous networks[J]. Arabian Journal for Science and Engineering, 2017, 42(8): 3263-3274. DOI:10.1007/s13369-017-2418-1 |
| [4] |
Shafiee K, Attar A, Leung V C M. Optimal distributed vertical handoff strategies in vehicular heterogeneous networks[J]. IEEE Journal on Selected Areas in Communications, 2011, 29(3): 534-544. DOI:10.1109/JSAC.2011.110304 |
| [5] |
Lee S, Sriram K, Kim K, et al. Vertical handoff decision algorithms for providing optimized performance in heterogeneous wireless networks[J]. IEEE Transactions on Vehicular Technology, 2009, 58(2): 865-881. DOI:10.1109/TVT.2008.925301 |



