保护隐私的交集计算(PSI, private sets intersec-tion)作为一种特殊的隐私保护的计算方法，已经成为安全多方计算的重要研究方向之一^[1].但是随着云计算应用的兴起，越来越多的用户希望委托云平台来完成私有信息的存储和交集计算工作，但云不能完全被信任.而不良行为势必会给用户私有数据集的存储和计算带来新的挑战. Abadi等^[2]提出了利用同态加密和多项式插值实现的两方交集协议，该协议采用Kissner等^[3]提出的数学原理进行集合交集计算，允许多个客户端用户求集合交集.在此工作基础上，Abadi等^[4]又提出了可验证的云外包PSI协议，既保证客户端用户输入数据的隐私性又可保证输入数据的完整性.上述2个方案解决了隐私数据的完全委托问题，而且也不需要进行本地副本的维护，但在交集计算过程中参与双方有交互.李顺东等^[5]利用哥德尔编码和ELGamal同态加密算法构造了一种半诚实模型下适用于云计算的集合交集计算方案.该方案解决了多个集合间的交集并集问题，但不能解决2个集合间的交集问题.

利用集合的多项式模型构造出一种基于云外包的安全两方集合交集计算协议.用户能够直接将自己的隐私数据存独立存储在云端，并且用户在委托云平台进行存储和计算时，不会泄露自己的隐私信息.计算成本进行分析表明协议的计算开销优于文献[2, 4].

1 预备知识 1.1 Boneh算法

Boneh等^[6]提出的一种同态加密方案如下：

密钥产生：Alice选取N=pq，其中p, q为素数，对于双线性对e:(G₁×G₁→G)，G₁, G为阶数为N的群，g, u为G₁的2个随机生成元，且h=u^p. Alice生成公私钥对：(PK, SK)=((G₁, G, e, g, h, N), q).

加密过程：明文m < p，任取随机数r∈Z_N，密文c=g^mh^r.

解密过程：对于密文c < N，利用私钥sk=q₁计算$c^{q_{1}}=\left(g^{m} h^{r}\right)^{q_{1}}=(\hat{g})^{m}$，其中$ \hat{g}=g^{q_{1}} $.然后通过计算c^q₁的离散对数恢复明文m.

假设E为一个加密算法，C₁=E(m₁, r₁)，C₂=E(m₂, r₂)分别是对消息m₁，m₂的加密，r₁, r₂是随机数，则有以下公式成立：

$ E\left( {{m_1}} \right)E\left( {{m_2}} \right) = E\left( {{m_1} + m,r} \right) $

$ e\left( {E\left( {{m_1}} \right),E\left( {{m_2}} \right)} \right) = {g^{{m_1}{m_2}}}h_1^{r'} $

其中：r=r₁+r₂，r′=m₂r₁+m₁r₂+αpr₁r₂，h=g^αp，α为一个未知整数，可见，Boneh加密算法具有加法同态性和一次乘法同态性.

1.2 集合的多项式表示

1) 集合的点值多项式表示^[2]

一个阶为d的多项式ρ可以表示成n个点值对的集合{(x₀, y₀), (x₁, y₁), …, (x_n－1, y_n－1)}，其中所有的x_i都不同且有y_i=f(x_i), 0≤i≤n－1.如果x的值固定，则多项式可以用Y={y₀, y₁, …, y_n－1}表示.在点值形式下的多项式可以通过多项式插值转化为系数形式.而对应的多项式计算也可以被逐点相加或相乘完成.假设2个阶数为d的多项式ρ_A(x)ρ_B(x)，对应点值形式的向量分别为y^(A), y^(B)，那么

$ \begin{array}{*{20}{c}} {{\rho _{\rm{A}}}(x) + {\rho _{\rm{B}}}(x) = }\\ {\left( {y_1^{({\rm{A}})} + y_1^{({\rm{B}})},y_2^{({\rm{A}})} + y_2^{({\rm{B}})}, \cdots ,y_{n - 1}^{({\rm{A}})} + y_{n - 1}^{({\rm{B}})}} \right)} \end{array} $

$ \begin{array}{*{20}{c}} {{\rho _{\rm{A}}}(x){\rho _{\rm{B}}}(x) = }\\ {\left( {y_1^{({\rm{A}})}y_1^{({\rm{B}})},y_2^{({\rm{A}})}y_2^{({\rm{B}})}, \cdots ,y_{n - 1}^{({\rm{A}})}y_{n - 1}^{({\rm{B}})}} \right)} \end{array} $

2) 集合交集的多项式模型^[7]

如果将2个元素个数相等的集合S_A、S_B各自的多项式表示分别为ρ_A(x)ρ_B(x), 那么两集合交集S_A∩S_B的多项式就可以表示为γ_Aρ_A+γ_Bρ_B.其中r, s∈R^deg(f)[x]，R^b[x]为能够独立选择系数的阶数为0, …, b的多项式集合.

引理1  假设ρ_A、ρ_B为R[x]上的2个多项式，其中R[x]是概率不可区分的多项式环，且有deg(γ_A)=deg(γ_B)=α，β≥α，gcd(γ_A，γ_B)=1.若$ u=\gamma_{\mathrm{A}} \rho_{\mathrm{A}}+\gamma_{\mathrm{B}} \rho_{\mathrm{B}}=\sum\limits_{i=0}^{\alpha+\beta} u[i] x^{i} $，那么u在R上是均匀分布并且独立的.其中$\gamma_{\mathrm{A}}=\sum\limits_{i=0}^{\beta} \gamma_{\mathrm{A}}[i] x^{i} \gamma_{\mathrm{B}}=\sum\limits_{i=0}^{\beta} \gamma_{\mathrm{B}}[i] x^{i} $，其中γ_A[i], γ_B[i]∈R, 0≤i≤β.

由引理1可知，γ_Aρ_A+γ_Bρ_B=u·gcd(ρ_A, ρ_B)成立, 其中u为均匀随机多项式.

定理1  假设TTP1、TTP2为可信第三方. TTP1接收第i个参与者的私有输入集合S_i，|S_i|=k，1≤i≤n，然后返回集合交集S₁∩…∩S_n；假设TTP2为接收第i个参与者的私有输入集合S_i，|S_i|=k，1≤i≤n，然后计算每个集合S_i对应的多项式ρ_i，选择γ_i∈R^k[x]，计算$ \sum\limits_{i=1}^{n} \gamma_{i} \rho_{i} $，并将结果返回给参与者.那么对于每个参与者，存在一个转换算法使得以下2个结果是计算不可区分的：1)将转换算法应用到TTP1的输出；2)直接返回TTP2的结果.

如果ρ_A(x)ρ_B(x)为集合S_A、S_B的多项式表示，那么根据定理2可知：γ_Aρ_A+γ_Bρ_B只能够包含2个集合交集信息，并且不含2个集合中其他元素的信息，这就构成了新PSI协议的基本模型.

2 安全多方集合交集协议 2.1 方案描述

假设Alice和Bob分别拥有各自的保密数据集合S_A={s₀^(A), s₁^(A), …, s_n－1^(A)}，S_B={s₀^(B), s₁^(B), …, s_n－1^(B)}.双方希望将自己的保密数据上传至云服务器，并且在不泄露自己隐私数据的情况下，利用外包云服务器进行隐私存储并计算两集合交集，减少用户本身的计算量.

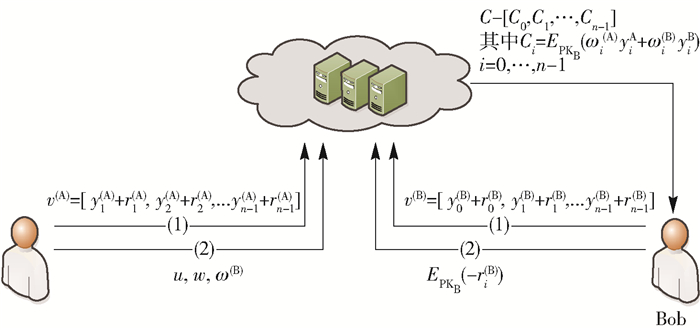
为了解决此问题，协议首先将Alice和Bob的集合表示成对应的点值形式的多项式，那么初始的保密集合就被转换成了向量.协议工作流程如图 1所示.

每个参与者首先外包各自的集合给服务器.为了实现这项工作，参与者将集合转化成向量的形式发送.因为发送给服务器的向量是盲化的，所以服务器不能计算出参与者的集合，并且其他参与者也不能够计算出交集之外的其他元素.当双方需要计算交集是，Alice和Bob分别向服务器上传计算需要的其他参数，然后由服务器根据所得信息以密文的形式计算集合交集，然后将结果发送给Bob.最后用户Bob得到一个能够被解密的加密向量，并且使用解密的值来完成一个插值多项式.

2.2 具体协议

输入：Alice输入S_A={s₀^(A), s₁^(A), …, s_n－1^(A)}

Bob输入S_B={s₀^(B), s₁^(B), …, s_n－1^(B)}

输出：f_∩(S_A, S_B)

步骤1  Server-side

服务器发布一个向量X，包括n=2d+1个取自R的不同的值.发布一个伪随机函数：f:{0, 1}^l×Z→R，该函数能够将一个L bit的字符串映射到一个R上的伪随机元素.

步骤2  Data outsource

1) Bob产生Boneh加密对(PK_B, SK_B)并且发布公钥.密钥根据Boneh给定的安全参数产生.

2) 用户I构造多项式τ_I(x)=π_s^(I)i∈S(x－s_i^(I))表示对应的集合S_I, 其中I∈{Alice，Bob}.根据服务器发布X的每个元组x_i值计算τ_I(x_i)=y_i^(I), 0≤i≤n－1.

3) 发送v^(I), I∈{Alice，Bob}给服务器.其中v_i^(I)∈v^(I)，v_i^(I)=y_i^(I)+r_i^(I)，y_i^(I)是y^(I)的元素，r_i^(I)=f(k_I, i).

步骤3  Set intersection

1) Alice从R[x]选择2个阶为d的多项式ω_I，并且计算2个向量ω^(A)和ω^(B)，其中ω_i^(I)=ω_I(x_i)，I∈{Alice，Bob}，x_i, 0≤i≤n－1是公开向量X的第i个元素.

2) Alice计算u_i=ω_i^(A)－r_i^(A)+a_i, i=0, …, n-1，w_i=ω_i^(A)r_i^(A)－(r_i^(A)－a_i)v_i^(A), i=0, …, n-1，其中a_i为随机数，并将u_i、w_i、ω_i^(B)发送给服务器.

3) Bob利用自己的公钥加密计算E_PKB(－r_i^(B))发送给服务器.其中r_i^(B)=f(k_I, i).

4) 服务器接受Alice和Bob的消息后，计算向量C的结果如下：

$ C_i^{({\rm{A}})} = e\left( {{E_{{\rm{P}}{{\rm{K}}_{\rm{B}}}}}\left( {{u_i}} \right),{E_{{\rm{P}}{{\rm{K}}_{\rm{B}}}}}\left( {v_i^{({\rm{A}})}} \right)} \right){E_{{\rm{P}}{{\rm{K}}_{\rm{B}}}}}\left( { - {w_i}} \right) $

$ C_i^{\prime ({\rm{B}})} = {E_{{\rm{P}}{{\rm{K}}_{\rm{B}}}}}\left( {\omega _i^{({\rm{B}})}} \right){E_{{\rm{P}}{{\rm{K}}_{\rm{B}}}}}\left( { - r_i^{({\rm{B}})}} \right) = {E_{{\rm{P}}{{\rm{K}}_{\rm{B}}}}}\left( {\omega _i^{({\rm{B}})} - r_i^{({\rm{B}})}} \right) $

$ \begin{array}{l} C_{i1}^{({\rm{B}})} = e\left( {{E_{{\rm{P}}{{\rm{K}}_{\rm{B}}}}}\left( { - r_i^{({\rm{B}})}} \right),{E_{{\rm{P}}{{\rm{K}}_{\rm{B}}}}}\left( { - v_i^{({\rm{B}})}} \right){E_{{\rm{P}}{{\rm{K}}_{\rm{B}}}}}\left( {\omega _i^{({\rm{B}})}} \right)} \right) = \\ \;\;\;\;\;\;\;\;{E_{{\rm{P}}{{\rm{K}}_{\rm{B}}}}}\left( { - r\left( {\omega _i^{({\rm{B}})} - y_i^{({\rm{B}})} - r_i^{({\rm{B}})}} \right)} \right) \end{array} $

$ \begin{array}{l} C_{i2}^{({\rm{B}})} = e\left( {{E_{{\rm{P}}{{\rm{K}}_{\rm{B}}}}}\left( {{i^{({\rm{B}})}}} \right),{E_{{\rm{P}}{{\rm{K}}_{\rm{B}}}}}\left( {v_i^{({\rm{B}})}} \right)} \right) = \\ \;\;\;\;\;\;\;\;{E_{{\rm{P}}{{\rm{K}}_{\rm{B}}}}}\left( {\omega _i^{({\rm{B}})}y_i^{({\rm{B}})} + \omega _i^{({\rm{B}})}r_i^{({\rm{B}})} - r_i^{({\rm{B}})}y_i^{({\rm{B}})} - r_i^{({\rm{B}})}r_i^{({\rm{B}})}} \right) \end{array} $

$ {C_i} = C_i^{({\rm{A}})}C_{i1}^{({\rm{B}})}C_{i2}^{({\rm{B}})} = {E_{{\rm{P}}{{\rm{K}}_{\rm{B}}}}}\left( {\omega _i^{({\rm{A}})}y_i^{\rm{A}} + \omega _i^{({\rm{B}})}y_i^{\rm{B}}} \right) $

并将结果C_i(i=0, 1, …, n-1)发送给Bob.

5) 收到C_i后，用户Bob解密计算向量Z.对于0≤i≤n-1有z_i=D_SKB(C_i)=ω_i^(A)y_i^A+ω_i^(B)y_i^B然后利用点值(x_i, z_i)，通过插值得到多项式ξ的系数形式，即$ \xi = {\omega ^{({\rm{A}})}}{y^{\rm{A}}} + {\omega ^{({\rm{B}})}}y_i^{\rm{B}} = \sum\limits_{j = 0}^{\alpha + \beta } u [i]{x^j} $.此多项式的根就是所求交集元素.

注释1：在开始步骤中，服务器需要发布一个有2d+1元素的向量X，因为在步骤3的5)中的多项式ξ的阶数为2d并且至少需要2d+1个插值点.在R中随机选取X中的元素以至于x_i用于多项式根的可能性可以被忽略.

注释2：步骤2 3)是用户对向量的盲化.如果用户I不盲化，而在服务器上直接存储y^(I)，那么服务器能够利用y^(I)和X通过插值计算构造出用户的多项式，这样就会泄露用户的私有集合.因此用户I随机选取r_i^(I)=f(k_I, i)利用加法计算实现对y^(I)的盲化，即v_i^(I)=y_i^(I)+r_i^(I).由于服务器不知道r_i^(I)，因而在向量盲化后，用户的私有数据得到保护.

注释3：为了计算集合交集，双方用户添加的盲化因子r_i^(I)必须被去掉.在步骤3的2)中，Alice计算u_i，w_i并发送给服务器.服务器无法得到方程S的解.

$ S:\left\{ {\begin{array}{*{20}{l}} {{w_i} = \omega _i^{({\rm{A}})}r_i^{({\rm{A}})} - \left( {r_i^{({\rm{A}})} - {a_i}} \right)v_i^{({\rm{A}})}}\\ {{u_i} = \omega _i^{({\rm{A}})} - r_i^{({\rm{A}})} + {a_i}} \end{array},0 \le i \le n - 1} \right. $

而在步骤3的3)中，Bob计算E_PKB(－r_i^(B))，服务器得不到Bob的任何信息.这2个步骤的结合使得步骤3 4)中去盲成为可能.

注释4：用户初始盲化数据集合在服务器中没有改变.事实上在步骤3的4)中，服务器始终利用用户的盲化数据副本v_i^(I)进行计算，其中I∈{Alice，Bob}.

3 方案性能分析 3.1 正确性分析

定理2  半诚实模型下，该协议能够正确计算两方集合交集.

证明  根据定理2可知，计算两集合交集向量等价于构造公式γ_Aρ_A+γ_Bρ_B.在步骤1中，服务器首先发布用于产生r_i^(I)的伪随机函数f，而且要选择X用于计算协议所需向量，因此步骤1是正确的.步骤2中，参与者Alice和Bob要根据X计算各自己集合对应的多项式向量τ_I，其中τ_I(x_i)=y_i^(I)，然后对其进行盲化得到v_i^(I)=y_i+r_i^(I)，并传送给服务器.由于r_i^(I)是由服务器在步骤1中产生的，所以步骤2是正确的.步骤3是协议的核心.其中Alice在步骤3的1)中根据X产生向量ω^(I)，I∈{Alice，Bob}，3b中Alice计算u_i，w_i发送给服务器，服务器不能得到Alice的隐私信息(见注释3)，因此步骤3的1)和2)是正确的.因为Bob利用Boneh算法计算得到E_PKB(－r_i^(B))，显然，步骤3的3)是正确的；步骤3的4)中，服务器利用Boneh算法的加法和乘法同态性完成C_i的计算.事实上，

$ \begin{array}{*{20}{c}} {C_i^{({\rm{A}})} = e\left( {{E_{{\rm{P}}{{\rm{K}}_{\rm{B}}}}}\left( {{u_i}} \right),{E_{{\rm{P}}{{\rm{K}}_{\rm{B}}}}}\left( {v_i^{({\rm{A}})}} \right)} \right){E_{{\rm{P}}{{\rm{K}}_{\rm{B}}}}}\left( { - {w_i}} \right) = }\\ {{E_{{\rm{P}}{{\rm{K}}_B}}}\left( {\omega _i^{({\rm{A}})}y_i^{({\rm{A}})}} \right)C_{i1}^{({\rm{B}})}C_{i2}^{({\rm{B}})} = {E_{{\rm{P}}{{\rm{K}}_{\rm{B}}}}}\left( {\omega _i^{({\rm{B}})}y_i^{({\rm{B}})}} \right)} \end{array} $

$ {C_i} = C_i^{({\rm{A}})}C_{i1}^{({\rm{B}})}C_{i2}^{({\rm{B}})} = {E_{{\rm{P}}{{\rm{K}}_{\rm{B}}}}}\left( {\omega _i^{({\rm{A}})}y_i^{\rm{A}} + \omega _i^{({\rm{B}})}y_i^{\rm{B}}} \right) $

而且服务器是以密文形式完成计算，不能得到Alice和Bob的任何信息，因此是正确的.最后，Bob利用私钥解密C_i，完成向量插值得到交集，显然步骤3的5)是正确的.

综上，在半诚实模型下，该协议能够正确计算两方集合交集.

3.2 安全性分析

定理3  在半诚实模型下，协议是安全的.

证明  在半诚实模型中无论协议的一方如何计算，只能得到输入和输出，那么协议是安全的.

在协议的执行过程中，如果没有关于Alice的私有信息被泄露给Bob，那么该过程称为Alice-Privacy.即存在多项式时间算法Sim_B，能够模拟现实中B*的View，使得B*无法区别他是与Alice进行合作还是与Sim_B进行合作计算.

1) 当Bob腐败时，Sim_B应答过程描述如下：Sim_B建立表T=(q, h)应答H问询. Sim_B用$ h=E_{\mathrm{PK}_{\mathrm{B}}}(\hat{y}+\hat{r}) $响应查询$ q=\hat{y} $，并将结果(q, h)记录在T中. Sim_B利用T多次响应来自用户A*的问询q. Sim_B在接收real环境下B*的信息B={v_i^(B), E_PKB(-r_i^(B)(x_i))}后，计算C_i并发送给B*.

根据构造，B*与Sim_B合作计算时得到的View为

$ \begin{array}{*{20}{c}} {{D_1} = \left\{ {v_i^{({\rm{B}})},{E_{{\rm{P}}{{\rm{K}}_{\rm{B}}}}}\left( { - r_i^{({\rm{B}})}\left( {{x_i}} \right)} \right),} \right.}\\ {\left. {{E_{{\rm{P}}{{\rm{K}}_{\rm{B}}}}}\left( {\omega _i^{({\rm{A}})}{{\hat y}^{({\rm{A}})}} + \omega _i^{({\rm{B}})}y_i^{\rm{B}}} \right)} \right\}} \end{array} $

B*与Alice合作计算时的view为

$ \begin{array}{*{20}{c}} {{D_0} = \left\{ {v_i^{({\rm{B}})},{E_{{\rm{P}}{{\rm{K}}_{\rm{B}}}}}\left( { - r_i^{({\rm{B}})}\left( {{x_i}} \right)} \right),} \right.}\\ {\left. {{E_{{\rm{P}}{{\rm{K}}_{\rm{B}}}}}\left( {\omega _i^{({\rm{A}})}y_i^{\rm{A}} + \omega _i^{({\rm{B}})}y_i^{\rm{B}}} \right)} \right\}} \end{array} $

可以看出，两者的不同之处在于元素的选取.

假设区分器$\mathscr{D} $是一种能够区分真实环境和模拟环境的算法，当输入元素D₀时，该分布算法输出结果为0；当输入元素D₁时，该分布算法输出1.且$ \mathscr{D} $可以选择集合A、B中的元素.算法$ \mathscr{D} $的不可区分性可以规约为Boneh加密算法是语义安全的.

在Boneh假设下构造模拟器Sim，该模拟器能够与$ \mathscr{D} $的交互如下：Sim用E(v_i)回答来自$ \mathscr{D} $的询问，并将(v_i=y_i+r_i, E(v_i))存入表T_H中.

不失一般性，令$ E(v)=g^{v} x^{r} \in \mathbb{G} $. Sim根据E(v)计算出C_i^(b)，并构造，选择$ b \stackrel{R}{\leftarrow}\{0, 1\} $，

$ {D_{\rm{b}}} = \left\{ {v,{E_{{\rm{P}}{{\rm{K}}_{\rm{B}}}}}( - r),{E_{{\rm{P}}{{\rm{K}}_{\rm{B}}}}}\left( {\omega _i^{({\rm{A}})}y + \omega _i^{({\rm{B}})}y_i^{({\rm{B}})}} \right)} \right\} $

$ \mathscr{D} $输出它的猜测${b^\prime }\mathop \leftarrow \limits^R \{ 0, 1\} $.如果b′=b，Sim输出1，否则输出0.

事实上，根据Boneh加密算法可知$ x \rightarrow \mathbb{G} $是均匀分布的，显然有$E(v) \rightarrow \mathbb{G} $均匀分布，因此有C_i^(b)均匀分布，且独立于b.在这种情况下，Pr[b=b′]=1/2.因此，$ \mathscr{D} $是计算不可区分的.即B*无法区别他是与Alice进行合作还是与Sim_B进行合作计算.

2) 当Bob和服务器腐败时，构造Sim_B如下：Sim_B建立表T=(q, h)应答H问询. Sim_B用$ h=\hat{v}=\hat{y}+\hat{r} $响应查询$ q=\hat{y} $，并将结果(q, h)记录在T中. Sim_B利用T多次响应来自用户B*的问询q. Sim_B在接收real环境下B*的信息B={v_i^(B), E_PKB(-r_i^(B)(x_i))}后，计算C_i.

通过构造，B*与Sim_B合作计算时得到的View为

$ {D_1} = \left\{ {\begin{array}{*{20}{l}} {{{\hat v}_i},{u_i},{w_i},\mathit{\omega }_i^{({\rm{B}})},}\\ {v_i^{({\rm{B}})},{E_{{\rm{P}}{{\rm{K}}_{\rm{B}}}}}\left( { - r_i^{({\rm{B}})}\left( {{x_i}} \right)} \right),{E_{{\rm{P}}{{\rm{K}}_{\rm{B}}}}}\left( {\omega _i^{({\rm{A}})}\hat y + \omega _i^{({\rm{B}})}y_i^{\rm{B}}} \right)} \end{array}} \right\} $

B*与Alice合作计算时的view为

$ \begin{array}{*{20}{c}} {{D_0} = }\\ {\left\{ {\begin{array}{*{20}{l}} {v_i^{({\rm{A}})},{u_i},{w_i},\omega _i^{({\rm{B}})},}\\ {v_i^{({\rm{B}})},{E_{{\rm{P}}{{\rm{K}}_{\rm{B}}}}}\left( { - r_i^{({\rm{B}})}\left( {{x_i}} \right)} \right),{E_{{\rm{P}}{{\rm{K}}_{\rm{B}}}}}\left( {\omega _i^{(\text{A} )}y_i^{\rm{A}} + \omega _i^{({\rm{B}})}y_i^{\rm{B}}} \right)} \end{array}} \right\}} \end{array} $

可以看出两者的不同之处在于元素选取.

同样，假设区分器$ \mathscr{D} $是一种能够区分真实环境和模拟环境的算法.其中

$ \mathscr{D} = \left\{ {\begin{array}{*{20}{l}} {1,}&{D = {D_1}}\\ {0,}&{D = {D_0}} \end{array}} \right. $

构造能与$ \mathscr{D} $进行交互的模拟器Sim，利用回答问询计算E_PKB(ω_i^(A)y+ω_i^(B)y_i^B)，选择$b \stackrel{R}{\leftarrow}\{0, 1\} $构造

$ \begin{array}{*{20}{c}} {{D_b} = }\\ {\left\{ {\begin{array}{*{20}{c}} {v,{u_i},{w_i},\omega _i^{({\rm{B}})},}\\ {v_i^{({\rm{B}})},{E_{{\rm{P}}{{\rm{K}}_{\rm{B}}}}}\left( { - r_i^{({\rm{B}})}\left( {{x_i}} \right)} \right),{E_{{\rm{P}}{{\rm{K}}_{\rm{B}}}}}\left( {\omega _i^{({\rm{A}})}y_i^{\rm{A}} + \omega _i^{({\rm{B}})}y_i^{\rm{B}}} \right)} \end{array}} \right\}} \end{array} $

$ \mathscr{D} $输出它的猜测$ b^{\prime} \stackrel{R}{\leftarrow}\{0, 1\} $.如果b′=b，Sim输出1，否则输出0.

根据Boneh加密算法可知，Pr[b=b′]=1/2，即$ \mathscr{D} $是计算不可区分的.

由1) 2)可知，在协议执行过程中，Bob没有得到Alice的任何私有信息.

类似地，可以证明Bob-Privacy.

综上，半诚实模型下，协议是安全的.

3.3 性能分析

1) 计算复杂度.由于协议采用Boneh同态加密算法，协议的整体计算成本由模加法运算，模乘运算和模幂运算决定.因此，将这3种运算的数量作为衡量协议计算复杂度的指标.用户Alice执行了4n模加运算和2n次模乘运算.用户Bob执行n次模加运算和2n次模幂运算.服务器端执行了4n次模乘运算和3n次模幂运算.因此，协议的整体运算开销为5n次模加运算、6n次模乘运算和5n次模幂运算.

2) 通信复杂度.在多方保密计算研究中通常使用通信轮数(Round)作为衡量通信复杂度的指标.协议中用户Bob的通信轮次为1 Round.云服务器和Bob之间的通信轮次为1 Round，因此协议总的通信轮次为3 Round，而用户之间没有交互.需要说明的是，总的通信轮次是根据协议实施过程进行计算的，即只考虑各参与方有没有进行过程参数的传递，并没有考虑Bob将最终计算结果发送给Alice这一交互过程.

3) 开销比较.由于不同协议采用的同态算法不同，文献[2, 4]采用Paillier同态算法，该算法模幂运算的模数p²p²，而新方案采用Boneh同态算法，其模幂运算的模数为pq.又由于方案的N值也不同，新方案和文献[2]方案中的n值为2d+1，而文献[4]方案中n=2d+3.为方便比较本文假设新方案的模幂运算为M₁，文献[2, 4]中的方案的模幂运算为M₂；新方案和文献[2]方案中的n值为N₁，文献[4]方案中n值为N₂.不同协议的开销分析见表 1.

4) 计算开销.新方案的模加运算开销较文献[2, 4]的方案稍高；模乘运算开销高于文献[2]的方案，但是低于文献[4]的方案开销；模幂运算方面，新方案在加密阶段的计算开销比文献[2, 4]中方案的模幂计算次数小，同态阶段的模幂运算次数比文献[2]的方案稍高.虽然新方案总的计算开销高于文献[2]而低于文献[4].但是云外包服务安全多方计算的就是利用云服务器完成合作计算，从而减少用户的计算开销.而与文献[2, 4]相比，新方案中用户的计算开销较小，因此更能够体现云服务的价值.

5) 通信开销.文献[2]和文献[4]中的在用户加密阶段Bob需要向Alice传递用于去掉随机数的盲化向量，所以用户Alice和Bob在执行协议的过程中有1次交互.而新方案中2个参与者均不需要提前传递任何过程参数给对方，因此用户之间的通信开销为0次.

3.4 试验分析

为了进一步证实3.3节的理论分析结果，通过实验对本文协议以及文献[2, 4]协议的计算开销所需要的耗时进行对比.实验平台：win10 64位操作系统，Intel Core Ⅳ CPU 3.2 G，python 3.6编译环境.假设3个协议中双方集合势均为d=100，实验中Boneh和Paillier同态算法中的大素数p和q的位数相同, 分别取p和q为128、256、512、1 024 bit，在这4组p和q下，分别计算模幂运算M₁, M₂的耗时见表 2.

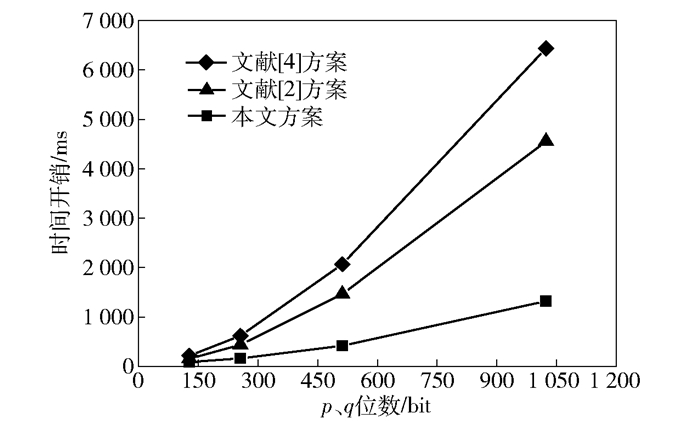
根据表 2得到的模幂运算耗时, 再由表 1可计算出3个协议在不同p和q取值时所需要的模幂运算总耗时(见图 2).其中横轴为不同的模数, 纵轴是不同模数下协议所需要的总时间.

可以看出，与文献[2, 4]的方案相比，本文方案总的计算耗时较优.

4 结束语

提出一种允许客户端外包其私有数据集并将PSI计算委托给服务器的协议.协议的关键是一个以点值形式的多项式作为集合对应多项式的表示形式.该协议允许客户端独立地完成私有数据集的转化和外包，同时也允许客户端多次在云端进行交集计算而不需要透露任何关于结果或集合的信息，也不需要重新准备集合.笔者对协议的正确性、安全性以及计算成本进行分析，结果表明协议的计算开销较优.未来将会在恶意模型下研究云外包安全两方集合计算协议.