2. 铀矿冶放射性控制技术湖南省工程研究中心, 湖南 衡阳 421001;
3. 湖南省铀尾矿库退役治理工程技术研究中心, 湖南 衡阳 421001
针对接收信号强度指示(RSSI)测距定位精度和鲁棒性差的问题,提出了一种基于秩滤波和裴波那契树的信号强度定位(RF-RSSI-FTO)算法.采用秩滤波方法对RSSI值进行去干扰滤波处理,可提高测距精度及鲁棒性;引入裴波那契树优化算法对定位坐标进行全局和局部搜索寻优处理,可减小定位误差.仿真结果表明,RF-RSSI-FTO算法能有效改善测距精度和鲁棒性,增强全局和局部搜索能力,提高定位精度.
2. Hunan Province Engineering Technology Research Center of Uranium Tailings Treatment, Hunan Hengyang 421001, China;
3. Hunan Province Engineering Research Center of Radioactive Control Technology in Uranium Mining and Metallurgy, Hunan Hengyang 421001, China
In order to solve the problem of poor ranging accuracy and robustness of received signal strength indication (RSSI), a signal strength localization algorithm based on rank filter and Fibonacci tree optimization (RF-RSSI-FTO) was proposed. First, the rank filtering method was used to remove the interference of the RSSI value to improve the accuracy and robustness of the ranging. Then, the Fibonacci tree optimization algorithm was introduced to optimize the global and local search of the positioning coordinates to reduce the positioning error. Simulation results show that the RF-RSSI-FTO algorithm can effectively improve ranging accuracy and robustness, enhance the global and local search ability, and improve positioning accuracy.
定位问题是无线传感器网络(WSN,wireless sensor network)[1-2]研究的基础和热点.目前定位算法的研究热门有基于测距和距离无关2种,基于接收信号强度指示(RSSI,received signal strength indication)的定位属于测距定位算法,通过RSSI值、理论和经验模型反映节点间距离[3-4],算法计算简单,但在实际应用中易受温度、障碍物、传播介质等环境条件干扰,造成RSSI值的偏差[5]和定位误差大.对于RSSI值干扰问题有一些较热门的解决方法,如Tseng、Zou、Svecko等[6-8]分别利用高斯滤波(GF,Gaussian filter)、无迹卡尔曼滤波(UKF,unscented Kalman filter)、粒子滤波(PF,particle filter)进行处理:采用高斯函数输出高概率区域的RSSI值,在实际测试中,多数RSSI值不符合正态分布,使得GF抗干扰能力弱;UKF虽能估计动态系统的状态与增强鲁棒性,但只能处理高斯噪声情况;PF解决了GF出现的问题,但当粒子退化或重采样引起粒子贫化时,其抗干扰能力下降.对于RSSI定位误差问题较热门的解决方法包括:冯秀芳等[9]利用粒子群优化(PSO,particle swarm optimization)算法对最小二乘法估算的未知节点坐标优化(IRSSI),局部搜索能力弱;Wu等[10]利用改进粒子滤波优化算法(PF-RSSI),以随机样本一致性缩短收敛时间,未能定位结果优化;张松海等[11]用裴波那契树优化(FTO,Fibonacci tree optimization)算法对全局最优化问题求解,相比优于PSO算法,且收敛性强,不会陷入局部最优.
综上,笔者提出基于秩滤波(RF,rank filter)和裴波那契树的信号强度定位(RF-RSSI-FTO)算法.先利用RF滤波处理RSSI值来优化测距,再采用FTO算法对未知节点估计坐标进行寻优,提高定位精度.
1 RSSI测距理论通过收发节点信号强度计算传输损耗,从而反映节点距离,利用对数-常态分布模型进行计算,如
| $ {R_s}\left( d \right) = {R_s}\left( {{d_0}} \right) - 10\beta \lg \left( {\frac{d}{{{d_0}}}} \right) $ | (1) |
其中:d为收发两端距离,单位为m;d0为参考距离,通常取1 m;Rs(d)为距离发射端dm处的信号强度,单位为dBm;Rs(d0)为d0处待定节点的信号强度,单位为dBm;β为路径长度与路径损耗比例因子.
2 定位算法改进理论RF-RSSI-FTO算法定位的整体基本思路是:先采用RF方法对RSSI值滤波进行去干扰处理,以提高RSSI测距的精度,再通过FTO算法对未知节点坐标定位进行寻优计算,减少定位误差.
2.1 秩滤波RSSI测距优化RF是基于秩统计量原理提出的,适用于高斯分布非线性的数据滤波处理,且多数RSSI值属于非高斯加性噪声.工程环境中,设RSSI为非线性离散系统,其一般方程如
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{X}}_k} = f\left( {{\mathit{\boldsymbol{X}}_{k - 1}}} \right) + {\mathit{\boldsymbol{W}}_{k - 1}}}\\ {{\mathit{\boldsymbol{Z}}_{k - 1}} = h\left( {{\mathit{\boldsymbol{X}}_k}} \right) + {\mathit{\boldsymbol{V}}_k}} \end{array} $ | (2) |
其中:Xk和Zk分别为k时刻状态向量和测量向量,f(·)和h(·)为非线性向量函数,Wk和Vk分别为k时刻系统噪声向量和测量噪声向量,其方差矩阵分别为Qk和Rk,且满足:
| $ \left. {\begin{array}{*{20}{l}} {\text{Cov}\left[ {{\mathit{\boldsymbol{W}}_k},{\mathit{\boldsymbol{W}}_l}} \right] = {\mathit{\boldsymbol{Q}}_k}{\delta _{kl}}}\\ {\text{Cov}\left[ {{\mathit{\boldsymbol{V}}_k},{\mathit{\boldsymbol{V}}_l}} \right] = {\mathit{\boldsymbol{R}}_k}{\delta _{kl}}}\\ {\text{Cov}\left[ {{\mathit{\boldsymbol{W}}_k},{\mathit{\boldsymbol{W}}_l}} \right] = 0} \end{array}} \right\} $ | (3) |
其中:Cov[·]表示协方差,δkl表示δ函数,k、l表示时刻,且满足:
| $ \left. {\begin{array}{*{20}{l}} {{\delta _{kl}} = 1,}&{k = l}\\ {{\delta _{kl}} = 0,}&{k \ne l} \end{array}} \right\} $ | (4) |
根据RF理论[12]得出加性噪声的非高斯分布秩样本集合{Xk-1, v},如
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{X}}_{k - 1,v}} = }\\ {\left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\hat X}}}_{k - 1}} + {r_j}{u_{{p_j}}}{{(\sqrt {{\mathit{\boldsymbol{P}}_{k - 1}}} )}_v},}&{v = 1, \cdots ,n}\\ {{{\mathit{\boldsymbol{\hat X}}}_{k - 1}} - {r_j}{u_{{p_j}}}{{(\sqrt {{\mathit{\boldsymbol{P}}_{k - 1}}} )}_{v - n}},}&{v = n + 1, \cdots ,2n}\\ {{{\mathit{\boldsymbol{\hat X}}}_{k - 1}} + {r_j}{u_{{p_j}}}{{(\sqrt {{\mathit{\boldsymbol{P}}_{k - 1}}} )}_{v - 2n}},}&{v = 2n + 1, \cdots ,3n}\\ {{{\mathit{\boldsymbol{\hat X}}}_{k - 1}} - {r_j}{u_{{p_j}}}{{(\sqrt {{\mathit{\boldsymbol{P}}_{k - 1}}} )}_{v - 3n}},}&{v = 3n + 1, \cdots ,4n} \end{array}} \right.} \end{array} $ | (5) |
其中:Xk-1, v为多维向量Xk-1的第v个样本点,共4n个样本点;
由k-1时刻
1) 时间更新.状态一步预测,如式(6)~(9)所示.
| $ {{\mathit{\boldsymbol{\hat X}}}_{k/k - 1}} = \frac{1}{{4n}}\sum\limits_{v = 1}^{4n} {{\mathit{\boldsymbol{X}}_{k/k - 1,v}}} $ | (6) |
| $ {\mathit{\boldsymbol{X}}_{k/k - 1,v}} = f\left( {{\mathit{\boldsymbol{X}}_{k - 1,v}}} \right) + \mathit{\boldsymbol{E}}\left[ {{\mathit{\boldsymbol{W}}_{k - 1}}} \right] $ | (7) |
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}_{k/k - 1}} = \frac{{{r^*}}}{\omega }\sum\limits_{v = 1}^{4n} {\left\{ {\left( {{\mathit{\boldsymbol{X}}_{k/k - 1,v}} - {{\mathit{\boldsymbol{\hat X}}}_{k/k - 1}}} \right) \times } \right.} }\\ {\left. {{{\left( {{\mathit{\boldsymbol{X}}_{k/k - 1,v}} - {{\mathit{\boldsymbol{\hat X}}}_{k/k - 1}}} \right)}^{\rm{T}}}} \right\} + {\mathit{\boldsymbol{Q}}_{k - 1}}} \end{array} $ | (8) |
| $ \omega = \sum\limits_{j = 1,j \ne m + 1}^{2m + 1} {r_j^2} u_{{p_j}}^2 $ | (9) |
其中:E[·]表示数学期望,r*为协方差修正系数,ω为协方差权重系数,Pk/k-1为误差的方差矩阵.
2) 测量更新.重新秩采样,如
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{X}}_{k/k - 1,v}} = }\\ {\left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\hat X}}}_{k/k - 1}} + {r_j}{u_{{p_j}}}{{(\sqrt {{\mathit{\boldsymbol{P}}_{k/k - 1}}} )}_v},}&{v = 1, \cdots ,n}\\ {{{\mathit{\boldsymbol{\hat X}}}_{k/k - 1}} - {r_j}{u_{{p_j}}}{{(\sqrt {{\mathit{\boldsymbol{P}}_{k/k - 1}}} )}_{v - n}},}&{v = n + 1, \cdots ,2n}\\ {{{\mathit{\boldsymbol{\hat X}}}_{k/k - 1}} + {r_j}{u_{{p_j}}}{{(\sqrt {{\mathit{\boldsymbol{P}}_{k/k - 1}}} )}_{v - 2n}},}&{v = 2n + 1, \cdots ,3n}\\ {{{\mathit{\boldsymbol{\hat X}}}_{k/k - 1}} - {r_j}{u_{{p_j}}}{{(\sqrt {{\mathit{\boldsymbol{P}}_{k/k - 1}}} )}_{v - 3n}},}&{v = 3n + 1, \cdots ,4n} \end{array}} \right.} \end{array} $ | (10) |
k时刻的状态估计
| $ \left. {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\hat X}}}_k} = {{\mathit{\boldsymbol{\hat X}}}_{k/k - 1}} + {\mathit{\boldsymbol{K}}_k}\left( {{\mathit{\boldsymbol{Z}}_k} - {{\mathit{\boldsymbol{\hat Z}}}_{k/k - 1}}} \right)}\\ {{\mathit{\boldsymbol{P}}_k} = {\mathit{\boldsymbol{P}}_{k/k - 1}} - {\mathit{\boldsymbol{K}}_k}{\mathit{\boldsymbol{P}}_{ZZ}}\mathit{\boldsymbol{K}}_k^{\rm{T}}}\\ {{\mathit{\boldsymbol{K}}_k} = {\mathit{\boldsymbol{P}}_{XZ}}\mathit{\boldsymbol{P}}_{ZZ}^{ - 1}} \end{array}} \right\} $ | (11) |
优化求解,如式(12)~(15)所示.
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Z}}_{k/k - 1,v}} = h\left( {{\mathit{\boldsymbol{X}}_{k/k - 1,v}}} \right) + \mathit{\boldsymbol{E}}\left[ {{\mathit{\boldsymbol{V}}_k}} \right],}\\ {v = 1,2, \cdots ,4n} \end{array} $ | (12) |
| $ {{\mathit{\boldsymbol{\hat Z}}}_{k/k - 1}} = \frac{1}{{4n}}\sum\limits_{v = 1}^{4n} {{\mathit{\boldsymbol{Z}}_{k/k - 1,v}}} $ | (13) |
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}_{ZZ}} = \frac{{{r^*}}}{\omega }\sum\limits_{v = 1}^{4n} {\left\{ {\left( {{\mathit{\boldsymbol{Z}}_{k/k - 1,v}} - {{\mathit{\boldsymbol{\hat Z}}}_{k/k - 1}}} \right)\left( {{\mathit{\boldsymbol{Z}}_{k/k - 1,v}} - } \right.} \right.} }\\ {\left. {{{\left. {{{\mathit{\boldsymbol{\hat Z}}}_{k/k - 1}}} \right)}^{\rm{T}}}} \right\} + {\mathit{\boldsymbol{R}}_k}} \end{array} $ | (14) |
| $ {\mathit{\boldsymbol{P}}_{XZ}} = \frac{{{r^*}}}{\omega }\sum\limits_{v = 1}^{4n} {\left\{ {\left( {{\mathit{\boldsymbol{X}}_{k/k - 1,v}} - {{\mathit{\boldsymbol{\hat X}}}_{k/k - 1}}} \right){{\left( {{\mathit{\boldsymbol{Z}}_{k/k - 1,v}} - {{\mathit{\boldsymbol{\hat Z}}}_{k/k - 1}}} \right)}^{\rm{T}}}} \right\}} $ | (15) |
k时刻输出的状态估计量
上述测距优化理论就是以提出的RF方法对RSSI测距干扰进行滤波处理,可大大减少RSSI值受环境中的各种扰动影响,提高了测距的稳定性、鲁棒性和精度.
2.2 裴波那契树RSSI定位方法采用FTO算法来优化节点定位,通过全局搜索和局部寻优交替迭代来寻找最优解,具有优化效果好、收敛速度快、定位精度高等优点.
2.2.1 FTO算法寻优基本思想FTO结构模型(全局模型)结合2个迭代规则来构建多维裴波那契树,规则1和规则2的主要功能分别为全局搜索和局部搜索.设FTO算法中处理点集为S,集合大小满足裴波那契数列,即|S|=Fi.
1) 规则1.令结构模型端点{La}=S,
2) 规则2.结构模型的端点La=Lbest∈S,且为S中当前最优解,{Lb}={L∈S∧L≠La},求出分割点集合{Lpa2}.
2个规则迭代完成后,合并S、新的端点和分割点,保留前Fi+1个较优点,丢弃其余点,更新点集S,同时集合大小更新为|S|=Fi+1.
提出的FTO算法思想是通过裴波那契数列近似黄金分割法,对多维欧氏空间估计待定位的处理点进行全局及局部搜索迭代寻优,即生成多维裴波那契树,最终收敛点作为处理点的位置坐标,以减少节点定位误差.
2.2.2 FTO定位搜索模型FTO算法中规则1进行全局搜索、规则2进行局部搜索,分别产生不同的分割点集,结合目标区域随机布置的节点,建立全局和局部定位搜索模型,分别如图 1、图 2所示.
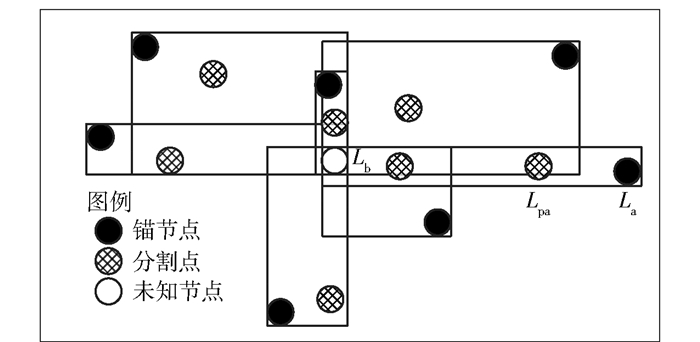
|
图 1 全局定位搜索模型 |
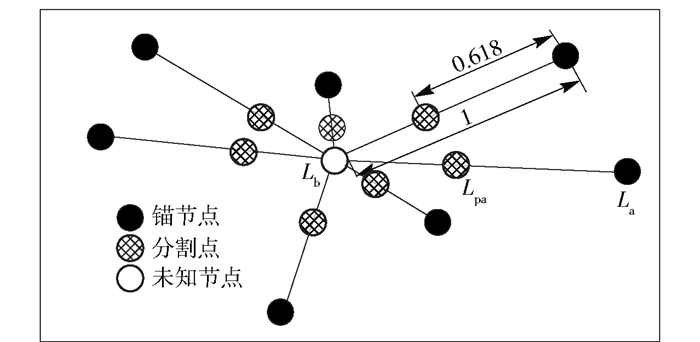
|
图 2 局部定位搜索模型 |
FTO算法通过寻优生成多维裴波那契树来接近待定位点的真实坐标,其寻优过程的各个未知节点坐标定位方法相同,在此介绍一个未知节点坐标定位,步骤如下.
步骤1 通过极大似然估计法获得未知节点估计坐标为(x′, y′), 锚节点坐标为(xλ, yλ),λ=1, 2, …, ζ,锚节点与未知节点距离为d1, d2, …, dζ,建立方程组:
| $ \left. {\begin{array}{*{20}{c}} {{{\left( {{x^\prime } - {x_1}} \right)}^2} + {{\left( {{y^\prime } - {y_1}} \right)}^2} = d_1^2}\\ {{{\left( {{x^\prime } - {x_2}} \right)}^2} + {{\left( {{y^\prime } - {y_2}} \right)}^2} = d_2^2}\\ \vdots \\ {{{\left( {{x^\prime } - {x_\zeta }} \right)}^2} + {{\left( {{y^\prime } - {y_\zeta }} \right)}^2} = d_\zeta ^2} \end{array}} \right\} $ | (16) |
令fλ=(x′-xλ)2+(y′-yλ)2,则适应度函数如:
| $ {H_{\rm{ \mathsf{ λ} }}} = \frac{1}{\zeta }\sum\limits_{\lambda = 1}^\zeta {\left| {{f_\lambda } - {d_{\rm{b}}}} \right|} $ | (17) |
其中:db为测量所得的锚节点与未知节点的距离,Hλ的极小值点坐标作为定位坐标.
步骤2 初始化各参数.设定裴波那契数列大小为Fπ.设锚节点坐标与未知节点估计坐标集合为S,集合大小为|S|=Fi.分割点坐标为(xpa,ypa),则二维欧氏空间黄金分割表达式为
| $ \begin{array}{*{20}{c}} {\left| {\sqrt {\frac{{{{\left( {{x_{{\rm{pa}}}} - {x_\lambda }} \right)}^2} + {{\left( {{y_{{\rm{pa}}}} - {y_\lambda }} \right)}^2}}}{{{{\left( {{x_\lambda } - {x^\prime }} \right)}^2} + {{\left( {{y_\lambda } - {y^\prime }} \right)}^2}}}} } \right| = }\\ {\left| {\sqrt {\frac{{{{\left( {{x_{{\rm{pa}}}} - {x^\prime }} \right)}^2} + {{\left( {{y_{{\rm{pa}}}} - {y^\prime }} \right)}^2}}}{{{{\left( {{x_\lambda } - {x_{{\rm{pa}}}}} \right)}^2} + {{\left( {{y_\lambda } - {y_{{\rm{pa}}}}} \right)}^2}}}} } \right| = \frac{{{F_i}}}{{{F_{i + 1}}}} = \alpha } \end{array} $ | (18) |
步骤3 按规则1,确定随机生成的未知节点估计坐标集为{Lb}和分割点坐标集为{Lpa1}.
步骤4 按规则2,生成新的分割点坐标集为{Lpa2}.
步骤5 合并S、{Lb}、{Lpa1}、{Lpa2},将合并后的所有点坐标值代入适应度函数式(17),进行误差比较,保留前Fi+1个误差小的点坐标作为更新点集S,大小变成|S|=Fi+1.
步骤6 比较点集|S|与设定的Fπ大小,若等于Fπ,继续进行步骤7;反之回到步骤3.
步骤7 判断迭代次数是否达到最大迭代次数,若未达到,回到步骤3;否则结束循环.此时收敛的Hλ极小值点坐标(最优)作为待定位点坐标.
3 仿真分析仿真分两部分:基于RF的测距精度与同类算法对比;RF-RSSI-FTO算法与同类算法对比.仿真软件均采用Matlab2017.
3.1 测距优化仿真通过仿真对比GF、UKF、PF与RF在非高斯加性噪声情况下的测距优化性能.选取TICC2530无线传感节点模块发送、接收RSSI信号,实验环境选取湖南省某矿山,测量距离30 m,间隔0.5 m测一组,每组数据测50次求平均值. 图 3所示为仿真测距误差对比.
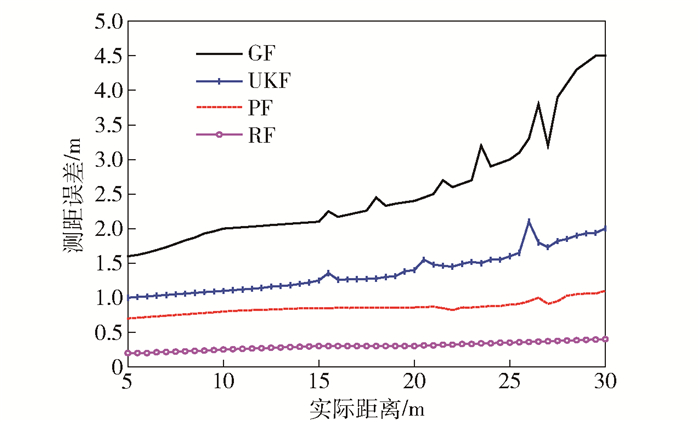
|
图 3 测距误差对比 |
从图 3中可看出,相比PF、UKF、GF的RSSI测距,RF的整体测距误差值最小,且明显. RF平均测距误差为0.35 m, 分别是PF、UKF和GF平均测距误差的37.8%、20.9%、10.7%,且RF的误差波动较小,表明了RF对RSSI值滤波处理后的测距值误差小,鲁棒性强.
3.2 定位误差仿真选取归一化的平均定位误差eη作为评价指标,有
| $ {e_\eta } = \frac{{\sum\limits_{\eta = 1}^N {\sqrt {{{\left( {x_\eta ^\prime - {x_\eta }} \right)}^2} + {{\left( {y_\eta ^\prime - {y_\eta }} \right)}^2}} } }}{N} \times 100\% $ | (19) |
其中:N为节点总数,(xη, yη)为η节点的真实坐标,(x′η, y′η)为η节点的估计坐标.
1) 仿真网络拓扑结构为区域节点随机生成,通信半径用R表示,设区域面积为200 m×200 m,最大通信半径为50 m,未知节点数100个,锚节点数20个.将RF-RSSI-FTO算法与IRSSI、PF-RSSI算法的定位误差进行比较,仿真实验重复50次,图 4为仿真定位误差对比. RF-RSSI-FTO算法的定位误差基本位于0.5~0.8 m,IRSSI定位误差位于0.9~1.2 m,PF-RSSI定位误差位于1.2~1.4 m,RF-RSSI-FTO算法定位误差比另外2种算法分别下降了38.1%、50.0%.
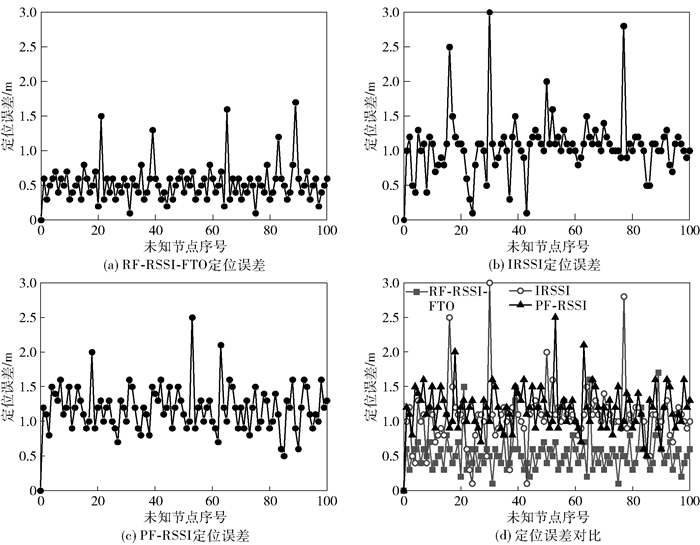
|
图 4 3种算法下的定位误差 |
2) 锚节点密度、通信半径、节点总数3个因素对无线传感器网络定位有较大影响,下面从这3个方面分析RF-RSSI-FTO算法的定位性能.
在仿真区域随机布置200个节点(含锚节点),通信半径设为50 m,锚节点密度改变时,3种算法的定位误差对比如图 5所示. 3种算法定位误差均随锚节点个数增加而减小,RF-RSSI-FTO算法定位误差最小,且定位误差整体明显小于其他2种算法,其平均定位误差为0.31 m,分别是IRSSI和PF-RSSI的41.3%、34.9%,且当锚节点个数大于20时,RF-RSSI-FTO定位误差最先趋于稳定.
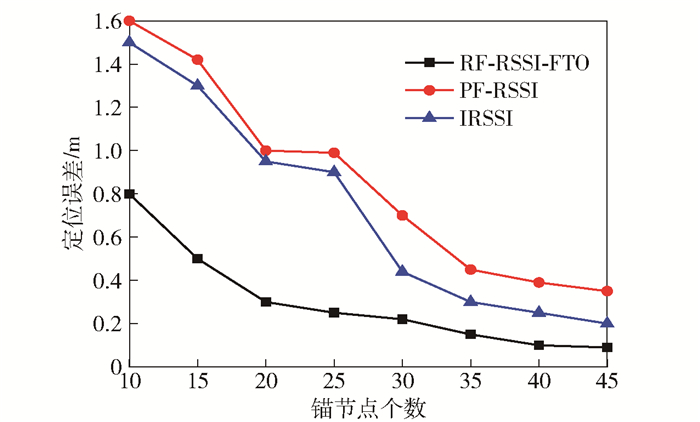
|
图 5 不同锚节点密度下定位误差对比 |
在仿真区域布设200个节点,其中锚节点个数为30,通信半径改变时,3种算法的定位误差对比如图 6所示.图中显示出各算法定位误差随通信半径增加而减小,这是因为通信半径增大,无线传感器网络的连通度也增大. RF-RSSI-FTO算法的整体定位误差最小,其平均定位误差为0.51 m,分别是IRSSI和PF-RSSI的47.3%、34.7%,明显优于其他2种算法.
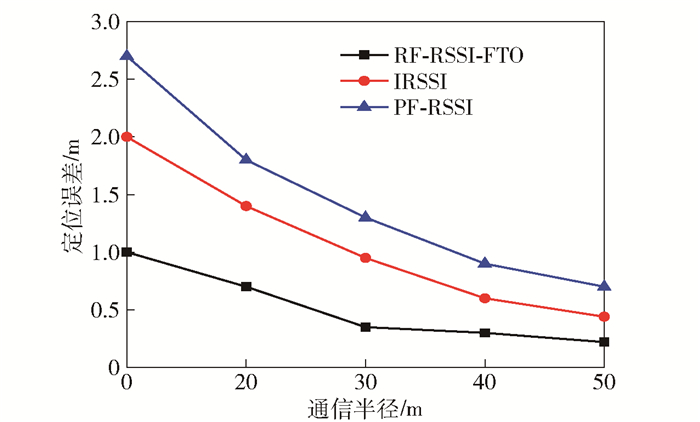
|
图 6 不同通信半径下的定位误差对比 |
在仿真区域布设20个锚节点(包含于节点总数中),通信半径为50 m,节点总数改变时,3种算法的定位误差对比如图 7所示. RF-RSSI-FTO算法明显优于其他2种算法,且定位误差最小,平均定位误差为0.22 m,分别是IRSSI和PF-RSSI的32.5%、25%. 3种算法的定位误差均随节点总数增加而减小,这是因为增加了单位通信范围内的节点数量,有利于全局搜索优化,但定位误差曲线变化平缓,表明节点总数对定位误差的影响因子较低.

|
图 7 不同节点总数下的定位误差对比 |
针对RSSI测距容易受环境因素干扰、鲁棒性差及定位精度不高的特点,提出了一种基于秩滤波和裴波那契树的RSSI定位(RF-RSSI-FTO)算法.利用RF对RSSI值进行去干扰滤波处理,较大地提高了测距精度及鲁棒性,再通过FTO算法对定位坐标进行全局和局部搜索寻优处理,进一步降低了定位误差.通过仿真对比RF、UKF、PF、GF 4种滤波处理RSSI测距误差及稳定性,结果表明,RF的测距精度及鲁棒性明显优于其他3种;从锚节点密度、通信半径、节点总数3个方面,仿真对比RF-RSSI-FTO、IRSSI、PF-RSSI 3种算法的定位误差,结果表明,RF-RSSI-FTO算法有较好的定位精度.
| [1] |
常小凯, 朱婉婕, 李德奎. 三维无线传感器网络定位的可行方向算法[J]. 北京邮电大学学报, 2016, 39(2): 98-102. Chang Xiaokai, Zhu Wanjie, Li Dekui. A feasible direction algorithm for solving 3D sensor network localization[J]. Journal of Beijing University of Posts and Telecommunications, 2016, 39(2): 98-102. |
| [2] |
何杰, 吴得泱, 李希飞, 等. 利用测距值优化的室内三维定位算法[J]. 北京邮电大学学报, 2017, 40(3): 37-42. He Jie, Wu Deiyang, Li Xifei, et al. A 3-D indoor localization algorithm using distance optimization[J]. Journal of Beijing University of Posts and Telecommunications, 2017, 40(3): 37-42. |
| [3] |
Mardini W, Khamayseh Y, Almodawar A A, et al. Adaptive RSSI-based localization scheme for wireless sensor networks[J]. Peer-to-Peer Networking and Applications, 2016, 9(6): 991-1004. DOI:10.1007/s12083-015-0370-y |
| [4] |
Zhou Cheng, Yuan Jiazheng, Liu Hongzhe, et al. Bluetooth indoor positioning based on RSSI and Kalman filter[J]. Wireless Personal Communications, 2017, 96(3): 4115-4130. DOI:10.1007/s11277-017-4371-4 |
| [5] |
Guan Bo, Li Xin. An RSSI-based wireless sensor network localization algorithm with error checking and correction[J]. International Journal of Online and Biomedical Engineering, 2017, 13(12): 52-66. DOI:10.3991/ijoe.v13i12.7892 |
| [6] |
Tseng C H, Yen J S. Enhanced Gaussian mixture model of RSSI purification for indoor positioning[J]. Journal of Systems Architecture, 2017, 81(11): 1-6. |
| [7] |
Zou Tengyue, Lin Shouying, Li Shuyuan. Blind RSSD-based indoor localization with confidence calibration and energy control[J]. Sensors, 2016, 16(6): 788-811. DOI:10.3390/s16060788 |
| [8] |
Svecko J, Malajner M, Gleich D. Distance estimation using RSSI and particle filter[J]. ISA Transactions, 2015, 55(16): 275-285. |
| [9] |
冯秀芳, 吕淑芳. 基于RSSI和分步粒子群算法的无线传感器网络定位算法[J]. 控制与决策, 2014, 29(11): 1966-1972. Feng Xiufang, Lü Shufang. Wireless sensor networks locating algorithm based on RSSI and split-step particle swarm optimization algorithm[J]. Control and Decision, 2014, 29(11): 1966-1972. |
| [10] |
Wu Zheng, Jedari E, Muscedere R, et al. Improved particle filter based on WLAN RSSI fingerprinting and smart sensors for indoor localization[J]. Computer Communications, 2016, 83(3): 64-71. |
| [11] |
张松海, 施心陵, 李鹏, 等. 多峰函数优化的黄金分割斐波那契树优化算法[J]. 电子学报, 2017, 45(4): 791-798. Zhang Songhai, Shi Xinling, Li Peng, et al. Golden section Fibonacci tree optimization algorithm for multimodal function optimization[J]. Acta Electronic Sinica, 2017, 45(4): 791-798. |
| [12] |
傅惠民, 肖强, 娄泰山, 等. 非线性非高斯秩滤波方法[J]. 航空动力学报, 2015, 30(10): 2318-2322. Fu Huimin, Xiao Qiang, Lou Taishan, et al. Nonlinear and non-Guassian rank filter method[J]. Journal of Aerospace Power, 2015, 30(10): 2318-2322. |
| [13] |
董易, 吕丹桔, 王霞, 等. 斐波那契树优化算法全局随机性概率收敛分析[J]. 控制与决策, 2018, 33(3): 439-446. Dong Yi, Lü Danjv, Wang Xia, et al. A global randomness-based probability convergence analysis of Fibonacci tree optimization algorithm[J]. Control and Decision, 2018, 33(3): 439-446. |


