2. 北京邮电大学 可信分布式计算与服务教育部重点实验室, 北京 100876;
3. 北京邮电大学 移动互联网安全技术国家工程实验室, 北京 100876
针对通信资源调度场景下的多智能体强化学习(MARL)问题,提出了对称MARL问题以及三类对称性的定义和条件,并定义了策略融合和策略误差;针对强对称MARL问题,定义了三类评价指标,并对策略估计误差进行分析,提出了强对称MARL问题的策略误差定理及推论.针对无线通信的接入控制问题建立了MARL问题,仿真结果验证了强对称MARL问题策略估计误差的特性.结果表明,可以使用低复杂度的MARL子问题对高复杂度的强对称MARL问题进行策略估计,且策略估计误差和对网络性能的影响均较小.
2. Key Laboratory of Trustworthy Distributed Computing and Service(Ministry of Education), Beijing University of Posts and Telecommunications, Beijing 100876, China;
3. National Engineering Laboratory for Mobile Network Security, Beijing University of Posts and Telecommunications, Beijing 100876, China
Considering multi-agent reinforcement learning (MARL) theory in communication resource scheduling scenario, the symmetrical MARL problem was proposed with definitions for three types of symmetry properties and analysis of policy estimation error. The policy estimation error theorem for strong symmetrical MARL was presented. Simulation results based on the admission control problem in wireless system were modeled by MARL, which testify the characteristics of policy estimation error for strong symmetrical MARL problems. It shows that using the MARL sub-problems with low computational complexity to estimate the original MARL problem with high computational complexity only brings small policy estimation error and deterioration of system performance.
近年来,机器学习技术已成为全球热点.作为机器学习技术的重要分支,强化学习(RL, reinforcement learning)技术与马尔可夫决策过程(MDP, Markov decision process)模型因其无需海量训练数据标注、可与控制理论相结合等优点而成为研究热点[1-4],并广泛应用于跨学科领域的理论研究.例如,在移动通信系统的资源调度技术领域内,使用RL与MDP理论解决接入控制[5]、数据包调度[6]等技术问题是较为常见的技术路线.由于RL与MDP理论存在着模型不可知、维数复杂度灾难、难以复现等问题,目前RL与MDP的研究主要集中在大规模RL、状态-行动空间泛化、策略估计与误差分析等理论方面[1].
多智能体强化学习(MARL, multi-agent RL)是RL理论的重要分支,通常建模为处于同一观测环境的多个智能体进行协同策略优化的RL问题,属于大规模RL问题的一种特殊场景[2-4]. MARL理论的发展较为缓慢,大量结论主要依赖于基于博弈论的理论分析[4],且尚未与RL领域前沿理论,如深度Q网络(DQN, deep Q network)等充分结合[3].由于MARL可以等同于状态行动空间较大的RL问题,故使用大规模RL理论可以解决MARL问题,因而尚未受到广泛关注.此外,MARL问题所具有的环境对称性等特性仅在某些特殊场景中存在,对该类对称特性的研究尚未明确,因而限制了MARL理论的发展.
考虑一种常见于通信系统资源调度模型中的大规模RL问题,例如,接入控制问题[7],可以建模为MARL问题.当MARL的状态、行动均为高维向量时,由于状态-行动空间尺寸过大,传统的基于模型的RL求解算法无法遍历空间内的状态-行动空间对,可采用状态-行动空间泛化并借助非线性逼近器来求解最优策略,例如策略梯度法、DQN法等.但这些问题并没有考虑并利用实际问题场景中存在的对称性.例如,多小区用户接入控制问题[5, 7]中,本小区的新用户到达速率与其相邻小区用户数量有关,在只考虑本小区用户的情况下,其他小区的用户数可看作决定移动性的参数,不影响本小区的目标函数.基于此思路,提出一种对称MARL理论,并提出了策略估计方法,从理论上分析了估计误差的收敛性.利用无线通信系统的接入控制问题对该理论进行了仿真验证.
1 对称MARL问题及其定义考虑一类高维MARL问题,其状态定义为
| $ \mathit{\boldsymbol{s}} = \left( {{s_1},{s_2}, \cdots ,{s_K}} \right) $ | (1) |
其中:sk∈Sk, Sk={1, …,Nk}, s∈S,
| $ \mathit{\boldsymbol{a}} = \left( {{\mathit{\boldsymbol{a}}_1},{\mathit{\boldsymbol{a}}_2}, \cdots ,{\mathit{\boldsymbol{a}}_K}} \right) $ | (2) |
其中:可行状态ak∈Ak, a∈A,
| $ \mathop {\min }\limits_\pi {J_\pi }\left( {{\mathit{\boldsymbol{s}}_0}} \right) = \mathop {\min }\limits_\pi \mathop {\lim \sup }\limits_{T \to \infty } \frac{1}{T}E\left\{ {\sum\limits_{t = 0}^{T - 1} G \left( {{\mathit{\boldsymbol{s}}_t},{\mathit{\boldsymbol{a}}_t}} \right)} \right\} $ | (3) |
为方便理论分析,采用基于模型的方法进行推导.定义概率测度p:SSA→[0, 1],令p(st, st+1, at)表示t时刻在状态st选取行动at后,下一时刻转移到状态st+1的概率.在该概率测度完全可知的情况下,该问题可以转化为动态规划问题,并采用标准算法求解.
考虑该模型在实际环境时,尤其是在通信网络的调度场景时,依据排队论对该概率进行建模时,其表达式常具有对称性,并可利用该对称性将一个高维的MARL问题近似分解为低维RL问题.为了刻画这种对称性,首先给出MARL子问题的定义.
定义1 MARL子问题.
对于具有形式如式(1)~式(3)的MARL问题,定义为MARL问题{s, a, G, p},其子问题k定义为{sk, ak, Gk, pk},其中,sk、ak的定义与式(1)、式(2)相同,子问题回报函数为Gk:SkAk→
| $ \mathop {\min }\limits_{{\pi _k}} {J_{{\pi _k}}}\left( {{s_{k,0}}} \right) = \mathop {\min }\limits_{{\pi _k}} \mathop {\lim \sup }\limits_{T \to \infty } \frac{1}{T}E\left\{ {\sum\limits_{t = 0}^{T - 1} {{G_k}} \left( {{s_{k,t}},{\mathit{\boldsymbol{a}}_{k,t}}} \right)} \right\} $ | (4) |
概率测度pk:SkSkAk→[0, 1],pk(sk, t, sk, t+1, ak, t)表示t时刻在状态sk, t选取行动ak, t后,下一时刻转移到状态sk, t+1的概率.
根据定义1,子问题{sk, ak, Gk, pk}相当于独立观察状态sk的变化,并做出相应决策.显然,若子问题是相互独立的,原问题将可以分解成K个子问题,其最优策略也应是各子问题最优策略的简单叠加.然而当子问题之间存在相关性,或者原问题无法直接分解为具有定义1形式的子问题,那么子问题策略的叠加将会与原问题的策略存在偏差,称之为策略估计误差.为了刻画上述现象,给出以下定义及其所满足的条件.
定义2 MARL问题的独立性和对称性.
考虑MARL问题{s, a, G, p}及其子问题{sk, ak, Gk, pk},并给出下列条件.
条件1:空间对称性.
| $ S = \bigcup\limits_k {{S_k}} $ | (5) |
| $ A = \bigcup\limits_k {{A_k}} $ | (6) |
条件2:回报可加性.
| $ G\left( {{\mathit{\boldsymbol{s}}_t},{\mathit{\boldsymbol{a}}_t}} \right) = \sum {{G_k}} \left( {{s_{k,t}},{\mathit{\boldsymbol{a}}_{k,t}}} \right),\forall t $ | (7) |
条件3:状态转移独立性.
| $ p\left( {{\mathit{\boldsymbol{s}}_t},{\mathit{\boldsymbol{s}}_{t + 1}},{\mathit{\boldsymbol{a}}_t}} \right) = \prod {{p_k}} \left( {{s_{k,t}},{s_{k,t + 1}},{\mathit{\boldsymbol{a}}_{k,t}}} \right),\forall t $ | (8) |
若同时满足条件1~条件3,则各MARL子问题相互独立,称MARL问题{s, a, G, p}为对称独立RL问题;若只满足条件1和条件2,称其为强对称MARL问题;若只满足条件1,称其为弱对称MARL问题.
显然,对于对称独立MARL问题{s, a, G, p},相当于K个相互独立RL子问题{sk, ak, Gk, pk}的叠加,其最优策略也应当为各子问题最优策略的叠加.为了刻画上述现象,给出策略融合算子的定义.
定义3 策略融合算子.
考虑RL子问题{sk, ak, Gk, pk},其策略记为πk={μk, μk, …}, μk:Sk→Ak.定义策略融合算子
| $ \bar \pi \buildrel \Delta \over = \uplus \left( {{\pi _1}, \cdots ,{\pi _K}} \right) $ | (9) |
其中:新策略π={μ, μ, …}, μ:S→A为融合策略,满足
| $ \bar S = \bigcup\limits_k {{S_k}} $ | (10) |
对任意s∈S,按新策略产生的行动记为a,满足
| $ \mathit{\boldsymbol{\bar a}} = \text{vec}\left( {{\mathit{\boldsymbol{a}}_1}, \cdots ,{\mathit{\boldsymbol{a}}_k}} \right) $ | (11) |
即各子问题行动按下标顺序叠加产生新行动.
根据策略融合算子的定义,对于对称独立MARL问题{s, a, G, p},其子问题的融合策略应当与该问题的策略相同.为了度量策略的差异,定义策略误差.
定义4 策略误差.
对于定义在同一状态空间S上的策略π和π,其策略误差为
| $ \delta (\bar \pi ,\pi ) \buildrel \Delta \over = \frac{1}{{\left| S \right|}}\sum\limits_{\mathit{\boldsymbol{s}} \in S} {\left\| {\mu (\mathit{\boldsymbol{s}}) - \bar \mu (\mathit{\boldsymbol{s}})} \right\|} $ | (12) |
其中‖·‖为定义在K维行动向量空间上的距离范数.
根据定义4,考虑对称独立MARL问题,给出如下引理.
引理1 对于对称独立MARL问题{s, a, G, p}及其子问题{sk, ak, Gk, pk},满足定义3给出的策略融合操作所得到的融合策略,其与原策略的策略误差为0,即
| $ \delta (\bar \pi ,\pi ) = 0 $ | (13) |
显然,根据对称独立MARL问题的定义,各子问题相互独立;根据策略融合的定义,新策略所产生的行动是各独立子问题的简单叠加.因此,根据独立性,各子问题的最优策略的叠加应与原问题的最优策略等价.
2 强对称MARL的策略估计误差第1节中的引理1适用于一种极端情况,即MARL问题由一组相互独立的RL子问题进行叠加而形成.但是在实际情况中,高维RL问题很难同时满足条件1~条件3.
首先考虑强对称MARL问题.根据定义,强对称MARL问题依然可以看成一组RL子问题的叠加,但是RL子问题之间不独立,即某子问题的状态转移概率不仅由该子问题的状态和行动决定,同时也受其他子问题的影响.显然,这种影响越小,子问题的融合策略与原问题策略之间的误差就越小.显然,由于各子问题存在相关性,单独观测子问题将导致子问题的状态转移呈现非平稳特性,也将导致融合策略与原问题的策略呈现差异,即策略估计误差.为了刻画这种现象,定义MARL问题的转移概率对数似然比.
定义5 转移概率对数似然比.
考虑MARL问题{s, a, G, p}及其子问题{sk, ak, Gk, pk},定义转移概率对数似然比为
| $ L = \ln \frac{{\prod {{p_k}} \left( {{s_{k,t}},{s_{k,t + 1}},{\mathit{\boldsymbol{a}}_{k,t}}} \right)}}{{p\left( {{\mathit{\boldsymbol{s}}_t},{\mathit{\boldsymbol{s}}_{t + 1}},{\mathit{\boldsymbol{a}}_t}} \right)}} $ | (14) |
转移概率对数似然比表征了强对称MARL问题的相关性,即该问题不满足条件3所达到的程度.利用该定义,可以给出如下定理.
定理1 对于强对称MARL问题{s, a, G, p}及其子问题{sk, ak, Gk, pk},对于满足定义3给出的策略融合操作所得到的融合策略,其与原策略的策略误差为|L|的增函数,且
| $ \mathop {\lim }\limits_{\left| \mathscr{L} \right| \to 0} \delta (\bar \pi ,\pi )\left[ {\left| L \right|} \right] = 0 $ | (15) |
其证明由其定义可直接得到,不再赘述.
定理1给出了评价MARL可以分解为RL子问题的指标,即对于足够小的|L|,则可使用RL子问题的融合策略来逼近MARL问题的策略.但是在实际MARL问题的观测中,很难直接计算得到|L|;另一方面,对于MARL的每一个决策实体,其观测子问题的条件转移概率更为直观,且子问题转移概率的对数似然比也可以度量子问题之间的相关性.因此,定义子问题的条件转移概率.
定义6 子问题的条件转移概率和对数似然比.
考虑RL子问题{sk, ak, Gk, pk},概率测度为pk:SkSkAk→[0, 1],则给定t时刻其他子问题的观测结果Ot,其条件转移概率定义为
| $ {p_k}\left( {{s_{k,t}},{s_{k,t + 1}},{\mathit{\boldsymbol{a}}_{k,t}}|{O_t} = \left\{ {{s_{l,t}},{\mathit{\boldsymbol{a}}_{l,t}}} \right\},\forall l \ne k} \right) $ | (16) |
即在其他子问题的条件下当前子问题的转移概率,相当于将其他子问题看作环境变化.显然,该条件概率与非条件概率的差异表征了该子问题与其他子问题的相关性.定义子问题转移概率的对数似然比为
| $ {L_k}\left( {{O_t}} \right) = \ln \frac{{{p_k}\left( {{s_{k,t}},{s_{k,t + 1}},{\mathit{\boldsymbol{a}}_{k,t}}|{O_t}} \right)}}{{{p_k}\left( {{s_{k,t}},{s_{k,t + 1}},{\mathit{\boldsymbol{a}}_{k,t}}} \right)}} $ | (17) |
将MARL转移概率对数似然比代替为子问题转移概率对数似然比,结合定理1,可得如下推论.
推论1 对于强对称MARL问题{s, a, G, p}及其子问题{sk, ak, Gk, pk},对于满足定义3给出的策略融合操作所得到的融合策略,其与原策略的策略误差为max {Lk}的增函数,且
| $ \mathop {\lim }\limits_{\max \left\{ {\left| {{\mathscr{L}_k}} \right|} \right\} \to 0} \delta (\bar \pi ,\pi )\left[ {\left| L \right|} \right] = 0 $ | (18) |
为了进一步衡量状态之间的相关性,定义状态的平稳分布与边缘分布.
定义7 平稳分布、边缘分布、条件分布与分布似然比.
考虑MARL问题{s, a, G, p}及其子问题{sk, ak, Gk, pk},令π(s, a)和πk(sk, ak)分别表示MARL问题的平稳分布及其子问题的边缘分布,则可定义边缘分布为
| $ {\pi _k}\left( {{s_k},{\mathit{\boldsymbol{a}}_k}} \right) = \underbrace {\int_{{s_1}} {\int_{{\mathit{\boldsymbol{a}}_1}} { \cdots \int_{{s_K}} {\int_{{\mathit{\boldsymbol{a}}_K}} {} } } } }_{\forall \left| {{s_l},{\mathit{\boldsymbol{a}}_l}} \right|,l \ne k}\pi (\mathit{\boldsymbol{s}},\mathit{\boldsymbol{a}}) $ | (19) |
当给定t时刻其他子问题的观测结果Ot时,定义条件分布为
| $ {\pi _k}\left( {{s_{k,t}},{\mathit{\boldsymbol{a}}_{k,t}}|{O_t} = \left\{ {{s_{l,t}},{\mathit{\boldsymbol{a}}_{l,t}}} \right\},\forall l \ne k} \right) $ | (20) |
即在其他子问题的条件下当前子问题的稳态分布,则可定义状态行动联合分布似然比为
| $ {P_k}\left( {{O_t}} \right) = \log \frac{{{\pi _k}\left( {{s_{k,t}},{\mathit{\boldsymbol{a}}_{k,t}}|{O_t}} \right)}}{{{\pi _k}\left( {{s_{k,t}},{\mathit{\boldsymbol{a}}_{k,t}}} \right)}} $ | (21) |
同理,当只考虑状态时,有
| $ \pi \left( \mathit{\boldsymbol{s}} \right) = \sum\limits_\mathit{\boldsymbol{a}} {\pi (\mathit{\boldsymbol{s}},\mathit{\boldsymbol{a}})} $ | (22) |
| $ {\pi _k}\left( {{s_k}} \right) = \sum\limits_{{\mathit{\boldsymbol{a}}_k}} {{\pi _k}} \left( {{s_k},{\mathit{\boldsymbol{a}}_k}} \right) $ | (23) |
边缘分布为
| $ {\pi _k}\left( {{s_k}} \right) = \underbrace {\int_{{s_1}} { \cdots \int_{{s_K}} {} } }_{{\forall _{{s_l}}},l \ne k}\pi (\mathit{\boldsymbol{s}}) $ | (24) |
当给定Ot时,定义条件分布为
| $ {\pi _k}\left( {{s_{k,t}}|{O_t} = \left\{ {{s_{l,t}}} \right\},\forall l \ne k} \right) $ | (25) |
则可定义状态分布似然比为
| $ {{\hat P}_k}\left( {{O_t}} \right) = \ln \frac{{{\pi _k}\left( {{s_{k,t}}|{O_t}} \right)}}{{{\pi _k}\left( {{s_{k,t}}} \right)}} $ | (26) |
类似地,将子问题转移概率对数似然比代替为分布似然比,结合定理1和推论1,可得如下推论.
推论2 对于强对称MARL问题{s, a, G, p}及其子问题{sk, ak, Gk, pk},对于满足定义3给出的策略融合操作所得到的融合策略,其与原策略的策略误差为max {Pk}和
| $ \begin{array}{*{20}{c}} {\mathop {\lim }\limits_{\max \left\{ {\left| {{P_k}} \right|} \right\} \to 0} \delta (\bar \pi ,\pi )[|L|] = }\\ {\mathop {\lim }\limits_{\max \left\{ {\left| {{P_k}} \right|} \right\} \to 0} \delta (\bar \pi ,\pi )[|L|] = 0} \end{array} $ | (27) |
对比定理1及其推论可以看出,推论2的评价指标最为直观,在实际观测时根据定义7计算分布似然比,再评估策略误差,即给出强对称MARL问题策略估计误差的变化规律.
限于篇幅,针对弱对称MARL问题的理论分析以及各定理、推论的证明等不再阐述.
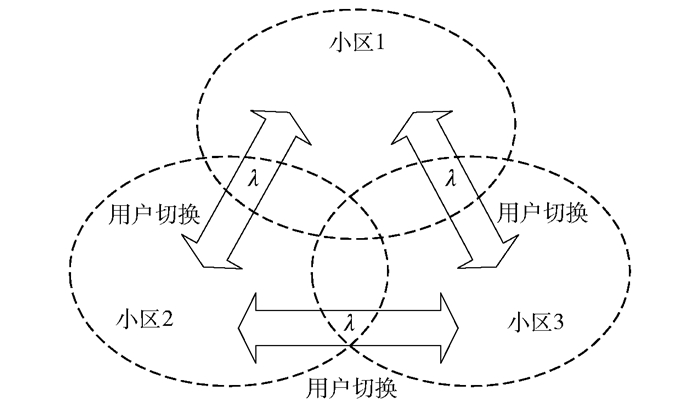
3 仿真结果为了验证策略估计误差的收敛性,考虑多小区无线通信系统中的接入控制问题,如图 1所示.由于用户的移动性,各小区内的用户将以一定的泊松事件速率向相邻小区发起切换请求.为防止网络拥塞,需执行接入控制策略[5, 7].将该问题建模为强对称MARL问题,该系统包含K个相邻小区,系统内各小区的新用户将发起业务,并产生新用户接入请求事件,邻小区用户的移动性将产生小区间切换请求事件,网络依据接入控制策略对这些请求进行决策.则系统的状态可由式(1)表示,并令Nk表示第k个小区可容纳的最大用户数,其数值可由业务的服务质量(QoS, quality of service)限制条件确定.系统的行动可由式(2)表示,其中向量ak内包含移动性决策变量,取值为0代表拒绝接入,取值为1代表允许接入;考虑小区内不同类型的用户,考察新用户和切换用户两类用户的决策行为,则ak长度为2,分别代表系统对上述两类用户的接入控制行为.系统的转移概率表达式可由移动性模型给出,其中移动性参数由各小区的用户数确定.例如,切换请求的事件速率应等于邻小区用户数量乘以单一用户发起切换请求的事件速率,即依赖于其他子问题的观测结果Ot,满足式(16)的形式.回报函数设置为与动作相关,当动作取1时意味着接受用户接入请求,给出正值常数回报;动作取0时无回报.仿真中单用户的切换事件速率设为常数λ,各事件速率单位设为呼叫每秒.模型的详细推导详见文献[7].
|
图 1 多小区用户接入控制问题 |
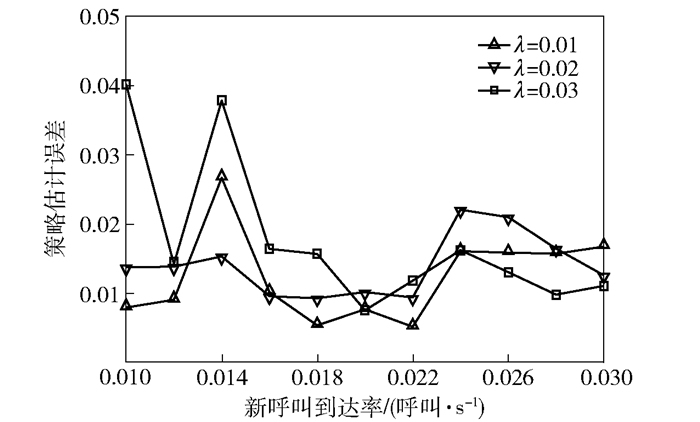
上述问题符合强对称MARL问题的定义,且具有明确的转移概率表达式和MARL子问题形式.在问题规模不大的情况下,可以使用基于模型的MDP方法求解出原问题和MARL子问题的最优策略,并通过定义3描述的策略融合方法将子问题的最优策略进行融合,得到融合策略并作为原问题的估计策略,再根据式(12)计算策略估计误差,结果如图 2所示.在不同切换事件速率λ的条件下,使用MARL策略估计方法的策略估计误差均在3%附近波动.这是由于MARL子问题之间存在相关性,单独观察MARL子问题而忽视了系统整体特性.为了进一步解释策略误差对系统性能的影响,使用原策略与估计策略进一步计算系统的性能指标.使用平均阻塞率作为评价,其计算公式如文献[7]中式(24)和式(25)所示,其物理意义为网络处于阻塞状态的概率,所得的结果如图 3所示.可以看出,由于使用了融合策略作为估计策略,网络平均阻塞率有所提升,相当于性能恶化,其原因为策略估计所带来的误差.且当切换速率λ增加时,小区之间用户移动更为频繁,导致MARL各子问题相关性增加,使得原MARL策略和融合策略之间的偏差逐渐增加.考虑到使用融合策略方法求解K个一维MARL子问题的复杂度相比原K维RL问题有显著降低,该方法相当于使用低复杂度的MARL子问题来代替高复杂度的MARL原问题.仿真结果表明,二者的偏差较小,可以在牺牲少量系统性能的情况下获得计算复杂度的大幅降低.
|
图 2 MARL策略与融合策略的估计误差 |

|
图 3 MARL策略与融合策略网络性能对比 |
针对通信资源调度场景下的MARL问题,提出了对称MARL理论,给出了3类对称性的定义.定义了策略融合和策略误差以及强对称MARL问题,结合3类评价指标对策略估计误差进行理论分析,提出了强对称MARL问题的策略误差定理.仿真结果表明,强对称MARL的融合策略与原策略的策略估计误差较小,因而可以在性能损失较小的情况下使用MARL子问题对原问题进行估计,使计算复杂度大幅度降低.下一步的研究工作包括弱对称MARL问题的理论推导以及与深度RL相结合的对称MARL理论等.
| [1] |
Sutton R S, Barto A G. Reinforcement learning:an introduction[M]. 2nd ed. Cambridge: MIT Press, 2017.
|
| [2] |
Foerster J, Nardelli N, Farquhar G, et al. Stabilizing experience replay for deep multi-agent reinforcement learning[C]//ICML 2017. Sydney: PMLR 70, 2017: 1-10.
|
| [3] |
Foerster J, Assael Y, Freitas N, et al. Learning to communicate with deep multi-agent reinforcement learning[C]//NIPS 2016. Barcelona: IEEE Press, 2016: 1-9.
|
| [4] |
Busoniu L, Babuska R, Schutter B. Multi-agent reinforcement learning: an overview[C]//Srinivasan D, Jain L C. Innovations in multi-agent systems and applications-1. Berlin: Springer, 2010: 183-221.
|
| [5] |
Yu Fei, Krishnamurthy V. Optimal joint session admission control in integrated WLAN and CDMA cellular networks with vertical handoff[J]. IEEE Transactions on Mobile Computing, 2007, 6(1): 126-139. DOI:10.1109/TMC.2007.250676 |
| [6] |
Zhou Bo, Cui Ying, Tao Meixia. Stochastic content-centric multicast scheduling for cache-enabled heterogeneous cellular networks[J]. IEEE Transacations on Wireless Communications, 2016, 15(9): 6284-6297. DOI:10.1109/TWC.2016.2582689 |
| [7] |
Zhang Xinran, Jin Hao, Ji Xiaodong, et al. A separate-SMDP approximation technique for RRM in heterogeneous wireless networks[C]//WCNC 2012. New York: IEEE Press, 2012: 2087-2091.
|



