2. 教育部宽带无线通信与传感网技术重点实验室, 南京 210003
为了有效提升轨道角动量(OAM)态的检测效率,提出一种基于快速傅里叶变换(FFT)的OAM态成分检测方法.在马赫曾德尔干涉仪2臂上加入道威棱镜,其中一个道威棱镜设置为0,另一个道威棱镜设置为0~180°旋转,以接收干涉总光强,并对总光强进行FFT,从而在FFT域中提取OAM态的成分信息.数值仿真结果表明,该方法可有效地实施单个OAM态和复用OAM态的成分检测.不同于传统OAM态的检测方法,本方法可同时获取对FFT域设定子区间内总能量的判决.当该方法被应用于OAM通信系统时,能直接判决各OAM态信息,显著减小系统噪声对OAM复用通信性能的影响.
2. Key Laboratory of Broadband Wireless Communication and Sensor Network Technology, Ministry of Education, Nanjing 210003, China
In order to effectively improve the detection efficiency of orbital angular momentum (OAM), we propose an OAM detection method based on post information processing. In the proposed detection method, a Mach-Zehnder interferometer is applied, and two doves are placed in each arm of the interferometer, where one is setup to 0 degree, and the other is rotated from 0 to 180 degree. The interference beam is received and the fast Fourier transform (FFT) is operated on the received signal. In the FFT domain, each OAM component is separated, named OAM spectrum. Numerical simulation results show that it is separable for one OAM mode, and multiplexed OAM mode by the proposed OAM detection method. Different from the general OAM separation method, the proposed method can obtain the OAM information by summarizing the total energy during a period in FFT domain. And the performance of the communication system can be improved by using this detection method.
光子是信息传递的重要载体,可以通过对光子的强度、相位、频率和偏振等物理量的调制,增加信息传输速率.另一方面,Allen等首次于1992年实验证实了拉盖尔-高斯(LG, Laguerre-Gaussian)模的每个光子具有lħ的轨道角动量(OAM, orbital angular momentum)[1],其中l称为拓扑荷(TC, Topological charge).事实上,轨道角动量是经典力学和量子力学的基本物理量[2],它仅与射线束的空间分布有关,是螺旋相位射线束的自然特性.现已证明,无论是电子束、X-射线、还是无线波束都具有螺旋相位特性[3-11].由于OAM态中l的取值可从负无穷至正无穷[12],且不同拓扑荷的OAM态的空间分布函数(又称空间模)相互正交,因此OAM态更适合于信息的复用传输,现已成为自由空间光通信(FSO, free-space optical communication)系统中一个全新的信息自由度[13-14].
随着OAM的广泛应用,高效快速的OAM检测和分离手段越来越受到人们的关注[15-22]. 2010年,Berkhout等[18-22]提出了一种高效的OAM态检测方法,它基于静态光学原理,运用坐标变换将螺旋相位的光束转变为横向的具有相位梯度的光束,通过在电荷耦合器件横向不同位置的聚焦分离出不同的OAM态.然而,由于每个OAM态在横向位置都存在一定的宽度,其分离精度受到一定限制.
考虑到现实的OAM态通信系统,人们仅需要获取OAM态成分信息,而不需要将接收态逐个分离,同时考虑接收设备的低成本,论文提出一种基于信息后处理的OAM态成分检测方法.它在不需要增加昂贵的物理器件条件下,可通过FFT变换实现OAM态成分检测,且针对一次干涉输出的光强,可通过信息后处理获取各个OAM态的成分信息.
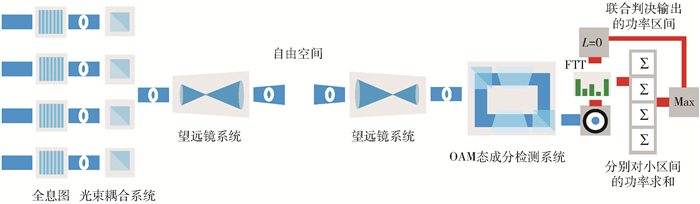
1 基于信息后处理的OAM态成分检测方法基于信息后处理OAM态成分检测方法示意图如图 1所示,马赫-曾德尔干涉仪2臂分别加入一个道威棱镜,其中一个道威棱镜固定放置,即棱镜角度为0°,另一个道威棱镜则以0°~180°为周期绕光轴旋转,因此,光路能够以0°~360°为周期.

|
图 1 基于信息后处理OAM态成分检测方法系统示意图 |
图 1是基于信息后处理OAM态成分检测方法系统示意图.入射的OAM态光束被分束器1分为2路,其中一路光束通过道威棱镜1后(棱镜角度为0°),经由反射镜1射入分束器2;另一路经由反射镜2后,通过一块绕轴旋转的道威棱镜2射入分束器2.接着,2路光束在分束器2处干涉合并,出射光束将由光功率探测器接收,并将数据传送给计算机进行快速傅里叶变换(FFT, fast Fourier transform)处理.最终,计算机将道威棱镜2的旋转情况,给出复用OAM态光束的成分信息.
现给出基于信息后处理OAM态成分检测方法的理论推导.为了简化推导过程,不失一般性,假设OAM态光束的光场分布为
| $ E\left( l \right) = A{\rm{exp}}\;({\rm{i}}l\theta ) $ | (1) |
其中:A是光场强度;l是方位指数,代表OAM态的拓扑荷,θ为方位角. OAM态光束被分成2路,一路经过旋转角度为0的道威棱镜,另一路经过旋转角度为θi/2的道威棱镜.当OAM态经过旋转角度为θi/2的道威棱镜后,其光场分布变为
| $ E\left( l \right) = A{\rm{exp}}\;[{\rm{i}}l(\theta + {\theta _i})] $ | (2) |
2路光束通过相同的光程后在分束器BS2处合并,探测到的光强应为
| $ {\left| {\frac{1}{{\sqrt 2 }}A{\rm{exp}}\;({\rm{i}}l\theta ) + \frac{1}{{\sqrt 2 }}A{\rm{exp}}\;({\rm{i}}l(\theta + {\theta _i}))} \right|^2} $ | (3) |
当方位角旋转一周时,光功率探测器所接收到的光强为
| $ \begin{array}{l} I = \int {{{\left| {\frac{1}{{\sqrt 2 }}A{\rm{exp}}\;({\rm{i}}l\theta ) + \frac{1}{{\sqrt 2 }}A{\rm{exp}}\;({\rm{i}}l(\theta + {\theta _i}))} \right|}^2}} {\rm{d}}\theta = \\ \;\;\;\;\;\;\;\;\;\;\int {{{\left| {\frac{1}{{\sqrt 2 }}A{\rm{exp}}\;({\rm{i}}l\theta )[1 + {\rm{exp}}\;({\rm{i}}l{\theta _i})]} \right|}^2}} {\rm{d}}\theta = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ \mathsf{ π} }}{A^2}(1 + {\rm{cos}}\;l{\theta _i}) \propto 1 + {\rm{cos}}\;l{\theta _i} \end{array} $ | (4) |
由此可见,2路光束干涉后的光场强度I与道威棱镜2旋转角度θi有关,随着lθi的变化成余弦特性,频率与l值有关.对于不同l值,可通过设置θi提取l值的成分信息.
进一步分析复用OAM态情形.假设2个OAM复用态的光场分布为A1exp (il1θ)+A2exp (il2θ),其中l1和l2是2个OAM态的拓扑荷,A1和A2是OAM态光场强度.经过相同的操作后,光功率探测器所接收到的光场强度为
| $ \begin{array}{l} I = \smallint |\left( {1/\sqrt 2 } \right){A_1}{\rm{exp}}\;({\rm{i}}{l_1}\theta )[1 + {\rm{exp}}\;({\rm{i}}{l_1}{\theta _i})] + \\ \left( {1/\sqrt 2 } \right){A_2}{\rm{exp}}\;({\rm{i}}{l_2}\theta )[1 + {\rm{exp}}\;({\rm{i}}{l_2}{\theta _i})]{|^2}{\rm{d}}\theta = \\ \;\;\;A_1^2 + A_2^2 + A_1^2{\rm{cos}}\;({\rm{i}}{l_1}{\theta _i}) + A_2^2{\rm{cos}}\;({\rm{i}}{l_2}{\theta _i}) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{\mathit{k} = 1}^2 {A_k^2} + \sum\limits_{\mathit{k} = 1}^2 {A_k^2} {\rm{cos}}\;({l_k}{\theta _i}) \end{array} $ | (5) |
式(5)表明,光场强度可以表示为2种不同余弦分量的叠加.由此类推,对于n个OAM态复用的光束的光功率探测器所接收到的光强应为
| $ \begin{array}{l} I = \smallint |\left( {1/\sqrt n } \right){A_1}{\rm{exp}}\;({\rm{i}}{l_1}\theta )[1 + {\rm{exp}}\;({\rm{i}}{l_1}{\theta _i})] + \cdots + \\ \;\;\;\;\;\;\left( {1/\sqrt n } \right){A_n}{\rm{exp}}\;({\rm{i}}{l_n}\theta )[1 + {\rm{exp}}\;({\rm{i}}{l_n}{\theta _i})]{|^2}{\rm{d}}\theta = \\ A_1^2 + \cdots + A_n^2 + A_1^2{\rm{cos}}\;({\rm{i}}{l_1}{\theta _i}) + \cdots + A_n^2{\rm{cos}}\;({\rm{i}}{l_n}{\theta _i}) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{\mathit{k} = 1}^2 {A_k^2} + \sum\limits_{\mathit{k} = 1}^2 {A_k^2} {\rm{cos}}\;({l_k}{\theta _i}) \end{array} $ | (6) |
若对式(6)进行快速傅里叶变换,可得到
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{FFT}}\left[ I \right] = \\ 2\sum\limits_{\mathit{k} = 1}^N {A_k^2} {\rm{ \mathsf{ π} }}\mathit{\delta }\left( l \right) + A_1^2{\rm{ \mathsf{ π} }}[\delta (l + {l_1}) + \mathit{\delta }(l - {l_1})] + \\ \;\;\;\;\;\; \cdots + A_N^2{\rm{ \mathsf{ π} }}[\mathit{\delta }(l + {l_N}) + \mathit{\delta }(l - {l_N})] \end{array} $ | (7) |
若仅取式(7)的非负部分,则可以得到
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{FFT}}\left[ I \right] = \\ {\rm{ \mathsf{ π} }}\left[ {2\sum\limits_{\mathit{k} = 1}^N {A_k^2} \mathit{\delta }\left( l \right) + A_1^2\mathit{\delta }(l - {l_1}) + \cdots A_N^2\delta (l - {l_N})} \right] \propto \\ \;\;\;\;2\sum\limits_{\mathit{k} = 1}^N {A_k^2} \mathit{\delta }\left( l \right) + A_1^2\delta (l - {l_1}) + \cdots A_N^2\delta (l - {l_N}) \end{array} $ | (8) |
至此,原本在空间上难以分离的复用OAM态光束,就可以转化成相互分离的δ函数之和,即实现了复用OAM态在FFT域的分离.另一方面,每个OAM本征态分量对应的幅度值正比于各自的功率,因而式(8)也可被理解为描述了接收光束的OAM谱.对于不同l值,可通过设置θi提取l值的OAM态成分信息.于是可在FFT域提取各OAM态.
若将这种OAM态提取方法应用于OAM态复用系统,还具有一定的抗噪声能力.当OAM态受噪声干扰,如大气湍流干扰,在FFT域中会出现OAM态的能量弥散.该方法由于是信息后处理方法,可以在FFT域中设置一段小区域,而不是OAM的本征态能量点,通过小区域间的总能量对OAM态进行判决;同时由式(8)可知,OAM谱在l=0处的幅值可以用来判断所复用的OAM态总个数.
2 成分检测方法在自由空间光通信系统中的应用图 2是基于OAM成分检测的4束OAM态自由空间光通信方案,其中OAM态的拓扑荷值l取2, 4, 6, 8. 4束经过二进制启闭键控(OOK,on-off keying)调制的高斯光入射4个透射型SLM,分别转换成4路不同的OAM态光束,经过光束耦合系统、望远镜系统,传送至自由空间.接收端,复用OAM态光束经过望远镜系统整形后进入OAM成分检测系统.由于数值仿真中最大的OAM值取为8,根据Nyquist采样定理,可以计算出旋转道威棱镜的旋转步进最大值为
|
图 2 基于OAM成分检测的4束OAM自由空间光通信方案 |
对于具体的解复用方案如下:首先在FFT域上划分4个均匀的区间,使得每个区间内都包含一个用于复用传输的OAM本征态;之后,根据获取的OAM谱在l=0处的幅值,判断出此次通信传输的OAM本征态的个数,并分别计算出4个区间内所有OAM态分量的功率之和;最后,依照判断出的OAM本征态的个数,按照区间功率总和从高到低选取相应数目的区间,那么这些区间对应的本征态即判为1,即获得OAM态成分信息.
以Labview软件为数据仿真工具,使用LG模表示OAM态,其中LG模式光的波长设置为1.55×10-6 m,束腰半径设置为0.035 m,光场强度归一化.引入的大气湍流模型采用文献[23]中的相位屏模型.数值仿真中用了10个随机相位屏模拟大气湍流,每2个相位屏之间的距离为100 m,外尺度L0=50 m,内尺度l0=1 mm,LG光束在大气湍流中的传输距离均为1 km.
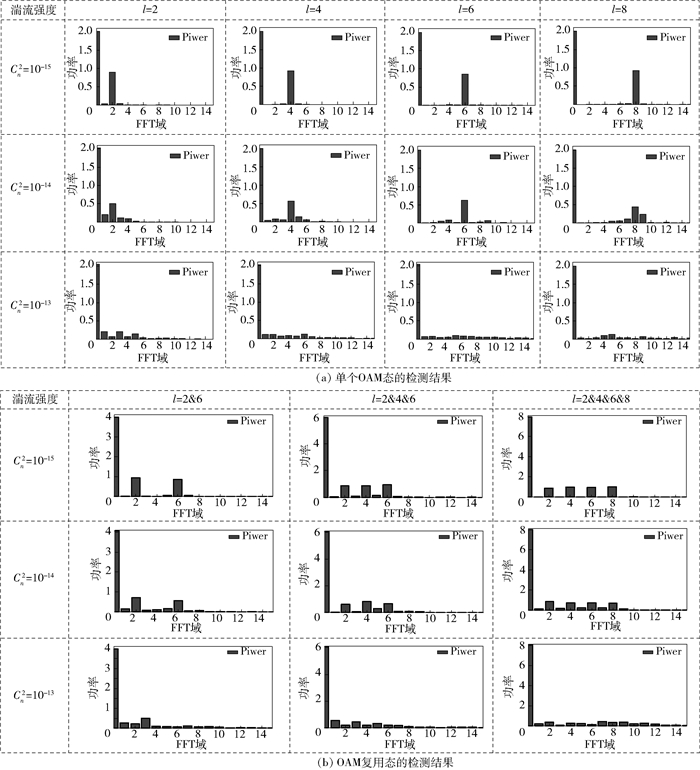
图 3给出了基于FFT的复用OAM态检测方法在不同湍流强度下,对单个OAM态和OAM复用态的检测结果,其中图 3(a)为单个OAM态的检测结果,图 3(b)为OAM复用态的检测结果. 图 3显示不论在何种湍流强度下,FFT域中l=0处的幅值保持不变,且正比于通信过程中总的光功率.因此,在每个OAM本征态光功率相等的前提下,可以凭借OAM谱在l=0处的幅值来判断接收到的OAM态的个数;另一方面,在湍流强度为Cn2=1×10-15 m-2/3和Cn2=1×10-14 m-2/3,即弱湍流和中等强度的湍流,通过该方法可以在FFT域中可以清晰地分析出被检测复用OAM态的成分信息,但是当湍流强度达到Cn2=1×10-13 m-2/3,即强湍流时,OAM谱的弥散现象变得十分严重,无法进行正确判决.研究结果表明基于FFT的复用OAM态检测方法可以在弱或中等强度湍流下检测出单个OAM态和复用OAM态成分. 图 3所示为用同一方法检测单个OAM态和OAM复用态的结果,当输入是单个OAM态时,FFT域有一个OAM谱主峰;而当输入是OAM复用态时,FFT域有多个OAM谱主峰.另外,由于大气湍流的作用,单个OAM态输入时,只有单OAM态在FFT域中弥散,而OAM复用态输入时,在FFT域中不仅存在OAM态的弥散,而且出现OAM态间串扰.因此,基于信息后处理的OAM态成分检测方法应用于单OAM态的精度要优于OAM复用态.
|
图 3 基于信息后处理OAM态检测方法的数值仿真 |
进一步假设l=2, 6, 10, 14,且除了大气湍流外,大气的衰减效应、电信号处理中的噪声由方差为0.01的高斯白噪声模拟. 图 4给出了4OAM态复用通信系统在使用本成分检测方法和基于逆相位掩膜检测方法[24]下的系统误码率性能比较.

|
图 4 l=2, 6, 10, 14的OAM复用通信系统的误码率性能 |
数值仿真结果表明,大气湍流对基于4OAM-DM调制的FSO通信系统有着明显的影响,随着湍流强度的增大,系统的误码率也随之增高;且参与复用的OAM态的l值越大,对应的系统误码率越高.同时,本OAM态成分检测方法相对于逆相位掩膜检测方法有着明显的优势,对于同一l值的OAM态来载荷信息,本OAM态成分检测方法获得的误码率性能至少提升一个数量级,且当复用OAM态的拓扑荷间距越大时,本方法的检测性能越好.例如,利用本OAM态成分检测方法,提取l=2 OAM所载OOK信号时,先获得OAM谱,设置l=1, 2, 3的小区域,对该小区域间的每个OAM谱的能量求和后进行判决.随着OAM态在OAM谱上的距离增大,利用区间功率总和进行判决时,将会大大提高系统误码率性能.当该方法被应用于OAM通信系统时,能直接判决各OAM态信息,显著减小系统噪声对OAM复用通信性能的影响.
3 结束语提出一种基于信息后处理OAM态检测方法,即通过快速傅里叶变换,将空间上具有复杂结构的复用OAM光束转换至FFT域中一个个分离的OAM本征态上,这样可避免空间分离复用OAM态光束所需的复杂设备,且分离过程可以通过计算机的后信息处理完成.数值仿真结果表明:笔者提出的方法可以有效地实施单个OAM态、复用OAM态的成分检测;不同于传统检测方法,只针对某个OAM本征态的能量进行判决,本方法可以获取设定FFT域子区间内总能量的判决.这样,在OAM态通信系统中,当选取区间合理的情况下,可大大减小系统噪声对性能的影响,且直接判断复用OAM态成分信息的解复用方法可为OAM态通信系统的实现提供一种新的思路.
| [1] |
Allen L, Beijersbergen M W, Spreeuw R J, et al. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes[J]. Physical Review a Atomic Molecular and Optical Physics, 1992, 45(11): 81-85. |
| [2] |
Mandel L, Wolf E, Meystre P. Optical coherence and quantum optics[C]//Optical Coherence and Quantum Optics.[S. l.]: Cambridge University Press, 2001: 1438-1439.
|
| [3] |
Franke-Arnold S, Allen L, Padgett M. Advances in optical angular momentum[J]. Laser and Photonics Reviews, 2008, 2(4): 299-313. DOI:10.1002/lpor.200810007 |
| [4] |
Yao A M, Padgett M J. Orbital angular momentum:origins, behavior and applications[J]. Advances in Optics and Photonics, 2011, 3(2): 161-204. DOI:10.1364/AOP.3.000161 |
| [5] |
Uchida M, Tonomura A. Generation of electron beams carrying orbital angular momentum[J]. Nature, 2010, 464(7289): 737-9. DOI:10.1038/nature08904 |
| [6] |
McMorran B J, Agrawal A, Anderson I M, et al. Electron vortex beams with high quanta of orbital angular momentum[J]. Science, 2011, 331(6014): 192-195. DOI:10.1126/science.1198804 |
| [7] |
Sasaki S, McNulty I. Proposal for generating brilliant x-ray beams carrying orbital angular momentum[J]. Physical Review Letters, 2008, 100(12): 124801. DOI:10.1103/PhysRevLett.100.124801 |
| [8] |
Marrucci L, Manzo C, Paparo D. Optical spin-to-orbital angular momentum conversion in inhomogeneous anisotropic media[J]. Physical Review Letters, 2006, 96(16): 163905. DOI:10.1103/PhysRevLett.96.163905 |
| [9] |
Turnbull G A, Robertson D A, Smith G M, et al. The generation of free-space Laguerre-Gaussian modes at millimetre-wave frequencies by use of a spiral phaseplate[J]. Optics communications, 1996, 127(4-6): 183-188. DOI:10.1016/0030-4018(96)00070-3 |
| [10] |
Thidé B, Then H, Sjöholm J, et al. Utilization of photon orbital angular momentum in the low-frequency radio domain[J]. Physical Review Letters, 2007, 99(8): 087701. DOI:10.1103/PhysRevLett.99.087701 |
| [11] |
Tamburini F, Mari E, Sponselli A, et al. Encoding many channels on the same frequency through radio vorticity:first experimental test[J]. New Journal of Physics, 2012, 14(3): 033001. |
| [12] |
Gibson G, Courtial J, Padgett M J, et al. Free-space information transfer using light beams carrying orbital angular momentum[J]. Optics Express, 2004, 12(22): 5448-5456. DOI:10.1364/OPEX.12.005448 |
| [13] |
Wang A, Dong B, Wang D Y, et al. A large serial time-division multiplexed fiber bragg grating sensor network[J]. Journal of Lightwave Technology, 2012, 30(17): 2751-2756. DOI:10.1109/JLT.2012.2205897 |
| [14] |
Wang J, Yang J Y, Fazal I M, et al. Terabit free-space data transmission employing orbital angular momentum multiplexing[J]. Nature Photonics, 2012, 6(7): 488-496. DOI:10.1038/nphoton.2012.138 |
| [15] |
Beijersbergen M W, Coerwinkel R P C, Kristensen M, et al. Helical-wavefront laser beams produced with a spiral phaseplate[J]. Optics Communications, 1994, 112(5-6): 321-327. DOI:10.1016/0030-4018(94)90638-6 |
| [16] |
Heckenberg N R, McDuff R, Smith C P, et al. Generation of optical phase singularities by computer-generated holograms[J]. Optics Letters, 1992, 17(3): 221-223. |
| [17] |
Leach J, Padgett M J, Barnett S M, et al. Measuring the orbital angular momentum of a single photon[J]. Physical Review Letters, 2002, 88(25): 257901. DOI:10.1103/PhysRevLett.88.257901 |
| [18] |
Hossack W J, Darling A M, Dahdouh A. Coordinate transformations with multiple computer-generated optical elements[J]. Journal of Modern Optics, 1987, 34(9): 1235-1250. DOI:10.1080/09500348714551121 |
| [19] |
Lavery M P J, Robertson D J, Berkhout G C G, et al. Refractive elements for the measurement of the orbital angular momentum of a single photon[J]. Optics Express, 2012, 20(3): 2110-2115. DOI:10.1364/OE.20.002110 |
| [20] |
Berkhout G C G, Lavery M P J, Courtial J, et al. Efficient sorting of orbital angular momentum states of light[J]. Physical Review Letters, 2010, 105(15): 153601. DOI:10.1103/PhysRevLett.105.153601 |
| [21] |
Mirhosseini M, Malik M, Shi Z, et al. Efficient separation of the orbital angular momentum eigenstates of light[J]. Nature Communications, 2013, 4(7): 2781. |
| [22] |
Cheng Li, Shengmei Zhao. Efficient separating orbital angular momentum mode with radial varying phase[J]. Photonic Research, 2017, 5(4): 267-270. |
| [23] |
Zhao S M, Leach J, Gong L Y, et al. Aberration corrections for free-space optical communications in atmosphere turbulence using orbital angular momentum states[J]. Optics Express, 2012, 20(1): 452-461. DOI:10.1364/OE.20.000452 |
| [24] |
Willner A E, Huang H, Yan Y, et al. Optical communications using orbital angular momentum beams[J]. Advances in Optics and Photonics, 2015, 7(1): 66-106. DOI:10.1364/AOP.7.000066 |


