为更全面地反映用户个人偏好,提高推荐的准确度,提出了一种融合多源异构数据的混合推荐模型.综合考虑了用户社交关系和用户评论对用户评分的影响,从评论中提取主题信息作为用户和商家的特征,采用社区发现算法为用户划分社区,利用机器学习方法为社区建立模型,预测用户对商家的评分,再根据评分对商家进行排序,取前N个商家推荐给用户.实验结果表明,提出的混合推荐模型与经典推荐算法相比,可提高评分预测的准确度,从而提高推荐的准确度.
In order to reflect users' personalized preferences more comprehensively and improve the accuracy of recommendation, a hybrid recommendation model based on fusion of multi-source heterogeneous data is proposed. This model takes the impacts from both users' social relationships and reviews on ratings into account. Topics are extracted from reviews as user features and business features, and then communities are divided for users via a community discovery algorithm. Finally, a machine learning algorithm is used to model user communities in order to predict ratings. Businesses are ranked based on predicted ratings and then the top N businesses are recommended to the user. The experimental results show that the proposed hybrid recommendation model can improve the rating prediction accuracy and recommendation accuracy compared with the conventional recommendation algorithms.
为解决互联网信息过载问题,使用户更迅速地获取感兴趣的信息,推荐系统被广泛应用于电子商务、新闻资讯、电影和音乐等网站.为充分利用多源异构数据优势,更好地挖掘用户偏好和商家属性,从而提高推荐系统精确度,笔者提出了一个混合推荐模型,该模型可根据新用户的社交关系数据为其划分社区,解决推荐系统的冷启动问题.
1 相关工作早期的基于评分的推荐算法主要有协同过滤推荐算法[1-2]和基于模型的推荐算法.基于模型的推荐算法中,基于矩阵分解的推荐算法应用最为广泛.为提高基于评分数据的推荐准确度,近年来有学者将神经网络和矩阵分解相结合,提出神经网络矩阵分解(NNMF, neural network matrix factorization)[3];将神经网络与协同过滤相结合提出神经协同过滤(NCF, neural collaborative filtering)[4].基于评分数据的推荐只采用用户的评分数据,推荐结果缺乏可解释性,对于稀疏数据集推荐准确度较低.
为解决基于评分数据推荐算法的准确度较低和缺乏可解释性的问题,用户评论数据被引入推荐算法,主要有4种方案. 1)提取文本话题信息. Xu和Zuo[5]利用话题模型分析项目申请书中文本信息和专家属性信息,计算专家和项目间的匹配度进行推荐. Mcauley和Leskovec[6]将隐因子模型和隐狄利克雷模型结合以分析评论和评分数据. 2)基于特征词库分析文本信息. Takuma[7]根据用户的评论数据为用户建立偏好词典,并表示用户特征,依据用户偏好的相似度为用户做推荐. Zhang等[8]提出显式因子模型,将显式因子和隐式因子结合以提高推荐系统的准确度,利用提取的特征词解释推荐结果,以提高推荐系统的可解释性. 3)通过文本聚类进行推荐. Xu等[9]通过文本信息确定用户社区和物品类别,基于用户社区和物品类别进行推荐以提高推荐的准确度. 4)基于深度学习的表示学习.深度学习获取的非线性特征表示可更好地描述用户和物品的特征[10].基于评论数据的推荐算法会遇到数据稀疏问题,因为每种方案都需要大量的用户评论对模型进行训练.
基于“用户更信任朋友的推荐而不是陌生人的推荐”的事实,社交网络被引入推荐系统中. Jamali和Ester[11]考虑直接朋友对用户特征因子的影响,将信任传播模型和矩阵分解模型结合,以提高传统矩阵分解模型的准确度. Ma等[12]将概率矩阵分解,与信任网络结合,该模型的计算时间随评分数据的增加而线性增加. TrustSVD[13]是基于SVD++的矩阵分解模型,考虑显式反馈和隐式反馈,通过结合社交信息提高推荐准确度. Deng等[14]将深度学习模型与矩阵分解结合,处理用户评分、社交关系数据.结合社交关系数据进行推荐可提升推荐系统在稀疏数据集上的准确度,并解决冷启动问题.
目前,将社交关系、评分、评论数据结合进行推荐的模型少,且存在问题. Ma和Che[15]提出融合社交网络和评论信息的协同过滤模型,由于协同过滤算法严重依赖好友评分,对于稀疏数据需要寻找间接好友,算法复杂度较高且准确度下降明显.基于多源数据混合推荐的深度学习模型[16]目前主要将基于内容的推荐方法和协同过滤方法组合.融合社交关系、评论和评分数据的深度学习模型尚未提出.
为利用多源异构数据优势以提高推荐准确度并解决冷启动问题,笔者提出了一种混合推荐模型.
2 融合社交关系和用户评价的推荐评分数据简单明确、评论数据信息丰富、社交关系数据反映用户之间的信任关系,三类数据各具优势,融合三类数据进行推荐显然会提高推荐准确度、解决冷启动问题.笔者提出的融合三类数据的混合推荐模型如图 1所示.模型采用社区发现算法为用户划分社区,以社区用户评论特征为基础训练用户社区回归模型,使用主题模型提取用户和商家特征.由于同社区用户的推荐模型相同,评论极少的用户只要通过社区划分确定其所属社区,就可用训练好的社区模型参数近似表示该用户的话题权重,使得评分预测更为准确.对于没有消费行为但存在于老用户社交关系中的新用户,通过确定其所属社区并利用相应社区模型进行推荐,从而解决冷启动问题.此外,模型还提高了稀疏数据集推荐准确度,与协同过滤算法相比,避免海量用户之间的相似度计算,大大降低了计算的时间和空间复杂度.
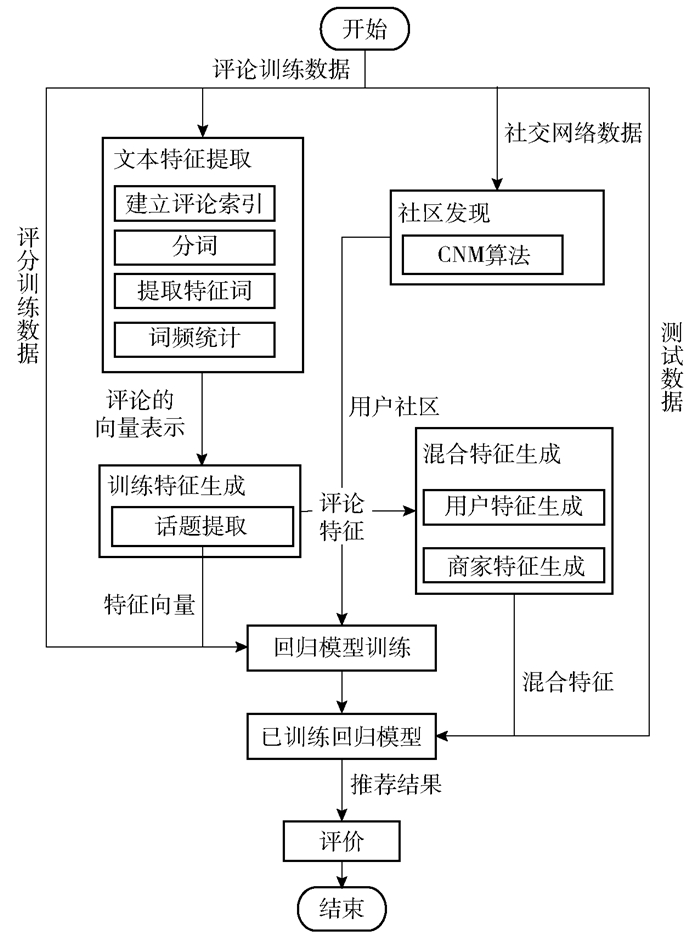
|
图 1 混合推荐模型推荐流程 |
1) 训练阶段:通过话题聚类方法提取训练集中每条评论的特征信息.同时,应用社区发现算法分析社交关系数据确定训练集的用户社区.结合回归模型,将社区内用户的评论特征作为输入,对商家评分作为标签,训练社区回归模型.
2) 预测阶段:用户和商家的每条评论特征叠加构成用户和商家的个体特征.将测试集中用户和商家的混合特征输入回归模型预测评分.
3) 评价阶段:计算预测评分与测试数据集中实际评分的均方根误差评价预测评分结果.
2.1 文本特征提取为提取评论中的文本话题特征,需要对文本进行预处理,包括建立评论索引、分词、提取特征词、词频统计4个步骤.第1步,将用户和商家的ID转换为数字,以索引用户对商家的评论,为生成用户、商家特征做准备;第2步,对评论文本进行分词,将评论文本转换为一个字符串数组;第3步,去除字符串数组中的标点符号、the、a等无意义且频繁出现的停止词;第4步,计算词频并删除重复出现的词语,将词语数组转换为向量,作为话题模型的输入.
2.2 话题提取隐狄利克雷分配(LDA,latent dirichlet allocation)模型是一种常用的话题模型,广泛应用于信息检索和自然语言处理.
假设有评论文档M篇,共包含词语N个,以此为输入训练LDA模型.训练过程中,由初始的狄利克雷分布α与β分别随机采样出一个文档m中的话题分布θm和话题tm, n的词频φk,根据已计算的文档m中词n的词频ωm, n,通过极大似然估计法更新参数α和β,即最大化对数似然:
| $ L(\alpha ,\beta ) = \sum\limits_m {\ln }\; p\left( {{\omega _m}|\alpha ,\beta } \right) $ | (1) |
训练完成后,每段评论都将转换为设定话题数的向量形式:
| $ {\mathit{\boldsymbol{\theta }}_{ui1}} = \left( {{\theta _{ui}}, \cdots ,{\theta _{uik}}} \right),k \in \{ 1, \cdots ,K\} $ | (2) |
其中:θui表示用户u对商家i评论,为K维向量;K为人工设置的话题数量;θuik为用户u对商家i的评论中出现话题k的概率.
为加快LDA参数求解速度,在线变分贝叶斯算法被提出[17],此算法执行效率高,实现难度低,并可在分布式环境下执行.本模型采用此算法.
2.3 社区发现算法基于模块度概念,Clauset、Newman和Moore提出在巨大网络上快速寻找社区的算法CNM[18].通过最大化模块度Q确定用户的最优社区:
| $ Q = \sum\limits_i {\left( {{e_{ii}} - a_i^2} \right)} $ | (3) |
其中:eii为社区i中内部边数占总边数的比例,ai为社区i中与外部节点相连的边数占总边数的比例.社区内部边数占比越高,和外部相连的边数占比越低,模块度越大.当模块度达到最大值时,社区划分结果最优.
| $ {e_{ij}} = \frac{1}{{2l}}\sum\limits_{vw} {{A_{vw}}} \delta \left( {{c_v},i} \right)\delta \left( {{c_w},j} \right) $ | (4) |
| $ {a_i} = \frac{1}{{2l}}\sum\limits_v {{d_v}} \delta \left( {{c_v},i} \right) $ | (5) |
其中:eij为社区i中节点与社区j中节点之间的边数占总边数的比例,l表示边的总数,Avw的取值表示节点v和节点w是否相连,若相连则取1;否则取0. dv表示和节点v相连的边数,cv为v节点所属的社区,δ方法用来判断输入是否属于同一社区,如果是输出1;否则,输出0.
为得到模块度的最大值,需要计算模块度增量:
| $ \Delta {Q_{ij}} = 2\left( {{e_{ij}} - {a_i}{a_j}} \right) $ | (6) |
其中ΔQij代表合并社区i和j模块度的变化.求解Q的具体步骤如下:
1) 计算有连接的社区之间模块度增量ΔQij;
2) 合并模块度增量最大的2个社区,并更新ΔQij和Q.
重复以上步骤直到模块度Q不再增加为止. CNM算法将社交网络中的用户划分为多个社区,为各社区的用户分别建立预测模型.
2.4 特征生成LDA模型训练完成后,每条评论特征向量每个维度所代表的话题一一对应,评论特征向量的叠加和归一化操作可以得到多条评论的总体特征,所以用户评论的总体特征可以用来代表用户的特征,商家收到的所有评论的总体特征可以用来代表商家的特征.
模型将用户所有评论的特征向量相加并归一化以计算用户特征因子:
| $ p_{uk}^\prime = \frac{{\sum\limits_i {{\theta _{uik}}} }}{{{D_u}}} $ | (7) |
| $ {p_{uk}} = \frac{{p_{uk}^\prime }}{{\sum\limits_k {p_{uk}^\prime } }},k \in \{ 1,2, \cdots ,K\} $ | (8) |
其中:Du为用户u所有的评论数,p′uk为用户在话题k上的总概率,puk为其归一化的表示.用户u的特征因子为
| $ {\mathit{\boldsymbol{p}}_u} = \left( {{p_{u1}}, \cdots ,{p_{uK}}} \right) $ | (9) |
用户特征因子维数和话题模型中设置的话题数相同,都为K.类似地,可计算出商家的特征因子:
| $ {\mathit{\boldsymbol{q}}_i} = \left( {{q_{i1}}, \cdots ,{q_{iK}}} \right) $ | (10) |
用户特征因子的各维度值大小为用户对每个话题的关注程度,用户对某个话题越关注,特征因子中该话题维度值越大.类似地,一个商家在某话题被评论越多,商家在该话题维度值越大.将用户所有的评论特征向量相加,则得到代表用户特征的向量,将商家收到的评论的特征向量相加,可生成代表商家特征的向量.
2.5 回归模型用户社区确定后,以社区中用户评论的特征向量为输入,评分为标签训练社区回归模型.线性回归模型的惩罚函数有多种,本文实验(见3.2.1节)对比了不同回归模型的预测结果.后续实验结果表明,采用L2惩罚函数的线性回归模型(L2LR, l2-norm linear regression)预测准确度最高,因此选用L2LR作为基本模型.评分和评论特征向量的线性关系可表示为
| $ {r_{u\dot i}} = {\mathit{\boldsymbol{W}}^{\rm{T}}}{\mathit{\boldsymbol{\theta }}_{ui}} + {\varepsilon _c} $ | (11) |
其中:W=(W1, …, WK)为话题的权重向量,代表每个话题的重要程度;
| $ \mathop {\rm{argmin}}\limits_{\mathit{\boldsymbol{W}},\varepsilon } \sum\limits_C {\sum\limits_{\nu \in C,i} {{{\left( {\mathit{\boldsymbol{W}}_C^{\rm{T}}{\mathit{\boldsymbol{\theta }}_{ui}} + {\varepsilon _C} - {r_{ui}}} \right)}^2}} } + \lambda {\left\| {{\mathit{\boldsymbol{W}}_C}} \right\|^2} $ | (12) |
其中:ε为偏差;C代表社区;λ为惩罚参数;‖WC‖2为L2惩罚函数,能增强模型的泛化能力,防止过拟合.
为各社区分别建立线性回归模型,可得到N个具有不同权重和偏差的社区线性回归模型:
| $ {r_{u\dot i}} = \left\{ \begin{array}{l} \mathit{\boldsymbol{W}}_{{C_1}}^{\rm{T}}{\mathit{\boldsymbol{\theta }}_{ui}} + {\varepsilon _{{C_1}}},\;\;\;\;u \in {C_1}\\ \mathit{\boldsymbol{W}}_{{C_2}}^{\rm{T}}{\mathit{\boldsymbol{\theta }}_{ui}} + {\varepsilon _{{C_2}}},\;\;\;\;u \in {C_2}\\ \;\;\;\; \cdots \\ \mathit{\boldsymbol{W}}_{{C_N}}^{\rm{T}}{\mathit{\boldsymbol{\theta }}_{ui}} + {\varepsilon _{{C_N}}},\;\;\;\;u \in {C_N} \end{array} \right. $ | (13) |
为预测用户对某商家的评分,将用户和商家特征因子相乘得到混合特征并归一化:
| $ \theta _{uik}^\prime = {p_{uk}}{q_{ik}} $ | (14) |
| $ {{\hat \theta }_{uik}} = \frac{{\theta _{uik}^\prime }}{{\sum\limits_k {\theta _{uik}^\prime } }},k \in \{ 1,2, \cdots ,K\} $ | (15) |
首先计算用户和商家的混合特征θ′uik,归一化得到
| $ {{\hat r}_{u\dot i}} = \mathit{\boldsymbol{W}}_C^{\rm{T}}{{\mathit{\boldsymbol{\hat \theta }}}_{u\dot i}} + {\varepsilon _C},u \in C $ | (16) |
若用户和商家某话题的概率都比较高,相乘得到更高概率;反之则概率较低,如此可计算用户和不同商家之间的混合特征.通过用户所属社区的线性回归模型,预测用户对商家的评分,根据评分对商家进行排序,取前N个商家作为推荐结果推荐给用户.
3 实验评估为进行算法选型以及评价所提出的混合推荐模型,设计了3组对比实验,实验数据集采用Yelp公开数据集.实验运行环境为Spark2.2.0分布式集群计算环境,集群操作系统为Ubuntu16.04,集群由6个节点组成,其中主节点1个,工作节点5个.每个节点具有四核八线程CPU、500 GB硬盘、16 GB内存.
笔者提出的混合推荐模型采用LDA、L2LR、CNM算法,模型简称为LLC模型.
3.1 实验数据集实验采用2016年发布的Yelp数据集,其中用户686 556位、商家85 539个、评论2 085 066条.
实验以用户评论数大于5、10、20为过滤条件,将数据集划分为3个不同稀疏度的数据集,如表 1所示.针对每个数据集,随机选取80%的数据作为训练集,余下20%的数据作为测试集,并确保训练集中的用户未评论过测试集中的商家.
|
|
表 1 数据集划分信息 |
共设计3组实验:实验1,对比线性模型与其他回归模型的评分预测准确度;实验2,计算社交关系数据对线性模型预测准确度的影响;实验3,对比LLC模型与其他代表性推荐算法的评分预测准确度,证明笔者所提出的LLC模型可提高评分预测准确度.
3.2.1 实验1:回归模型对比通过实验对比不同回归模型的评分预测准确度,以选择最优的回归模型对Yelp1、Yelp2和Yelp3数据集进行处理.实验采用LDA分析评论数据并提取特征,以评论特征向量为输入,对比采用L1惩罚函数的线性回归模型L1LR(惩罚参数设置为0.1),采用L2惩罚函数的线性回归模型L2LR(惩罚参数设置为0.3)、基于弹性网络(regularization and variable selection)惩罚函数的线性回归模型ElasticNetLR(弹性网络参数设置为0.8,惩罚参数设置为0.1)、随机森林回归模型(RFR,random forest regression)(树的棵数设置为100)、梯度提升树回归模型(GBTR,gradient-boosted tree regression).
如表 2所示,实验以均方根误差(RMSE,root mean square error)作为评价指标(RMSE值越低准确度越高),其中黑体表示每行中精确度最高的值.将3个数据集话题数分别设置为10、30和50,对比5种回归模型的准确度.实验结果表明,线性模型大多数情况下准确度优于RFR和GBTR.线性模型中,数据集为Yelp2、话题数为10的情况下,RFR的准确度较高,其他情况L2LR模型的RMSE均低于其他回归模型,即准确度更高.因此,笔者所提出推荐模型采用L2LR.
|
|
表 2 回归算法对比 |
为证明社交关系数据对评分预测的正面影响,本节实验对比添加社交网络信息的L2LR+CNM模型和未添加社交关系数据的L2LR模型的准确度,实验采用3个数据集.实验结果如图 2所示,对于3个数据集,添加社交关系数据后评分预测准确度均有所提高. 图 2中横坐标的因子数即为设置的话题数.
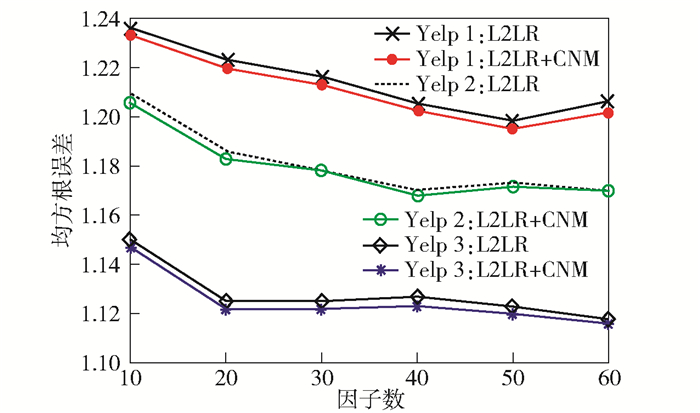
|
图 2 添加社区信息前后准确度对比 |
本节实验将所提出的LLC模型与经典的协同过滤算法、融合社交网络的推荐算法进行对比.对比算法如下.
1) SVD++:基于SVD的改进算法,考虑用户的隐式反馈.学习率设置0.01,最大迭代次数设置100,用户的正则化参数设置0.2,物品的正则化参数设置0.2.
2) UserKNN:基于用户的协同过滤算法.邻居数设为50.
3) ItemKNN:基于物品的协同过滤算法.邻居数设为50.
4) TrustSVD:一种考虑好友关系、显式反馈和隐式反馈的推荐模型[15].学习率设置0.000 1,最大迭代次数设置50,用户的正则化参数设置1.2,物品的正则化参数设置1.2,社交网络的正则化参数设置0.9,误差的正则化参数设置1.2,衰减参数设置1.0.
实验对比不同特征因子数量下各模型的准确度,实验结果如表 3所示.其中UserKNN与ItemKNN的准确度与特征因子数量无关,所以保持不变;其他算法准确度均受特征因子数量影响,因子数增加时,LLC模型和SVD++模型准确度升高,TrustSVD模型的准确度基本不变;数据集为Yelp2、特征因子数为25时,SVD++模型和LLC模型准确度一致;其他情况,LLC模型准确度最高.总体来说,LLC模型比其他推荐算法准确度更高,且随特征因子数增加准确度有升高趋势.
|
|
表 3 混合推荐模型与其他算法对比 |
所提出的模型融合社交关系和用户评分评论数据进行推荐,引入话题模型和社区发现算法获取用户偏好和商家特征,可提高推荐的准确度,解决冷启动问题.通过对评论数据进行话题提取,可提高评分也即推荐结果的可解释性,使用户更易理解和接受.实验结果表明,模型在不同稀疏度数据集上的表现均优于所对比算法.
| [1] |
王永, 邓江洲. 基于KL散度的用户相似性协同过滤算法[J]. 北京邮电大学学报, 2017, 40(2): 110-114. Wang Yong, Deng Jiangzhou. User similarity collaborative filtering algorithm based on KL divergence[J]. Journal of Beijing University of Posts and Telecommunications, 2017, 40(2): 110-114. |
| [2] |
王晓军, 付超. 利用模糊分块改进协同过滤的扩展性和准确性[J]. 北京邮电大学学报, 2017, 40(1): 74-78. Wang Xiaojun, Fu Chao. Enhancing scalability and accuracy of collaborative filtering using fuzzy blocking[J]. Journal of Beijing University of Posts and Telecommunications, 2017, 40(1): 74-78. |
| [3] |
Dziugaite G K, Roy D M. Neural network matrix factorization[EB/OL]. (2015-12-10). https://arxiv.org/abs/1511.06443.
|
| [4] |
He Xiangnan, Liao Lizi, Zhang Hanwang, et al. Neural collaborative filtering[C]//WWW'17 Proceedings of the 26th International Conference on World Wide Web. New York: ACM, 2017: 173-182.
|
| [5] |
Xu Yunhong, Zuo Xianli. A LDA model based text-mining method to recommend reviewer for proposal of research project selection[C]//International Conference on Service Systems and Service Management. New York: IEEE, 2016: 1-5.
|
| [6] |
Mcauley J, Leskovec J. Hidden factors and hidden topics: understanding rating dimensions with review text[C]//Proceedings of the 7th ACM Conference on Recommender System. New York: ACM, 2013: 165-172.
|
| [7] |
Takuma K, Yamamoto J, Kamei S, et al. A hotel recommendation system based on reviews: what do you attach importance to?[C]//International Symposium on Computing and Networking. New York: IEEE, 2016: 710-712.
|
| [8] |
Zhang Yongfeng, Lai Guokun, Zhang Min, et al. Explicit factor models for explainable recommendation based on phrase-level sentiment analysis[C]//Proceedings of the 37th International ACM SIGIR Conference on Research and Development in Information Retrieval. New York: ACM, 2014: 83-92.
|
| [9] |
Xu Yinqing, Lam W, Lin Tianyi. Collaborative filtering incorporating review text and co-clusters of hidden user communities and item groups[C]//Proceedings of the 23rd ACM International Conference on Conference on Information and Knowledge Management. New York: ACM, 2014: 251-260.
|
| [10] |
Shen Xiaoxuan, Yi Baolin, Zhang Zhaoli, et al. Automatic recommendation technology for learning resources with convolutional neural network[C]//International Symposium on Educational Technology. New York: IEEE, 2016: 30-34.
|
| [11] |
Jamali M, Ester M. A matrix factorization technique with trust propagation for recommendation in social networks[C]//Proceedings of the fourth ACM conference on Recommender Systems. New York: ACM, 2010: 135-142.
|
| [12] |
Ma Hao, Yang Haixuan, Lyu M R, et al. SoRec: social recommendation using probabilistic matrix factorization[C]//Proceedings of the 17th ACM Conference on Information and Knowledge Management. New York: ACM, 2008: 931-940.
|
| [13] |
Guo Guibing, Zhang Jie, Yorke-Smith N. TrustSVD: collaborative filtering with both the explicit and implicit influence of user trust and of item ratings[C]//Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence. New York: ACM, 2015: 123-129.
|
| [14] |
Deng Shuiguang, Huang Longtao, Xu Guandong, et al. On deep learning for trust-aware recommendations in social networks[J]. IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(5): 1164-1177. DOI:10.1109/TNNLS.2016.2514368 |
| [15] |
Ma Haojie, Che Ddongsheng. An integrative social network and review content based recommender system[J]. Journal of Industrial and Intelligent Information, 2016, 4(1): 69-75. |
| [16] |
黄立威, 江碧涛, 吕守业, 等. 基于深度学习的推荐系统研究综述[J]. 计算机学报, 2018, 41(7): 191-219. Huang Liwei, Jiang Bitao, Lu Shouye, et al. Survey on deep learning based recommender systems[J]. Chinese Journal of Computers, 2018, 41(7): 191-219. |
| [17] |
Hoffman M D, blei D M, Bach B. Online learning for latent dirichlet allocation[C]//International Conference on Neural Information Processing Systems. Berlin: Springer, 2010: 856-864.
|
| [18] |
Clauset A, Newman M E J, Moore C. Finding community structure in very large networks[J]. Physical Review E, 2004, 70(6 Pt 2): 066111. |


