在网络边缘节点上部署服务设施能够有效降低响应时延与链路带宽需求，在雾计算和第5代移动通信系统(5G)中有着广泛的应用^[1-2].这时，一个很自然的问题是，在哪些节点上部署数目有限的服务设施能够使性能达到最优，这也被称作服务设施放置问题，其典型数学模型是使整体性能或平均性能达到最优的p-中点问题(p-median problem).已经证明，在一般网络拓扑中，p-中点问题是NP-Hard的^[3-4].而针对这一问题的求解算法主要为以下3类：特殊拓扑下的放置算法^[5]、有效的启发式算法^[6]以及各种近似算法^[7].例如，Lorena等^[8]提出了一种基于遗传算法的启发式方法.笔者研究了p-中点问题的一个扩展版本，即(p+m)-中点问题，是指在不改变网络中已有m个预置服务节点位置的前提下如何向网络中继续引入p个扩展服务节点，并使新引入服务节点的总效用达到最大.在此基础之上，提出了一种基于贪婪策略与禁忌搜索策略相结合启发式服务设施放置算法.与现有结果相比，提出的算法适用一般拓扑网络，在性能与复杂度方面也具有充分优势.

1 问题描述

令G=(V, E)表示所研究的图状网络.其中，V为网络节点的集合，E为边的集合.不失一般性，假设G是一个简单联通图.进一步，(p+m)-中点问题涉及2种类型的服务节点：m个位置不可变更的预置服务节点以及p个位置可自由改变的扩展服务节点.称与请求用户(或设备)直接相连的网络节点为请求节点，称每个请求节点所连接的用户数目为该节点的需求.针对每个用户的服务响应，假设不同链路所消耗的通信成本是无差别的.基于最小化总的成本方面的考虑，假设任意节点对都将选择节点间链路跳数最小的路径进行通信，并称这一跳数为节点对间的距离.当节点间存在多条最短路径时，从中随机选取一条作为通信链路，将不会影响得到的性能结果.

在此基础之上，总的通信成本被定义为经需求加权后请求节点与响应节点之间的距离之和，引入扩展服务节点的目的在于降低该总成本，并称这种成本上的降低为服务设施产生的效用.经推导可得，每个扩展服务设施的效用可以表示为

$ {r_j} = \sum\limits_i {{a_i}({{\tilde d}_i} - {d_{ij}}){x_{ij}}} $

其中：i表示请求节点，j表示服务节点，d_ij表示节点i, j间的距离，${{\mathit{\tilde d}}_{\mathit{ij}}}$表示在只存在预置服务节点情况下请求节点i到指派给自身的服务节点间的距离，x_ij指示节点i, j间的指派关系.更具体地，x_ij=1表示服务节点i被指派给请求节点j；而x_ij=0表示服务节点i未指派给请求节点j.加总所有扩展服务节点的效用，可得总效用为

$ R = \sum\limits_j {{r_j}} $

这时，成本最小化问题将被转换为如下效用最大化问题

$ \begin{array}{l} \;\;\;\;\;\;\;\;\;{\rm{max}}\;R\\ {\rm{s}}{\rm{.t}}{\rm{.}}\left\{ \begin{array}{l} \sum {x_{ij}} = 1\\ {x_{ij}} \le {y_j}\\ \sum {y_j} = p + m\\ {x_{ij}}, {y_j} \in \left\{ {0, 1} \right\} \end{array} \right. \end{array} $

其中：y_j表示节点j的服务设施配置状态，是问题的决策变量. y_j=1表示节点j是一个服务节点，相反，y_j=0表示该节点不是一个服务节点.

2 服务设施放置算法

所提出的基于禁忌搜索策略的启发式服务设施放置算法以迭代方式来增添网络中的服务节点数目，每次迭代将进一步被分解成2个阶段：(扩展)服务节点添加阶段以及放置模式调整阶段.前一阶段是指向网络中引入一个新的服务设施，并将其放置于在不改变所有现有服务节点位置前提下使总效用R达到最大的节点上，这种方式显然是基于贪婪式策略的.放置模式调整阶段依然以迭代方式来实现，借助禁忌搜索策略的放置模式进行微调，以进一步提高扩展服务节点所产生的总效用.

在所提出的算法中，禁忌搜索策略的实现建立在“搜索域(search domain)”这一概念之上的，而搜索域则是指以某个服务节点为中心的节点子集.令S_j表示以服务节点j为中心的搜索域，那么它将是由下列条件所确定的集合：

1) j∈S_j

2) 当i≠j时，i∈S_j当且仅当

$ \left\{ \begin{array}{l} {y_i} = 0\\ {d_{ij}} \le r\\ i, j之间最短路径上不存在除j之外的服务节点 \end{array} \right. $

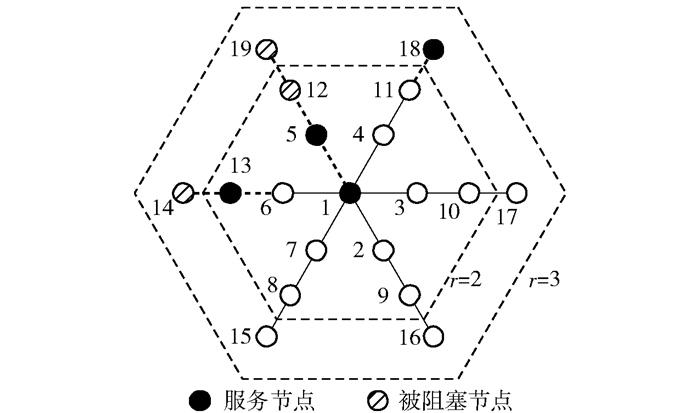
这里，条件2)中的r被称作搜索半径，是一取值为正的常量.条件2)中第3个分支所排除的节点被称为由其他服务节点所阻塞的节点，而这种现象被称作是非中心服务节点的阻塞效应. 图 1显示以服务节点1为中心不同搜索半径下的搜索域，用于对搜索域这一概念进行简要解释.当r=2时，搜索域为{1, 2, 3, 4, 6, 7, 8, 9, 10, 11}.其中，节点5和13是异于搜索域中心的其他服务节点，节点12被服务节点5所阻塞.类似地，r=3时的搜索域为{1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 15, 16, 17}.

基于上述论述，放置模式调整阶段内的每次迭代可以描述如下.

1) 对于每个扩展服务节点，在以自身为中心的搜索域内为中心节点上的服务设施找到一个最佳候选置换位置，使得在不改变其他扩展服务节点位置的前提下，将搜索域中心节点上的服务设施移动到被选定的最佳候选节点位置时的总效用大于将该服务设施放置在搜索域内的其他节点位置时的总效用.

2) 如果步骤1)中所有服务设施在放置位置上的移动都不能使总效用获得一个正向增量，那么退出放置模式调整阶段.否则，选出那个能使总效用增量达到最大的扩展服务节点以及相关联的放置位置调整方式.

3) 执行由步骤2)所确定出的关于服务设施在放置位置的调整.

4) 返回步骤1)，重复执行上述步骤.

最终，表 1列举了算法伪码描述以及性能分析中将会用到的符号和表示，算法1正式描述了所提出的算法.

算法1    基于禁忌搜索策略服务设施放置算法

输入：

1    网络拓扑，需求配置，预置服务节点

2    γ←0

服务节点添加阶段：

3    γ←γ+1

4    ${{\tilde R}^{(0)}} \leftarrow \mathop {{\rm{max}}}\limits_{j \in V} R\left( {\gamma {\rm{ }} \mapsto j} \right)$(计算以贪婪策略引入一个新的服务设施时的总效用)

5    $\mathit{\ell} \gamma \leftarrow {\rm{arg}}\mathop {{\rm{max}}}\limits_{j \in V} \mathit{R}\left( {\gamma \mapsto j} \right)$(返回能达到这一总效用服务设施的放置位置)

6    ${y_{\mathit{\ell} \gamma }} \leftarrow 1$

7    m←0

放置模式调整阶段：

8    m←m+1

9    for all j∈V_R-free do

10            y_j←0

11            ${\tilde R_j^{(m)}}\;\; \leftarrow \mathop {{\rm{max}}}\limits_{s \in {S_j}} R\left( {j \to s} \right)$

12            $\mathit{\ell} j \leftarrow {\rm{arg}}\mathop {{\rm{max}}}\limits_{s \in {S_j}} \tilde R\left( {j \to s} \right)$(寻找与指定服务节点相对应的置换节点)

13            ${y_{\mathit{\ell} j}} \leftarrow 1$

14      ${{\tilde R}^{(m)}} \leftarrow \mathop {{\rm{max}}}\limits_k {\tilde R_k^{(m)}}$

15      ${\rm{if}}\;{{\tilde R}^{(m - 1)}}{\tilde R_k^{(m)}}\;\;\;{\rm{then}}$

16            $j \leftarrow {\rm{arg}}\;\mathop {{\rm{max}}}\limits_k {\tilde R_k^{(m)}}$ (确定最优置换节点)

17            y_j←0

18            ${y_{\mathit{\ell} j}} \leftarrow 1$

19             for all j∈V_R-free do

20                  if R_j=0 then (重新放置处理过程中出现的空闲扩展服务设施)

21                        y_j←0

22                        γ←γ－1

23    else

24          go to Line 8

输出：

25    $R\left( \gamma \right) \leftarrow {{\tilde R}^{(m - 1)}}$

26    go to Line 3 until γ=p

3 性能分析

首先给出算法1的一个性质，接下来对算法复杂度进行分析.

定理  假设网络规模有限.当γ=p时，执行算法1能够使扩展服务设施全部被放置在请求节点上，此时的服务设施放置模式是理论最优的.

证明

1) 对任意j∈V_R-free，当|V_{Q, j}|=1时，考虑在从j到V_{Q, j}中唯一请求节点之间的最短路径上的所有节点.假设这些节点中的每一个都有可能成为一个单独服务节点，那么距离请求节点越近，服务节点的效用也就越大.按照这一原理，模式调整阶段将会使位于节点j上的服务设施最终移动到V_{Q, j}中唯一的请求节点位置上，这一请求节点将成为能为自身服务的节点.

2) 由算法的第19~22行可知，V_R-free不包含效用为0的服务节点，意味着对任意j∈V_R-free，V_{Q, j}非空.因此，当p=|V_Q|时，每个V_{Q, j}只能包含一个请求节点.按照(1)的结论，这些请求节点同时也将成为服务节点.

3) 当每个请求节点上的需求都能被其自身的服务设施服务响应时，针对所有需求的通信成本都是最小的，这时总的通信成本将达到理论上的最优，且没必要再增添更多的扩展服务设施□

对算法1的时间复杂度分析相对复杂，需要对放置模式调整阶段的内在处理机制做更深入了解.首先，改变一个服务设施的放置位置可能引发2种后果：

1) 请求节点子集V_{Q, j}, j∈V_R-free均保持不变；

2) 上述部分请求节点子集发生改变.

对第1种情况的分析相对简单，此时每个服务设施都是基于贪婪策略在范围有限的搜索域内进行放置位置上的调整.然而，对第2种情况的分析要复杂得多，此时某些服务设施在放置位置上的改变将会增加/减少相邻服务节点所服务的需求.如图 2所示，这一现象是由2种因素所引起的，分别称之为排斥效应和吸引效应.进一步，排斥效应是指对于一个请求节点而言，原本指派给它的服务节点上的服务设施被移动到一个与该请求节点距离较远的位置，使得这个请求节点到某个其他服务节点的距离更近，导致这个距离更近的服务节点被指派给该请求节点.类似地，吸引效应是服务设施放置位置发生改变之后，对于某些请求节点而言，被更新后的服务节点与该请求节点间的距离小于该请求节点与其原始服务节点之间的距离，最终导致更新后的服务节点被指派给该请求节点，从而使部分V_{Q, j}中的元素发生改变.

无论排斥效应还是吸引效应都有可能引发连锁反应，导致服务设施放置模式调整阶段内的迭代过程持续进行.在上述迭代过程中，尽管不能保证所有服务节点的效用都是不变或者递增的，但算法第15行确保每次迭代后的网络总效用都是递增的，同时这一增量不会小于如下门限值：

$ \delta = {\rm{min}}\;\{ \left| {{a_{{i_1}}}} \right.\left. { - {a_{{i_2}}}} \right\|{a_{{i_1}}} \ne {a_{{i_2}}}, \forall {i_1}, {i_2} \in {V_{\rm{Q}}}\} $

上述分析推导出了算法最坏情况下的时间复杂度，进一步考虑p=|V_Q|这一极限情况，用R_max 表示这时的总效用.那么，算法最多经历R_max /δ次服务设施放置位置上的移动.当所有需求均为有限值时，这一结果可以表示为O(N).进一步，每次服务设施放置位置上的移动最多涉及p次候选位置的搜索，每次搜索都将在一个节点数目不超过N的范围内不断尝试.每次尝试最多改变|V_Q|个请求-响应指派关系，而这一过程的时间复杂度将不超过O(Np).综上所述，整个算法的时间复杂度不超过O(N³p²).

4 仿真结果

通过一个代表性的数值仿真来评估算法1(PA, proposed algorithm)的性能.仿真中，搜索半径被设置为2.出于比较目的，仿真同时考虑了另外2种经典算法：穷举算法(EA, exhaustive algorithm)和贪婪算法(GA, greedy algorithm)^[7].穷举算法是指以暴力搜索的方式遍历整个解空间，通过逐次比较确定问题的最优解，而贪婪算法是指仅使用贪婪策略方式来依次确定出每个服务设施的放置位置，即在不改变现有服务节点位置的前提下为新增服务设施寻找能使总效用达到最大的节点位置.出于一般性考虑，仿真中的网络拓扑是节点总数以及请求节点数目(每个请求节点配置单位需求)给定时的随机图，其中任意2个节点相邻的概率被设置为0.3.主要仿真项目包括算法的归一化程序运行时间以及归一化平均性能差距，结果如表 2和表 3所示.出于拓扑上的随机性，表中的每个数据都是100次独立实验的平均结果.

根据表 2可以看出，EA运行时间确实是网络规模N的指数级函数.另外，该运行时间也受参数p的影响，即N和p同时增加时运行时间的变化幅度大于只有N增加时的情况，这一结论对另外2种算法依旧适用.比较显示，PA、EA运行时间随网络规模递增幅度要明显小于EA.尽管PA的运行时间略高于GA，但相对于EA，这一差距是可接受的. 表 3展示了PA和GA相对于由EA所确定的理论最优值之间的归一化的平均性能差距.可以看出，相对于GA-EA间的性能差距，PA-EA之间的差距更小.因此，PA在性能与算法复杂度之间展示了一种新的折中关系，这对比较关注性能的应用来说具有重要意义.

5 结束语

研究了移动边缘计算中的服务设施放置问题，将其建模成一个(p+m)-中点问题，进而提出了一种基于禁忌搜索策略的启发式放置算法.提出的算法有着广泛的适用性，能够用于任意拓扑和需求分布的数据网络.相对于贪婪算法，提出的算法在性能和复杂度之间实现了更好的折中：提出的算法有着更接近于理论最优的性能，但仍是多项式时间的.当所引入的服务设施数目等于请求节点数目时，执行该算法能够得到最优放置模式.为了使提出的算法更具有实用价值，下一步将研究对不同链路上的通信成本予以区分，关注此链路权值在成本计算方面的作用，这将有助于与一些更实用的性能评估指标，如QoS、可用信道带宽以及内容获取时延等建立更为深入地联系.