2. 南京工程学院 智能装备产业技术研究院, 南京 211167;
3. 北京邮电大学 自动化学院, 北京 100876
基于线性方程组及条件极值理论,针对三分支机器人逆运动学问题,提出了一种改进的最小范数逆解算法,避免了传统最小范数逆解中雅可比矩阵广义逆的复杂计算.针对操作分支关节数不小于任务空间维数的情况,进一步利用施密特正交化过程进行简化,提高了运算的实时性.搬运物体的仿真实例结果验证了所提算法的有效性.
2. Industrial Technology Research Institute of Intelligent Equipment, Nanjing Institute of Technology, Nanjing 211167, China;
3. School of Automation, Beijing University of Posts and Telecommunications, Beijing 100876, China
The inverse kinematics for trinal-branch robotic manipulator is researched based on the theory of linear equations set and conditional extremum, and an improved algorithm for least-norm inverse kinematics solution is proposed. The complicated calculation in conventional algorithm for the generalized inverse of Jacobian is avoided in this algorithm, especially, if the joint degree of each handling branch is equal to or more than the dimension of task space, a further simplified calculation can be obtained with the introduction of the Schimidt orthogonalization procedure. The proposed algorithm is of the higher real-time computation capacity than the common method, through the simulation of carrying a single object, the validity of the proposed algorithm is certificated.
为了增加机器人的工作空间和灵活性,空间机器人已向着多臂、多分支的方向发展.其中,三分支机器人由于其结构紧凑、操控灵活且具备协调操作能力,因此成为多分支机器人研究的热点[1].逆运动学求解是三分支机器人协调操作研究的基础.近年来,学者们在三分支机器人建模、逆运动学分析、步态规划等方面做了相关研究[2-5].可以发现,由于三分支机器人任务空间维数和关节数目的增加,造成其雅可比矩阵广义逆运算量的极大增加和算法实时性的下降.
笔者在前人研究基础上,提出了一种三分支机器人最小范数逆解算法.该算法运用线性方程组理论,构造了特解加齐次解形式的逆解结构和统一解算模型,且无需直接求解雅可比矩阵广义逆,从而有效地提高了三分支机器人逆解的实时性.结合搬运物体操作的仿真实例,验证了算法的有效性.
1 最小范数逆解的结构三分支机器人的最小范数逆解是由单臂冗余度机器人推广而来,这里首先以n自由度单臂冗余度机器人说明最小范数逆解的结构.设任务空间维数为m(m≤6),满足m < n,可得机器人关节速度为
| $ \mathit{\boldsymbol{\dot q}} = {\mathit{\boldsymbol{J}}^ + }{{\mathit{\boldsymbol{\dot x}}}_e} + \left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{J}}^ + }\mathit{\boldsymbol{J}}} \right)\mathit{\boldsymbol{\dot \phi }} $ | (1) |
其中:
下面利用雅可比矩阵的性质构造最小范数解的结构形式.当J满秩且非奇异时,可从J中提取m个线性无关的列向量构成m×m阶矩阵J1,剩余的r(r=n-m)个列向量构成m×r阶矩阵J0,则有
| $ \mathit{\boldsymbol{J}} = \left[ {\mathit{\boldsymbol{J}}_0^{m \times r}\quad \mathit{\boldsymbol{J}}_1^{m \times m}} \right] $ | (2) |
| $ \mathit{\boldsymbol{\dot q}} = {{\mathit{\boldsymbol{\dot q}}}_p} + {{\mathit{\boldsymbol{\dot q}}}_h} $ | (3) |
其中
| $ {{\mathit{\boldsymbol{\dot q}}}_h} = \left[ {\begin{array}{*{20}{l}} {{{\dot q}_{h1}}}&{{{\dot q}_{h2}}}& \cdots &{{{\dot q}_{hr}}} \end{array}} \right]{\mathit{\boldsymbol{\kappa }}^{r \times 1}} $ | (4) |
其中:κ∈Rr×1为由任意实数组成的系数矢量,即
| $ \mathit{\boldsymbol{\kappa }} = {\left( {\begin{array}{*{20}{l}} {{\kappa _1}}&{{\kappa _2}}& \cdots &{{\kappa _r}} \end{array}} \right)^{\rm{T}}} $ | (5) |
特解
| $ {{\mathit{\boldsymbol{\dot q}}}_p} = \left[ {\begin{array}{*{20}{c}} {{{\bf{0}}^{r \times 1}}}\\ {{{\left( {\mathit{\boldsymbol{J}}_1^{m \times m}} \right)}^{ - 1}}\mathit{\boldsymbol{\dot x}}_e^{m \times 1}} \end{array}} \right],{{\mathit{\boldsymbol{\dot q}}}_h} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}^{r \times r}}}\\ { - {{\left( {\mathit{\boldsymbol{J}}_1^{m \times m}} \right)}^{ - 1}}\mathit{\boldsymbol{J}}_0^{m \times r}} \end{array}} \right]{\mathit{\boldsymbol{\kappa }}^{r \times 1}} $ | (6) |
将式(6)的结果代入式(3)得
| $ \mathit{\boldsymbol{\dot q}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{\kappa }}\\ {\mathit{\boldsymbol{J}}_1^{ - 1}\left( {{{\mathit{\boldsymbol{\dot x}}}_e} - {\mathit{\boldsymbol{J}}_0}\mathit{\boldsymbol{\kappa }}} \right)} \end{array}} \right] $ | (7) |
式(7)为利用雅可比矩阵性质构造的逆解
| $ \mathit{\boldsymbol{\dot q}} = {{\mathit{\boldsymbol{\dot q}}}_p} + {\kappa _1}{{\dot q}_{h1}} + {\kappa _2}{{\dot q}_{h2}} + \cdots + {\kappa _r}{{\dot q}_{hr}} $ | (8) |
则根据式(8)可得
| $ \begin{array}{*{20}{c}} {{{\left\| {\mathit{\boldsymbol{\dot q}}} \right\|}^2} = {{\left\| {{{\mathit{\boldsymbol{\dot q}}}_p} + \sum\limits_{i = 1}^r {{\kappa _i}} {{\dot q}_{hi}}} \right\|}^2} = }\\ {{{\left( {{{\mathit{\boldsymbol{\dot q}}}_p} + \sum\limits_{i = 1}^r {{\kappa _i}} {{\dot q}_{hi}}} \right)}^{\rm{T}}}\left( {{{\mathit{\boldsymbol{\dot q}}}_p} + \sum\limits_{i = 1}^r {{\kappa _i}} {{\dot q}_{hi}}} \right)} \end{array} $ | (9) |
要得到最小范数逆解
| $ \frac{{\partial {{\left\| {\mathit{\boldsymbol{\dot q}}} \right\|}^2}}}{{\partial {\kappa _i}}} = 2{\left( {{{\mathit{\boldsymbol{\dot q}}}_p} + \sum\limits_{j = 1}^r {{\kappa _j}} {{\dot q}_{hj}}} \right)^{\rm{T}}}{{\dot q}_{hi}} = 0 $ | (10) |
式(10)关于κi(i=1~r)的r×r阶线性方程组,κi(i=1~r)可由式(10)求出,将结果代入式(7)即可求得最小范数逆解.
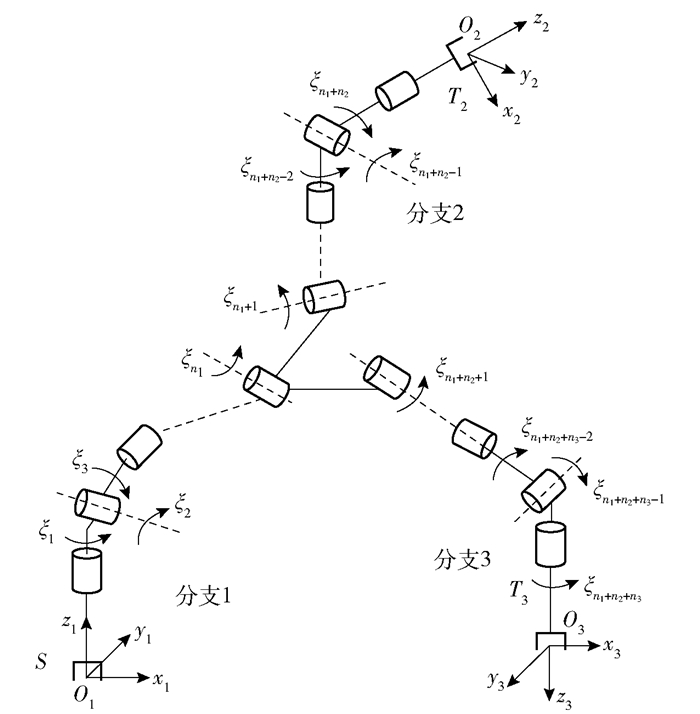
2 三分支机器人最小范数逆解 2.1 三分支机器人模型一般性三分支机器人模型如图 1所示.
|
图 1 三分支机器人模型 |
设机器人的三分支分别是分支1、分支2和分支3,坐标系S为基坐标系,坐标系T2和T3分别为与机器人分支2和3末端固连的工具坐标系.支上的关节数目分别为n1、n2和n3,总关节数目为n=n1+n2+n3.作业时,为满足灵活性要求,在设计上一般具有冗余关节,要求自由度数n大于任务空间的最大维数12,即总关节数目满足n>12.
2.2 三分支机器人最小范数逆解模型采用如图 1所示的三分支机器人模型,分支1和2、3分别组成两个单链的串联机械臂,记为M2与M3.为简化分析过程,做以下符合实际情况的假设.设分支2和3关节数目相同,即n2=n3,则M2与M3两个单链臂的自由度数相同,记为n′=n1+n2,设各自的末端任务空间维数都为m,且分别对应的雅可比矩阵JM2和JM3为满秩非奇异矩阵,即满足Rank(JM2)=Rank(JM3)=m.
在以上条件假设下,单链臂M2和M3各自对应的逆解
| $ {{\mathit{\boldsymbol{\dot q}}}_{M2}} = {\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{\kappa }}_2}}&{{\mathit{\boldsymbol{\eta }}_2}} \end{array}} \right]^{\rm{T}}},{{\mathit{\boldsymbol{\dot q}}}_{M3}} = {\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{\kappa }}_3}}&{{\mathit{\boldsymbol{\eta }}_3}} \end{array}} \right]^{\rm{T}}} $ | (11) |
其中:
由于三分支机器人存在耦合分支(分支1),故需满足
1) 当n1 < r的情况
可令κ2和κ3的前n1个元素对应相等,则有
| $ \mathit{\boldsymbol{\dot q}} = {\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{\kappa }}_2}}&{{\mathit{\boldsymbol{\eta }}_2}}&{\mathit{\boldsymbol{\eta }}_3^\prime } \end{array}} \right]^{\rm{T}}} $ | (12) |
其中:η′3=(κ3, n1+1, …, κ3, r, η3, 1, …, η3, m)T∈Rn′-n1.显然组合后的基础解系数矢量κ′为
| $ {\mathit{\boldsymbol{\kappa }}^\prime } = {\left( {{\kappa _{2,1}}, \cdots ,{\kappa _{2,r}},{\kappa _{3,{n_1} + 1}}, \cdots ,{\kappa _{3,r}}} \right)^{\rm{T}}} $ | (13) |
此时
| $ \frac{{\partial {{\left\| {\mathit{\boldsymbol{\dot q}}} \right\|}^2}}}{{\partial {{\kappa '}_i}}} = \frac{{\partial \left( {{{\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{\kappa }}_2}}&{{\mathit{\boldsymbol{\eta }}_2}}&{\mathit{\boldsymbol{\eta }}_3^\prime } \end{array}} \right]}^{\rm{T}}}\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{\kappa }}_2}}&{{\mathit{\boldsymbol{\eta }}_2}}&{\mathit{\boldsymbol{\eta }}_3^\prime } \end{array}} \right]} \right)}}{{\partial {{\kappa '}_i}}} = 0 $ | (14) |
显然由式(14)可以得到关于κ′i的2r-n1个线性方程构成的方程组,可表示为如下矩阵形式:
| $ {\mathit{\boldsymbol{J}}_k}\mathit{\boldsymbol{\kappa '}} = \mathit{\boldsymbol{\tau }} $ | (15) |
其中:Jk∈R(2r-n1)×(2r-n1),τ∈R(2r-n1)为κ′的方程组系数矩阵和常数向量.因Jk为方阵,在非奇异情况下得
| $ \mathit{\boldsymbol{\kappa '}} = \mathit{\boldsymbol{J}}_k^{ - 1}\mathit{\boldsymbol{\tau }} $ | (16) |
将κ′的结果代入式(12)可得到最小范数逆解.
2) 当n1=r的情况
可令κ2和κ3的全部元素对应相等,则有
| $ \mathit{\boldsymbol{\dot q}} = {\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{\kappa }}_2}}&{{\mathit{\boldsymbol{\eta }}_2}}&{{\mathit{\boldsymbol{\eta }}_3}} \end{array}} \right]^{\rm{T}}} $ | (17) |
显然此时组合后的基础解系数矢量κ′为
| $ {\mathit{\boldsymbol{\kappa }}^\prime } = {\mathit{\boldsymbol{\kappa }}_2} = {\left( {{\kappa _{2,1}}, \cdots ,{\kappa _{2,r}}} \right)^{\rm{T}}} $ | (18) |
以下解算过程同情况(1),不再赘述.情况(2)可认为是情况(1)在η′3=η3时的特例.
3) 当n1>r的情况
令κ2和κ3的全部元素对应相等,同时令η2和η3的前n1-r项元素对应相等,则有
| $ \mathit{\boldsymbol{\dot q}} = {\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{\kappa }}_2}}&{{\mathit{\boldsymbol{\eta }}_2}}&{\mathit{\boldsymbol{\eta }}_3^{\prime \prime }} \end{array}} \right]^{\rm{T}}} $ | (19) |
其中:η″3=(η3, n1-r+1, …, η3, m)T∈Rn′-n1,由于κ2=κ3,而η2和η3的元素分别是κ2和κ3的线性组合,故组合后的基础解系数矢量κ′仍可表示为式(18)的形式.
对
| $ \left. \begin{array}{l} \min {\left\| {\mathit{\boldsymbol{\dot q}}\left( {{\mathit{\boldsymbol{\kappa }}^\prime }} \right)} \right\|^2},{\mathit{\boldsymbol{\kappa }}^\prime } = {\left( {{\kappa _{2,1}}, \cdots ,{\kappa _{2,r}}} \right)^{\rm{T}}}\\ {\rm{s}}.{\rm{t}}\;{\mathit{\boldsymbol{\eta }}_{2,i}}\left( {{\mathit{\boldsymbol{\kappa }}^\prime }} \right) = {\mathit{\boldsymbol{\eta }}_{3,i}}\left( {{\mathit{\boldsymbol{\kappa }}^\prime }} \right),\mathit{i}{\rm{ = 1\sim}}{{\rm{n}}_{\rm{1}}}{\rm{ - r}} \end{array} \right\} $ | (20) |
利用拉格朗日乘子法求解,引入n1-r个常数λi,记λ=(λ1, λ1, …, λn1-r)T,则式(20)等价于无条件极值问题:
| $ \begin{array}{*{20}{c}} {f\left( {{\mathit{\boldsymbol{\kappa }}^\prime },\mathit{\boldsymbol{\lambda }}} \right) = {{\left\| {\mathit{\boldsymbol{\dot q}}\left( {{\mathit{\boldsymbol{\kappa }}^\prime }} \right)} \right\|}^2} + \sum\limits_{i = 1}^{{n_1} - r} {{\lambda _i}} \left( {{\mathit{\boldsymbol{\eta }}_{2,i}}\left( {{\mathit{\boldsymbol{\kappa }}^\prime }} \right) - } \right.}\\ {\left. {{\mathit{\boldsymbol{\eta }}_{3,i}}\left( {{\mathit{\boldsymbol{\kappa }}^\prime }} \right)} \right)} \end{array} $ | (21) |
f(κ′, λ)对κ′和λ中每个元素求偏导并等于0得
| $ \left. \begin{array}{l} \frac{{\partial f\left( {{\mathit{\boldsymbol{\kappa }}^\prime },\mathit{\boldsymbol{\lambda }}} \right)}}{{\partial \kappa _i^\prime }} = 0,\;\;\;\;i = 1 \sim r\\ \frac{{\partial f\left( {{\mathit{\boldsymbol{\kappa }}^\prime },\mathit{\boldsymbol{\lambda }}} \right)}}{{\partial {\lambda _j}}} = 0,\;\;\;\;j = 1 \sim {n_1} - r \end{array} \right\} $ | (22) |
由式(22)可求出κ′i(i=1~r),再代入式(19)得出
在2.2节所述的3种情况中,前两种情况下由于r=n1+n2-m(或r=n1+n3-m),故n2≥m且n3≥m(仍假设n2=n3),即两个操作分支的关节数不小于任务空间维数,在这种条件下,计算模型可做进一步简化,得到更简洁的形式.
根据式(11)、式(16)和式(22),可以构造三分支机器人整体的特解
1) 当n1 < r时
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot q}}}_p} = {{\left[ {\begin{array}{*{20}{c}} {{{\bf{0}}^{r \times 1}}}&{{{\left( {{\mathit{\boldsymbol{J}}_{M2,1}}} \right)}^{ - 1}}{{\mathit{\boldsymbol{\dot x}}}_{2,e}}}&{{{\bf{0}}^{\left( {{n_3} - n} \right) \times 1}}}&{{{\left( {{{\bf{J}}_{M3,1}}} \right)}^{ - 1}}{{\mathit{\boldsymbol{\dot x}}}_{3,e}}} \end{array}} \right]}^{\rm{T}}}}\\ {{{\mathit{\boldsymbol{\dot q}}}_h} = }\\ {{{\left[ {{\mathit{\boldsymbol{I}}^{r \times r}} - {{\left( {{\mathit{\boldsymbol{J}}_{M2,1}}} \right)}^{ - 1}}{\mathit{\boldsymbol{J}}_{M2,0}}{\mathit{\boldsymbol{I}}^{\left( {{n_3} - r} \right) \times \left( {{n_3} - r} \right)}}\quad {{\left( {{\mathit{\boldsymbol{J}}_{M3,1}}} \right)}^{ - 1}}{\mathit{\boldsymbol{J}}_{M3,0}}} \right]}^{\rm{T}}}{\mathit{\boldsymbol{\kappa }}^\prime }} \end{array} $ | (23) |
2) 当n1=r时
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot q}}}_p} = {{\left[ {\begin{array}{*{20}{c}} {{{\bf{0}}^{r \times 1}}}&{{{\left( {{\mathit{\boldsymbol{J}}_{M2,1}}} \right)}^{ - 1}}{{\mathit{\boldsymbol{\dot x}}}_{2,e}}}&{{{\left( {{\mathit{\boldsymbol{J}}_{M3,1}}} \right)}^{ - 1}}{{\mathit{\boldsymbol{\dot x}}}_{3,e}}} \end{array}} \right]}^{\rm{T}}}}\\ {{{\mathit{\boldsymbol{\dot q}}}_h} = {{\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}^{r \times r}}}&{ - {{\left( {{\mathit{\boldsymbol{J}}_{M2,1}}} \right)}^{ - 1}}{\mathit{\boldsymbol{J}}_{M2,0}}}&{{{\left( {{\mathit{\boldsymbol{J}}_{M3,1}}} \right)}^{ - 1}}{\mathit{\boldsymbol{J}}_{M3,0}}} \end{array}} \right]}^{\rm{T}}}{\mathit{\boldsymbol{\kappa }}^\prime }} \end{array} $ | (24) |
式(23)和式(24)中,κ′可统一记为
| $ {\mathit{\boldsymbol{\kappa }}^\prime } = {\left( {\begin{array}{*{20}{l}} {{\kappa }_1^\prime }&{{\kappa }_2^\prime }& \cdots &{{\kappa }_\alpha ^\prime } \end{array}} \right)^{\rm{T}}} $ | (25) |
则逆解
| $ \mathit{\boldsymbol{\dot q}} = {{\mathit{\boldsymbol{\dot q}}}_p} + \mathit{\kappa }_1^\prime {{\dot q}_{h1}} + \mathit{\kappa }_1^\prime {{\dot q}_{h2}} + \cdots + \mathit{\kappa }_\alpha ^\prime {{\dot q}_{h\alpha }} $ | (26) |
其中:(
设(
| $ \mathit{\boldsymbol{\dot q}} = {{\mathit{\boldsymbol{\dot q}}}_p} + \kappa _1^{\prime \prime }\dot q_{h1}^\prime + \kappa _2^{\prime \prime }\dot q_{h2}^\prime + \cdots + \kappa _\alpha ^{\prime \prime }\dot q_{h\alpha }^\prime $ | (27) |
其中:κ″=(κ″1κ″2…κ″α)T为正交化后新的系数向量.对每个κ″i(i=1~α)求偏导并令其等于0得
| $ \frac{{\partial {{\left\| {\mathit{\boldsymbol{\dot q}}} \right\|}^2}}}{{\partial \kappa _i^{\prime \prime }}} = 2{\left( {{{\mathit{\boldsymbol{\dot q}}}_p} + \sum\limits_{j = 1}^\alpha {\kappa _j^{\prime \prime }\mathit{\boldsymbol{\dot q}}_{hj}^\prime } } \right)^{\rm{T}}}\mathit{\boldsymbol{\dot q}}_{hi}^\prime = 0 $ | (28) |
则通过式(28)可求出κ″i,得
| $ \kappa _i^{\prime \prime } = - \frac{{\mathit{\boldsymbol{\dot q}}_p^{\rm{T}}\mathit{\boldsymbol{\dot q}}_{hi}^\prime }}{{\mathit{\boldsymbol{\dot q}}_{hi}^{\prime {\rm{T}}}\mathit{\boldsymbol{\dot q}}_{hi}^\prime }} $ | (29) |
将式(29)代入式(26)得
| $ {{\mathit{\boldsymbol{\dot q}}}_{\min }} = {{\mathit{\boldsymbol{\dot q}}}_p} - \sum\limits_{i = 1}^\alpha {\left( {\frac{{\mathit{\boldsymbol{\dot q}}_p^{\rm{T}}\mathit{\boldsymbol{\dot q}}_{hi}^\prime }}{{\mathit{\boldsymbol{\dot q}}_{hi}^{\prime {\rm{T}}}\mathit{\boldsymbol{\dot q}}_{hi}^\prime }}} \right)\mathit{\boldsymbol{\dot q}}_{hi}^\prime } $ | (30) |
式(30)即为简化的最小范数逆解形式.
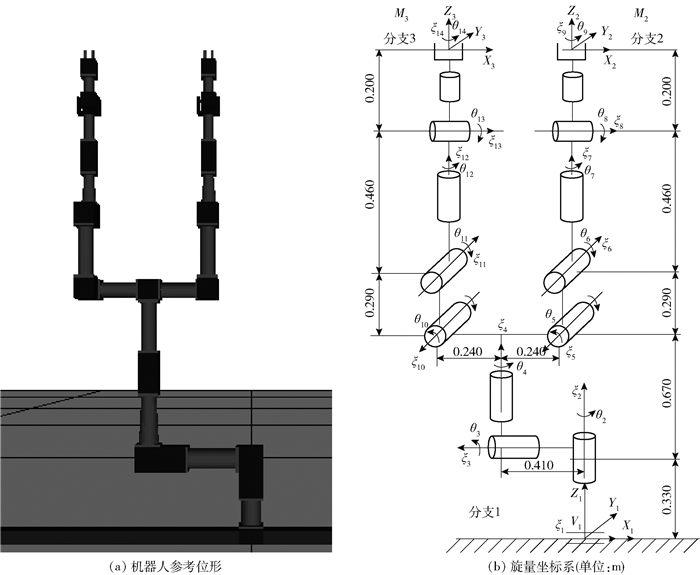
3 算例仿真与分析以如图 2(a)所示的三分支机器人为例,对本文提出的最小范数逆解算法进行搬物体操作的实例仿真.其中,分支1为支撑分支,具有3个旋转关节,其基部有一个移动导轨. 2个操作分支2和3各有5个旋转关节.整个机器人系统共有14个自由度.
|
图 2 三分支机器人参考位形及旋量法建模 |
采用旋量法进行建模,以如图 2(a)所示位形为参考位形建立如图 2(b)所示的旋量坐标系.
在参考位形下,各关节旋量坐标(单位:m)为
| $ {\xi _1} = \left\{ {1,0,0,0,0,0} \right\}\;\;\;{\xi _2} = \left\{ {0,0,0,0,0,1} \right\} $ |
| $ {\xi _3} = \left\{ {0, - 0.33,0, - 1,0,0} \right\} $ |
| $ {\xi _4} = \{ 0,0.41,0,0,0,1\} $ |
| $ {\xi _5} = \{ 1,0,0.17,0, - 1,0\} $ |
| $ {\xi _6} = \{ - 1.29,0, - 0.17,0,1,0\} $ |
| $ {\xi _7} = \{ 0,0.17,0,0,0,1\} $ |
| $ {\xi _8} = \{ 0,1.75,0,1,0,0\} $ |
| $ {\xi _9} = \{ 0,0.17,0,0,0,1\} $ |
| $ {\xi _{10}} = \{ 1,0,0.65,0, - 1,0\} $ |
| $ {\xi _{11}} = \{ - 1.29,0, - 0.65,0,1,0\} $ |
| $ {\xi _{12}} = \{ 0,0.65,0,0,0,1\} $ |
| $ {\xi _{13}} = \{ 0,1.75,0,1,0,0\} $ |
| $ {\xi _{14}} = \{ 0,0.65,0,0,0,1\} $ |
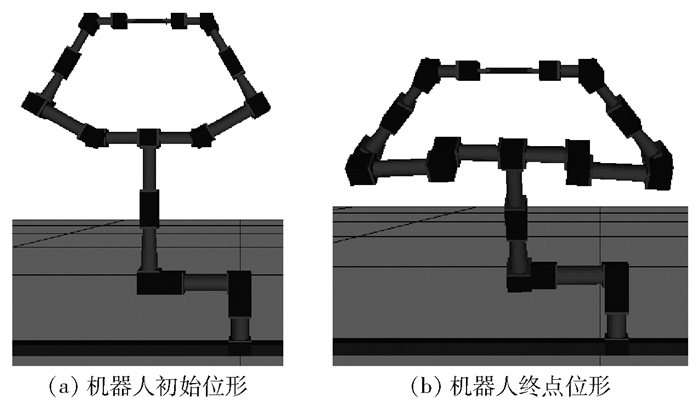
设M2和M3末端刚性夹持物体, 三分支机器人的初始关节值为q0=(0, 0, 0, 0, -60, -90, 90, -60, 0, 60, 90, 90, 60, 0),其中移动关节单位为m,转动关节单位为度.根据以上设置,三分支机器人的初始位形如图 3(a)所示.下文中涉及物体位置坐标及位置误差的单位均为m.物体中心位于M2和M3末端的连线中点处,其初始位置坐标为(-0.41, 0, 1.543 4),物体姿态搬运物体时不变,设为与M2末端相同.物体中心移动到(-0.3, -0.7, 1.1),则M2和M3的终点期望位置坐标分别为
|
图 3 搬运物体协调操作 |
| $ g_{st,2}^d = \left( { - 0.238\;9, - 0.7,1.1} \right) $ |
| $ g_{st,3}^d = \left( { - 0.361\;1, - 0.7,1.1} \right) $ |
采用带抛物线过渡域的线性插值法规划物体的运动.设过渡域加速度acc=0.04 m/s2,运动时间T=10 s,设单位插补时间t0=0.05 s,插补次数k=200.分别采用广义逆算法和本文算法进行求解,可得终点处的逆解结果如表 1所示.
|
|
表 1 广义逆算法和本文算法计算结果比较 |
在上述实例基础上进行实时性比较.算法运行环境为mathematica5.2,分别测试运动仿真时间T取5、10、15、20和25 s,即插补次数k分别为100、200、300、400和500的结果,如表 2所示.
|
|
表 2 广义逆算法和本文算法计算实时性比较 |
由表 1可见,2种最小范数逆解结果只有微小误差,这验证了2.2节最小范数逆解算法的正确性,同时由表 2可见后者的算法平均耗时只有前者的0.73左右,可见后者提高了算法实时性.
计算得M2和M3的终点实际位置坐标为
| $ g_{st,2}^c = \left( { - 0.239\;2, - 0.698\;6,1.098\;5} \right) $ |
| $ g_{st,3}^c = \left( { - 0.360\;7, - 0.698\;6,1.098\;5} \right) $ |
实际和期望位置误差仅为(-0.000 3, -0.001 4, -0.001 5)和(0.000 4, -0.001 4, -0.001 5),结果验证了本文算法的正确性,机器人终点位形如图 3(b)所示.
将终点关节值代入正解可计算出物体实际终点位置为(-0.300 1,-0.699 6,1.099 5), 计算精度达到了1×10-3,满足试验精度的要求.
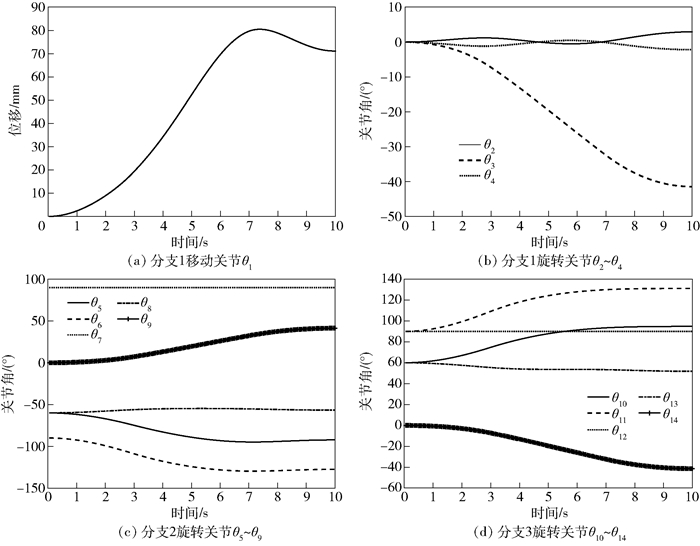
为进一步验证算法的有效性,在Adams/View中创建机器人模型并进行运动仿真,仿真数据导入Matlab后得到在搬物体过程中的关节变化曲线和目标物体运动位移变化曲线分别如图 4和图 5所示.
|
图 4 关节运动变化曲线 |
|
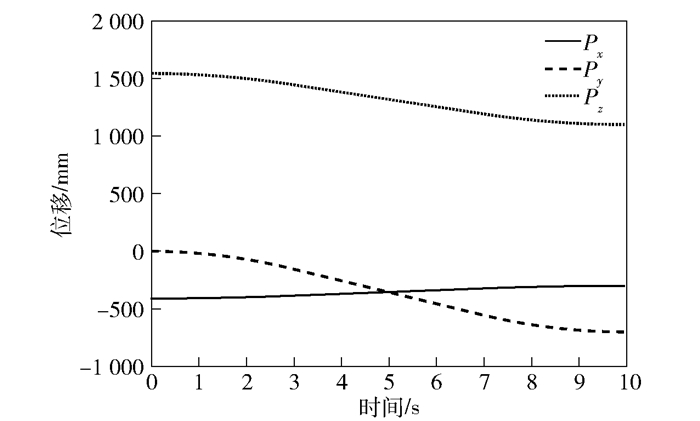
图 5 目标物体中心运动位移曲线 |
由图 4可见,三分支机器人关节在搬物体运动过程中轨迹平滑,没有超出关节极限或出现奇异现象.由图 5可见,目标物体中心运动位移结果亦符合仿真测试实例的运动要求,证明了本文算法的有效性.
4 结束语运用线性方程组和条件极值理论,提出了一种具有较高实时性的最小范数逆解算法,并建立了统一的逆运动学求解模型.当操作分支关节数不小于任务空间维数时,可进一步得出更简化的算法形式.通过搬物体协调操作仿真实例,验证了算法的有效性,该算法对速度级控制法的最小范数逆解解算做了有效改进,可应用于三分支机器人的实际操作.
| [1] |
刘宏, 蒋再男, 刘业超. 空间机械臂技术发展综述[J]. 载人航天, 2015, 21(5): 435-443. Liu Hong, Jiang Zainan, Liu Yechao. Review of space manipulator technology[J]. Manned Space flight, 2015, 21(5): 435-443. DOI:10.3969/j.issn.1674-5825.2015.05.002 |
| [2] |
孙汉旭, 贾庆轩, 张秋豪, 等. 基于三分支机器人关节空间轨迹规划的研究[J]. 北京邮电大学学报, 2006, 29(3): 81-85. Sun Hanxu, Jia Qingxuan, Zhang Qiuhao, et al. Trajectory planning in joint space based on tri-branch robot[J]. Journal of Beijing University of Posts and Telecommunications, 2006, 29(3): 81-85. DOI:10.3969/j.issn.1007-5321.2006.03.019 |
| [3] |
叶平, 孙汉旭. 具有冗余度的三分支空间机器人逆运动学分析[J]. 机械工程学报, 2005, 41(11): 58-62. Ye Ping, Sun Hanxu. Analysis of inverse kinematics for three-branch space robot with redundancy[J]. Chinese Journal of Mechanical Engineering, 2005, 41(11): 58-62. DOI:10.3321/j.issn:0577-6686.2005.11.010 |
| [4] |
张宇.自重构多分支空间机器人动力学与轨迹规划的研究[D].哈尔滨: 哈尔滨工业大学, 2014.
|
| [5] |
赵京东, 韩均广, 倪风雷, 等. 面向空间站桁架的三分支机器人的步态规划与研究[J]. 载人航天, 2018, 24(1): 14-19. Zhao Jingdong, Han Junguang, Ni Fenglei, et al. Gait planning and study of climbing robot with three branches for space station truss[J]. Manned Spaceflight, 2018, 24(1): 14-19. DOI:10.3969/j.issn.1674-5825.2018.01.003 |


