2. 重庆生物感知与智能信息处理重点实验室, 重庆 400044
针对频谱资源中授权频段因信道质量和信号干扰等因素导致的感知频谱利用率不高的问题,提出了基于大规模天线空间信道控制的频谱感知资源分配方式.通过波束成型技术使主瓣波束对准期望用户,而在干扰源方向放置零陷,可有效地抑制对次级用户的干扰,并确保次级用户对感知频谱的使用,从而进一步提高系统的频谱效率.仿真结果显示,在信噪比为5 dB和10 dB时,所提方案的谱效率(系统吞吐量)优于其他策略.
2. Chongqing Key Laboratory of Bio-Perception and Intelligent Information Processing, Chongqing 400044, China
Aiming at problem of lower utilization the authorized spectrum, due to channel quality and transmission power interference, a resource allocation technology was proposed based on the large scale antenna spatial channel controlling. Main lobes beam of multiple antenna beam forming points to the desired user and places the nulls in the interference direction, which can effectively suppress interference to secondary users and ensure that aware spectrum is used. As a result, the utilization ratio of frequency spectrum increased further in the whole system. The simulation results showed the throughput of the proposed method is better than the scheme in the literatures when signal to noise ratio is 5 dB and 10 dB.
新一代通信系统除了网络的极度复杂、负载流量的海量增加外,无线频谱资源也将面临一个巨大的瓶颈.虽然对超高频谱的扩展应用有利于缓解频谱的不足问题,但超高频谱的快速衰减特性也限制了其广泛的使用.因此如何更好的利用这些稀缺的资源成为一个技术性问题日益受人们的到重视. J. Mitola博士指出:由于固定的频谱资源管理分配制度,使已授权的频谱中依然有很多空闲频段(称为频谱漏洞)没有被很好的利用,这降低了稀缺频谱资源的利用率.然而认知无线电就是一项能够利用授权频谱中的空闲频段的技术.该技术通过频谱感知系统识别授权频谱中的空闲频段经整合后分配给有机会使用那些没有被授权用户使用授权频段的次级用户,从而使授权频谱的利用率进一步提高.之后, 认知网络的优点和面对的一些技术挑战[1]已经被广泛而深入的探讨和研究.在认知网络中,当次级用户使用主用户频段或者相邻频段将会产生互信道和跨信道的干扰以至于影响了在授权频段主用户的服务,所以基于正交频分多址复接技术和传输功率约束的资源分配方式[2-4]降低了此方面的干扰.另外,多蜂窝感知联合功率约束资源分配和优化算法[5-6]不仅提高了感知频谱的利用效率而且也很好的解决了室内感知覆盖.
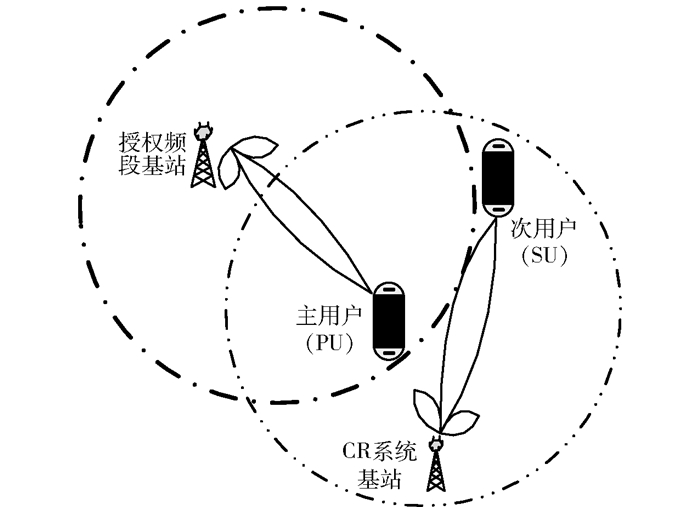
笔者在参考文献[2-3, 5-6]中发现,这些方案不论是基于提高能源传输效率感知系统还是采用功率约束的优化算法的感知系统,次级用户对授权频段主要用户的干扰或者对相邻频段的干扰都没有降低或减少.鉴于此,研究提出基于大规模天线的波束成型的空间信道控制的频谱感知资源分配技术.如图 1中,授权频段基站附近部署一个感知系统基站.授权的主要用户和非授权的次级用户分别处于其覆盖范围内.若利用大规模天线的信道控制技术[7-9, 11],在通过调整对期望用户的波束方向使主瓣波束对准期望用户而在产生干扰方向放置零陷,从而减少授权用户和非授权用户的之间的干扰.这样既保证了主要用户的服务质量,又允许次级用户对授权频段的使用,从而提高频谱的利用效率.通过对文献[6]的方式比较,结果显示本文方式的频谱效率明显提高.因此,基于大规模MIMO信道方向控制的频谱感知系统能有效提高频谱利用效率.
|
图 1 基于空间信道控制的感知系统 |
为便于描述,假定在同一区域部署一个授权主基站和一个感知系统基站,采用非合作方式传输数据.主基站和认知系统均采用多天线收发方式,天线数量Nt根,带宽用F={f1, …, fN}表示N个子载波.限定感知系统采用填充共享方式共享频谱.主用户和次级用户数有K个,且N>K,用户的接收天线Nr根.整个小区的上下行传输采用正交频分多址接入方式,且‖sk‖2=1.对于感知用户k占用第n个感知谱时的接收信号可以表示为
| $ \begin{array}{*{20}{c}} {Y_{n,k}^m = a_{n,k}^m\sqrt {{P_k}} \mathit{\boldsymbol{H}}_k^m\mathit{\boldsymbol{W}}_k^m{\mathit{\boldsymbol{s}}_k} + }\\ {\sum\limits_{m = 1}^{{M_B}} {\sum\limits_{\begin{array}{*{20}{c}} {j = 1}\\ {j \ne k} \end{array}}^K {\sum\limits_{\begin{array}{*{20}{c}} {i = 1}\\ {i \ne n} \end{array}}^N {a_{i,j}^m\sqrt {{P_j}} \mathit{\boldsymbol{H}}_{j,k}^m\mathit{\boldsymbol{W}}_{i,j}^m{s_j}} } } + {n_k}} \end{array} $ | (1) |
其中:Pk为用户k分配的功率,Wm, k=[w1, k, …, wNt, k]∈C1×Nt表示CR系统中第m基站的k用户的波束赋形矢量,Hk表示用户k的信道响应矩阵. an, k表示感知频谱占用指示标志当用户k使用第n个感知频谱资源块时用an, k=1,表示;反之an, k=0.为提高感知频谱利用效率采用全小区复用方式,但一个小区中的同一载波只能被一个用户使用.式(1)右边第1项则为用户k接收到的有用信号,第2项为整个系统中同频用户对用户k的干扰信号,第3项为加性高斯噪声.感知系统用户k的接收端信噪比可以表示为
| $ {\gamma _{n,k}} = \frac{{{\mathit{\boldsymbol{P}}_k}{{\left\| {{\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{W}}_k}} \right\|}^2}}}{{1 + \sum\limits_{m = 1}^{{M_B}} {\sum\limits_{\begin{array}{*{20}{c}} {j = 1}\\ {j \ne k} \end{array}}^K {{\mathit{\boldsymbol{P}}_j}{{\left\| {{\mathit{\boldsymbol{H}}_{j,k}}{\mathit{\boldsymbol{W}}_{m,j}}} \right\|}^2}} } }} $ | (2) |
系统要满足最低信噪比要求,即
| $ \frac{{{\mathit{\boldsymbol{P}}_k}{{\left\| {{\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{W}}_k}} \right\|}^2}}}{{1 + \sum\limits_{m = 1}^{{M_B}} {\sum\limits_{\begin{array}{*{20}{c}} {j = 1}\\ {j \ne k} \end{array}}^K {{\mathit{\boldsymbol{P}}_j}{{\left\| {{\mathit{\boldsymbol{H}}_{j,k}}{\mathit{\boldsymbol{W}}_{m,j}}} \right\|}^2}} } }} \ge {\gamma _0} $ | (3) |
由此可得用户k的最低功率为
| $ {p_k} = {\gamma _0}\frac{{1 + \sum\limits_{m = 1}^{{M_B}} {\sum\limits_{\begin{array}{*{20}{c}} {j = 1}\\ {j \ne k} \end{array}}^K {{\mathit{\boldsymbol{P}}_j}{{\left\| {{\mathit{\boldsymbol{H}}_{j,k}}{\mathit{\boldsymbol{W}}_{m,j}}} \right\|}^2}} } }}{{{{\left\| {{\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{W}}_k}} \right\|}^2}}} $ | (4) |
最终感知系统资源分配问题转化为在系统波束信道控制下的系统速率最大化的问题:
| $ \begin{array}{*{20}{c}} {\arg \mathop {\max }\limits_w \sum\limits_{n = 1}^N {\sum\limits_{m = 1}^{{M_B}} {\sum\limits_{k \in {U_m}\left( n \right)} {\log \left( {1 + {\gamma _{{\rm{SINR}}}}(k)} \right)} } } }\\ {{\rm{s}}.\;{\rm{t}}.\;\;\;\sum\limits_{n = 1}^N {\sum\limits_{k \in {U_m}(n)} {{{\left\| {{\mathit{\boldsymbol{w}}_{m,k}}(n)} \right\|}^2}} } \le {P_{m,\max }},m = 1,2, \cdots ,{M_B}} \end{array} $ | (5) |
根据KTT条件,式(5)可以利用拉格朗日对偶法求解:
| $ \begin{array}{*{20}{c}} {\mathit{\Lambda }\left( {W,\lambda } \right) = \sum\limits_{n = 1}^N {\sum\limits_{m = 1}^{{M_B}} {\sum\limits_{k \in {U_m}(n)} {\frac{1}{{\ln 2}}\log \left( {I + {\gamma _{{\rm{SINR}}}}(k)} \right)} } } + }\\ {\sum\limits_{m = 1}^{{M_B}} {{\mathit{\boldsymbol{\lambda }}_m}\left[ {{\mathit{\boldsymbol{P}}_{m,\max }} - \sum\limits_{n = 1}^N {\sum\limits_{k \in {U_m}(n)} {{{\left\| {{\mathit{\boldsymbol{w}}_{m,k}}(n)} \right\|}^2}} } } \right]} } \end{array} $ | (6) |
λ=(λ1, λ2, …, λM)是非负的拉格朗日乘子矢量,定义时隙n用户k∈Um(n)的总信道干扰为
| $ {i_{m,n}}\left( k \right) = \sum\limits_{i = 1}^{{M_B}} {\sum\limits_{\begin{array}{*{20}{c}} {u \in Uj\left( n \right)}\\ {(i,u) \ne (m,k)} \end{array}} {\mathit{\boldsymbol{w}}_{i,u}^{\rm{H}}(n)\mathit{\boldsymbol{h}}_{i,k}^{\rm{H}}(n){\mathit{\boldsymbol{h}}_{i,k}}(n){\mathit{\boldsymbol{w}}_{i,u}}(n)} } $ | (7) |
定义泄漏矩阵:
| $ {\mathit{\boldsymbol{L}}_{m,n}}\left( k \right) = \sum\limits_{i = 1}^{{M_B}} {\sum\limits_{\begin{array}{*{20}{c}} {u \in Uj\left( n \right)}\\ {(i,u) \ne (m,k)} \end{array}} {{\mathit{\boldsymbol{P}}_{i,u}}\left( n \right)\mathit{\boldsymbol{h}}_{i,k}^{\rm{H}}\left( n \right){\mathit{\boldsymbol{h}}_{i,k}}\left( n \right)} } $ | (8) |
其中
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}_{i,u}}(n) = }\\ {\frac{{{\gamma _{{\rm{SINR}}j,u}}(n)}}{{1 + \sum\limits_{i = 1}^{{M_B}} {\sum\limits_{\begin{array}{*{20}{c}} {u \in U(n)}\\ {(i,u) \ne (m,k)} \end{array}} {\mathit{\boldsymbol{w}}_{i,u}^{\rm{H}}(n)\mathit{\boldsymbol{h}}_{i,k}^{\rm{H}}(n){\mathit{\boldsymbol{h}}_{i,k}}(n){\mathit{\boldsymbol{w}}_{i,u}}(n)} } }}} \end{array} $ | (9) |
其中,当服务于用户k∈Um(n)时,基站m对在时隙n其他同信道用户的干扰.通过选择梯度Λ(W, λ)对wm, k(n)等于零,得下面的等式集合[9-10]:
| $ \begin{array}{*{20}{c}} {\left( {{\mathit{\boldsymbol{L}}_{m,k}}(n) + {\mathit{\boldsymbol{\lambda }}_m}\ln 2{I_M}} \right){\mathit{\boldsymbol{w}}_{m,k}}(n) = }\\ {\frac{{\mathit{\boldsymbol{h}}_{m,k}^{\rm{H}}(n){\mathit{\boldsymbol{h}}_{m,k}}(n){\mathit{\boldsymbol{w}}_{m,k}}(n)}}{{1 + \mathit{\boldsymbol{w}}_{m,k}^{\rm{H}}(n)\mathit{\boldsymbol{h}}_{m,k}^{\rm{H}}(n){\mathit{\boldsymbol{h}}_{m,k}}(n){\mathit{\boldsymbol{w}}_{m,k}}(n) + {i_{m,k}}(n)}}} \end{array} $ | (10) |
等式集合式(10)与功率限制式(9),以及下面的互补slackness条件,形成了优化的一阶必要条件,即KTT条件:
| $ \begin{array}{*{20}{c}} {{\lambda _m}\left[ {{P_{m,\max }} - \sum\limits_{n = 1}^N {\sum\limits_{k \in {U_m}(n)} {\mathit{\boldsymbol{w}}_{n,k}^{\rm{H}}(n){\mathit{\boldsymbol{w}}_{n,k}}(n)} } } \right] = 0}\\ {m = 1,2, \cdots ,{M_B}} \end{array} $ | (11) |
这里K-T条件的迭代求解算法.
令Tm, k(n, λm)=Lm, k(n)+(λmln 2)IP,解决式(5)非凸问题的波束矢量具有如下形式[9, 11]:
| $ {\mathit{\boldsymbol{w}}_{m,k}}(n) = {\mathit{\boldsymbol{\beta }}_{m,k}}\left( {n;{\lambda _m}} \right)\mathit{\boldsymbol{T}}_{m,k}^ + \left( {n;{\lambda _m}} \right){\mathit{\boldsymbol{h}}_{m,k}}(n) $ | (12) |
其中:λm≥0, βm, k(n; λm)≥0是常数,仅当hm, k(n)∈{Lm, k(n)}, wm, k(n)≠0, λm=0有解.若wm, k(n)≠0,把式(12)代入式(10),对用户k∈Um(n)可得
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{h}}_{m,k}^{\rm{H}}(n)\mathit{\boldsymbol{T}}_{m,k}^ + \left( {n;{\lambda _m}} \right){\mathit{\boldsymbol{h}}_{m,k}}(n) = 1 + {i_{m,k}}(n) + }\\ {{{\left( {{\beta _{m,k}}\left( {n;{\lambda _m}} \right)\mathit{\boldsymbol{h}}_{m,k}^{\rm{H}}(n)\mathit{\boldsymbol{T}}_{m,k}^ + \left( {n;{\lambda _m}} \right){\mathit{\boldsymbol{h}}_{m,k}}(n)} \right)}^2}} \end{array} $ | (13) |
同理,把式(12)代入式(5),有
| $ \sum\limits_{m = 1}^N {\sum\limits_{k \in U(k)} {\left\| {{\beta _{m,k}}\left( {n,{\lambda _m}} \right)\mathit{\boldsymbol{T}}_{m,k}^ + \left( {n;{\lambda _m}} \right){\mathit{\boldsymbol{h}}_{m,k}}(n)} \right\|} } \le {\mathit{\boldsymbol{P}}_{m,max}} $ | (14) |
假定已有的可行矢量{wm, k(n)}给定,{im, k(n)}和{Lm, k(n)}可用式(7)和式(9)计算.定义x+=max(x, 0), {βm, k(n; λm)}的新值可以由式(13)计算如下:
| $ \begin{array}{*{20}{c}} {{{\left( {{\beta _{m,k}}\left( {n;{\lambda _m}} \right)} \right)}^2} = }\\ {\frac{{{{\left( {\mathit{\boldsymbol{h}}_{m,k}^{\rm{H}}(n)\mathit{\boldsymbol{T}}_{m,k}^ + \left( {n;{\lambda _m}} \right){\mathit{\boldsymbol{h}}_{m,k}}(n) - 1 - {i_{m,k}}(n)} \right)}^ + }}}{{{{\left( {\mathit{\boldsymbol{h}}_{m,k}^{\rm{H}}(n)\mathit{\boldsymbol{T}}_{m,k}^ + \left( {n;{\lambda _m}} \right){\mathit{\boldsymbol{h}}_{m,k}}(n)} \right)}^2}}}} \end{array} $ | (15) |
由式(14)和式(15)可用如下不等式计算新的值λm, 为
| $ \sum\limits_{n = 1}^N {\sum\limits_{k \in U(n)} {{f_{m,k}}} } \left( {n;{\lambda _m}} \right) \le {P_{m,\max }} $ | (16) |
定义
| $ {f_{m,k}}\left( {n,{\lambda _m}} \right) = {\mathit{\boldsymbol{h}}_{m,k}}\left( {n;{\lambda _m}} \right) - {i_{m,k}}{(n)^ + }{g_{m,k}}\left( {n;{\lambda _m}} \right) $ | (17) |
其中
| $ {\mathit{\boldsymbol{h}}_{m,k}}\left( {n;{\lambda _m}} \right) = \mathit{\boldsymbol{h}}_{m,k}^{\rm{H}}(n){\left[ {{\mathit{\boldsymbol{L}}_{m,k}}(n) + \lambda \ln 2{\mathit{\boldsymbol{I}}_P}} \right]^ + }{\mathit{\boldsymbol{h}}_{m,k}}(n) $ | (18) |
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{g}}_{m,k}}(n:\lambda ) = }\\ {\frac{{{{\left\| {{{\left[ {{\mathit{\boldsymbol{L}}_{m,k}}(n) + \lambda \ln 2{\mathit{\boldsymbol{I}}_P}} \right]}^ + }{\mathit{\boldsymbol{h}}_{m,k}}(n)} \right\|}^2}}}{{{{\left( {\mathit{\boldsymbol{h}}_{m,k}^{\rm{H}}(n)\left[ {{{\left[ {{\mathit{\boldsymbol{L}}_{m,k}}(n) + \lambda \ln 2{\mathit{\boldsymbol{I}}_P}} \right]}^ + }{\mathit{\boldsymbol{h}}_{m,k}}(n)} \right]} \right)}^2}}}} \end{array} $ | (19) |
在式(17)中fm, k(n; λm)是非负的,λm>0的非增函数,而且只要fm, k(n; λm)>0, fm, k(n; λm)是λm>0的严格递减函数,相关证明可以参阅相关文献.
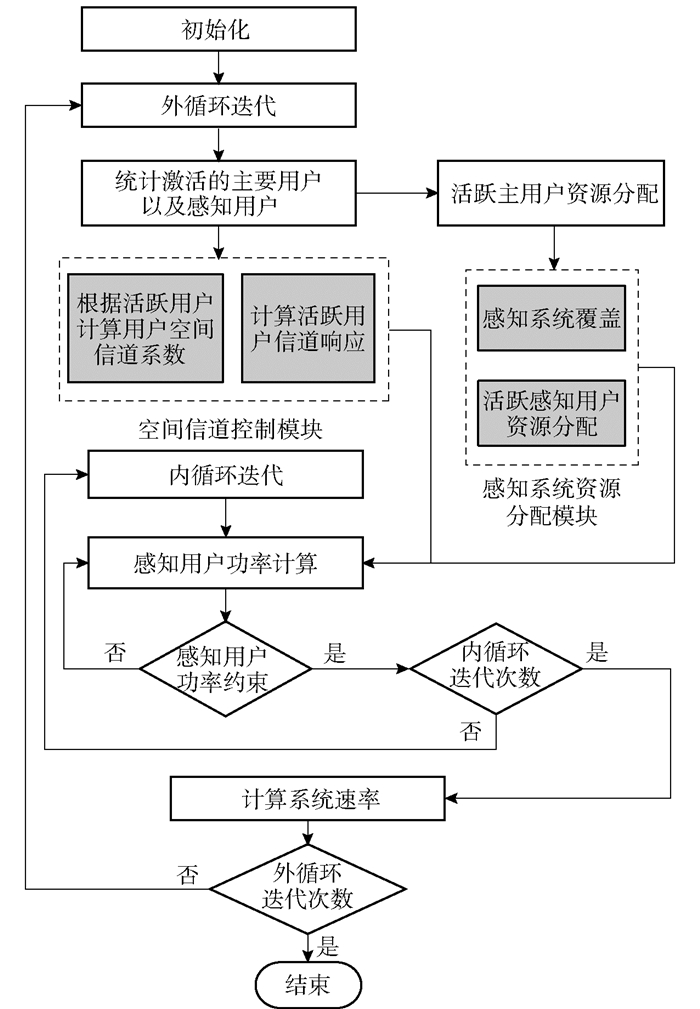
2 优化分配算法在资源优化分配算法上采用模块化设计,首先在空间信道控制模块第一步生成SU的信道,然后根据式(12)计算活跃用户的波束赋型控制系数.其次资源分配模块根据感知频谱资源为激活用户分配相应的资源,资源分配流程如图 2所示.
|
图 2 感知系统资源分配流程 |
1 初始化,初始解,功率可以在波束间均分‖wm, k(n)‖2=Pm, max/NK,忽略小区内和小区间干扰,简单选择初始的波束矢量匹配信道:
2 lout=0
3 while (lout < Lout-max)
4 根据式(8)计算Lm, k(n), k∈Um(n), m=1, …, BM, n=1, …, N}
5 lin=0
6 while (lin < Lin-max)
7 根据式(7)计算im, k(n), k∈Um(n),m=1, …, BM,n=1, …, N}.
8 For m=1:BM
9 根据式(11)和式(15)计算λm, βm, k(n; λm),k∈Um(n),m=1, …, BM,n=1, …, N}.
10 根据式(12)更新wm, k(n).
11 end
12 lin=lin+1
13 直到收敛或lin=Lin-max.
14 lout=lout+1
15 直到收敛或lout=Lout-max
2.2 感知系统资源分配算法1 初始化,基站数BM,用户数K.
2 统计活跃用户数K,依据瑞利衰落信道生成用户信道响应系数hactive_SU(k)=randn(NRx, NTx)+j randn (NRx, NTx),k=1, 2, …K.
3 For CN=1:BM
4 While (i < Max_Itera)
5 调用空间信道控制波束成型模块,根据式(12)wm, k(n)计算激活用户信道控制系数
| $ W = \left[ {{w_1}, \cdots ,{w_k}} \right] $ |
6 根据第5步,利用式(8)对SU用户进行功率资源分配.
7 根据式(5)计算感知系统速率.
8 直到第7中收敛或迭代结束.
9 i=i+1.
10 end.
3 仿真分析仿真平台为Matlab R2010b,仿真参数设置如表 1所示.
|
|
表 1 仿真参数设置 |
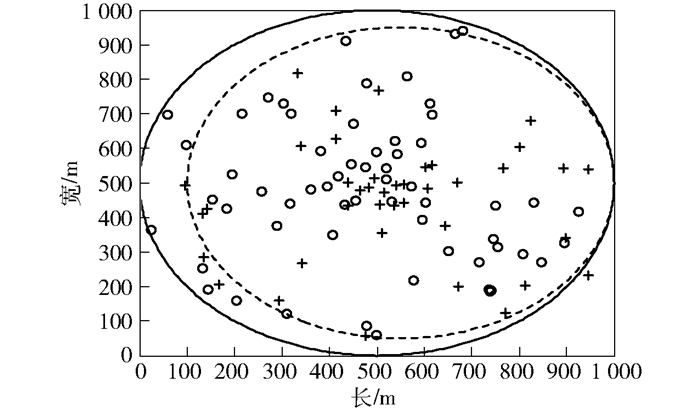
图 3中主要描述了授权基站和感知系统的覆盖区域是1 km×1 km,以及在任一时刻PUs和SUs的分布情况.红色圆为主用户系统基站覆盖区域,蓝色圆为感知系统基站覆盖范围.符号“O”表示活动的PUs分布,符号“+”表示活动的SUs.
|
图 3 主用户和次级用户分布 |
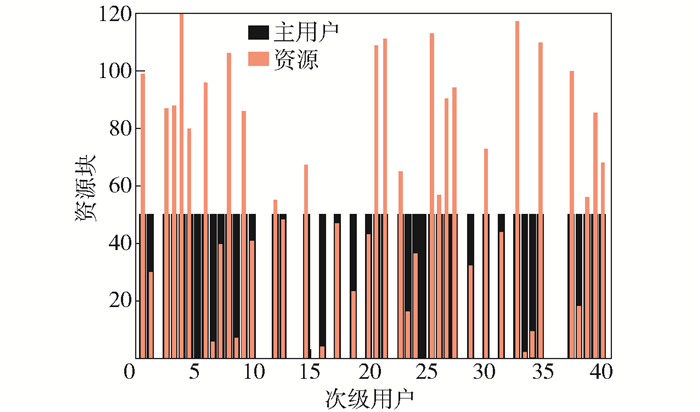
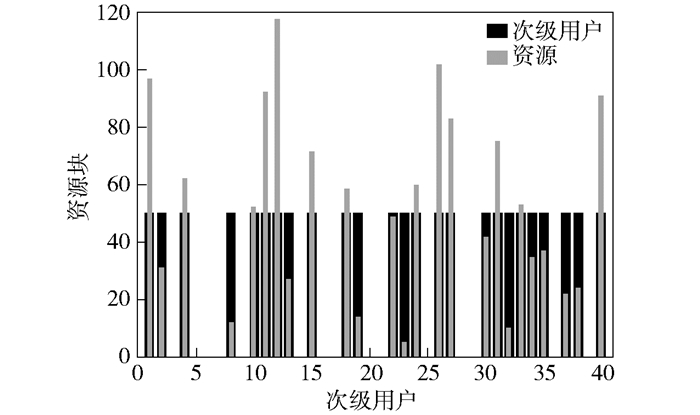
在图 4和图 5中,横坐标表示主要用户和次级用户,黑色条形图仅表示在某一时刻活跃的PUs和SUs,红色表示对活跃的用户分配资源,其纵坐标表示分得资源块标号.为表示资源是否被占用,本文中对所有的资源块进行了标号.比如主用户1使用标号为99资源块,主要用户3使用标号为87的资源块等.对于频谱感知系统要查找没有被占用的资源块分给请求资源分配的SUs.如图 4,次级用户1表示请求资源分配的SU,把空闲的97资源块分给SU1,62资源块分给了SU4等等.从图 4和图 5中可以看出,对于一个通信系统中,在一般条件下(不是满载)确实有大量的空闲频段没有被利用,这显然降低了宝贵资源频谱的利用效率,因而使用这些在瞬时没有被利用的频谱资源能够显著增加频谱的使用效率.
|
图 4 主用户资源分配 |
|
图 5 感知用户资源分配图 |
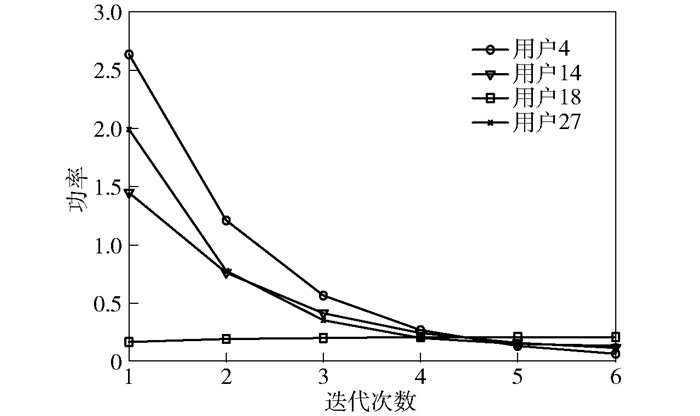
图 6仿真显示了本文算法中用户功率收敛特性.从仿真分析可以看出,本文算法能够使用户的功率快速收敛,一般迭代到6次都能够达到满足各用户工作的最低门限功率要求.
|
图 6 用户功率算法收敛性 |
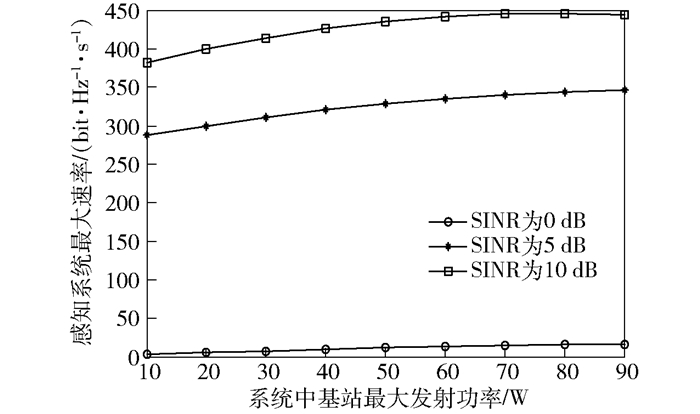
图 7仿真分析了系统在不同信噪比下感知系统中峰值速率(图 7中数据是50次运行叠加的平均值).从图 7中可以看出,当信噪比为0 dB情况下,系统速率较低.增加系统基站的发射功率,比如总功率从10 dBm增加到50 dBm(100 W),系统速率从3 bit·Hz-1·s-1增加到18 bit·Hz-1·s-1,而后增加系统发射功率,系统速率将逐步收敛.但当增加信噪比如5 dB时,系统速率将是0 dBm时3 bit·Hz-1·s-1的93倍达到280 bit·Hz-1·s-1.在继续增加信噪比达到10 dB时,系统速率比在5 dB时增加了大约100 bit·Hz-1·s-1.从图 7中也反映出系统在增加信噪比时能明显提升整个系统的性能,但增加基站发射功率达到50 dBm后,在增加发射功率系统性能改善不会明显增加而是逐渐收敛.这反映出基于空间信道控制的多天线感知系统对基站的发射功率反应不明显,而对系统信噪比有明显的效果.但在仿真过程中也出现了高传输功率条件下系统性能恶化的情况.由于图中的仿真结果是个平均值,没有反应出这一现象.笔者没有深入研究性能恶化的原因,只是对这一现象做了简单的推测.空间信道控制传输虽然能降低甚至消除用户间的干扰,而系统基站增加发射功率,只是改变传输功率却增加了用户背景热噪声功率,相应的增大了对用户的干扰,结果导致性能恶化.
|
图 7 系统吞吐量 |
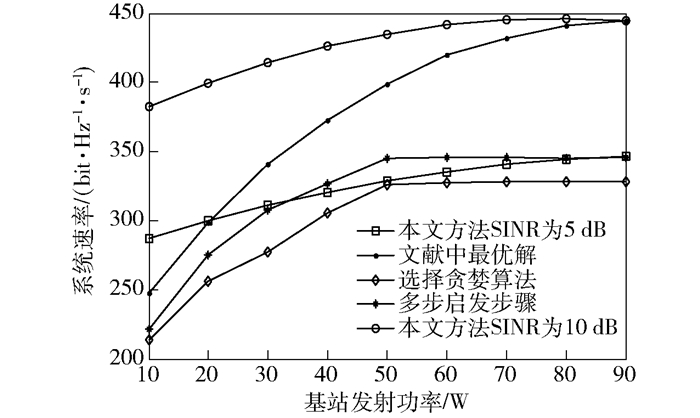
图 8仿真显示了本文方法与文献[6]方案的性能比较.结果显示,在高信噪比条件下, 如SNR为5 dB,基站发射功率为10 dBm时,本文方案的系统速率比文献[6]中贪婪选择算法下获得的系统速率高.当系统中基站功率继续增加50 dBm时,本文方案逐渐趋于文献中资源分配的选择贪婪算法和多步启发步骤算,但远远低于文献中方案的理论最优解.这说明本文算法在信噪比为5 dB时,系统性能可以趋于文献中多步启发步骤算法,稍好于文献中选择贪婪算法.
|
图 8 不同算法比较 |
当继续增加发射功率时文献中选择贪婪算法和多步启发步骤算法收敛于固定发射速率, 而本文方法也将收敛于文献多步骤启发算法的系统速率;当信噪比为10 dB,系统发射功率低于50 dBm时,本文方法明显优于文献中方案.当基站功率继续增加时,本文方法系统速率逐渐收敛并趋于文献方案的最优解.因而说本文方式在高信噪比条件下也能够较好发挥频谱感知系统的作用,且有更高的频谱利用效率.
4 结束语研究了基于多天线空间信道控制方式的频谱感知系统资源分配技术.通过多天线波束赋型技术,采用空间信道控制方式使发射天线的主瓣波束对准期望用户,让波束的零陷对准干扰用户,从而降低SU发射功率对PU的干扰进而提高系统的频谱利用效率.通过仿真分析,结果显示本文方案系统最大速率在信噪比为5 dB,基站发射总功率为10~90 dBm时趋于文献中方案中贪婪选择算法和多步启发步骤算法,而在信噪比为10 dB时,文中策略优于其他文献方案.
| [1] |
Xu W, Zhou X, Lee C H, et al. Energy-efficient joint sensing duration, detection threshold, and power allocation optimization in cognitive OFDM systems[J]. IEEE Transactions on Wireless Communications, 2016(99): 1-1. |
| [2] |
徐超.认知无线电网络中的安全中继选择与功率分配研究[D].北京邮电大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10013-1015583989.htm
|
| [3] |
Xu D, Li Q. Energy efficient joint scheduling and resource allocation for downlink cognitive radio networks[C]//International Conference on Wireless Communications & Signal Processing.[S.l.]: IEEE, 2015: 1-5.
|
| [4] |
马琳.基于OFDM的无线协同中继系统资源优化分配研究[D].北京: 北京邮电大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10013-1015584237.htm
|
| [5] |
Manna T, Misra I S. Joint optimization of detection thresholds and power allocation in OFDM based cognitive femtocell networks[C]//IEEE International Conference on Communication, Networks and Satellite.[S.l.]: IEEE, 2013: 69-73.
|
| [6] |
张碧玲.认知无线电网络中的频谱共享策略研究[D].北京邮电大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10013-1013326275.htm
|
| [7] |
Tervo O, Tran L N, Juntti M. Decentralized coordinated beamforming for weighted sum energy efficiency maximization in multi-cell MISO downlink[C]//IEEE Global Conference on Signal and Information Processing.[S.l.]: IEEE, 2016: 1387-1391.
|
| [8] |
Qiu Ling, Xu Jie, Liu Bei, et al. Multi-user multi-cell MIMO communication technology[M]. Beijing: Posts and Telecommunications Press, 2011: 129-131.
|
| [9] |
He S, Huang Y, Yang L. Coordinated beamforming for sum rate maximization in multi-cell downlink systems[J]. Signal Processing, 2014, 105(12): 22-29. |
| [10] |
Tervo O, Tran L N, Juntti M. Decentralized coordinated beamforming for weighted sum energy efficiency maximization in multi-cell MISO downlink[C]//IEEE Global Conference on Signal and Information Processing.[S.l.]: IEEE, 2016(1): 1387-1391.
|
| [11] |
Tong Z, Li B, Hui Y. Joint scheduling and beamforming for energy efficiency maximization in downlink coordinated multi-cell networks[J]. Wireless Personal Communications, 2015, 85(3): 1333-1350. DOI:10.1007/s11277-015-2843-y |


