2. 中国民航大学 中国民航信息技术科研基地, 天津 300300;
3. 民航旅客服务智能化应用技术重点实验室, 北京 101318;
4. 中山大学 机器智能与先进计算教育部重点实验室, 广州 510275
由于潜在高价值旅客当前乘机历史记录少,较难被航空公司准确发现并关注.对此,提出基于出行意图的潜在高价值旅客发现概率模型.首先建立一个基于统计的潜在高价值旅客发现概率模型,再将旅客出行意图引入概率模型,发现旅客潜在航线需求,优化旅客潜在价值计算,从而通过出行意图发现潜在高价值旅客.实验结果表明,相比于次数法、里程法以及RFM模型等传统的旅客价值度量方法,基于出行意图的潜在高价值旅客发现概率模型能够有效识别潜在高价值旅客.
2. Information Technology Research Base of Civil Aviation Administration of China, Civil Aviation University of China, Tianjin 300300, China;
3. Key Laboratory of Intelligent Passenger Service of Civil Aviation, Beijing 101318, China;
4. Key Laboratory of Machine Intelligence and Advanced Computing, Sun Yat-sen University, Guangzhou 510275, China
Potential high-value passengers can not be effectively discovered by airways due to the limited historical booking records of passengers. Aiming at this problem, a probabilistic model for discovering potential high-value passengers based on trip purposes mining is proposed. Firstly, we present a probabilistic model based on statistics to measure the value of passengers. Then, trip purposes are introduced into the model to discover potential airline demands of each passenger and to optimize passenger potential value calculation. Therefore, potential high-value passengers can be discovered through the trip purposes mining. Experiments show that the proposed model can identify the potential high-value passengers more accurately than the traditional passenger value evaluation methods based on the passengers' cumulative number of flight times, passengers' cumulative mileage and recency frequency monetry model.
传统的旅客价值度量方法有次数法、里程法以及RFM(recency frequency monetry)模型.这些方法仅利用旅客个体的历史出行数据,计算旅客当前实际产生的价值,把每位旅客当作彼此不相关联的独立实体.然而,在现实生活中,旅客基于一定的出行意图出行,出行意图客观存在,且被所有旅客共享,可以通过大规模旅客出行数据得到民航旅客出行背后隐藏的出行意图.准确发现每位旅客的出行意图分布可以预测旅客未来乘坐历史未乘坐航线的概率,进而发现旅客潜在航线需求.因此,旅客价值计算不能忽略旅客出行意图的影响. Lin Youfang等[1]通过旅客共同出行关系构建社交网络并生成基于社交网络的新特征,利用这些特征能够推断旅客群体的出行意图,但无法发现相同群体内不同旅客间出行意图的差别;王晶晶等[2]利用LDA(latent dirichlet allocation)模型发现城市交通旅客出行意图,根据旅客出行意图将旅客分类,由于没有考虑不同出行意图下旅客的潜在出行需求,无法发现当前历史记录少但增值潜力大的旅客;冯霞等[3]通过构建旅客航线异构网络,在起飞机场和目的机场间采用随机游走算法模拟旅客选择航线的行为,考虑了旅客潜在出行需求但忽略了旅客忠诚度对旅客价值的影响,无法区分潜在出行需求相同的旅客对特定航空公司的价值区别.
另一方面,对于当前乘机次数较少的旅客,没有历史数据预测旅客未来乘坐历史未乘坐航线的概率,存在“冷启动[4]”问题.传统的矩阵分解方法无法克服冷启动,而LDA主题模型利用先验概率模式克服此问题.因此,提出了一个基于出行意图的潜在高价值旅客发现概率模型.通过挖掘旅客出行意图来发现旅客对所有航线的潜在需求,更准确地计算旅客真实价值和潜在价值,从而发现当前乘机记录较少的潜在高价值旅客,避免了传统旅客价值度量方法对潜在高价值旅客的忽视.
笔者的主要贡献:1)考虑多种因素影响,提出概率模型预测潜在高价值旅客,并通过实验验证了模型框架的有效性;2)利用主题模型挖掘民航旅客出行意图,并通过实验得到最佳出行意图数;3)将主题模型引入旅客潜在价值计算,通过参数动态变化,根据不同旅客的出行意图分布预测旅客潜在航线需求,优化概率计算.
1 基于统计的潜在高价值旅客发现概率模型记u表示任一旅客,c表示特定航空公司,r表示航线,Rc为航空公司c所有航线的集合,Ru为旅客u历史出行航线的集合,做如下符号定义.
1) p(u):衡量旅客u乘机的先验信息,且
| $ p\left( u \right) = \frac{{旅客u乘机总次数}}{{{\rm{所有航空公司总的订票记录数}}}} $ | (1) |
2) p(c|u):衡量旅客u对航空公司c的忠诚度,且
| $ p\left( {c|u} \right) = \frac{{旅客u乘坐航空公司c的总次数}}{{{\rm{旅客}}u{\rm{历史乘机总次数}}}} $ | (2) |
3) p(c|r):衡量航空公司c在航线r∈Rc上的市场占有率,且
| $ p\left( {c|r} \right) = \frac{{航空公司c在航线r上开辟航班总数}}{{{\rm{当前所有航空公司在航线}}\mathit{r}{\rm{上开辟航班总数}}}} $ | (3) |
4) p(r|u):衡量旅客u的潜在航线需求.潜在航线需求反映旅客未来乘坐航线r∈Rc的可能性,即乘机潜力.旅客u对航线r∈Rc的需求为
| $ \left\{ \begin{array}{l} p\left( {r|u} \right) = \frac{{旅客u乘坐航线r总次数}}{{旅客u乘坐所有航线总次数}}, {\rm{ }}r \in {R_u}\\ 0, {\rm{ }}r \in {R_c} \wedge r \notin {R_u} \end{array} \right. $ | (4) |
使用概率p(u|c)度量旅客u对航空公司c的价值.其物理含义为给定航空公司c,根据旅客u对航空公司c的偏好以及对航线r∈Rc的潜在需求,旅客u选择航空公司c的可能性.对p(u|c)建模,得到基于统计的潜在高价值旅客发现概率模型:
| $ \begin{array}{l} p\left( {u|c} \right) = \lambda p\left( u \right)p\left( {c|u} \right) + \\ \left( {1 - \lambda } \right)p\left( u \right)\;\sum\limits_r {p\left( {r|u} \right)p\left( {c|r} \right)} \end{array} $ | (5) |
式(5)表示的旅客价值有当前价值p(u)p(c|u)和潜在价值
由于式(4)的计算基于旅客历史出行航线数据的统计,直接将旅客历史航线需求当作旅客未来潜在航线需求,预测旅客u对航线r∈Rc∧r∉Ru的未来乘机概率为0,于是,在式(5)的旅客潜在价值部分有:
| $ p\left( u \right)\;\sum\limits_r {p\left( {r|u} \right)p\left( {c|r} \right)} {\rm{ }}\left\{ \begin{array}{l} \ne 0, r \in {R_u}\\ = 0, r \in {R_c} \wedge r \notin {R_u} \end{array} \right. $ | (6) |
然而,旅客历史航线需求并不能完全客观反映旅客潜在航线需求.首先,即使不同旅客乘坐同一条航线次数相等,也不能简单的认为旅客对这条航线的需求完全相同,且旅客未来对航线的需求并不一定与历史乘坐航线r∈Ru需求完全一致;其次,旅客对航线r∈Rc∧r∉Ru的未来乘机需求概率也不会恒为0.因此,式(5)给出的基于统计的潜在高价值旅客发现概率模型无法准确计算旅客的潜在价值.
2 基于出行意图的潜在高价值旅客发现概率模型 2.1 模型建立通过引入旅客出行意图发现旅客的潜在航线需求,优化旅客价值的计算,可以准确识别潜在高价值旅客.从旅客出行角度来讲,出行意图是旅客选择某条航线出行的动机.引入出行意图,旅客的一次出行可表述为2个阶段:旅客以一定的概率基于某意图出行和基于该出行意图选择某条出行航线.在忽略旅客的出行具体动机,而给出出行意图个数时,可通过旅客历史出行航线,得到旅客的出行意图分布.从航线角度看,相同出行意图下不同航线出现的概率不同.不同出行意图下,同一条航线出现的概率也不同.于是,可以通过所有旅客历史出行航线去发现不同出行意图下的所有航线分布.
设旅客历史出行数据中包含M位旅客以及V条航线,z表示旅客出行意图,旅客出行基于K个出行意图.记p(z|u)为旅客u选择出行意图z的概率,p(r|z)为航线r基于出行意图z出现的概率.于是,在基于统计的潜在高价值旅客发现概率模型中,旅客潜在航线需求p(r|u)的计算可表示为
| $ p\left( {r|u} \right) = n\sum\limits_k {p\left( {r|z} \right)p\left( {z|u} \right)} $ | (7) |
| $ \sum\limits_k {p\left( {z = k|u} \right)} = 1 $ | (8) |
其中:当r∈Ru,n表示旅客历史乘坐航线r的次数;当r∈Rc∧r∉Ru,n=1.通过n的动态变化,不但加入旅客历史乘坐航线r∈Ru的先验信息,也为计算旅客对于r∈Rc∧r∉Ru的需求提供了方法.
M位旅客出行意图分布构成M×K阶矩阵θ,θ中每一行θu表示旅客u的出行意图分布,所有出行意图下航线分布构成K×V阶矩阵φ.于是,
| $ p\left( {r|u} \right) = n{\mathit{\boldsymbol{\theta }}_u}\mathit{\boldsymbol{\varphi }} = n\sum\limits_{i = 1}^K {{\mathit{\boldsymbol{\theta }}_{u, i}}{\mathit{\boldsymbol{\varphi }}_{i, r}}} $ | (9) |
此时,由于不同旅客出行意图分布不同,可以区分乘坐某航线次数相同的旅客对该航线的不同需求.通过旅客u的出行意图分布θu以及不同出行意图下航线分布φ,可以根据式(9)计算出旅客基于不同出行意图对航线r∈Rc的潜在需求.对于旅客u的历史出行中不存在的航线r′,即r′∈Rc∧r′∉Ru,由于p(c|r′)≠0,
| $ p\left( u \right)p\left( {r\prime |u} \right)p\left( {c|r\prime } \right) \ne 0 $ | (10) |
于是,得到式(6)的改进表达形式如下:
| $ \begin{array}{l} p\left( u \right)\sum\limits_r {p\left( {r|u} \right)p\left( {c|r} \right)} {\rm{ }}\\ \;\;\;\left\{ \begin{array}{l} \ne 0, r \in {R_u}\\ \ne 0, r \in {R_c} \wedge r \notin {R_u} \end{array} \right. \end{array} $ | (11) |
由式(11)可知,引入出行意图的潜在高价值旅客发现概率模型优化了旅客潜在价值的计算,代入式(5)可以更准确地计算旅客价值,从而构成基于出行意图的潜在高价值旅客发现概率模型.
2.2 模型参数求解基于出行意图的潜在高价值旅客发现概率模型的求解关键是获得所有旅客历史出行航线中每条航线对应的出行意图,从而计算得到旅客出行意图分布矩阵θ以及所有出行意图下航线分布矩阵φ.
设旅客的出行意图分布符合以α为参数的K维狄利克雷分布Dir(α),其中α的每一维值均为α;以多项式概率抽取旅客出行意图,不同出行意图下的航线分布符合以β为参数的V维狄利克雷分布Dir(β),其中β的每一维值均为β.
每位旅客的所有历史出行航线构成该旅客的航线文档,所有旅客的航线文档构成整个语料库,每位旅客的每条历史出行航线占用语料库中一个位置.考虑出行航线对于出行意图的后验概率p(z|r),采用Gibbs抽样算法求解旅客历史出行航线中每条航线的出行意图.
设ri表示语料库中第i个位置对应的航线,
| $ \begin{array}{l} p({z_i} = j|{\mathit{\boldsymbol{z}}_{\tilde i}}, {\mathit{\boldsymbol{r}}_{\;\tilde i}}, {r_i}, \alpha , \beta ) \propto \\ \;\frac{{n_{u, \tilde i}^{(j)} + \alpha }}{{\sum\limits_{s = 1}^K {n_{u, \tilde i}^{(\mathit{s})}} + \mathit{K\alpha }}}\;\;\frac{{t_{j, \tilde i}^{({\mathit{r}_i})} + \beta }}{{\sum\limits_{r = 1}^V {t_{j, \tilde i}^{(\mathit{r})}} + \mathit{V\beta }}} \end{array} $ | (12) |
综上,求解旅客出行意图矩阵θ和所有出行意图下航线分布矩阵φ的步骤可归纳如下:
步骤1 初始化α, β,随机抽取每条航线的出行意图z,构造马尔可夫链的初始状态;
步骤2 根据式(12)抽取航线文档中一条历史出行航线的出行意图;
步骤3 重复步骤2,逐条抽取语料库中所有航线文档的每条航线的出行意图,一次迭代结束;
步骤4 重复步骤2~步骤3,多次迭代后,抽样样本开始接近目标概率分布,可求得航线文档中每条航线对应的出行意图.
步骤5 计算θu, j和φj, r,且
| $ {\mathit{\boldsymbol{\theta }}_{u, j}} = \frac{{n_u^{(j)} + \alpha }}{{\sum\limits_{s = 1}^K {n_u^{(\mathit{s})} + \mathit{K\alpha }} }} $ | (13) |
| $ {\mathit{\boldsymbol{\varphi }}_{j, r}} = \frac{{t_j^{({\mathit{r}_i})} + \beta }}{{\sum\limits_{r = 1}^V {t_j^{(\mathit{r})}} + \mathit{V\beta }}} $ | (14) |
最终得到矩阵θ和φ.
3 实验结果与分析 3.1 实验设置 3.1.1 实验数据集实验采用中国民航订票系统中2010年1月—2011年12月的真实订票数据.数据预处理后共有971条航线.实验中,通过概率模型发现2010年数据集中的潜在高价值旅客,并用2011年数据集作为验证集进行验证.采用比较两个集合之间的相似性与差异性的Jaccard系数来评价实验效果.
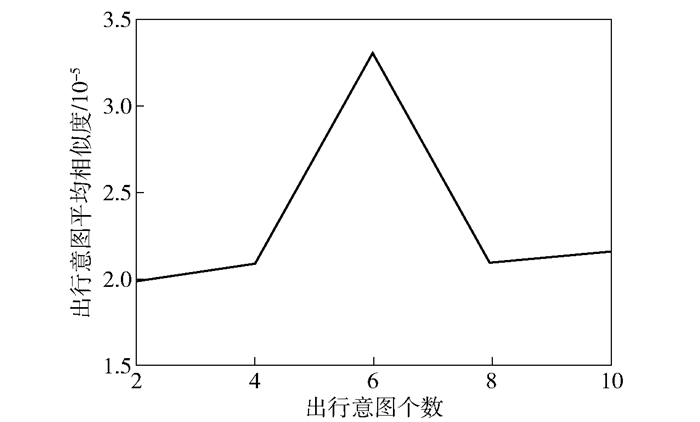
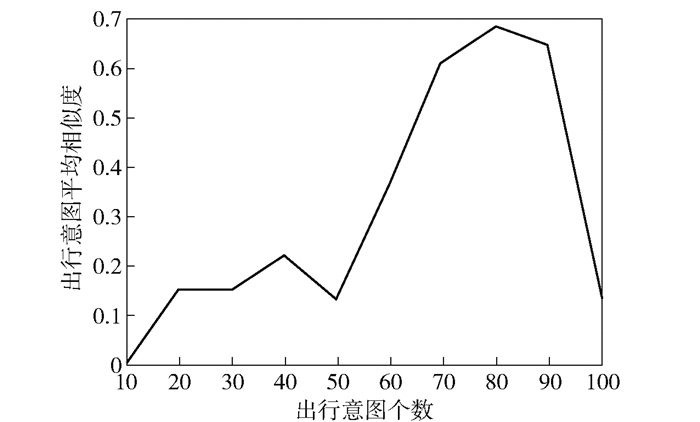
3.1.2 模型参数设置基于出行意图的潜在高价值旅客发现概率模型(后文简称基于出行意图的概率模型),需设定超参数α, β以及出行意图个数K. α, β取值α=50.0/K,β=0.01[5-8]. K表示旅客出行意图的数目,无法直接观测.为获得最优K值,采用余弦距离度量不同出行意图的相似度,当出行意图间的平均相似度最小时,分类最好,对应的K值最优[9].取不同步长不同K值分别进行旅客出行意图平均相似度实验(见图 1和图 2),可知当旅客出行意图个数K=2时,旅客出行意图平均相似度最小.
|
图 1 不同K(步长为2)下出行意图平均相似度变化 |
|
图 2 不同K(步长为10)下出行意图平均相似度变化 |
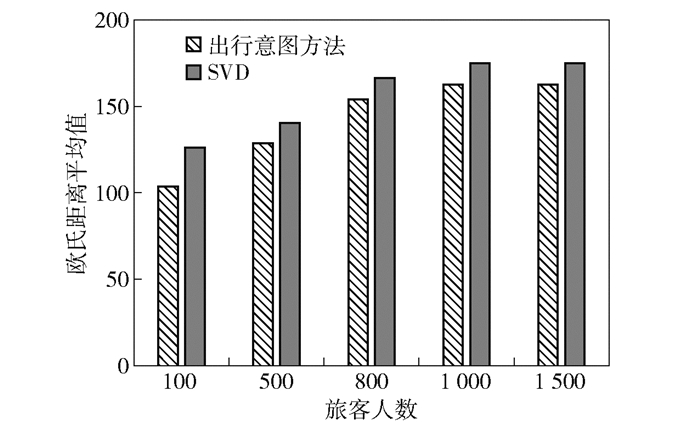
为了验证出行意图能优化旅客潜在航线需求计算,分别用所提利用出行意图计算潜在航线需求方法与传统矩阵分解方法SVD进行对比.统计2011年旅客对各航线的真实需求,比较不同方法预测旅客潜在航线需求向量与旅客真实航线出行向量的平均欧氏距离,实验结果见图 3.
|
图 3 出行意图方法与SVD分解对比 |
由图 3看出,利用出行意图预测旅客潜在航线需求向量与真实旅客航线出行向量的平均欧式距离明显小于SVD方法.验证了通过旅客出行意图挖掘可以优化旅客的潜在航线需求计算,进而优化旅客价值计算.
3.3 潜在高价值旅客发现实验比较与分析实验1 基于统计的概率模型与次数法、里程法以及RFM模型比较
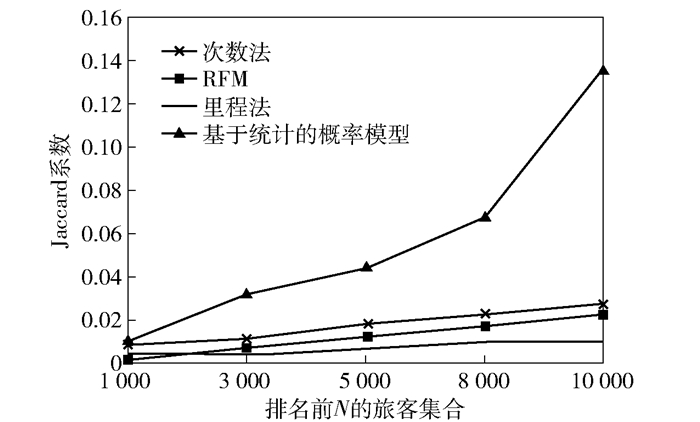
分别用基于统计的概率模型,次数法,里程法以及RFM模型计算得到2010年旅客价值排名前N(N=1 000, 2 000, 5 000, 8 000……)的旅客集合.再统计得到2011年旅客真实价值有序表,截取真实价值降序表排名前N的旅客集合,比较这2个集合的Jaccard相似性系数.实验结果见图 4:当N=10 000时,基于统计的概率模型Jaccard系数为0.137,明显高于次数法,里程法和RFM模型.与次数法相比,基于统计的概率模型得到的高价值旅客集合与真实高价值旅客集合的相似性系数提高了0.11.即使当N=1 000时,基于统计的概率模型的Jaccard系数可达到0.009 59,而次数法仅为0.008 06,可见基于统计的概率模型得到的高价值旅客集合与真实高价值旅客集合相似性系数更高.
|
图 4 基于统计的概率模型与相关方法的对比结果 |
之所以基于统计的概率模型能获得更高的Jaccard系数,是由于次数法和里程法仅利用旅客先验信息单一因素计算旅客价值,没有考虑旅客的潜在价值,模型粗糙,无法准确评估旅客价值.而基于统计的概率模型通过真实价值和潜在价值两个角度综合计算旅客价值,对旅客价值的计算更准确.
实验2 基于出行意图的概率模型与基于统计的概率模型以及基于随机游走的潜在高价值旅客发现比较
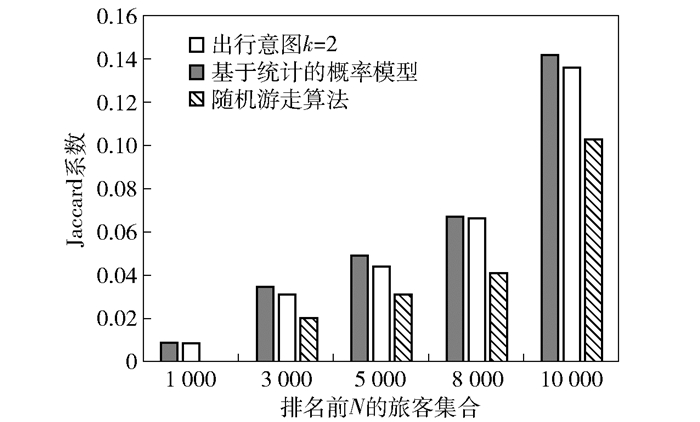
选取基于统计的概率模型与基于出行意图的概率模型以及随机游走算法进行对比,实验结果如图 5所示.其中,当N=10 000,K=2时,基于出行意图的概率模型得到的高价值旅客集合与真实高价值旅客集合Jaccard相似性系数为0.143 2,比基于统计的概率模型得到的高价值旅客集合与真实高价值旅客集合的Jaccard相似性系数提高了0.006.比随机游走算法高0.037 7.当N=1 000,K=2时,基于出行意图的概率模型得到的高价值旅客集合与真实高价值旅客集合的相似性系数为0.009 6,比基于统计的概率模型得到的高价值旅客集合与真实高价值旅客集合的Jaccard相似性系数提高了0.000 1,比随机游走算法高0.006 2.基于出行意图的概率模型可以通过出行意图计算旅客对所有航线的潜在需求,其潜在价值计算比基于统计的概率模型更加精细准确.随机游走算法忽略了特定航空公司的航线开辟情况以及旅客对特定航空公司的忠诚度影响,导致计算得到的潜在高价值旅客真实需求较大的航线并不是航空公司的主要执飞航线.
|
图 5 基于出行意图(k=2)的概率模型与相关算法的对比 |
为了避免潜在高价值旅客当前乘机次数少而无法被基于历史记录的旅客价值度量方法所发现,提出了基于出行意图挖掘的潜在高价值旅客发现概率模型.首先提出基于统计的潜在高价值旅客发现概率模型,然后通过挖掘旅客出行意图发现旅客的潜在航线需求,优化旅客潜在价值的计算,建立基于出行意图挖掘的潜在高价值旅客发现概率模型.最后在中国民航订票系统数据集上对基于出行意图的潜在高价值旅客发现概率模型进行旅客价值计算,并与真实情况实验验证和分析对比.实验结果表明,选取旅客价值降序表排名前1万名的旅客集合,基于统计的潜在高价值旅客发现概率模型比传统的旅客价值度量方法如次数法的Jaccard相似性系数提高了0.11.当出行意图个数为2,基于出行意图的潜在高价值旅客发现概率模型比基于统计的潜在高价值旅客发现概率模型Jaccard相似性系数提高了0.006.
| [1] |
Lin Youfang, Wan Huaiyu, Jiang Rui, et al. Inferring the travel purposes of passenger groups for better understanding of passengers[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(1): 235-243. DOI:10.1109/TITS.2014.2329422 |
| [2] |
Wang Jingjing, Chen Xi, Chen Zhihong, et al. Cluster algorithm based on LDA model for public transport passengers' trip purpose identification in specific area[C]//Proceedings of the 2016 IEEE International Conference on Intelligent Transportation Engineering (ICITE). Washington DC: IEEE, 2016: 186-192.
|
| [3] |
Feng Xia, Xu Bingyu, Lu Min, et al. Potential high-value passengers discovery by random walk on passenger-route heterogeneous network[J]. Journal of Computational and Theoretical Nanoscience, 2015, 12(8): 2217-2222. |
| [4] |
于洪, 李俊华. 一种解决新项目冷启动问题的推荐算法[J]. 软件学报, 2015, 26(06): 1395-1408. Yu Hong, Li Junhua. Algorithm to solve the cold-start problem in new item recommendations[J]. Journal of Software, 2015, 26(06): 1395-1408. |
| [5] |
曹建平, 王晖, 夏友清, 等. 基于LDA的双通道在线主题演化模型[J]. 自动化学报, 2014, 40(12): 2877-2886. Cao Jianping, Wang Hui, Xia Youqing, et al. Bi-path evolution model for onlinetopic model based on LDA[J]. ACTA Autmatic Sinica, 2014, 40(12): 2877-2886. |
| [6] |
郭蓝天, 李扬, 慕德俊, 等. 一种基于LDA主题模型的话题发现方法[J]. 西北工业大学学报, 2016, 34(4): 698-702. Guo Lantian, Li Yang, Mu Dejun, et al. A LDA model based topic detection method[J]. Journal of Northwestern Polytechnical University, 2016, 34(4): 698-702. |
| [7] |
谢昊, 江红. 一种面向微博主题挖掘的改进LDA模型[J]. 华东师范大学学报(自然科学版), 2013(6): 93-101. Xie Hao, Jiang Hong. Improved LDA model for microblog topic mining[J]. Journal of East China Normal University (Natural Science), 2013(6): 93-101. |
| [8] |
Blei D M, Ng A Y, Jordan M I. Latent dirichlet allocation[J]. The Journal of Machine Learning Research, 2003, 3(3): 993-1022. |
| [9] |
曹娟, 张勇东, 李锦涛, 等. 一种基于密度的自适应最优LDA模型选择方法[J]. 计算机学报, 2008, 31(10): 1780-1787. Cao Juan, Zhang Yongdong, Li Jintao, et al. A method of adaptively selecting best LDA model based on density[J]. Chinese Journal of Computers, 2008, 31(10): 1780-1787. DOI:10.3321/j.issn:0254-4164.2008.10.012 |


