提出了一种基于无率码的信息安全可靠传输方案,在编码器和译码器中设置伪随机数发生器,产生随机的编码生成矩阵和删除图案,实现编码符号的随机产生和随机删除.伪随机数发生器的种子就是加解密的密钥.由于随机删除后编码符号的度分布未改变,无率码的纠错性能不受影响.在加性高斯白噪声信道和瑞利衰落信道下的仿真结果表明,窃听者译码的误比特率保持在0.5附近,误字率保持为1;而合法接收者的差错性能则与常规的无率码编码系统相同,实现了纠错和保密的功能.
A secure and reliable transmission scheme based on rateless codes is proposed. The encoder and decoder generete random coding matrix and deleting pattern by setting up pseudo-random number generators, enabling random generation and deletion of encoded symbols, and the seed of pseudo-random number generator is the secret key. Since the degree distribution of the encoded symbols after random deletion is not changed, the error correction performance of the rateless codes is not affected. Simulation under additive white Gaussian noise channel and Rayleigh fading channel indicates that the bit-error-rate of the eavesdropper is kept near 0.5, and the word-error-rate remains 1, while the error performance of the legitimate receiver is the same as conventional rateless coding systems, thus error correction and encryption are realized simultaneously.
物理层安全是利用无线信道特性,通过调制、编码、信号处理等方法来实现信息论意义上的信息安全传输.其中一个重要的研究方向是利用信道编码同时实现信息的可靠和安全传输. McEliece提出基于Goppa码的公钥密码体制(M公钥体制)[1],首次利用纠错码实现了信息加密,其安全性在于它隐藏了进行快速译码时需要的Goppa码的编码矩阵(私钥),而在不知道私钥时,由公钥解出保密信息是一个NP完全问题.该方案的缺点是密钥开销大,码率低,且未考虑有扰信道.随后,出现了基于各种纠错码实现纠错和加密的方案.例如基于Turbo码[2]、卷积码[3]、QC-LDPC码[4]等的联合纠错加密方案,但这类方案往往在安全性、可靠性和复杂性之间存在折中.
给出一种利用无率码编码过程的随机性和译码过程的互信息累积性的安全可靠传输方案.无率码作为纠错码使用,在保证合法接收者译码不受影响的同时,确保窃听者在无密钥的情况下其译码的误比特率为0.5、误字率为1,保证了信息的安全.此外,还进一步增加了随机删除环节来提高安全性能.
1 无率码简介 1.1 Raptor码的编码无率码中常用作纠错码的是Raptor码. Raptor码先用一种纠错码作为外码进行预编码,再进行LT编码.具体过程如下.
1) 将K个输入符号sk(k=1, 2, …, K)经过预编码器编码得到M个中间符号um(m=1, 2, …, M).
2) 根据度分布ρ(d)产生一个随机度值dn(n= 1, 2, …, N),该随机数即为该编码符号的度值.度分布ρ(d)为任一编码符号度值为d的概率,度值为与某个编码节点相连的边数值.
3) 从M个中间符号随机等概地选择dn个符号,以这dn个符号的序号作为索引,将一个M维列矢量中索引指示的位置置为1,其余位置置为0,得到的矢量gn(n=1, 2, …, N)即为对应该编码符号的编码生成列矢量.
4) 对选定的dn个符号进行异或运算,运算结果即为Raptor码的一个编码符号cn(n=1, 2, …, N),即
| $ {c_n} = \mathit{\boldsymbol{u}}{\mathit{\boldsymbol{g}}_n} $ | (1) |
其中u=(u1, u2, …, uM)为中间符号组成的行矢量.
5) 重复执行步骤2)~4),直到产生了设定数量的编码符号,或收到接收端停止编码的反馈为止.
一个码字的编码完成后,所有编码符号进行LT编码时对应的编码生成矢量就构成当前码字的LT码生成矩阵G. LT编码器的输出可以看作M个符号构成的行矢量与编码生成矩阵G相乘得到,即
| $ \mathit{\boldsymbol{c}} = \mathit{\boldsymbol{uG}} $ | (2) |
其中c=(c1, c2, …, cN)为编码符号组成的行矢量.
1.2 Raptor码的译码Raptor码的译码过程分为以下2步:
1) 利用置信传播(BP, belief propagation)算法对接收到的数据进行LT译码,输出中间符号的软信息;
2) 将步骤1)中LT译码输出的软信息作为初始软信息,利用BP算法进行LDPC码的译码.
定义Lnc→f为由编码节点cn到校验节点fn的似然比信息,Lm, nu→f为由信息节点um到校验节点fn的似然比信息,Ln, mf→u为由校验节点fn到信息节点um的似然比信息. LT译码的具体过程如下:
1) 初始化
| $ \left. \begin{array}{l} L_n^{c \to f} = \log \frac{{p\left( {{c_n} = 0\left| {{y_n}} \right.} \right)}}{{p\left( {{c_n} = 1\left| {{y_n}} \right.} \right)}}\\ L_{n,m}^{f \to u} = 0\\ L_{m,n}^{u \to f} = 0 \end{array} \right\} $ | (3) |
其中:p(cn=0|yn)和p(cn=1|yn)分别表示接收端收到yn后cn为0和1的概率,yn(n=1, 2, …, N)表示cn经过信道传输后接收端接收到的符号.
2) 软信息的更新
| $ \left. \begin{array}{l} L_{n,m}^{f \to u} = 2{\tanh ^{ - 1}}\left( {\tanh \left( {\frac{{L_n^{c \to f}}}{2}} \right)\prod\limits_{m' \in {A_{n\backslash m}}} {\tanh \left( {\frac{{L_{m',n}^{u \to f}}}{2}} \right)} } \right)\\ L_{m,n}^{u \to f} = \prod\limits_{n' \in {B_{m\backslash n}}} {L_{n',m}^{f \to u}} \end{array} \right\} $ | (4) |
其中:An\m为除信息节点um外,与校验节点fn相连的所有信息节点的集合;Bm\n为除校验节点fn外,与信息节点um相连的其他所有校验节点的集合.
3) 判断迭代次数是否达到设定值,若达到,就进行软判决,输出各个信息节点的似然比信息Lmf→u;否则,就重复步骤2)和3)继续进行迭代.
| $ L_m^{f \to u} = \prod\limits_{n \in {B_m}} {L_{n,m}^{f \to u}} $ | (5) |
其中Bm为与信息节点um相连的所有校验节点的集合.
2 联合纠错保密方案及性能分析 2.1 基于无率码的联合纠错保密方案从第1节中LT码编译码过程可见,LT码的编码过程是随机的,即其编码矩阵是在编码过程中随机产生的.译码器正确译码的基础是要有相同的编码矩阵.在LT码作为纠删编码使用时,一个编码符号是一个数据帧,可以将与该编码符号相关的编码信息放在帧头同时传输.而LT码作为纠错编码使用时,一个编码符号是一个比特,显然不可能采用类似的编码信息传输方式.本文方案中,发送端(编码器)和接收端(译码器)以伪随机的方式同步产生编码矩阵,编码器和译码器的伪随机数发生器的种子则是密钥.作为一个完整的物理层保密方案,密钥可以利用合法信道的特性,用物理层的方法在发送端和接收端同步产生,当然也可以由一方产生,然后通过专门的保密信道共享.密钥的物理层产生方法可参考文献[5],笔者重点在于介绍用无率码实现保密和纠错的方案,因此不对此进行介绍.
编码器有2个伪随机数发生器,产生一个编码符号时,一个发生器先按度分布要求随机产生一个度值dn,另一个发生器则根据该度值在[1, M]间等概随机产生dn个的互不相同的整数值,这dn个整数作为序号用来选定参与该编码符号生成运算的中间符号.将长为M的列矢量中对应这些整数序号位置的元素置为1,其他元素置为0,就得到对应该编码符号的编码生成矢量.将该矢量与中间符号矢量相乘即得到一个编码符号.
译码器同样有2个伪随机数发生器,只要拥有与编码器伪随机数发生器相同的种子,就能与编码器同步产生相同的编码生成矢量.译码器在收到一定长度的编码符号后,根据这些编码符号对应的编码矢量组成的编码生成矩阵进行BP译码.
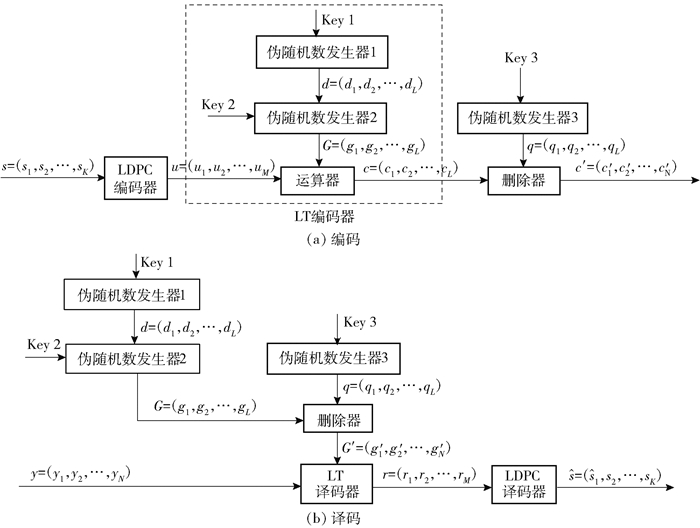
为了增强信息传输的安全性,在编码过程中增加一个随机删除环节.为此在编码器中另设置一个伪随机数发生器,采用另一个密钥作为种子,产生随机的0、1序列作为删除图案,记作q,q=(q1, q2, …, qL),L为删除图案的长度.随机删除器根据删除图案对LT码的编码符号进行删除,删除图案中对应位置为0就删除该编码符号,为1就保留. LT码编码器持续产生编码符号,直到删除器输出的符号数达到要求的长度N.编码器的结构和编码过程如图 1(a)所示.
|
图 1 保密方案编译码示意图 |
类似于编码矩阵的产生,译码器也需要与编码器同步产生错误图案,需要设置一个产生删除图案的伪随机数发生器.由于编码器将对应删除图案中为0的符号删除,译码时该符号就不应参加BP译码中的消息传递,因此译码器需要根据删除图案将编码生成矩阵中已删除符号对应的编码生成矢量删除,得到正确的编码生成矩阵G′=(g′1, g′2, …, g′N),然后再进行LT码的译码.译码过程如图 1中(b)所示.其中,3个伪随机数发生器分别用来产生随机度值、用来产生参加异或运算的符号序号以及用来产生伪随机删除图案. y=(y1, y2, …, yN)表示接收端接收到的符号组成的矢量,r=(r1, r2, …, rM)表示LT译码后输出的软信息组成的矢量,
码长一定时,Raptor码的纠错性能由预编码和LT码的度分布决定.本文方案中,采用伪随机的方法产生编码符号的度值及选择参与编码的中间符号,只要伪随机数发生器设计合理,周期足够长,就能非常逼近设计的度分布和中间符号选择的随机性.而编码后引入的随机删除环节也不改变编码的度分布,因此Raptor码的纠错性能没有改变.下面证明随机删除不改变LT码编码符号的度分布.定义Pe∈(0, 0.5]为每个编码符号被删除的概率,Pd为编码符号取各度值的概率.
设N为编码符号数,当N足够大时,度值为d的编码符号个数为NPd.以概率Pe随机删除后剩下的编码符号总数为N(1-Pe).由于编码符号间是否删除是相互独立的,所以度值为d的符号被删除的概率也是Pe,删除后剩下的编码符号中度值为d的符号个数为NPd(1-Pe).在删除后剩下的编码符号中,度值为d的符号数与总符号数的比值为
| $ \frac{{N{P_{\rm{d}}}\left( {1 - {P_{\rm{e}}}} \right)}}{{N\left( {1 - {P_{\rm{e}}}} \right)}} = {P_{\rm{d}}} $ | (10) |
也即经过删除后发送的编码符号中,度值为d的概率仍是Pd,删除前后的度分布并未发生变化.
2.2.2 安全性分析由1.2节所述LT码的译码过程可知,译码的关键在于软信息的计算及其迭代更新,而软信息的更新关系是由编码生成矩阵决定.因此,如果没有正确的编码生成矩阵,即使其接收信号质量很高,译码器也不能正确译码.还采用了随机删除编码符号的方式进一步增强安全性能,此时,窃听者即使知道编码生成矩阵,但若不能同时获得删除图案,也无法获得删除后的编码生成矩阵,也就不能正确译码.窃听者能否正确译码就取决于其能否获得正确的编码生成矩阵和删除图案.
本文方案是基于密钥和信道编码的保密体制,假设窃听者知道无率码的编码方法、度分布及随机删除的概率,但不知道编码生成矩阵和删除图案.对窃听者来说,有2种破解方法:第1种是根据编码度分布和删除概率随机产生编码生成矩阵和删除图案,尝试进行译码;第2种是尝试不同的密钥以获得正确的编码生成矩阵和删除图案用于译码.
先考虑没有进行编码符号随机删除的情况.对于一个M×N的LT码的编码生成矩阵,每一列为对应一个编码符号的M维编码生成矢量.编码生成矢量是由两个伪随机数发生器产生的伪随机数决定的,因此窃听者与编码器产生的编码生成矢量相同的概率即为按照度分布ρ(d)产生相同的度值并选定相同的源符号的概率,即
| $ {P_{\rm{c}}} = \sum\limits_{d = 1}^{{d_{\max }}} {\frac{{P_{\rm{d}}^2}}{{C_M^d}}} $ | (11) |
其中CMd为组合数.而一个生成矩阵有N个编码生成矢量,因此窃听者产生与编码器相同的编码生成矩阵的概率为
| $ {P_{\rm{g}}} = P_{\rm{c}}^N $ | (12) |
下面以本文仿真中采用的Raptor码为例来说明.仿真中LT码编码采用的度分布为
| $ \begin{array}{*{20}{c}} {\rho (x) = 0.008{x^1} + 0.493{x^2} + 0.166{x^3} + 0.073{x^4} + }\\ {0.083{x^5} + 0.056{x^8} + 0.037{x^9} + 0.056{x^{19}} + }\\ {0.025{x^{65}} + 0.003{x^{66}}} \end{array} $ | (13) |
当N=19 000时,计算可得Pc=1.126 2×10-8,Pg=PcN=4.953 8×10-151 020.可见,窃听者通过随机产生的方式得到与发送端一致的编码生成矩阵的概率几乎为0.
在有随机删除的情况下,窃听者即使获得了编码生成矩阵,但若不知道删除图案也不能正确译码.删除图案是长为N/(1-Pe)的0、1序列.窃听者与编码器删除图案中的一个比特相同的概率为
| $ {P_{\rm{s}}} = P_{\rm{e}}^2 + {\left( {1 - {P_{\rm{e}}}} \right)^2} = 2P_{\rm{e}}^2 - 2{P_{\rm{e}}} + 1 $ | (14) |
而删除图案长度为N/(1-Pe),因此窃听者产生与编码器相同的删除图案的概率为
| $ {P_{\rm{w}}} = {\left( {{P_{\rm{s}}}} \right)^{\frac{N}{{1 - {P_{\rm{e}}}}}}} $ | (15) |
对于仿真时采用的Raptor码,N=19 000,若Pe=0.5,可得Pw=7.247 1×10-11 440.可见,窃听者产生与发送端一致的删除图案的概率几乎为0.
以上分析表明第1种破解方法几乎是不可能的.在第2种攻击中,密钥的保密性、长度和更新速度决定了方案的安全性能.基于无线信道特性生成密钥时,只要窃听者与合法接收者间的距离大于相干距离,两者获得的密钥就是相互独立的.采用保密信道共享密钥也能保证密钥的保密性.密钥的长度决定了窃听者破解的复杂度,密钥越长,破解的复杂度越高.因此,较大的密钥空间能保证密钥被破解的可能性很低.以仿真时采用的Mersenne Twister伪随机数发生器算法为例,该算法的种子长度为32位,这就意味着对窃听者而言,密钥空间为232≈4.295 0×109.目前基于无线信道特性生成密钥的生成速率已可达到10 bit/s[5],若伪随机数发生器算法的种子长度为32位,窃听者采用暴力破解密钥的方式,则要求其在3.2 s内从大小为4.295 0×109的密钥空间中找到正确的密钥.由于在每个密钥下都需要进行译码的尝试,在目前的计算机的计算能力下几乎是不可能的.同时,本文方案中有3个伪随机数发生器,窃听者任何一个的种子不对都不能产生正确的编码生成矩阵,实际上安全性是非常高的.
3 仿真结果对合法接收者和窃听者的误码性能进行仿真.仿真中,采用文献[6]中的Raptor码,外码为码率为0.95的规则(3, 60) LDPC码,内码为LT码,其度分布为式(13);输入符号长度为9 500,中间编码符号长度为10 000,发送的码字长度固定为19 000,总码率为0.5.译码时,LT码和LDPC码采用BP译码算法,最大迭代次数分别设定为100、50.每个信噪比下,合法接收者的误字数达到35后仿真停止.调制方式为二进制相移键控.伪随机数发生器采用Mersenne Twister算法,种子长度为32位.仿真了误比特率(BER, bit error rate)和误字率(WER, word error rate)随信噪比的变化情况. BER是接收错误比特数与总比特数之比. WER是接收错误码字数与总码字数之比.一个码字内任一比特出错该码字就出错,因此WER总是大于等于BER的.
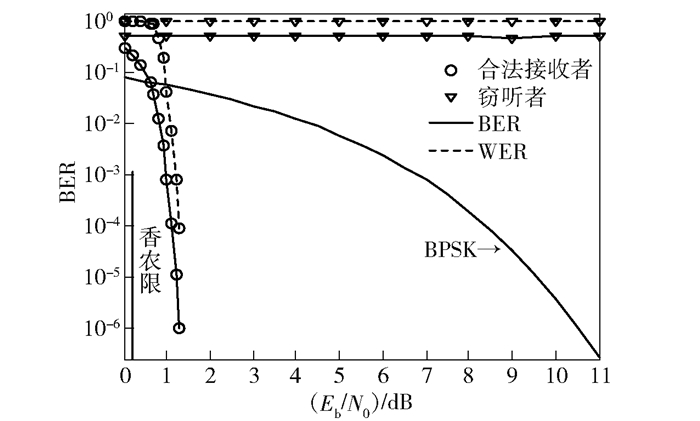
图 2所示为没有删除环节时AWGN信道下合法接收者和窃听者的误码性能的仿真结果,其中窃听者与合法接收者伪随机数发生器的种子仅有一个比特不同,不同比特的位置随机.图中“BPSK”表示AWGN信道下仅采用BPSK调制时的BER.仿真结果显示,在BER为10-5时,笔者所使用的Raptor码距离香农限仅差1.01 dB(码率为0.5时的香农限为0.19 dB),具有很好的纠错性能.对于窃听者,其差错性能不随信噪比的增加而改善,BER一直保持在0.5左右,而WER则始终为1.可见,在窃听者的种子与正确种子仅相差一位的情况下,窃听者仍保持非常高的错误概率,BER为0.5说明窃听者不能从接收到的信号中获得任何信息.
|
图 2 无随机删除时AWGN信道下的差错性能 |
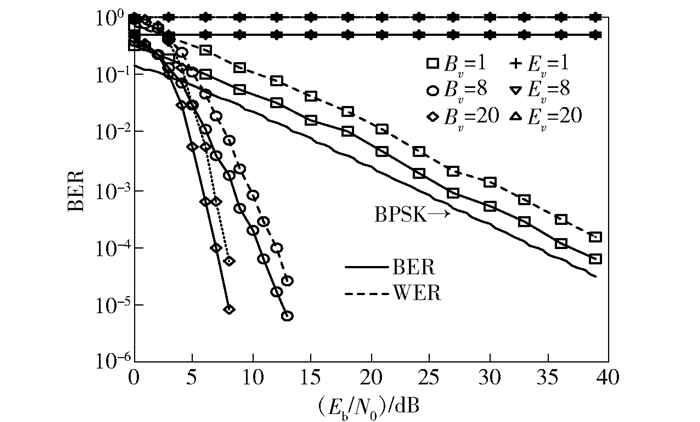
图 3所示为瑞利衰落信道下合法接收者和窃听者的差错性能仿真结果,种子产生方式与图 2仿真中的设置一致.合法信道与窃听信道都是平坦瑞利衰落信道,信道系数为独立同分布的复高斯随机变量,均值为0、方差为1.定义v为传输一个码字的时间内信道系数的变化次数,即每传输一个码字的1/v信道系数随机变化一次.仿真了v=1、8、20这3种情况下的性能.图中“BPSK”表示瑞利衰落信道下BPSK调制未编码时的BER.仿真结果显示,合法接收者瑞利衰落信道下的性能比AWGN信道差;而v值越大,误码性能越好,即信道系数变化越快,误码性能越好.这是因为一个码字内的码元是相互关联的,如果在一个码字的传输时间内信道发生变化,通过信道编码可实现时间分集.一个码字内信道变化的次数越多,获得的分集增益越大,译码后误码性能越好.窃听者的差错性能则与在AWGN信道下一样,BER保持在0.5左右,WER始终为1.
|
图 3 无随机删除时平坦瑞利衰落信道下的差错性能 |
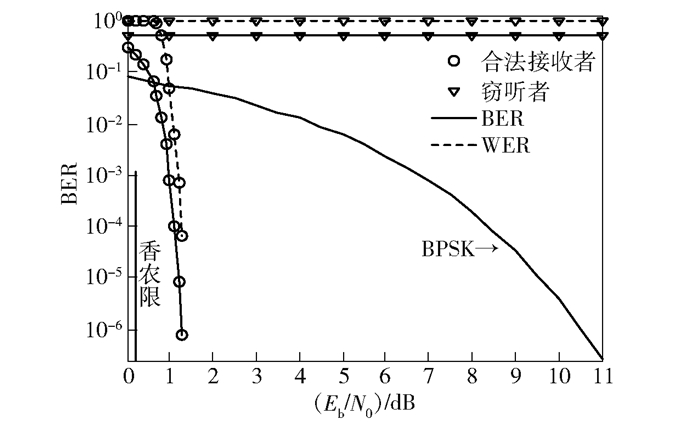
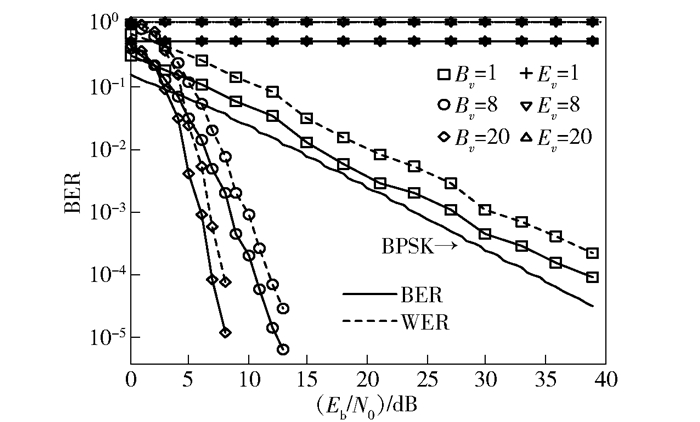
图 4、5所示为有随机删除时合法接收者和窃听者差错性能的仿真结果,图 4所示为AWGN信道下的仿真结果,图 5所示为瑞利衰落信道下3种不同信道衰落系数变化速度下的仿真结果.窃听者产生编码生成矩阵的伪随机数发生器的种子与编码器相同,但产生随机删除图案的伪随机数发生器的种子与编码器有一个比特不同,不同比特的位置随机. Pe为0.5.图中符号含义分别与图 2、3相同.将仿真结果与图 2、3对比可见,对合法接收者而言,增加随机删除后其差错性能没有变化,证明加入的随机删除环节并没有改变Raptor码的纠错性能.而对于窃听者,BER保持在0.5左右,WER始终为1.可见,窃听者即使能够获得与编码器相同的编码生成矩阵,但若不能获得正确的删除图案,也不能正常译码,不能从接收到的信号中获得任何信息.
|
图 4 有随机删除时AWGN信道下的差错性能 |
|
图 5 有随机删除时平坦瑞利衰落信道下的差错性能 |
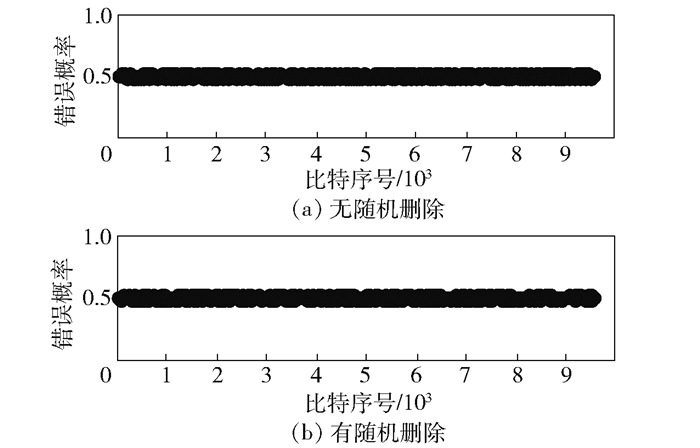
对于保密传输而言,窃听者的错误应为随机差错,各比特出错的概率应都为0.5,差错不应集中在码字某一部分,这样才能保证窃听者不能获得任何保密信息.为此还对窃听者译码后码字的每个信息位的错误概率进行了统计. 图 6所示为AWGN信道下、信噪比为1.3 dB时10 000个码字中同一个位置比特的平均错误率. 图 6(a)为没有随机删除环节、窃听者无正确编码生成矩阵伪随机数发生器种子时的结果,图 6(b)为有随机删除环节,窃听者能产生与编码器相同的编码生成矩阵,但产生随机删除图案的伪随机数发生器的种子不同时的结果,可见窃听者码字中每个信息比特的错误概率都在0.5左右.从信息论的角度来看,信道编码编码器的输入端到译码器的输出端可以看作一条二进制对称信道,窃听者接收比特的错误概率为0.5意味着消息经过了一个转移概率为0.5的二进制对称信道传输.而转移概率为0.5的二进制对称信道的信道容量为0,窃听者通过接收符号获得的关于发送符号的互信息为0,即窃听者从信道输出中不能获得任何信息.
|
图 6 窃听者码字各比特错误率分布 |
给出了一种基于无率纠错编码的保密方案,利用其优良的纠错性能,及编码中的随机性和译码中的互信息累积性,同时实现信息传输中的可靠性和安全性.本文方案在发送端和合法接收端设置伪随机数发生器,通过将密钥作为种子,同步产生编码生成矩阵,同时为增强安全性,还在编码器后增加了编码符号的随机删除.窃听者如果不能获得正确的密钥,即各伪随机数发生器的种子,就不能产生正确的编码生成矩阵,则即使在其已知编码的度分布、删除概率,以及伪随机数发生器的算法和结构下也无法正确译码.随机删除环节不改变编码符号的度分布,因此未改变编码的纠错能力.本文方案信息传输的安全性并不依赖于窃听信道与合法信道的质量差距,即使窃听信道质量远远优于合法信道,也能保证信息传输的安全.仿真结果表明,合法接收者的差错性能接近香农限,表明编码具有很好的纠错性能;而窃听者的BER保持为0.5,WER保持为1,其比特错误为随机差错,表明其不能从接收符号中获得任何信息.仿真证明了本文方案在实现信息可靠传输的同时,也实现了信息的保密传输.
| [1] |
Mceliece R J. A public-key cryptosystem based on algebraic coding theory[J]. Deep Space Network Progress Report, 1978, 44: 114-116. |
| [2] |
Sawant V, Bhise A. Cryptographic turbo code for image transmission over mobile networks[C]//International Conference on Advances in Computing, Communications and Informatics. Jaipur: IEEE, 2016: 844-850.
|
| [3] |
Ng T Y, Chew L Y, Puthusserypady S. Error correction with chaotic switching between convolutional codecs[J]. IEEE Transactions on Circuits & Systems, 2008, 55(11): 3655-3662. |
| [4] |
Esmaeili M, Gulliver T A. Joint channel coding-crypto-graphy based on random insertions and deletions in quasi-cyclic-low-density parity check codes[J]. IET Communications, 2015, 9(12): 1555-1560. DOI:10.1049/iet-com.2015.0026 |
| [5] |
Ye C, Mathur S, Reznik A, et al. Information-theoretically secret key generation for fading wireless channels[J]. IEEE Transactions on Information Forensics and Security, 2010, 5(2): 240-254. DOI:10.1109/TIFS.2010.2043187 |
| [6] |
Shokrollahi A. Raptor codes[J]. IEEE Transcations on Information Theory, 2006, 52(6): 2551-2567. DOI:10.1109/TIT.2006.874390 |



