2. 南京信息工程大学 江苏省大气环境与装备技术协同创新中心, 南京 210044;
3. 南京信息工程大学 计算机与软件学院, 南京 210044;
4. 鲁东大学 信息与电气工程学院, 烟台 264025
核四元数主成分分析(KQPCA)被成功应用于处理非线性四元数信号,然而,核矩阵维数太高使其对角化非常耗时,目前二维形式的KQPCA(2DKQPCA)并没有成功实现.对此,采用基于块处理和并行计算的思想,提出基于块的2DKQPCA(B2DKQPCA),实现真正意义上的2DKQPCA.基于时间复杂度、应用性能和分块矩阵应为四元数Hermitian矩阵的综合考虑,B2DKQPCA重点处理主对角线、反对角线和主对角线旁3个方向的小块.然后,结合B2DKQPCA与RGB-D图像四元数表示方法,将B2DKQPCA应用于RGB-D目标识别领域.在2个公开库上的实验结果表明,提出的基于列向B2DKQPCA的RGB-D识别算法优于现有基于主成分分析算法和基于卷积神经网络的一些算法.
2. Jiangsu Collaborative Innovation Center of Atmospheric Environment and Equipment Technology, Nanjing University of Information Science and Technology, Nanjing 210044, China;
3. School of Computer and Software, Nanjing University of Information Science and Technology, Nanjing 210044, China;
4. School of Information and Electrical Engineering, Ludong University, Yantai 264025, China
Currently, kernel quaternion principal component analysis (KQPCA) has been proposed and successfully applied to process linear quaternion signals. However, two dimensional version of KQPCA (2DKQPCA) has not been successfully implemented due to the quite time-consuming problem for diagonalizing the high dimensional kernel matrix. So, using the block-based idea and the parallel computing idea, the block-wise 2DKQPCA (B2DKQPCA) is proposed to implement 2DKQPCA really. After the overall consideration of computational complexity, application performance and quaternion Hermitian block, B2DKQPCA mainly processes the blocks of three directions:main-diagonal direction, anti-diagonal direction and side-diagonal direction. Then, B2DKQPCA is applied into RGB-D object recognition by combining B2DKQPCA and quaternion representation of RGB-D images. Experimental results on two publicly available datasets demonstrate that the proposed RGB-D object recognition algorithm based on the column direction B2DKQPCA outperforms some existing algorithms using principal component analysis and some existing algorithms using convolutional neural network.
在过去的20年中,彩色图像四元数表示方法(QR, quaternion representation)被广泛应用于处理彩色图像[1-11]:彩色图像的每个像素采用一个纯四元数来表示,3个通道作为它的3个虚部.其优势就是将彩色图像视为一个矢量整体并考虑了3个通道之间的内在联系[1-2, 10].但是,在采用四维四元数表示三维彩色图像时,其第4维会产生存储冗余和额外计算成本[12].为此,Chen等[7]将色彩信息与深度信息相结合,对该表示方法进行了改进,提出了一种基于四元数的RGB-D图像表征方法(RGBD_QR),并将RGBD_QR应用于RGB-D目标识别领域. RGBD_QR不仅额外考虑了在目标识别中具有重要作用的深度信息,而且将深度信息作为实部引入四元数中以避免存储冗余.因此,笔者也将继续采用RGBD_QR.
在模式识别、计算机视觉和多媒体信号处理中,主成分分析(PCA, principal component analysis)是一个非常重要的主要针对高维数据的特征提取技术.因此,一方面,基于传统的QR和四元数代数,Bihan[4]、郎方年[5]和Sun等[6]先后提出了四元数PCA(QPCA, quaternion PCA),将传统的PCA推广应用于彩色图像,随后Sun等[6]还提出了双向二维QPCA(BD2DQPCA, bidirectional two-dimensional QPCA);另一方面,为了有效地处理非线性情况,Schölkopf等[13]引入了核PCA(KPCA, kernel PCA). KPCA是PCA的非线性推广,它采用核技巧将输入数据映射到高维特征空间,从而将非线性问题转变为线性问题,然后在映射空间进行传统的PCA[13].
最近,Chen等[7]提出了主要用于处理非线性四元数信号的核QPCA(KQPCA, kernel QPCA),并且采用了RGBD_QR.但是,尽管Chen等[7]给出了二维KQPCA(2DKQPCA, two-dimensional KQPCA)的定义,但由于其核矩阵维数太高导致对角化对于普通计算机难以实现等原因,并没有实现真正的2DKQPCA,而是采用近似的思路:用平均行(或平均列)代表一幅图像.这实质上实现的是变相的一维KQPCA[7],破坏了图像的二维结构.因此,笔者将采用分块和并行计算的思路,提出基于块的2DKQPCA(B2DKQPCA, block-wise 2DKQPCA),尽可能地考虑图像的二维结构,实现真正的2DKQPCA,并结合B2DKQPCA与RGBD_QR应用于RGB-D的目标识别.
1 现有的2DKQPCA 1.1 四元数及RGBD_QR作为复数的推广,四元数在1843年由著名数学家Hamilton引入.一个四元数由一个实部和3个虚部构成:
| $ q = {q_r} + {q_i}{\rm{i}} + {q_j}{\rm{j}} + {q_k}{\rm{k}} $ | (1) |
其中:qr、qi、qj和qk∈R,i、j和k为3个满足如下运算规则的基本四元数单位.
| $ \begin{array}{*{20}{c}} {{{\rm{i}}^2} = {{\rm{j}}^2} = {{\rm{k}}^2} = - 1,{\rm{ij}} = - {\rm{ji}} = {\rm{k}},}\\ {{\rm{jk}} = - {\rm{kj}} = {\rm{i}},{\rm{ki}} = - {\rm{ik}} = {\rm{j}}} \end{array} $ |
如果式(1)中实部qr = 0,则称q为纯四元数.四元数q的模定义如下:
| $ \left| q \right| = \sqrt {{{\left( {{q_r}} \right)}^2} + {{\left( {{q_i}} \right)}^2} + {{\left( {{q_j}} \right)}^2} + {{\left( {{q_k}} \right)}^2}} $ | (2) |
为了解决现有彩色图像四元数表示方法存在的冗余问题,Chen等[7]提出新的RGBD_QR:通过引入对光照和色彩变化具有很强鲁棒性的深度信息作为四元数的实部分量,采用四元数表示RGB-D图像.令g(u, v)为1个RGB-D图像函数,其每个像素表示1个四元数:
| $ \begin{array}{*{20}{c}} {g(u,v) = {g_{\rm{D}}}(u,v) + {g_{\rm{R}}}(u,v){\rm{i}} + {g_{\rm{G}}}(u,v){\rm{j}} + }\\ {{g_{\rm{B}}}(u,v){\rm{k}}} \end{array} $ | (3) |
其中gD(u, v)、gR(u, v)、gG(u, v)和gB(u, v)分别为像素点(u, v)的深度、红色、绿色和蓝色分量.这里需要注意的是,在将深度信息和色彩信息整合前,深度信息的数值被归一化为[0, 255]. RGBD_QR至少在2个方面要优于传统的彩色图像四元数表示方法:①它不仅考虑了色彩信息而且同时考虑了在目标识别中具有重要作用的深度信息;②它将深度信息作为实部引入四元数中,避免了存储冗余.
1.2 2DKQPCA2DKQPCA既可从行向也可从列向进行.下面以文献[7]中定义的行向2DKQPCA为例,列向类似.行向2DKQPCA的主要思想就是先将四元数样本图像的行向量通过非线性映射函数映射到高维空间,然后再进行行向二维QPCA.由于不需要映射后样本的显示形式以及为了避免高维空间的高复杂度计算,Chen等[7]采用了核技术:用核矩阵代替映射后样本之间的协方差矩阵.
对大小为M×N的2D训练四元数数据样本图像Xs(s=1, 2, …, S),定义其四元数核矩阵K=(k(s-1)M+m, (t-1)M+n)SM×SM为
| $ \begin{array}{*{20}{c}} {{k_{(s - 1)M + m,(t - 1)M + n}} = k\left( {{\mathit{\boldsymbol{X}}_{s,m}},{\mathit{\boldsymbol{X}}_{t,n}}} \right),}\\ {1 \le s,t \le S,1 \le m,n \le M} \end{array} $ | (4) |
其中:Xs, m和Xt, n分别为第s个样本Xs的第m个行向量和第t个样本Xt的第n个行向量,k(Xs, m, Xt, n)是四元数形式的核函数.文献[7]中采用了如下所示的四元数多项式核函数:
| $ k\left( {{\mathit{\boldsymbol{X}}_{s,m}},{\mathit{\boldsymbol{X}}_{t,n}}} \right) = {\left( {{\mathit{\boldsymbol{X}}_{s,m}}{\mathit{\boldsymbol{X}}_{t,n}} + c} \right)^b} $ | (5) |
其中b和c为实数参数.
在求解四元数矩阵K的特征值之前,对K进行中心化:
| $ \mathit{\boldsymbol{\bar K}} = \mathit{\boldsymbol{K}} - {\mathit{\boldsymbol{E}}_{SM}}\mathit{\boldsymbol{K}} - \mathit{\boldsymbol{K}}{\mathit{\boldsymbol{E}}_{SM}} + {\mathit{\boldsymbol{E}}_{SM}}\mathit{\boldsymbol{K}}{\mathit{\boldsymbol{E}}_{SM}} $ | (6) |
其中ESM表示大小为SM×SM的所有元素值均为1/(SM)的矩阵.
由于K为四元数Hermitian矩阵,其特征值和特征向量的求解可以采用文献[5-6]中介绍的方法.限于篇幅,这里不再赘述.假设wt(t=1, 2, …, r)为K的最大r个特征值所对应的特征向量,则2DKQPCA投影矩阵为
| $ \mathit{\boldsymbol{W}} = \left[ {{\mathit{\boldsymbol{w}}_1},{\mathit{\boldsymbol{w}}_2}, \cdots ,{\mathit{\boldsymbol{w}}_r}} \right] $ | (7) |
对于一个新的样本X,其投影特征为
| $ \mathit{\boldsymbol{Y}} = {\mathit{\boldsymbol{W}}^{\rm{T}}}{{\mathit{\boldsymbol{\bar K}}}_X} = {\left( {{\mathit{\boldsymbol{Y}}_t}} \right)_{r \times 1}} = {\left( {\sum\limits_{\begin{array}{*{20}{c}} {1 \le s \le S}\\ {1 \le m \le M} \end{array}} {{w_{t,sM + m}}\bar k\left( {\mathit{\boldsymbol{X}},{\mathit{\boldsymbol{X}}_{s,m}}} \right)} } \right)_{r \times 1}} $ | (8) |
其中:wt, sM+m为特征向量wt的第(sM+m)个系数,KX为经式(6)中心化后的核矩阵,即
| $ {{\mathit{\boldsymbol{\bar K}}}_X} = {\left[ {\bar k\left( {\mathit{\boldsymbol{X}},{\mathit{\boldsymbol{X}}_{1,1}}} \right),\bar k\left( {\mathit{\boldsymbol{X}},{\mathit{\boldsymbol{X}}_{1,2}}} \right), \cdots ,\bar k\left( {\mathit{\boldsymbol{X}},{\mathit{\boldsymbol{X}}_{s,u}}} \right)} \right]^{\rm{T}}} $ | (9) |
其中:k(X, Xs, m)(s=1, 2, …, S; m=1, 2, …, M)为经式(6)中心化后的新样本X和所有SM个行向量训练样本Xs, m之间的四元数核系数,(·)T表示矩阵的转置运算.
2 B2DKQPCA事实上,2DKQPCA核矩阵的维数通常很高,尤其是当样本数量或者图像尺寸比较大时.比如,对于包括S个尺寸为M × N的二维四元数数据样本Xs的训练集,其行向和列向2DKQPCA核矩阵的维数分别为SM×SM和SN×SN.通常样本数量至少为1 000,图片尺寸至少为100×100,这样核矩阵维数至少为105×105.如此高维数的核矩阵为接下来的特征值求解带来非常大的计算量.因此,为了解决高计算复杂度的问题,Chen等[7]采用平均行或平均列代表一幅图像的近似思想,从而将核矩阵的维数减小为S×S,计算量大大减少,但是该思想严重破坏了图像的二维结构,并没有实现真正意义上的2DKQPCA.
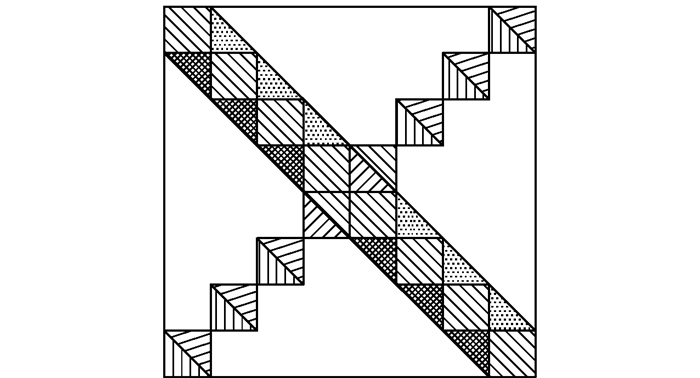
为了尽可能地考虑图像的二维结构,采用文献[14]针对二维KPCA(2DKPCA)的分块思想:首先对核矩阵划分为一些小块,然后对这些小块进行2DKPCA,最后将这些小块的投影特征整合作为原始核矩阵的投影特征.但是,如果考虑所有的分块,将带来2个方面的问题:一方面,尽管分块思想使得每块的计算更简单,但大数量的分块导致时间复杂度还是很大;另一方面,由于核矩阵本身为四元数Hermitian(或称自共轭)矩阵,所以除了主对角小块为四元数Hermitian矩阵外,其他分块都不是.但是,目前四元数矩阵的特征求解方法主要针对四元数Hermitian矩阵.因此,基于时间复杂度、应用性能和分块矩阵应为四元数Hermitian矩阵的综合考虑,如图 1所示,满足自共轭性质的小块包括所有主对角线方向的小块(纹理为右下方向斜线)、由主对角线旁方向的三角区域(纹理为方格和散点)构造出的四元数Hermitian矩阵小块以及由反对角线方向的小块(纹理为竖线和左下方向斜线)构造出的四元数Hermitian矩阵小块.对于主对角线方向的小块,已是四元数Hermitian矩阵,因此直接处理即可.对于主对角线旁方向,以图 1左上角第1个下三角块(纹理为散点)和上三角块(纹理为方格)为例,将上三角块和下三角块沿对角线进行拼接得到四元数Hermitian矩阵小块,以此类推,可得主对角线旁方向的所有四元数Hermitian矩阵小块.对于反对角线方向,以一对小块(右上角的第1个小块和左下角的最后1个小块)为例,将右上角小块中斜线纹理的上三角部分(竖线纹理的下三角部分)与左下角小块中竖线纹理的下三角部分(斜线纹理的上三角部分)进行拼接得到四元数Hermitian矩阵小块,以此类推,可得反对角线方向的所有四元数Hermitian矩阵小块.
|
图 1 考虑图像块的示意图 |
图 1所示3个方向(主对角线、反对角线和主对角线旁)的小块进行2DKQPCA是可以完全独立的,因此为了进一步提升计算效率,考虑采用并行处理的思想.根据本课题组的计算机配置情况,采用单个CPU3个核并行计算,每个核处理一个方向上的所有小块.本课题计算机配置为ThinkStation P500,CPU为E5-2620v3,内存为16 GB.
3 B2DKQPCA在RGB-D目标识别中的应用作为PCA的一种改进算法,B2DKQPCA可以主要应用于包括人脸识别、虹膜识别和目标识别在内的模式识别领域,这些应用按照识别目标的数量可分为单目标识别和多目标识别.对于多目标识别,通常需要先进行多目标分割,随后对各个目标进行识别.也就是说,不管是单目标识别还是多目标识别,都需要对单个目标进行识别.因此,本节将详细介绍B2DKQPCA在RGB-D单目标识别中的应用,提出一种基于B2DKQPCA的RGB-D单目标识别算法.在其他识别方面的应用可以参照该算法.
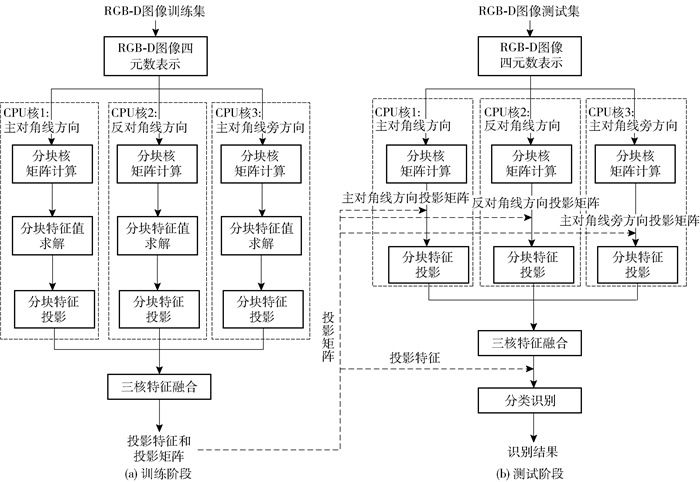
2DKQPCA可以用于处理四维四元数信号.而且,如前文所述,传统的QR在使用四维四元数表示只拥有3个分量的彩色图像时会导致存储冗余及额外计算负担.因此,采用Chen等[7]提出的如式(3)所示的RGBD_QR,并将其与B2DKQPCA相结合,提出一种新的RGB-D目标识别算法,该算法的流程如图 2所示.训练阶段和测试阶段的具体步骤如下所述(注意,这里是以行向2DKQPCA为例,列向2DKQPCA与之类似).
|
图 2 提出的基于B2DKQPCA的RGB-D目标识别算法流程 |
1) 训练阶段
① RGB-D图像四元数表示.首先采用式(3)所示的RGBD_QR将S个尺寸为M×N的RGB-D训练样本Xs(s=1, 2, …, S)表示为四元数矩阵Xs,然后视Xs的每一行Xs, m (m=1, 2, …, M)为新的训练样本.
② 分核分块核矩阵计算.由图 1所示,不考虑所有的小块,因此只需计算所考虑小块的核矩阵.而且,不同方向的小块采用不同CPU核并行计算.假设分块大小为L×L,对于第n个小块中的某个元素(x, y),1≤x, y≤L,1≤n≤[SM/L],[·]表示取整,通过式(4)计算kx, y=k(Xs′, nL+x+M-s′M, Xs′, nL+x+M-s′M),这里s′=
③ 分核分块求解投影矩阵.对②中获得的3个方向的所有核矩阵块按方向分核处理,首先通过式(6)对其进行中心化,然后对中心化后的所有核矩阵块求解特征值和特征向量,取最大r个特征值所对应的特征向量,进而由式(7)得到2DKQPCA投影矩阵Wdir,dir∈{dir1, dir2, dir3}.
④ 分核分块特征投影.基于③中获得的3个方向上的投影矩阵Wdir,分核分别通过式(8)对每个小块所对应的训练样本Xs, m进行投影,得到3个方向的投影特征Ys, mdir={YsM+m, hdir|h=1, 2, …, r},dir∈{dir1, dir2, dir3},s=1, 2, …, S,m =1, 2, …, M.
⑤ 三核特征整合.将3个核分别获取的投影特征进行整合.比如,对训练样本Xs,其M行3个方向整合在一起的特征为Ys={Ys, 1dir1, Ys, 2dir1, …, Ys, Mdir1, Ys, 1dir2, …, Ys, Mdir3}.然后,将所有训练样本的投影特征Ys (s=1, 2, …, S)整合作为整个训练集的特征.
2) 测试阶段
① RGB-D图像四元数表示.首先采用式(3)所示的RGBD_QR将T个尺寸为M×N的RGB-D测试样本Zt(t=1, 2, …, T)表示为四元数矩阵Zt,然后视Zt的每一行Zt, m (m=1, 2, …, M)为新的测试样本.
② 分核分块核矩阵计算.由于需要采用训练阶段获取的投影矩阵对测试样本进行投影,因此这里所分小块的行数必须与训练阶段小块的行数一致,即也为L.与训练阶段一样,对于不同方向采用不同的CPU核.假设分块大小为L×P,对于第n个小块中的某个元素(x, y),1≤x≤L, 1≤y≤P,1≤n≤[SM/L],则可以通过式(4)计算
③ 分核分块特征投影.对②中获得的所有核矩阵块按方向分核处理,首先对核矩阵
| $ \mathit{\boldsymbol{\overline K}} _n^{{\rm{dir}}} = \mathit{\boldsymbol{\tilde K}}_n^{{\rm{dir}}} - {\mathit{\boldsymbol{E}}_L}\mathit{\boldsymbol{\tilde K}}_n^{{\rm{dir}}} - \mathit{\boldsymbol{\tilde K}}_n^{{\rm{dir}}}{\mathit{\boldsymbol{E}}_P} + {\mathit{\boldsymbol{E}}_L}\mathit{\boldsymbol{\tilde K}}_n^{{\rm{dir}}}{\mathit{\boldsymbol{E}}_P} $ | (10) |
其中:EL是大小为L×L所有元素均为1/L的矩阵,EP是大小为P×P所有元素均为1/P的矩阵;然后采用训练阶段获取的投影矩阵Wdir,dir∈{dir1, dir2, dir3},通过式(8)对每个小块所对应的测试样本Zt, m进行投影,得到3个方向的投影特征
④ 三核特征整合.将3个核获取的特征进行整合.比如,对测试样本Zt,其M行3个方向整合在一起的特征为
⑤ 分类识别.基于④中获取的测试集特征以及训练阶段获取的训练集特征,采用基于四元数欧氏距离的最邻近分类器进行分类识别.这里需要强调的是,为了更好地测试KQPCA投影特征的性能,采用简单的最邻近分类器.这里也可以采用其他分类器,如支持向量机、神经网络、贝叶斯等.
众所周知,特征距离是最邻近分类器的关键.以测试样本Zt为例,为了确定Zt所在的类,计算Zt与所有训练样本Xs (s=1, 2, …, S)之间的四元数欧氏距离:
| $ \begin{array}{*{20}{c}} {{d_{t,s}} = {{\left\| {{{\mathit{\boldsymbol{\tilde Y}}}_t} - {\mathit{\boldsymbol{Y}}_s}} \right\|}_2} = }\\ {\sqrt {\sum\limits_{{\rm{dir}} \in \left\{ {{\rm{dir1}},{\rm{dir2,dir3}}} \right\}} {\sum\limits_{m = 1}^M {\sum\limits_{h = 1}^r {{{\left| {\mathit{\boldsymbol{\tilde Y}}_{\iota M + m,h}^{{\rm{dir}}} - \mathit{\boldsymbol{Y}}_{sM + m,h}^{{\rm{dir}}}} \right|}^2}} } } } } \end{array} $ | (11) |
其中:║·║2表示文献[6]中定义的四元数向量欧氏距离,|·|则为式(2)所示的四元数模运算.
然后采用最邻近分类器进行识别.如果s*=
下面将通过RGB-D目标识别实验来测试提出的B2DKQPCA的性能.为了更好地展示算法的性能,提出算法与现有一些基于PCA的算法(基于四元数的BD2DQPCA[6]及BD2DKQPCA[7]、传统的基于块的2DKPCA(B2DKPCA, block-wise 2DKPCA)[15])进行了对比. BD2DQPCA在文献[6]中应用于彩色人脸识别,在这里结合如式(3)所示的RGBD_QR进行RGB-D目标识别. B2DKPCA在文献[15]中用于灰度人脸识别,在这里将B2DKPCA先独立处理RGB-D目标图像的每个分量,然后进行整合,从而实现RGB-D目标识别.
为了便于实验对比,采用与文献[7]相同的实验数据(相同的训练和测试样本).实验数据为2个分别针对人脸和一般物体的公开RGB-D数据库:ⅢT-D库[16]和CIN 2D/3D库[17].对于IIIT-D库:①包括了106个个体的总共4 065幅RGB-D人脸图像,每个个体的图像数从11~254不等;②它的人脸图像是在正常光照条件下具有姿势、表情和眼镜遮盖等变化;③包括5个文件夹,每个文件夹可以单独进行一次实验[16],即每个个体的4幅图像用于训练,其他图像用于测试;④类似于文献[16],所有图像的尺寸归一化为100×100.
对于CIN 2D/3D库:①它包括18个类别的163个个体;②对于每个个体,它包括36个不同视角的RGB-D图像,相邻2个视角相差10°;③实验中只考虑了每个类的前2个个体,而且没有考虑一些尺寸特别小(如5×5)的图像,对于每个个体,随机选择14幅不同视角的图像进行训练,剩余的22幅图像进行测试;④所有图像的尺寸也归一化为100×100.算法涉及的一些参数设置:式(5)定义的多项式核函数中的实数b和c分别取为1和1.5,IIIT-D库尺寸为42 400×42 400的核矩阵的分块大小为424×424,CIN 2D/3D库尺寸为50 400×50 400的核矩阵的分块大小为504×504.
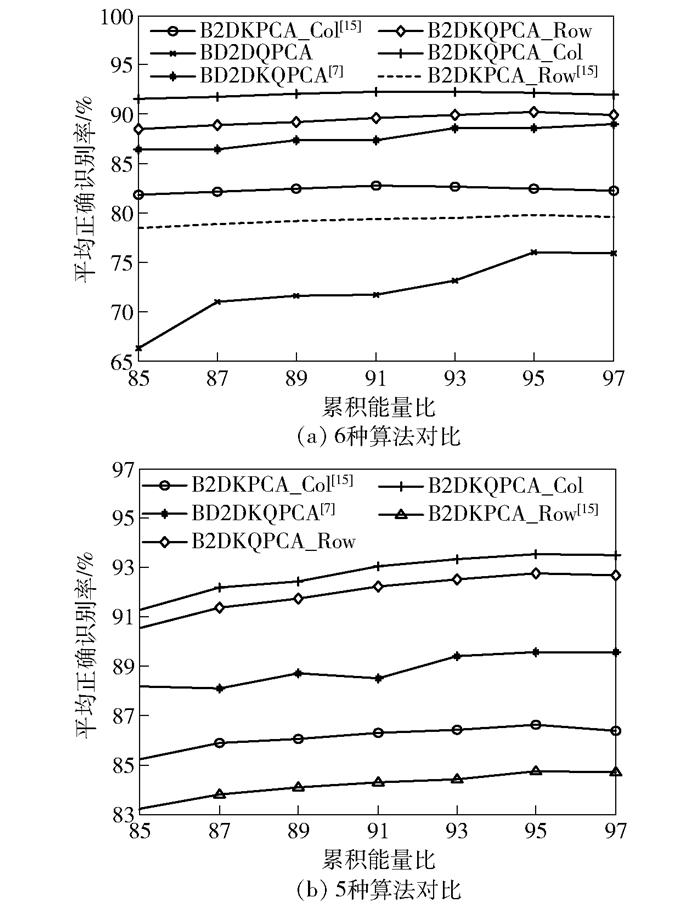
图 3(a)给出各算法在这2个不同数据库上的平均识别率,其中B2DKPCA[15]和提出的B2DKQPCA都具有行向和列向2种算法:B2DKPCA_Row[15]和B2DKPCA_Col[15]、B2DKQPCA_Row和B2DKQPCA_Col. 图 3(b)是为了更好地展示其中的5种算法随累积能量比变化的趋势.由图 3可以看出:①各算法的识别率一开始均随累积能量比的增大而提高,但当累积能量比达到95%时,识别率趋于稳定,这是因为图像特征之间通常是存在冗余的;②对于任意的累积能量比,提出的B2DKQPCA_Col算法优于其余对比算法,这主要归因于基于四元数的处理思想、非线性核方法以及图像二维结构的考虑等因素;③对于B2DKPCA[15]和提出的B2DKQPCA,列向算法均优于行向算法,这与文献[7]中取平均列算法优于取平均行算法的结果一致.由图 3可知,当累积能量比达到95%时,算法趋于稳定.因此,接下来上述一些基于PCA的算法采用最优累积能量比95%的结果与其余算法进行对比.同时,为了测试深度信息的有效性,还与修改的提出算法2DKQPCA_RGB_Row和2DKQPCA_R-GB_Col进行了对比,这2种修改算法只考虑色彩信息而不考虑深度信息.
|
图 3 各算法在不同累积能量比下的平均正确识别率 |
针对2个数据库的结果分别如表 1和表 2所示. 表 1同时提供了由IIIT-D数据库创建者提出的2个算法(RISE和RISE+ADM)[16]的结果;表 2则同时给出了针对CIN 2D/3D库的现有5种算法(Ev2D3D[17]、CNN-TRANSFER+DAE[18]、CNN-SPM-RNN[19]、Upgraded HMP[20]和Multi-Modal CNN[21])的结果,这些结果均来源于相应文献.由表 1和表 2可以看出:①提出的B2DKQPCA_Col算法在所有对比算法中效果最优,优于一些基于卷积神经网络(CNN, convolutional neural networks)的算法[18-19, 21]以及最近提出的同样基于KQPCA的BD2DKQPCA算法[7];②考虑深度信息较不考虑深度信息正确识别率能提高1%左右.为了进一步分析深度信息对目标识别的有效性,并且2个数据库中深度图像的质量不高,因此通过对深度图像添加不同程度的高斯噪声,然后采用提出的B2DKQPCA_Col算法进行识别,从而测试深度图像质量对识别的影响.
|
|
表 1 各算法针对IIIT-D库的正确识别率 |
|
|
表 2 各算法针对CIN 2D/3D库的正确识别率 |
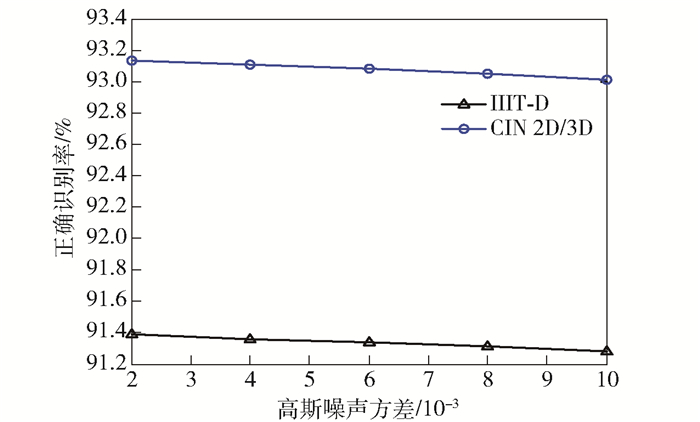
图 4展示了提出算法在IIIT-D库和CIN 2D/3D库上的结果.可知,随着噪声强度不断增强,识别率不断降低,深度图像质量对识别具有一定的影响,但影响不大.
|
图 4 B2DKQPCA_Col算法在不同程度噪声下的正确识别率 |
笔者采用分块和并行计算的思想,提出了B2DKQPCA,实现了真正的2DKQPCA.同时,在QR中引入深度信息解决现有QR存在的存储冗余和额外计算开销问题,进而提出了结合B2DKQPCA与RGBD_QR的RGB-D目标识别算法.实验表明,提出的基于B2DKQPCA_Col的RGB-D目标识别算法优于现有的一些算法:①优于一些非基于四元数的算法[15-21],这主要归功于提出算法考虑了RGB-D图像4个分量的整体性;②优于一些非核方法[6, 16-21],这主要是因为提出算法适用于处理高度非线性的现实场景中RGB-D目标识别问题[14, 22];③优于最近提出的基于BD2DKQPCA的算法[7],这主要是因为提出算法充分考虑了图像的二维空间信息;④优于不考虑深度信息只考虑色彩信息的B2DKQPCA_RGB_Row和B2DKQPCA_RGB_Col算法,这主要归功于深度信息在识别中的有效性.
| [1] |
Subakan O N, Vemuri B C. A quaternion framework for color image smoothing and segmentation[J]. International Journal of Computer Vision, 2011, 91(3): 233-250. DOI:10.1007/s11263-010-0388-9 |
| [2] |
Ell T A, Sangwine S J. Hypercomplex Fourier transforms of color images[J]. IEEE Transactions on Image Processing, 2007, 16(1): 22-35. |
| [3] |
Gai S. New banknote defect detection algorithm using quaternion wavelet transform[J]. Neurocomputing, 2016, 196: 133-139. DOI:10.1016/j.neucom.2015.12.112 |
| [4] |
Bihan N L, Sangwine S J. Quaternion principal component analysis of color images[C]//2003 10th IEEE International Conference on Image Processing (ICIP 2003). Barcelona: [s.n.], 2003: 809-812. http://www.researchgate.net/publication/221126690_Quaternion_principal_component_analysis_of_color_images
|
| [5] |
郎方年, 周激流, 闫斌, 等. 四元数矩阵正交特征向量系的求解方法及其在彩色人脸识别中的应用[J]. 自动化学报, 2008, 34(2): 121-129. Lang Fangnian, Zhou Jiliu, Yan Bin, et al. Obtain method of quaternion matrix orthogonal eigenvector set and its application in color face recognition[J]. Acta Automatica Sinica, 2008, 34(2): 121-129. DOI:10.3969/j.issn.1003-8930.2008.02.022 |
| [6] |
Sun Y F, Chen S Y, Yin B C. Color face recognition based on quaternion matrix representation[J]. Pattern Recognition Letters, 2011, 32(4): 597-605. DOI:10.1016/j.patrec.2010.11.004 |
| [7] |
Chen B J, Yang J H, Jeon B, et al. Kernel quaternion principal component analysis and its application in RGB-D object recognition[J]. Neurocomputing, 2017(266): 293-303. |
| [8] |
Saoud L S, Ghorbani R, Rahmoume F. Cognitive quaternion valued neural network and some applications[J]. Neurocomputing, 2017(221): 85-93. |
| [9] |
王金伟, 周春飞, 王水平, 等. 基于分数阶四元数傅里叶变换的彩色图像自适应水印算法[J]. 电子与信息学报, 2016, 38(11): 2832-2839. Wang Jingwei, Zhou Chunfei, Wang Shuiping, et al. Color image adaptive watermarking algorithm using fractional quaternion Fourier transform[J]. Journal of Electronics and Information Technology, 2016, 38(11): 2832-2839. |
| [10] |
Yang H Y, Liang L L, Li Y W, et al. Quaternion exponent moments and their invariants for color image[J]. Fundamenta Informaticae, 2016, 145(2): 189-205. DOI:10.3233/FI-2016-1354 |
| [11] |
Chen B J, Qi X M, Sun X M, et al. Quaternion pseudo-Zernike moments combining both of RGB information and depth information for color image splicing detection[J]. Journal of Visual Communication and Image Representation, 2017(49): 283-290. |
| [12] |
Assefa D, Mansinha L, Tiampo K F, et al. The trinion Fourier transform of color images[J]. Signal Processing, 2011, 91(8): 1887-1900. DOI:10.1016/j.sigpro.2011.02.011 |
| [13] |
Schölkopf B, Smola A, Muller K R. Nonlinear component analysis as a kernel eigenvalue problem[J]. Neural Computation, 1998, 10(5): 1299-1319. DOI:10.1162/089976698300017467 |
| [14] |
Eftekhari A, Forouzanfar M, Moghaddam H A, et al. Block-wise 2D kernel PCA/LDA for face recognition[J]. Information Processing Letters, 2010, 110(17): 761-766. DOI:10.1016/j.ipl.2010.06.006 |
| [15] |
Sun N, Wang H X, Ji Z H, et al. An efficient algo-rithm for kernel two-dimensional principal component analysis[J]. Neural Computing Applications, 2008, 17(1): 59-64. |
| [16] |
Goswami G, Vatsa M, Singh R. RGB-D face recognition with texture and attribute features[J]. IEEE Transactions on Information Forensic and Security, 2014, 9(10): 1629-1640. DOI:10.1109/TIFS.2014.2343913 |
| [17] |
Browatzki B, Fischer J, Graf B, et al. Going into depth: evaluating 2D and 3D cues for object classification on a new, large-scale object dataset[C]//2011 IEEE International Conference on Computer Vision Workshops (ICCV2011). Barcelona: [s.n.], 2011: 1189-1195. http://www.researchgate.net/publication/221429888_Going_into_depth_Evaluating_2D_and_3D_cues_for_object_classification_on_a_new_large-scale_object_dataset
|
| [18] |
Tang J H, Jin L, Li Z C, et al. RGB-D object recognition via incorporating latent data structure and prior knowledge[J]. IEEE Transactions on Multimedia, 2015, 17(11): 1899-1908. DOI:10.1109/TMM.2015.2476660 |
| [19] |
Cheng Y, Zhao X, Huang K, et al. Semi-supervised learning and feature evaluation for RGB-D object recognition[J]. Computer Vision and Image Understanding, 2015, 139: 149-160. DOI:10.1016/j.cviu.2015.05.007 |
| [20] |
Bo L F, Ren X F, Fox D. Unsupervised feature learning for RGB-D based object recognition[C]//13th International Symposium on Experimental Robotics. Québec City: [s.n.], 2013: 387-402. http://link.springer.com/10.1007/978-3-319-00065-7_27
|
| [21] |
Wang A R, Lu J W, Cai J F, et al. Large-margin multi-modal deep learning for RGB-D object recognition[J]. IEEE Transactions on Multimedia, 2015, 17(11): 1887-1898. DOI:10.1109/TMM.2015.2476655 |
| [22] |
Zhang H, Parker L E. CoDe4D:color-depth local spatio-temporal features for human activity recognition from RGB-D videos[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2016, 26(3): 541-555. DOI:10.1109/TCSVT.2014.2376139 |


