2. 北京邮电大学 天地互联与融合北京市重点实验室, 北京 100876
针对不同轨道角动量(OAM)叠加的涡旋光束探测问题,提出了基于机器学习的模式识别技术,为OAM叠加光束的检测提供了一个新思路.基于修正的von Karman功率谱模型,利用功率谱反演法生成随机相位屏,应用多步衍射法数值模拟拉盖尔高斯叠加光束在大气湍流信道的传输.研究了不同波长、传输距离和大气湍流信道条件下训练的卷积神经网络(CNN)分别对各种湍流强度测试集的识别正确率.结果表明:对于较弱的湍流、波长较长的OAM光束和较短的传输距离条件,基于CNN的OAM模式识别正确率较高;对于各种湍流条件的测试数据,使用强湍流训练集训练得到的模型与使用弱湍流训练集训练得到的模型相比识别正确率更高;利用混合训练集进行训练有利于提高识别正确率.这些结果对OAM光束解复用系统的实现具有一定的参考价值.
2. Beijing Key Laboratory of Space-Ground Interconnection and Convergence, Beijing University of Posts and Telecommunications, Beijing 100876, China
In order to solve the problem of detection of different orbital angular momentum (OAM) superimposed vortex beams, a pattern recognition technology based on machine learning (ML) is proposed, which provides a brand-new method for multi-OAM states detection. In order to study the recognition rate of multi-OAM beams using convolutional neural network (CNN) models under different wavelength, transmission distance and atmospheric turbulence conditions, the numerical simulation phase screens are generated by the power spectral inversion method based on the modified von Karman power spectrum model. Multi-step diffraction method is used to simulate numerically the propagation of OAM beams in the atmospheric turbulence, and the training and testing database are obtained under different atmospheric turbulence. Results indicate the accuracy of CNN-based OAM pattern recognition increases as wavelength increases, transmission distance decreases and turbulent intensity decreases. And the CNN trained with the database under strong turbulence has high accuracy for all kind of turbulence condition, and using mixed training database under different turbulence condition can enhance the accuracy. These results contribute to the demultiplexing systems of free space optical-OAM systems.
1992年,Allen等[1]指出具有相位项exp (ilφ)的涡旋光束每光子具有lħ的轨道角动量(OAM,orbital angular momentum),其中ħ=h/2π,h为普朗克常数,拓扑荷l可以取任意整数,l也被称作角向指数,ϕ为方位角.由于携带不同OAM模式的光束是相互正交的,将OAM光束进行复用传输将极大地提升光通信系统的容量和频带利用率,所以OAM通信近年得到了研究者的广泛关注[2-3].
在系统的接收端,将复用的OAM光束进行解复用是一个关键技术.常见的共轭相位掩模检测法是将拓扑荷为l的涡旋光束加载拓扑荷为-l的螺旋相位,通过观察接收平面是否有OAM态l=0的亮斑来进行探测和识别,该方法每次只能识别一个OAM态,若识别多个态则需要将接收光束分束,能量效率较低[4].基于坐标变换的OAM分离方案将不同OAM模式的光束转换成倾斜角不同的截断平面波,然后通过透镜将其聚焦到探测平面上不同的位置,从而实现OAM光束的分离[5],该方案能量利用率高,由于相邻模式光斑之间有重叠导致模式串扰较大.利用上述方法进行解复用是基于OAM光束的相位信息,自由空间光(FSO,free space optical)OAM通信系统对大气湍流、横向偏移、角向倾斜等十分敏感,并对光路的对准要求非常高[6],往往需要昂贵的自适应光学校正系统.
最近,机器学习方法被广泛应用于图像识别和光通信等领域. 2014年,Krenn等[7]首次提出利用BP-ANN模型识别叠加拉盖尔高斯(LG,Laguerre-Gaussian)光束的强度图,采用了16种组合,其错误率约为1.7%. 2016年,Knutson[8]等利用VGG16模型对110个不同的OAM态进行分类,其分类正确率为74%. 2017年,Doster和Watnik[9]提出利用Alexnet模型对贝塞尔高斯复用光束进行识别,其解复用效果要优于传统方法. 2017年,Li等[10]对比研究了BP-ANN、KNN、NBC和卷积神经网络(CNN,convolutional neural network)机器学习方法对LG复用光束解复用的识别率,结果表明CNN要优于其他方法.这些工作表明,基于机器学习的模式识别为OAM叠加光束的检测提供了一个崭新的思路.
笔者研究利用CNN对经过大气湍流信道传输的复用光束进行识别和解复用.首先,理论分析了LG叠加光束的横向光强分布特点;然后,研究了使用不同湍流、波长以及传输距离条件下的训练集训练的CNN分别对各种湍流强度的测试集的识别正确率变化.
1 基于卷积神经网络的FSO-OAM系统模型 1.1 仿真系统结构图图 1为多OAM态FSO-OAM通信系统结构.系统主要由激光器、空间光调制器(SLM,spatial light modulator)、CCD相机等组成.在发射端,激光器发射出的高斯光束经过SLM的调制得到叠加的OAM光束. OAM光束经过大气湍流信道时,湍流会对其螺旋相位造成扭曲,接收端利用CCD相机接收叠加光束的强度图,并利用基于CNN的解复用器识别叠加OAM态,恢复原始信息.

|
图 1 多OAM态FSO-OAM通信仿真系统结构 |
LG光束是一种最常见的携带OAM的涡旋光束,径向指数p=0的LG光束其复振幅在柱坐标系(r, ϕ, z)中可表示为[1]
| $ \begin{array}{*{20}{l}} {\begin{array}{*{20}{c}} {{U_l}(r,\phi ,z) = }\\ {\sqrt {\frac{2}{{{\rm{\pi }}|l|!}}\frac{1}{{w(z)}}{{\left[ {\frac{{r\sqrt 2 }}{{w(z)}}} \right]}^{1/1}}\exp \left[ {\frac{{ - {r^2}}}{{{w^2}(z)}}} \right]\exp ({\rm{i}}l\phi ) \times } } \end{array}}\\ {\exp \left[ {\frac{{{\rm{i}}k{r^2}z}}{{2\left( {{z^2} + z_{\rm{R}}^2} \right)}}} \right]\exp \left[ { - {\rm{i}}(|l| + 1)\arctan \left( {\frac{z}{{{z_{\rm{R}}}}}} \right)} \right]} \end{array} $ | (1) |
其中:r为径向距离;l为方位角指数,取整数;w(z)=w0
OAM模值为-l和l的光束叠加生成的波包不随传输距离变化而旋转[11],可形成相对稳定的光斑图样,且具有便于产生和探测的特点.在任意一个垂直于光轴并以光轴为圆心的圆环上(r, z为常数),设LG光束U-l(r, θ, z)和μUl(r, θ, z)对应的复振幅分别为A1eiθ1和A2eiθ2,μ为强度相对分布的正实数,叠加后的复振幅可表示为
| $ E(r,\phi ,z) = {A_1}{{\rm{e}}^{{\rm{i}}{\theta _1}}}\exp ( - {\rm{i}}l\phi ) + {A_2}{{\rm{e}}^{{\rm{i}}{\theta _2}}}_{{\rm{exp}}}({\rm{i}}l\phi ) $ | (2) |
叠加光束的强度分布为
| $ \begin{array}{l} I = {\left| {E(r,\phi ,z)} \right|^2} = \\ A_1^2 + A_2^2 + 2{A_1}{A_2}\cos \left( {2l\phi + {\theta _2} - {\theta _1}} \right) \end{array} $ | (3) |
式(3)表明,叠加光束的横向光强呈周期性分布,形成了|2l|个“花瓣”形的光斑强度图样.由式(3)经分析可得,当A1=A2,即μ=1时I可取0值,此时叠加光束的“花瓣”间出现了零值点,更有利于提高图样的空间分辨能力.为了描述光斑强度分布的紧凑程度,引入如下锐利度函数:
| $ {S = \frac{{\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {I_{i,j}^2} } }}{{{{\left( {\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{I_{i,j}}} } } \right)}^2}}}} $ | (4) |
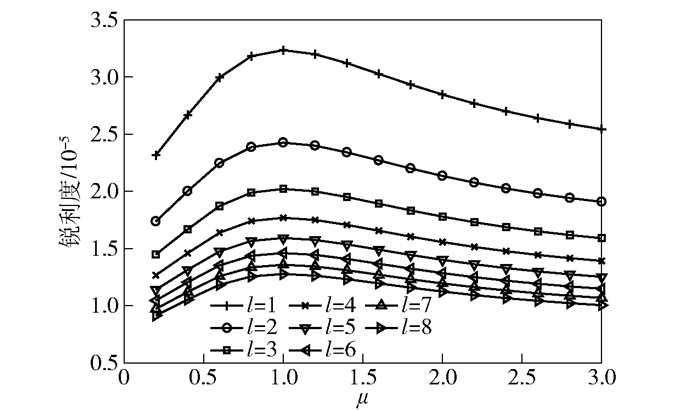
其中:Ii, j为光强I离散化后像素点(i, j)的光强值,N为光强的纵向和横向像素点的个数. 图 2给出了z=1 km, w0=1 cm, λ=1 550 nm, μ=1(上)和μ=0.2(下),±l, (l=1, 2, 3, 4, 5, 6, 7, 8)光束叠加后的光斑图样. 图 3为μ取不同值时叠加光束光斑图样的锐利度曲线.

|
图 2 ±l的LG光束叠加后的光强分布 |
|
图 3 μ取不同值时±l叠加光束光斑图样的锐利度曲线 |
由图 2可见,μ=1的光斑图样与μ=0.2的相比显得更清晰,这与图 3给出的锐利度描述是一致的.所以,选用OAM模值为±l(l=1, 2, 3, 4, 5, 6, 7, 8)的等强度光作为8种复用类别.
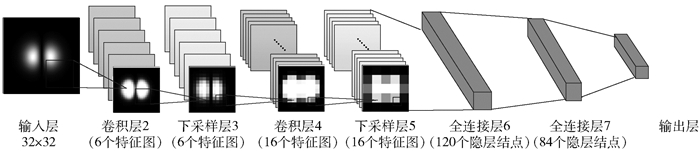
1.3 卷积神经网络解复用器CNN是一种多层监督学习网络,能够逐层提取原始图像的特征,最终获得特征的非线性表达,其相对于传统的神经网络避免了复杂的特征提取设计和数据重建过程[12].本文采用CNN模型作为多OAM态解复用器来识别经大气湍流信道传输后的光束强度图,其示意图如图 4所示.该模型包含8层.第1层为输入层.第2层为卷积层,其由6个特征图组成,每个特征图是采用5×5的卷积核与输入图像做卷积得到的,不同特征图卷积核参数不同,从而提取不同的特征.第3层为下采样层,使用大小为2×2的采样窗口进行最大池化操作,其能减小特征图的尺寸,降低特征维数,同时在一定程度上增加网络对位移、缩放和扭曲的鲁棒性.同理,第4层为卷积层,其由16个特征图组成,采用5×5的卷积核.第5层的操作与第3层相同.这样,第5层的输出可以作为输入图像的不同特征输入到带有激活函数的第6层(全连接层),最后经带有激活函数的第7层(全连接层)输出得到图像的OAM模式信息(第8层,即输出层),其中激活函数为tanh函数.
|
图 4 基于CNN的多OAM态解复用器示意图 |
光束在空间信道传输会受到大气湍流效应的影响,从而导致相位畸变.利用功率谱反演法产生随机相位屏来模拟大气湍流效应具有实现简单、计算精度高的特点,适用于不同形式的大气湍流模型[13].采用修正的von Karman功率谱模型,利用功率谱反演法构造大气湍流随机相位屏,用多步衍射法来数值模拟光束在大气湍流信道的传输[14].
仿真中参数设置如下:大气湍流内尺度和外尺度分别取l0=0.000 2 m,L0=50 m,束腰半径w0=1 cm,光束图像的横向和纵向像素点数N=1 024,随机相位屏间距Δz=100 m. CNN参数设置如下:学习率为0.1,每批次训练数为50.考虑到计算机硬件条件和计算速度,将输入神经网络的图片像素数调整为32×32.
2.2 仿真结果和讨论研究了在不同大气湍流、波长、传输距离以及数据集条件下,基于CNN的OAM模式识别正确率.
图 5为当波长λ取1 550 nm,传输距离z为1 km时,不同大气湍流条件下,±l态叠加的LG光束强度分布图(l=1, 2, 3, 4, 5, 6, 7, 8),图 5中大气折射率结构参数Cn2分别取10-16 m-2/3、10-15 m-2/3和10-14 m-2/3.从图 5可以看出,随着Cn2的增加,接收得到的光斑强度分布弥散得越严重.当Cn2取定值时,每一种类别分别收集1 000张图片作为训练集,100张图片作为测试集.

|
图 5 不同大气湍流强度下接收到的±l态叠加的LG光束强度分布 |
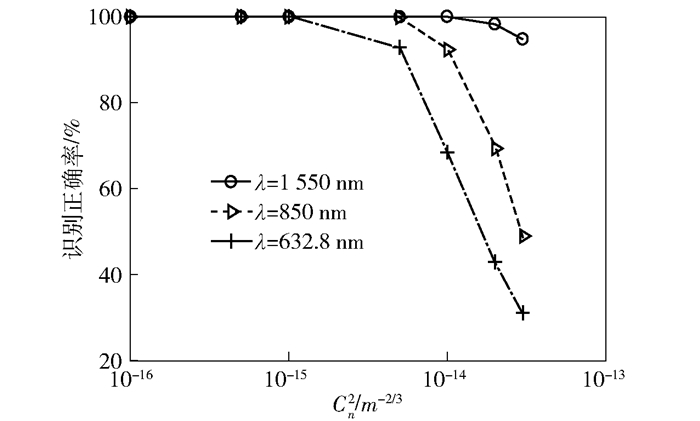
图 6为当传输距离z为1 km时,不同波长条件下,基于CNN的OAM模式识别正确率随Cn2的变化曲线.从图 6中可以看出,OAM模式识别正确率随着Cn2的增加而降低.并且,当Cn2取值小于1×10-15 m-2/3时,不同波长下的OAM模式识别正确率都为100%;当Cn2取值大于1×10-15 m-2/3时,长波长光束的OAM模式识别正确率明显要大于短波长光束.结果表明,基于CNN的OAM模式识别方法对长波长光束的识别拥有更高的识别正确率.
|
图 6 不同波长条件下,基于CNN的OAM模式识别正确率随Cn2的变化曲线 |
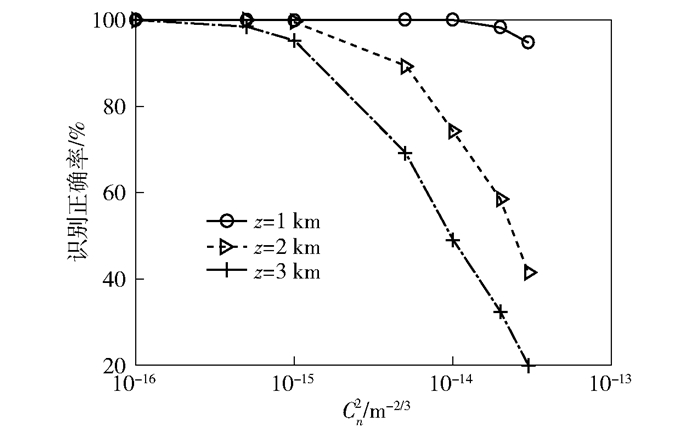
图 7为当波长λ取1 550 nm时,不同传输距离条件下,基于CNN的OAM模式识别正确率随Cn2的变化曲线.从图 7中可以看出,当Cn2值给定时,OAM模式识别正确率随着距离的增加而下降.另外,当Cn2取值较大时,即大气湍流强度变强时,距离z=1 km的OAM模式识别正确率大于90%,表明基于CNN的OAM模式识别方法适用于短距离中弱湍流条件.
|
图 7 不同传输距离下,基于CNN的OAM模式识别正确率随Cn2的变化曲线 |
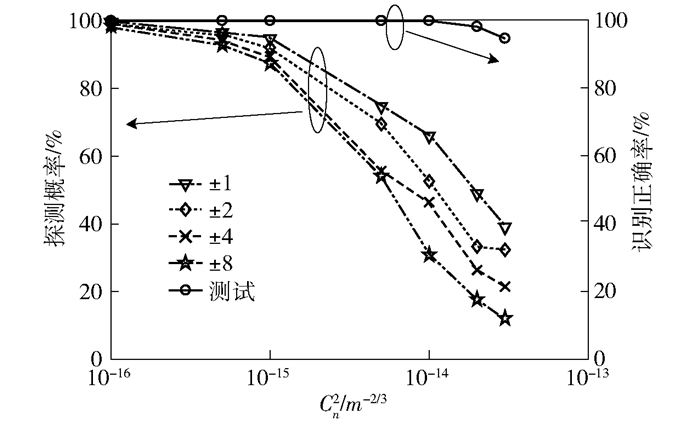
为了与传统的基于共轭相位掩模检测法进行比较,图 8同时给出了当波长λ取1 550 nm,传输距离z为1 km,不同OAM复用态时,基于CNN的OAM模式识别正确率和基于共轭相位掩模检测法的OAM模式探测概率随Cn2的变化曲线[6].从图中可以看出,随着Cn2值的增加,OAM模式探测概率曲线逐渐下降,湍流带来的畸变越来越严重.然而,利用CNN进行解复用时,当Cn2小于1×10-14 m-2/3时,OAM模式识别正确率均为100%.当Cn2从1×10-14 m-2/3增加到3×10-14 m-2/3时,CNN的识别正确率缓慢下降到94.37%.通过比较2种方法得到的结果可以看出,CNN的模式识别正确率要明显高于共轭相位掩模检测法的探测概率,尤其是在强湍流情况下.并且基于CNN的OAM模式识别方法对系统的严格对准、OAM模式严格正交等要求降低[9].但是,对于湍流较强的情况,基于CNN的OAM模式识别方法的模型训练时间较长,可以利用特定的硬件来减少计算开销[9].
|
图 8 不同大气湍流强度下OAM模式识别正确率和探测概率 |
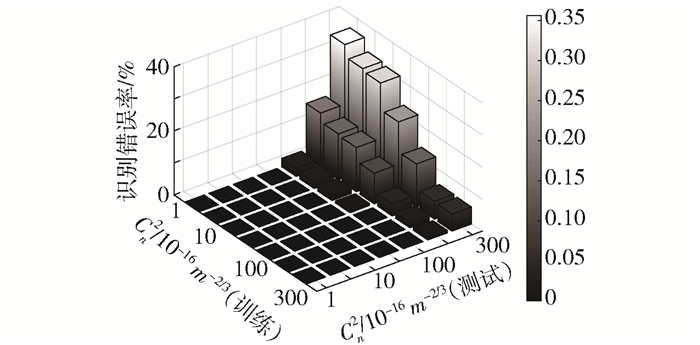
为了研究训练集的选取对识别正确率的影响,利用某一湍流条件下的训练集进行训练,测试不同湍流条件下OAM模式的识别正确率. 图 9为当波长λ取1 550 nm,传输距离z为1 km时,不同湍流强度的训练集和测试集组合对应的OAM模式识别错误率.从图 9可以看出,利用弱湍流训练集得到的模型进行测试时,可以得到较好的识别效果,随着湍流的加强,错误率增长较快,1×10-16 m-2/3训练集/3×10-14 m-2/3测试集组合的错误率约为0.356 2;利用强湍流训练集得到的模型进行测试时,相对可以得到更好的识别正确率,这是因为大气湍流强度越大,接收得到的OAM强度图之间的随机变化也越大,使得训练集更具多样性,训练得到的模型具有更高的识别正确率.
|
图 9 基于CNN的OAM识别错误率 |
下面讨论混合数据集及其大小对识别正确率的影响. 表 1给出了当波长λ取1 550 nm,传输距离z为1 km时,2个混合数据集的识别正确率.其中混合数据集1为从7种Cn2训练集中各选取1 000张图片组成训练集,从7种Cn2测试集中各选取120张图片构成各自的新测试集;混合数据集2为将7种训练集数据全部混合在一起(共5.6万张图片)构成训练集,原测试集不变.从表 1可以看出,使用混合数据集2训练得到的模型的识别正确率更高,说明增大数据集可以提高识别正确率;与单一训练集相比,混合训练集得到的模型的识别正确率更高.
|
|
表 1 混合数据集及其大小对OAM模式识别正确率的影响 |
研究了不同大气湍流条件下CNN对OAM叠加光束的识别正确率.结果表明,对于波长较长的OAM光束,较短的传输距离和较弱的湍流条件下,基于CNN的OAM模式识别正确率较高.对于各种湍流条件下的测试数据,使用强湍流训练集训练得到的模型与使用弱湍流训练集训练得到的模型相比识别正确率更高;利用混合训练集进行训练有利于提高识别正确率.
| [1] |
Allen L, Beijersbergen M W, Spreeuw R J, et al. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes[J]. Physical Review A, 1992, 45(11): 8185-8189. DOI:10.1103/PhysRevA.45.8185 |
| [2] |
Wang Jian, Yang J Y, Fazal I M, et al. Terabit free-space data transmission employing orbital angular momentum multiplexing[J]. Nature Photonics, 2012, 6(7): 488-496. DOI:10.1038/nphoton.2012.138 |
| [3] |
Ren Yongxiong, Wang Zhe, Liao Peicheng, et al. Experimental characterization of a 400 Gbit/s orbital angular momentum multiplexed free-space optical link over 120 m[J]. Optics Letters, 2016, 41(3): 622-625. DOI:10.1364/OL.41.000622 |
| [4] |
Khonina S N, Kotlyar V V, Skidanov R V, et al. Gauss-Laguerre modes with different indices in prescribed diffraction orders of a diffractive phase element[J]. Optics Communications, 2000, 175(4-6): 301-308. DOI:10.1016/S0030-4018(00)00472-7 |
| [5] |
Berkhout G C, Lavery M P, Courtial J, et al. Efficient sorting of orbital angular momentum states of light[J]. Physical Review Letters, 2010, 105(15): 153601. DOI:10.1103/PhysRevLett.105.153601 |
| [6] |
Yin Xiaoli, Sang Hongqing, Cui Xiaozhou, et al. Offset tolerance of an orbital angular momentum optical communication system with angular deflection[J]. Optics Communications, 2017(393): 34-39. |
| [7] |
Krenn M, Fickler R, Fink M, et al. Communication with spatially modulated light through turbulent air across Vienna[J]. New Journal of Physics, 2014(16): 113028. |
| [8] |
Knutson E M, Lohani S, Danaci O, et al. Deep learning as a tool to distinguish between high orbital angular momentum optical modes[C]//Optics and Photonics for Information Processing X. Bellingham: SPIE, 2016: 997013. http://www.researchgate.net/publication/308122970_Deep_learning_as_a_tool_to_distinguish_between_high_orbital_angular_momentum_optical_modes?ev=auth_pub
|
| [9] |
Doster T, Watnik A T. Machine learning approach to OAM beam demultiplexing via convolutional neural networks[J]. Applied Optics, 2017, 56(12): 3386-3396. DOI:10.1364/AO.56.003386 |
| [10] |
Li Jin, Zhang Min, Wang Danshi. Adaptive demodulator using machine learning for orbital angular momentum shift keying[J]. IEEE Photonics Technology Letters, 2017, 1-1. |
| [11] |
苏明样.面向光通信的光学涡旋传输特性及复用技术研究[D].深圳: 深圳大学, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10590-1017812436.htm
|
| [12] |
芮挺, 费建超, 周遊, 等. 基于深度卷积神经网络的行人检测[J]. 计算机工程与应用, 2016, 52(13): 162-166. Rui Ting, Fei Jianchao, Zhou You. Pedestrian detection based on deep convolutional neural network[J]. Computer Engineering and Applications, 2016, 52(13): 162-166. DOI:10.3778/j.issn.1002-8331.1502-0122 |
| [13] |
Fu Shiyao, Gao Chunqing. Influences of atmospheric turbulence effects on the orbital angular momentum spectra of vortex beams[J]. Photonics Research, 2016, 4(5): B1. DOI:10.1364/PRJ.4.0000B1 |
| [14] |
Andrews L C, Phillips R L. Laser beam propagation through random media[M]. 2nd ed. Bellingham: SPIE PRESS, 2005: 57-80.
|


