2. 国家电网有限公司 全球能源互联网研究院, 北京 102209
针对复杂电磁脉冲噪声环境下的空闲信道检测难题,提出一种基于贝叶斯统计推理框架的新检测算法.为了应对脉冲干扰并提升检测精度,建立了一种全新的动态状态空间模型,采用伯努利随机有限集来描述脉冲噪声与信道状态的动态变化特性.在此基础上,基于序贯估计与粒子滤波理论,设计出一种新型信道检测机制.在检测信道状态的同时,对脉冲噪声出现时间和幅值进行联合估计,有效消除了其对信道检测的干扰;同时,通过发掘脉冲噪声的动态特性,显著提升了信道检测性能,为复杂电磁环境下的高可靠信道检测提供了一种新的解决方案.数值仿真验证了所提算法的有效性.
2. Global Energy Interconnection Research Institute, State Grid Corporation of China, Beijing 102209, China
Aiming at the idle channel detection problem under impulsive noise environments, a new detection scheme is proposed based on Bayesian statistical reasoning framework. To cope with impulsive interference and improve probability of detection, a novel dynamic state-space model is established, in which the dynamic variations of impulsive noise and channel status are described by Bernoulli random finite sets. On the basis of above, a novel channel detection mechanism is designed based on sequential estimation and particle filtering theory. At the same time of detecting channel status, the proposed scheme jointly estimates the occurrence and amplitude of impulsive noise, therefore eliminating its interference on channel detection. Moreover, the channel detection performance can be significantly improved based on utilizing the dynamic property of impulsive noise, thus providing a promising solution for channel detection with high reliability under complex electromagnetic environments. Numerical simulations verify the effectiveness of the proposed algorithm.
智能电网(SG,smart grid)将先进无线通信技术与自动化控制技术融合至电力传输过程,为复杂电磁环境下的变电设备实时监管和异常处理提供了一种革新性的实现方案,能极大限度提升其监管与应对的效率,并确保无线变电站的安全正常运转.为确保监测与异常信息的及时上报,通常需借助于无线信道检测技术,以及时发现空闲信道发送紧急数据.在复杂无线电磁环境中,高可靠的无线空闲信道检测机制将变得尤为重要.
然而复杂无线电磁环境对智能电网中包括空闲信道检测在内的无线通信技术也提出了难题.具体而言,复杂无线电磁场景中的噪声/干扰除了常见的热噪声之外,还与变电设备的运转(譬如瞬时变化的开关效应)密切相关.以脉冲噪声/干扰为例,其在时域中呈现出一定稀疏性,而幅值/能量却通常远超于有用信号.上述复杂脉冲干扰电磁环境无疑对传统无线通信信号处理技术带来巨大的挑战[1].
主流的信道检测方法包括能量检测(ED,energy detection)与载波侦听(CS,carrier sense)[2].相比之下,能量检测方法无需任何先验信息,且具备实现简单的优势,因而已在无线通信设计中得到了广泛应用.如前所述,对于面向变电站应用的复杂无线电磁环境而言,信道检测过程中可能出现持续时间很短、且幅值很高的脉冲噪声,致使能量观测量呈现出显著的随机波动,其统计特性不确定性进一步导致信道检测性能的严重下降.
为了应对无线电磁脉冲噪声/干扰对可靠信道检测的影响,创新性地提出了一种基于贝叶斯统计推理理论框架的新型信道检测方案.显著区别于传统的二元假设检验模型,新方案通过建立动态状态空间模型充分发掘利用信道占用状态和脉冲噪声的动态时变特性以及相互耦合关系,将脉冲噪声下的信道检测问题抽象为一个联合检测与估计问题,在执行高精度信道检测的同时,对脉冲噪声的出现时间与幅值进行联合估计.为无线变电站环境中灵活高效的信息传输提供了一种极具应用潜力的方案.
1 系统信号模型针对脉冲噪声下的空闲信道检测问题,提出一种新型动态状态空间模型描述系统各状态,并针对信道状态、脉冲噪声以及能量观测值分别建模.
1.1 动态状态空间模型为更好描述系统状态动态特性,建立动态状态空间模型[3]如下:
| $ \left. \begin{array}{l} {S_{{x_{k,m}}}} = F\left( {{S_{{x_{k - 1,m}}}}} \right),\\ {I_{{i_{k,m}}}} = H\left( {{I_{{i_{1 \cdots k - 1,m}}}}} \right),\;\;\;k = 1,2, \cdots ,K,m = 1,2, \cdots ,M\\ {y_k} = O\left( {{x_{k,m}},{i_{k,m}},{w_{k,m}}} \right), \end{array} \right\} $ | (1) |
其中,前两方程为状态方程,后一方程为观测方程. k为离散检测时隙序号;m为检测时隙内离散采样点序号,M检测周期内采样点数目. S表示检测时隙的信道占用状态,其状态变化由状态转移函数F(·)描述;xk, m表示k时隙采样点m处的信号幅值. I表示检测时隙脉冲噪声状态,其状态变化由状态转移函数H(·)描述;ik, m表示k时隙m采样点处的脉冲噪声幅值. yk为k时隙的能量观测值,由观测方程O(·)描述;wk, m为信道背景噪声.
1.2 信道占用状态待检测信道有2种可能状态:以S0表示空闲;S1表示占用.进一步将信道占用状态用一个两状态一阶马尔可夫过程来描述,即当前检测时隙信道状态只与前一检测时隙有关[4],状态转移概率矩阵为
| $ \mathit{\boldsymbol{ \boldsymbol{\varPi} }} = \left[ {\begin{array}{*{20}{c}} {1 - {p_b}}&{{p_b}}\\ {1 - {p_s}}&{{p_s}} \end{array}} \right] $ | (2) |
其中:pb表示前一检测时隙待检测信道为空闲状态而当前时刻被占用的概率;ps表示在前一检测时隙待检测信道被占用而当前时刻信道仍被占用的概率,即
| $ \left. {\begin{array}{*{20}{l}} {{p_b} = Pr\left\{ {{S_k} = {S_1}|{S_{k - 1}} = {S_0}} \right\}}\\ {{p_s} = Pr\left\{ {{S_k} = {S_1}|{S_{k - 1}} = {S_1}} \right\}} \end{array}} \right\} $ | (3) |
当前检测时隙信道中脉冲噪声有2种可能状态:以I0表示不存在;I1表示存在.设脉冲噪声的出现间隔离散时隙服从参数为1/λ泊松分布.基于此,脉冲噪声在检测时隙层面上可用一阶马尔可夫过程描述,其当前时隙概率分布可由上一个脉冲噪声出现时隙预测.定义pI为基于上一个脉冲噪声出现时隙k′预测时隙k的出现概率,即
| $ {p_I} = Pr\left\{ {{I_k} = {I_1}|{I_{{k^\prime }}} = {I_1}} \right\} $ | (4) |
在此基础上,假设脉冲噪声的幅值服从均值为i,方差为σi2的高斯分布.
需注意,为不失一般性,对脉冲噪声出现间隔和幅值的假设可扩展至任意形式的概率分布.
1.4 能量信号观测模型采用接收到的信号在特定时间窗内的能量累积值作为系统观测值,可继承传统能量检测方法实现简单、复杂度低的优点[5].对于能量观测值yk,由于在每一检测时隙内,观测到的能量值可分为信道状态是否为空闲以及是否存在脉冲噪声的4种情况,故能量观测方程为
| $ {y_k} = \left\{ {\begin{array}{*{20}{l}} {\sum\limits_{m = 1}^M {w_{k,m}^2} ,{S_k} = {S_0},{I_k} = {I_0}}\\ {\sum\limits_{m = 1}^M {{{\left( {{i_{k,m}} + {w_{k,m}}} \right)}^2}} ,{S_k} = {S_0},{I_k} = {I_1}}\\ {\sum\limits_{m = 1}^M {{{\left( {{x_{k,m}} + {w_{k,m}}} \right)}^2}} ,{S_k} = {S_1},{I_k} = {I_0}}\\ {\sum\limits_{m = 1}^M {{{\left( {{x_{k,m}} + {i_{k,m}} + {w_{k,m}}} \right)}^2}} ,{S_k} = {S_1},{I_k} = {I_1}} \end{array}} \right. $ | (5) |
其中信道背景噪声/热噪声wk, m建模为零均值高斯随机变量,方差为σ2,即wk, m~$\mathscr{N}$(0, σ2),且独立于信道占用信号以及脉冲噪声.
2 联合估计信道检测算法基于上述系统信号模型,提出一种基于贝叶斯序贯推理框架与伯努利随机有限集合(BRFS,Bernoulli random finite set)的新型空闲信道联合检测算法.具体而言,首先以序贯形式在每检测时刻获取前时刻信道状态与脉冲噪声的后验概率分布估计结果,并基于先验信息与历史信息预测上述两系统状态BRFS的先验概率分布;进一步基于预测概率分布与能量观测值计算联合后验形式的似然函数;进而利用似然函数对预测概率分布进行更新,推导信道状态与脉冲噪声BRFS的后验概率分布;最后,依据所制定判决准则对系统状态后验概率分布进行判决.所提算法的实施进一步采用基于蒙特卡洛思想的粒子滤波(PF,particle filtering)理论降低运算与实现复杂度.
2.1 伯努利随机有限集合考虑到信道占用状态与脉冲噪声的占用/存在情况未知,且占用/存在情况下幅值仍为随机变量,利用伯努利随机有限集合描述上述两系统状态,即信道占用状态$\mathscr{S}$和脉冲噪声$\mathscr{I}$.其含义在于将系统状态表示为基数服从伯努利分布的集合,当取单元素集合时该元素也为随机变量[6].
对于检测时隙k的信道占用状态$\mathscr{S}$k,设信道被占用的概率为q,信号幅值空间概率分布为t(xk).信道占用状态$\mathscr{S}$k的概率分布为
| $ f\left( {{\mathscr{S}_k}} \right) = \left\{ {\begin{array}{*{20}{l}} {1 - q,}&{{\mathscr{S}_k} = \emptyset }\\ {qt\left( {{x_k}} \right),}&{{\mathscr{S}_k} = \left\{ {{x_k}} \right\}} \end{array}} \right. $ | (6) |
令函数ϕ为$\mathscr{S}$k的状态转移函数,分时隙k-1信道状态的2种可能情况分别讨论,基于式(6)有
| $ {\phi _{k|k - 1}}\left( {{\mathscr{S}_k}|\emptyset } \right) = \left\{ {\begin{array}{*{20}{l}} {1 - {p_b},}&{{\mathscr{S}_k} = \emptyset }\\ {{p_b}\beta \left( {{x_k}} \right),}&{{\mathscr{S}_k} = \left\{ {{x_k}} \right\}}\\ {0,}&{\left| {{\mathscr{S}_k}} \right| \ge 2} \end{array}} \right. $ | (7) |
| $ {\phi _{k|k - 1}}\left( {{\mathscr{S}_k}|\left\{ {{x_{k - 1}}} \right\}} \right) = \left\{ {\begin{array}{*{20}{l}} {1 - {p_s},}&{{\mathscr{S}_k} = \emptyset }\\ {{p_s}\beta \left( {{x_k}} \right),}&{{\mathscr{S}_k} = \left\{ {{x_k}} \right\}}\\ {0,}&{\left| {{\mathscr{S}_k}} \right| \ge 2} \end{array}} \right. $ | (8) |
其中β(xk)为占用信号幅值xk的概率分布.
设脉冲噪声$\mathscr{I}$k出现的概率为p,幅值空间概率分布为r(ik).则脉冲噪声$\mathscr{I}$k的概率分布为
| $ f\left( {{\mathscr{T}_k}} \right) = \left\{ {\begin{array}{*{20}{l}} {1 - p,}&{{\mathscr{T}_k} = \emptyset }\\ {pr\left( {{i_k}} \right),}&{{\mathscr{T}_k} = \left\{ {{i_k}} \right\}} \end{array}} \right. $ | (9) |
由于k时隙脉冲噪声概率分布只与前一次脉冲噪声出现的检测时隙k′有关,令函数ζ为脉冲噪声$\mathscr{I}$k的状态转移函数,表示为
| $ {\zeta _{k|{k^\prime }}}\left( {{\mathscr{T}_k}|\left\{ {{i_{{k^\prime }}}} \right\}} \right) = \left\{ {\begin{array}{*{20}{l}} {1 - {p_I},}&{{\mathscr{T}_k} = \emptyset }\\ {{p_l}{\mu _k}\left( {{i_k}} \right),}&{{\mathscr{T}_k} = \left\{ {{i_k}} \right\}}\\ {0,}&{\left| {{\mathscr{T}_k}} \right| \ge 2} \end{array}} \right. $ | (10) |
其中μk(ik)为时隙k脉冲噪声幅值空间概率分布.对于出现概率pI,基于上述脉冲噪声间隔统计分布推导得时隙k脉冲噪声出现概率为
| $ {p_I} = \frac{{\frac{{{\lambda ^{k - {k^\prime }}}}}{{\left( {k - {k^\prime }} \right)!}}{{\rm{e}}^{ - \lambda }}}}{{\frac{{{\lambda ^{k - {k^\prime }}}}}{{\left( {k - {k^\prime }} \right)!}}{{\rm{e}}^{ - \lambda }} + \sum\limits_{j = 1}^\infty {\frac{{{\lambda ^{k + j - {k^\prime }}}}}{{\left( {k + j - {k^\prime }} \right)!}}{{\rm{e}}^{ - \lambda }}} }} $ | (11) |
通过以上的分析可以得出,对于两系统状态的序贯联合估计等价于对于$\mathscr{S}$k的后验概率qk|k与对于$\mathscr{I}$k的后验概率pk|k以及噪声存在情况下的后验空间概率rk|k(ik)的序贯估计.
2.2 系统状态预测基于贝叶斯统计推理框架,根据先验及历史信息,对信道状态与脉冲噪声概率分布进行预估计,称为先验概率分布.
对于信道状态,设k-1时隙$\mathscr{S}$k-1的后验概率分布为fk-1|k-1($\mathscr{S}$k-1|y1:k-1),并考虑信道状态转移函数ϕ,根据Chapman-Kolmogorov方程推导$\mathscr{S}$k的先验概率分布为
| $ \begin{array}{*{20}{c}} {{f_{k|k - 1}}\left( {{\mathscr{S}_k}|{y_{1;k - 1}}} \right) = }\\ {\int {{\phi _{k|k - 1}}} \left( {{\mathscr{S}_k}|{\mathscr{S}_{k - 1}}} \right){f_{k - 1|k - 1}}\left( {{\mathscr{S}_{k - 1}}|{y_{1;k - 1}}} \right)\delta {\mathscr{S}_{k - 1}}} \end{array} $ | (12) |
进一步根据伯努利随机有限集合定义推导$\mathscr{S}$k先验概率分布为[5]
| $ \left. {\begin{array}{*{20}{l}} {{q_{k|k - 1}} = {p_b}\left( {1 - {q_{k - 1|k - 1}}} \right) + {p_s}{q_{k - 1|k - 1}}}\\ {{t_{k|k - 1}}\left( {{x_k}} \right) = \frac{{{p_b}\left( {1 - {q_{k - 1|k - 1}}} \right)\beta \left( {{x_k}} \right)}}{{{q_{k|k - 1}}}} + \frac{{{p_s}{q_{k - 1|k - 1}}\beta \left( {{x_k}} \right)}}{{{q_{k|k - 1}}}}} \end{array}} \right\} $ | (13) |
对于脉冲噪声,设k′时隙后验概率分布为fk′|k′($\mathscr{I}$k'|y1:k′),根据Chapman-Kolmogorov方程推导得$\mathscr{I}$k的先验概率分布为
| $ \begin{array}{*{20}{c}} {{f_{k|{k^\prime }}}\left( {{\mathscr{T}_k}|{y_{1:{k^\prime }}}} \right) = }\\ {\int {{\zeta _{k|{k^\prime }}}} \left( {{\mathscr{T}_k}|{\mathscr{T}_{{k^\prime }}}} \right){f_{{k^\prime }|{k^\prime }}}\left( {{\mathscr{T}_{{k^\prime }}}|{y_{1:{k^\prime }}}} \right)\delta {\mathscr{T}_{{k^\prime }}}} \end{array} $ | (14) |
则进一步推导$\mathscr{I}$k先验概率分布结果为
| $ \left. {\begin{array}{*{20}{l}} {{p_{k|{k^\prime }}} = {p_I}}\\ {{r_{k|{k^\prime }}}\left( {{i_k}} \right) = {\mu _k}\left( {{i_k}} \right)} \end{array}} \right\} $ | (15) |
信道占用状态与脉冲噪声在系统能量观测值中的相互耦合关系,将严重影响信道检测性能.因此,设计了一种边缘化似然函数计算方法,以分析描述两系统状态间的嵌套耦合关系.
对于能量观测值似然函数有:1) $\mathscr{S}$k=Ø,$\mathscr{I}$k=Ø时,能量观测值yk服从自由度为M的中心卡方分布;2) $\mathscr{S}$k={xk},$\mathscr{I}$k=Ø时,能量观测值yk服从自由度为M的非中心卡方分布;3) $\mathscr{I}$k={ik}时,能量观测值yk均服从自由度为M+1的广义卡方分布,为方便计算以非中心卡方分布近似令函数g(yk|$\mathscr{S}$k, $\mathscr{I}$k)表示对应各信道状态及脉冲噪声状态的似然函数,有[7]
| $ \left. {\begin{array}{*{20}{l}} {g\left( {{y_k}|{\mathscr{S}_k} = \emptyset ,{\mathscr{T}_k} = \emptyset } \right) = \chi _M^2\left( {{y_k};0} \right)}\\ {g\left( {{y_k}|{\mathscr{S}_k} = \emptyset ,{\mathscr{T}_k} = \left\{ {{i_k}} \right\}} \right) \approx \chi _{M + 1}^2\left( {{y_k};{\kappa _1}} \right)}\\ {g\left( {{y_k}|{\mathscr{S}_k} = \left\{ {{x_k}} \right\},{\mathscr{T}_k} = \emptyset } \right) = \chi _M^2\left( {{y_k};{\kappa _2}} \right)}\\ {g\left( {{y_k}|{\mathscr{S}_k} = \left\{ {{x_k}} \right\},{\mathscr{T}_k} = \left\{ {{i_k}} \right\}} \right) \approx \chi _{M + 1}^2\left( {{y_k};{\kappa _3}} \right)} \end{array}} \right\} $ | (16) |
其中κ1、κ2、κ3为非中心参数.
进一步地,在$\mathscr{S}$k、$\mathscr{I}$k各自的似然函数过程中,考虑将先验概率分布作为先验信息,提出以边缘化概率期望思想推导两系统状态后验形式似然函数.具体来说,计算$\mathscr{S}$k似然函数φk(yk|$\mathscr{S}$k)时,以$\mathscr{I}$k先验非空概率pk|k′作为条件,并针对不同$\mathscr{S}$k状态考虑$\mathscr{I}$k两种情况下对应的似然函数,以边缘化概率加权得$\mathscr{S}$k后验形式似然函数,反之亦如此.基于以上分析推导得信道占用状态的似然函数φk(yk|$\mathscr{S}$k)和脉冲噪声似然函数ψk(yk|$\mathscr{I}$k)分别为
| $ \begin{array}{*{20}{c}} {{\phi _k}\left( {{y_k}|{\mathscr{S}_k}} \right) = }\\ {\left\{ \begin{array}{l} {p_{k|{k^\prime }}}g\left( {{y_k}|{\mathscr{S}_k} = \left\{ {{x_k}} \right\},{\mathscr{T}_k} = \left\{ {{i_k}} \right\}} \right) + \\ \;\;\;\;\;\;\;\;\left( {1 - {p_{k|{k^\prime }}}} \right)g\left( {{y_k}|{\mathscr{S}_k} = \left\{ {{x_k}} \right\},{\mathscr{T}_k} = \emptyset } \right),\;\;\;\;{\mathscr{S}_k} = \left\{ {{x_k}} \right\}\\ {p_{k|{k^\prime }}}g\left( {{y_k}|{\mathscr{S}_k} = \emptyset ,{\mathscr{T}_k} = \left\{ {{i_k}} \right\}} \right) + \\ \;\;\;\;\;\;\;\;\left( {1 - {p_{k|{k^\prime }}}} \right)g\left( {{y_k}|{\mathscr{S}_k} = \emptyset ,{\mathscr{T}_k} = \emptyset } \right),{\mathscr{S}_k} = \emptyset \end{array} \right.} \end{array} $ | (17) |
| $ \begin{array}{*{20}{c}} {{\psi _k}\left( {{y_k}|{\mathscr{T}_k}} \right) = }\\ {\left\{ \begin{array}{l} {q_{k|k - 1}}g\left( {{y_k}|{\mathscr{S}_k} = \left\{ {{x_k}} \right\},{\mathscr{T}_k} = \left\{ {{i_k}} \right\}} \right) + \\ \;\;\;\;\;\;\;\left( {1 - {q_{k|k - 1}}} \right)g\left( {{y_k}|{\mathscr{S}_k} = \emptyset ,{\mathscr{T}_k} = \left\{ {{i_k}} \right\}} \right),\;\;\;\;{\mathscr{T}_k} = \left\{ {{i_k}} \right\}\\ {q_{k|k - 1}}g\left( {{y_k}|{\mathscr{S}_k} = \left\{ {{x_k}} \right\},{\mathscr{T}_k} = \emptyset } \right) + \\ \;\;\;\;\;\;\;\left( {1 - {q_{k|k - 1}}} \right)g\left( {{y_k}|{\mathscr{S}_k} = \emptyset ,{\mathscr{T}_k} = \emptyset } \right),\;\;\;\;{\mathscr{T}_k} = \emptyset \end{array} \right.} \end{array} $ | (18) |
根据贝叶斯序贯统计推理框架,基于贝叶斯法则对系统状态的后验概率分布进行估计.
对于$\mathscr{S}$k,利用似然函数及先验概率分布基于贝叶斯公式更新得后验概率分布为
| $ {f_{k|k}}\left( {{\mathscr{S}_k}|{y_{1:k}}} \right) = \frac{{{\varphi _k}\left( {{y_k}|{\mathscr{S}_k}} \right){f_{k|k - 1}}\left( {{\mathscr{S}_k}|{y_{1:k - 1}}} \right)}}{{\int {{\varphi _k}\left( {{y_k}|{\mathscr{S}_k}} \right){f_{k|k - 1}}\left( {{\mathscr{S}_k}|{y_{1:k - 1}}} \right)\delta {\mathscr{S}_k}} }} $ | (19) |
进一步根据伯努利随机有限集合定义推导$\mathscr{S}$k后验概率分布为[5]
| $ \left. \begin{array}{l} {q_{k|k}} = \frac{{{q_{k|k - 1}}\int {{\phi _k}\left( {{y_k}|\left\{ {{x_k}} \right\}} \right){t_{k|k - 1}}\left( {{x_k}} \right)d{x_k}} }}{{\left[ {\left( {1 - {q_{k|k - 1}}} \right){\varphi _k}\left( {{y_k}|\emptyset } \right) + {q_{k|k - 1}}\int {{\phi _k}} \left( {{y_k}|\left\{ {{x_k}} \right\}} \right){t_{k|k - 1}}\left( {{x_k}} \right)d{x_k}} \right]}}\\ {t_{k|k}}\left( {{x_k}} \right) = \frac{{{\phi _k}\left( {{y_k}|\left\{ {{x_k}} \right\}} \right){t_{k|k - 1}}\left( {{x_k}} \right)}}{{\int {{\phi _k}\left( {{y_k}|\left\{ {{x_k}} \right\}} \right){t_{k|k - 1}}\left( {{x_k}} \right)dx} }} \end{array} \right\} $ | (20) |
对于$\mathscr{I}$k,利用似然函数及先验概率分布基于贝叶斯公式更新得其后验概率分布为
| $ {f_{k|k}}\left( {{\mathscr{T}_k}|{y_{1:k}}} \right) = \frac{{{\psi _k}\left( {{y_k}|{\mathscr{T}_k}} \right){f_{k|{k^\prime }}}\left( {{\mathscr{T}_k}|{y_{1:{k^\prime }}}} \right)}}{{\int {{\psi _k}\left( {{y_k}\left| {{\mathscr{T}_k}} \right.} \right){f_{k|{k^\prime }}}\left( {{\mathscr{T}_k}|{y_{1:{k^\prime }}}} \right)\delta {\mathscr{T}_k}} }} $ | (21) |
进一步推导$\mathscr{I}$k后验概率分布为
| $ \left. \begin{array}{l} {p_{k|k}} = \frac{{{p_{k|{k^\prime }}}\int {{\psi _k}} \left( {{y_k}|\left\{ {{i_k}} \right\}} \right){r_{k|{k^\prime }}}\left( {{i_k}} \right)d{i_k}}}{{\left[ {\left( {1 - {p_{k|{k^\prime }}}} \right){\psi _k}\left( {{y_k}|\emptyset } \right) + {p_{k|{k^\prime }}}\int {{\psi _k}} \left( {{y_k}|\left\{ {{i_k}} \right\}} \right){r_{k|{k^\prime }}}\left( {{i_k}} \right)d{i_k}} \right]}}\\ {r_{k|k}}\left( {{i_k}} \right) = \frac{{{\psi _k}\left( {{y_k}|\left\{ {{i_k}} \right\}} \right){r_{k|{k^\prime }}}\left( {{i_k}} \right)}}{{\int {{\psi _k}} \left( {{y_k}|\left\{ {{i_k}} \right\}} \right){r_{k|{k^\prime }}}\left( {{i_k}} \right)di}} \end{array} \right\} $ | (22) |
针对上述后验概率分布公式中包含空间概率分布的复杂积分运算,采用基于重要性采样原理的粒子滤波理论实现算法以期减小运算复杂度[8].
针对$\mathscr{S}$k在非空情况下的空间概率分布tk(xk),建立一组数量N的粒子系统{εk(n), ωk(n)}n=1N,其中εk(n),ωk(n)为粒子n的状态(信号幅值)、权重,基于此,后验空间概率分布可近似表示为tk|k(xk)≈Σnωk|k(n)δ(ε-εk|k(n)),其中δ(·)为狄拉克函数.检测问题进一步转化为对εk|k(n), ωk|k(n)的序贯估计问题.具体来说,对粒子状态εk|k(n)的序贯更新采样依据占用信号的先验分布;而权重ωk|k(n)的更新依赖于所设计算法,涉及预测、更新2阶段.基于式(13),信道状态概率分布预测分为2项,则进一步将粒子等分2组进行权重预测为
| $ \omega _{k|k - 1}^{(n)} \propto \left\{ {\begin{array}{*{20}{l}} {{p_s}{q_{k - 1|k - 1}}\omega _{k - 1|k - 1}^{(n)},}&{n = 1,2, \cdots ,N/2}\\ {\frac{{{p_b}\left( {1 - {q_{k - 1|k - 1}}} \right)}}{N},}&{n = N/2 + 1, \cdots ,N} \end{array}} \right. $ | (23) |
其中ωk-1|k-1(n)为前时刻粒子权重.基于式(17)与式(20),推导权重更新公式为
| $ \begin{array}{*{20}{c}} {\omega _{k|k}^{(n)} \propto \omega _{k|k - 1}^{(n)}\left[ {{p_{k|{k^\prime }}}g\left( {{y_k}|{\mathscr{S}_k} = \left\{ {\varepsilon _{k|k}^{(n)}} \right\},{\mathscr{T}_k} = \{ \bar i\} } \right) + } \right.}\\ {\left. {\left( {1 - {p_{k|{k^\prime }}}} \right)g\left( {{y_k}|{\mathscr{S}_k} = \left\{ {\varepsilon _{k|k}^{(n)}} \right\},{\mathscr{T}_k} = \emptyset } \right)} \right]} \end{array} $ | (24) |
进一步对所得粒子权重进行归一化处理,则可对后验空间概率密度tk|k(xk)进行逼近.
针对$\mathscr{I}$k的空间概率分布rk|k(ik),建立一组数量为N的粒子系统{zk(n), υk(n)}n=1N,其中zk(n), υk(n)为粒子状态(脉冲噪声幅值)、权重.则需对粒子系统后验状态、权重zk|k(n), υk|k(n)进行序贯估计.其中,zk|k(n)更新采样基于噪声幅值分布$\mathscr{N}$(i, σi2);而υk|k(n)序贯更新同样包含预测、更新两阶段.具体地,基于噪声脉冲的独立特性,以直接等分形式预测权重,即υk|k′(n)=1/N;进而基于式(18)与式(22)推导权重更新公式为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{v}}_{k|k}^{(n)} \propto \mathit{\boldsymbol{v}}_{k|{k^\prime }}^{(n)}\left[ {{q_{k|k - 1}}g\left( {{y_k}|{\mathscr{S}_k} = \left\{ {{x_k}} \right\},{\mathscr{T}_k} = \left\{ {\mathit{\boldsymbol{z}}_{k|k}^{(n)}} \right\}} \right) + } \right.}\\ {\left. {\left( {1 - {q_{k|k - 1}}} \right)g\left( {{y_k}|{\mathscr{S}_k} = \emptyset ,{\mathscr{T}_k} = \left\{ {\mathit{\boldsymbol{z}}_{k|k}^{(n)}} \right\}} \right)} \right]} \end{array} $ | (25) |
归一化处理后,以该后验粒子系统对空间概率密度进行逼近,即
通过利用离散粒子系统逼近复杂的后验空间概率分布,将包含空间概率分布的积分运算变为求和运算;并通过对粒子状态及权重进行预测与更新实现算法,极大降低了算法复杂度.
判决阶段,设置判决门限γ与η,若信道占用的后验概率估计值qk|k大于判决门限γ则判为信道占用;若脉冲噪声后验存在概率估计值pk|k大于判决门限η则判为脉冲噪声存在.根据脉冲噪声存在情况下的后验空间概率分布粒子系统,以粒子系统权重中心作为脉冲噪声估计幅值,表示为
| $ {{\hat i}_k} = \sum\limits_{n = 1}^N {v_k^{(n)}} z_k^{(n)} $ | (26) |
所提联合检测算法旨在解决信道中由脉冲噪声引起的空闲信道检测效果下降问题,数值仿真以脉冲噪声与信号的幅值比和背景噪声信噪比作为自变量.参数设置:检测时隙内的采样点数目M=20;信道占用状态转移概率为pb=0.8,ps=0.2.
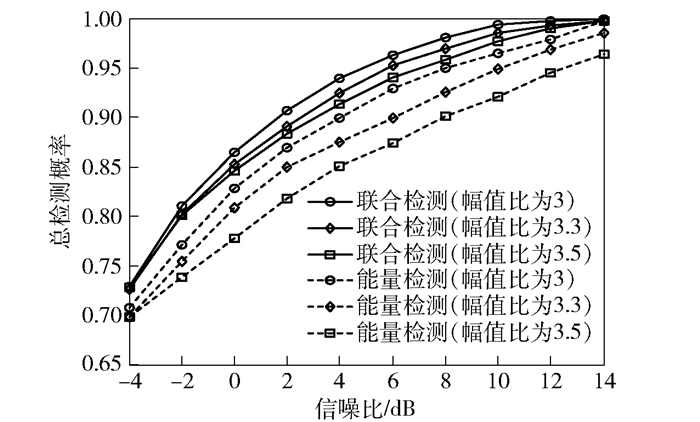
对于所提算法的空闲信道检测精度,考虑到漏检将导致不同用户/设备间的数据碰撞;而虚警将造成宝贵传输资源的浪费.故首先对总检测概率(Pr{H1|H1}p(H1)+Pr{H0|H0}p(H0))进行仿真分析.综合权衡检测概率与虚警概率影响,设置等分的判决门限γ=η=0.5,结果如图 1所示.其中实线为所提联合检测算法性能,虚线为能量检测(ED)方法性能.所提算法在上述含有脉冲噪声的电磁环境中与传统能量检测相比总检测概率有明显的提升.在脉冲噪声幅值均值为信号幅值的3.5倍、空闲信道检测概率为0.9时检测性能提升约6 dB.
|
图 1 空闲信道总检测概率对比 |
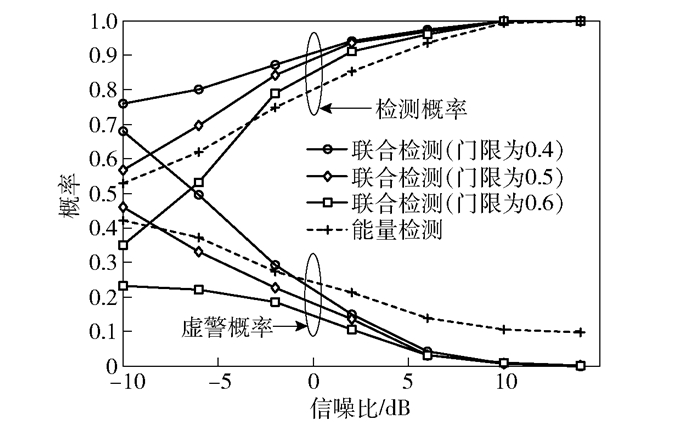
进一步分析不同判决门限下的检测概率与虚警概率.仿真设置脉冲噪声幅值均值为信号幅值的3.5倍,并分别设置信道判决门限γ为0.4/0.5/0.6,结果如图 2所示.能量检测在该场景下虚警概率明显上升,而所提联合检测方案在检测概率好于能量检测的同时,能有效对抗脉冲噪声带来的虚警影响,信噪比大于10 dB时,所提算法虚警概率相较于能量检测减小10倍以上.此外,随着判决门限γ的提高,所提算法检测概率与虚警概率均下降,在实际检测问题中,可依据不同的任务需求具体设置判决门限,从而实现不同的检测功能.
|
图 2 不同判决门限下检测概率与虚警概率对比 |
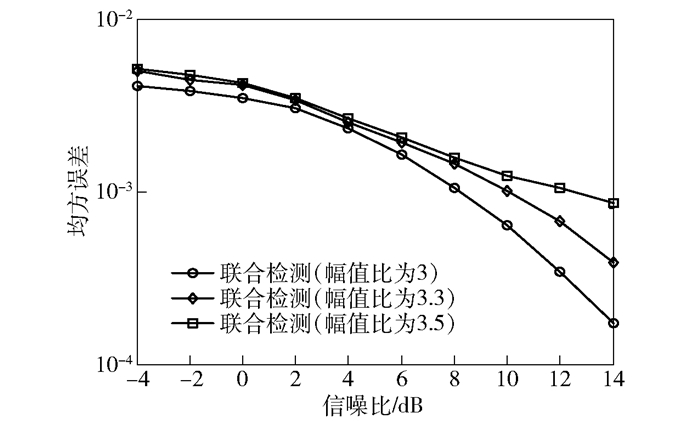
除提升空闲信道检测精度外,所提算法可对脉冲噪声进行联合估计,仿真结果如图 3所示.所提算法对脉冲噪声的出现以及幅值可进行较为准确的估计;随着脉冲噪声幅值均值的降低,其所带来的影响也将降低,体现为幅值估计均方误差(MSE,mean square error)的降低.通过准确估计脉冲噪声,一方面降低其对空闲信道检测的影响;另一方面也提供了额外的信道状态信息.
|
图 3 脉冲噪声幅值估计均方误差 |
针对未来智能电网变电站的电磁脉冲噪声环境下的高可靠性空闲信道检测难题,提出了一种基于贝叶斯统计推理框架的全新空闲信道联合检测方法.创造性地把信道占用状态和脉冲噪声建模为两个伯努利随机有限集合,通过挖掘利用系统状态间的嵌套耦合关系并充分利用已知的先验信息,基于贝叶斯理论完成对两系统状态的序贯联合估计.粒子滤波方法降低了算法复杂度.数值仿真结果显示,新方法与传统方法相比在显著提升空闲信道检测精度的同时将脉冲噪声的出现及其幅值纳入估计过程,为后续资源分配提供更加全面的链路信息.
| [1] |
Peter A O, Ng C K, Noordin N K. Power line communication (PLC) impulsive noise mitigation:a review[J]. Journal of Information Engineering and Applications, 2014, 4(10): 86-104. |
| [2] |
Ramachandran I, Roy S. Clear channel assessment in energy-constrained wideband wireless networks[J]. IEEE Wireless Communications, 2007, 14(3): 70-78. DOI:10.1109/MWC.2007.386615 |
| [3] |
Li B, Li S H, Nallanathan A, et al. Deep sensing for next-generation dynamic spectrum sharing:more than detecting the occupancy state of primary spectrum[J]. IEEE Transactions on Communications, 2015, 63(7): 2442-2457. DOI:10.1109/TCOMM.2015.2443041 |
| [4] |
Wang H S, Moayeri N. Finite-state markov channel:a useful model for radio communication channels[J]. IEEE Transactions on Vehicular Technology, 1995, 44(1): 163-171. DOI:10.1109/25.350282 |
| [5] |
Ma J, Li G Y, Juang B H. Signal processing in cognitive radio[J]. The Proceedings of IEEE, 2009, 97(5): 805-823. DOI:10.1109/JPROC.2009.2015707 |
| [6] |
Ristic B, Vo B T, Vo B N, et al. A tutorial on Bernoulli filters:theory, implementation and applications[J]. IEEE Transactions on Signal Processing, 2004, 61(13): 3406-3430. |
| [7] |
Li B, Zhao C L, Sun M W, et al. Spectrum sensing for cognitive radios in time-variant flat fading channel:a joint estimation approach[J]. IEEE Transactions on Communications, 2014, 62(8): 2665-2680. DOI:10.1109/TCOMM.2014.2325835 |
| [8] |
Djuric P M, Kotecha J H, Zhang J Q, et al. Particle filtering[J]. IEEE Signal Processing Magazine, 2003, 20(5): 19-38. DOI:10.1109/MSP.2003.1236770 |



