2. 南京航空航天大学 电磁频谱空间认知动态系统工信部重点实验室, 南京 211106
北斗B1频点信号采用二次编码结构,而二次编码使用的NH(Neumann-Hoffman)码会发生比特跳变,导致接收机捕获性能降低,对此,提出一种基于伪码与多普勒频率分离的北斗信号捕获算法.该算法将接收信号分为两路,利用延迟差分运算和测距码的双极性分别对两路信号进行处理,消除了NH码比特跳变带来的影响.在此基础上使用匹配滤波器捕获码相位,使用快速傅里叶变换搜索多普勒频移,实现了码相位和多普勒频移的同时捕获.仿真结果表明,提出的算法成功捕获到了NH码跳变的信号,且在相同虚警率下灵敏度相比部分匹配滤波和快速傅里叶变换算法约有1.03 dB的提升.
2. Key Laboratory of Dynamic Cognitive System of Electromagnetic Spectrum Space(Ministry of Industry and Information Technology), Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China
Beidou B1 frequency signal using the secondary encoding structure, bit-flipping of Neumann-Hoffman (NH) codes used for secondary encoding leads to a decrease in receiver acquisition performance. Aiming at this problem, a Beidou signal acquisition algorithm based on pseudocode and Doppler frequency separation is proposed. The algorithm divides the received signal into two paths, and uses the delay difference operation and the bipolarity of the ranging code to process the two signals respectively, thus eliminating the influence of the bit hopping of the NH code. Based on this, the matched filter is used to capture the phase of the code and the fast Fourier transformation is used to search for the Doppler frequency. Capturing the phase and the Doppler frequency at the same time is realized. Finally, the simulation results show that the proposed algorithm successfully captures the signal with bit-flipping. Compared to partial matched filtering-fast Fourier transformation algorithm, the sensitivity is 1.03 dB increased under the same false alarm rate.
信号捕获是卫星接收机的关键技术之一,它的主要目的是得到接收到卫星信号的多普勒频移和伪随机码相位延迟,以实现本地产生的载波和码相位与卫星同步,进行后续的解算[1-2].由此可见,信号捕获是接收机中重要的一个步骤,捕获速度直接影响了接收机的性能[3].北斗D1和D2导航电文数据比特跳变时间分别是20 ms和2 ms,且D1导航电文上调制了速率为1 kbit/s的NH码,故每经过1 ms就可能发生一次比特跳变,严重影响了接收机信号的捕获质量[4].姚如贵等[5]使用快速傅里叶变换(FFT, fast Fourier transformation)将信号由时域变换到频域进行处理,提高了捕获速度但运算量大且灵敏度不高.罗海坤等[6]将匹配滤波器和FFT算法结合起来改善了匹配滤波器在捕获多普勒频移时的不足,但是受比特跳变干扰严重.王嘉宁等[7]进一步改进了部分匹配滤波和FFT(PMF-FFT, partial matched filters combined with FFT)模型,消除了符号跳变的影响,但是对系统资源和性能的要求较高.韩志凤等[8]考虑了符号跳变对捕获的影响,引入差分相关的捕获算法消除捕获码相位时NH码跳变的影响,但在搜索多普勒频移时未考虑NH码跳变的情况,导致捕获性能下降.
笔者提出了一种基于伪码与多普勒频率分离的捕获算法,在不剥离NH码的条件下使用差分运算消除比特跳变对码相位捕获的影响,利用C码的双极性消除比特跳变对搜索多普勒频移的影响,实现了码相位和多普勒频移的独立捕获.
1 北斗B1频点信号结构北斗系统采用码分多址的调制方式,首先将导航电文用伪随机码进行扩频,然后将扩频后的信号调制到载波上,最后卫星再把调制后的载波信号发射出去.北斗B1频点信号由I、Q两支路正交调制到载波上构成,信号的表达式为
| $ \begin{array}{*{20}{c}} {{S^j}(t) = {A_{\rm{I}}}C_{\rm{I}}^j(t)D_{\rm{I}}^j(t)\cos \left( {2{\rm{ \mathsf{ π} }}{f_0} + {\varphi ^j}} \right) + }\\ {{A_{\rm{Q}}}C_{\rm{Q}}^j(t)D_{\rm{Q}}^j(t)\sin \left( {2{\rm{ \mathsf{ π} }}{f_0} + {\varphi ^j}} \right)} \end{array} $ | (1) |
其中:I、Q为两条不同的支路,j为卫星的编号,A为信号的振幅,C为北斗的测距码,D为数据码,φ为载波初相,f0为载波频率.北斗B1频点载波频率为1 561.098 MHz.
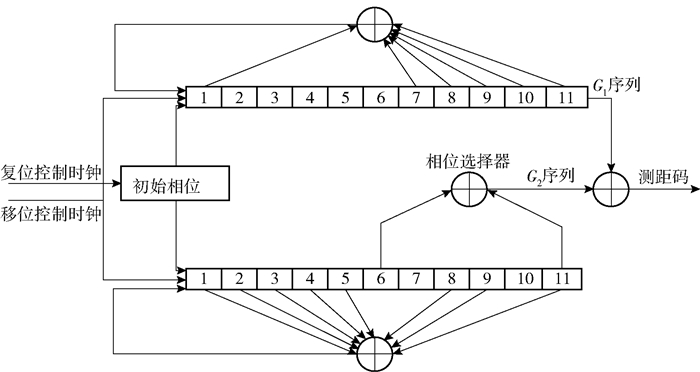
北斗系统中Q路信号只有授权用户能使用,故只讨论I路信号. I路测距码本质是码长为2 046码片、码率为2.046 Mchip/s的金码.金码自身有良好的自相关性,信号捕获正是利用了其这一性质来计算测距码的码相位的.金码是由G1和G2两个线性序列模二和生成的,其表达式如下:
| $ {G_1}(X) = 1 + {X^7} + X + {X^9} + {X^{10}} + X + {X^{11}} $ | (2) |
| $ {G_2}(X) = 1 + X + {X^2} + {X^3} + {X^4} + {X^5} + {X^8} + {X^9} + {X^{11}} $ | (3) |
通过G1和G2序列模二和能生成长度为2 047码片的金码,将其截去最后一位就得到了北斗系统的测距码.测距码发生器如图 1所示.
|
图 1 测距码发生器 |
假设接收机收到的北斗Ⅰ路信号为
| $ S(t) = \sqrt {2P} C(t - \tau )D(t - \tau )\cos \left( {{\omega _s}t + \varphi } \right) + n(t) $ | (4) |
其中:P为信号功率,τ为接收机信号延迟,ωs为考虑了多普勒频移的载波频率,n(t)为高斯白噪声.假设在ts时刻发生了比特跳变,同时为了分析方便省略噪声,则接收信号表示为
| $ S(t) = \sqrt {2P} C(t - \tau )P(t - \tau )\cos \left( {{\omega _s}t + \varphi } \right) $ | (5) |
其中P(t-τ)在t≤ts时为1,在t≥ts时为-1.
2 比特跳变对传统信号捕获的影响使用传统信号捕获方法的接收机接收到形如式(5)的信号后,将其与正交的两路本地载波混频以剥离载波,再与本地复制的测距码Cr(t)做相关运算得到I、Q两路结果,其中Ⅰ路为[9]
| $ \begin{array}{*{20}{c}} {{Y_1}(t) = \int_{t - N{T_{\rm{c}}}}^t {\frac{{\sqrt {2P} }}{2}C(\theta - \tau ){C_r}\left( {N{T_{\rm{c}}} - t + \theta } \right)x} \times }\\ {P(\theta - \tau )\cos \left( {\Delta \omega \theta + {\varphi _0}} \right){\rm{d}}\theta } \end{array} $ | (6) |
其中:N为采样点数,Tc为采样间隔,θ为积分变量,Δω=ωs-ω0为本地载波与接收信号载波的差.当测距码相位对齐时C(θ-τ)Cr(NTc-t+θ)=1,假设比特跳变发生在Ns=
| $ \begin{array}{*{20}{c}} {{Y_{\rm{I}}}(t) = \frac{{\sqrt {2P} }}{{\Delta \omega }}\sin \left( {\frac{1}{4}\Delta \omega N{T_{\rm{c}}}} \right)\{ \cos [\Delta \omega (t - }\\ {\left. {\left. {\left. {\frac{3}{4}N{T_{\rm{c}}}} \right) + {\varphi _0}} \right] - \cos \left[ {\Delta \omega \left( {t - \frac{1}{4}N{T_{\rm{c}}}} \right) + {\varphi _0}} \right]} \right\}} \end{array} $ | (7) |
类似地,Q路信号可以表示为
| $ \begin{array}{*{20}{c}} {{Y_{\rm{Q}}}(t) = \frac{{\sqrt {2P} }}{{\Delta \omega }}\sin \left( {\frac{1}{4}\Delta \omega N{T_c}} \right)\{ \sin [\Delta \omega (t - }\\ {\left. {\left. {\left. {\frac{1}{4}N{T_{\rm{c}}}} \right) + {\varphi _0}} \right] - \sin \left[ {\Delta \omega \left( {t - \frac{3}{4}N{T_{\rm{c}}}} \right) + {\varphi _0}} \right]} \right\}} \end{array} $ | (8) |
将I、Q两路信号平方求和可以得到与门限进行比较的值,化简后有
| $ \begin{array}{*{20}{c}} {{R^2} = Y_{\rm{I}}^2(t) + Y_{\rm{Q}}^2(t) = \frac{1}{4}P{N^2}T_{\rm{c}}^2\sin \left( {\frac{1}{4}\Delta \omega N{T_{\rm{c}}}} \right) \times }\\ {\left[ {1 - \cos \left( {\frac{1}{2}\Delta \omega N{T_{\rm{c}}}} \right)} \right]} \end{array} $ | (9) |
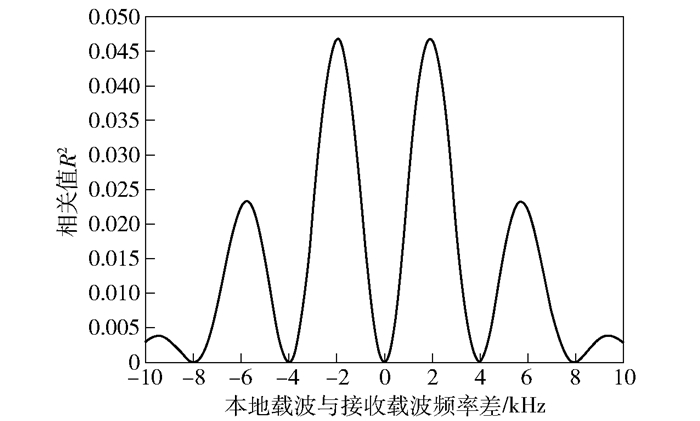
在0.5N码片即数据中点发生比特跳变时,相关值随多普勒频移变化曲线如图 2所示.
|
图 2 比特跳变对捕获的影响 |
由图 2可以看出,码片对齐时检测变量的值受Δω影响,且Δω=0时R2=0.这表明在正确的码片相位和多普勒频移估计的情况下,检测变量主峰完全消失,两侧出现2个较小峰值,严重影响了捕获的性能.
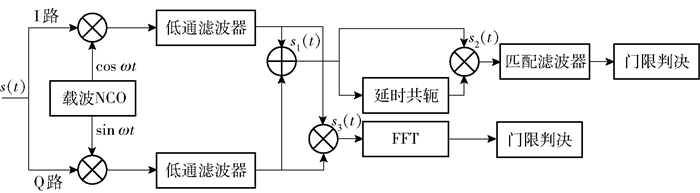
3 伪码与多普勒频率分离的捕获算法针对比特跳变影响捕获性能这一问题,将混频后的接收信号分为S1(t)和S3(t)两路[10],其中,S1(t)利用其与自身延迟共轭相乘消除比特跳变和载波频率的影响,S3(t)利用测距码的双极性消除比特跳变和伪随机码的影响.经过处理的2路信号一路通过匹配滤波器搜索码相位,另一路利用FFT搜索多普勒频移,实现了码相位和多普勒频移的同时分离捕获,且两支路相互独立,如图 3所示[11].
|
图 3 伪码与多普勒频率分离捕获算法 |
接收信号S(t)形式如式(5),该信号与本地载波进行混频后可得
| $ {S_1}(t) = \frac{{\sqrt {2P} }}{2}C(t - \tau )P(t - \tau ){{\rm{e}}^{ - {\rm{j}}\left( {\Delta \omega t + {\varphi _0}} \right)}} $ | (10) |
S1(t)与其延迟一个码片时间Tc后的共轭相乘得到
| $ \begin{array}{*{20}{c}} {{S_2}(t) = {S_1}(t)\overline {{S_1}\left( {t - {T_{\rm{c}}}} \right)} = }\\ {\frac{P}{2}C(t - \tau )C\left( {t - \tau - {T_{\rm{c}}}} \right)P(t - \tau )P\left( {t - \tau - {T_{\rm{c}}}} \right){{\rm{e}}^{{\rm{j}}\Delta \omega {T_{\rm{c}}}}}} \end{array} $ | (11) |
由式(11)可以看出,P(t)的值为1或-1,若发生比特跳变P(t-τ)P(t-τ-Tc)的值为-1,其余时刻值均为1.经前文分析一个C码周期1 ms最多存在一次比特跳变,所以经过处理后的信号仅有跳变时刻的一个码片会受影响,捕获性能得到提升[12].同时,ejΔωTc是一个常数,故只需要对S2(t)进行码相位一维搜索即可,找到准确的码相位后再对多普勒频率进行搜索,完成信号捕获.
下面采用匹配滤波器来捕获码相位.由于对输入信号进行了处理,本地存储的C码Cr(NTc-t)也需要相同的处理:
| $ {C_{{\rm{loc}}}}\left( {N{T_{\rm{c}}} - t} \right) = {C_r}\left( {N{T_{\rm{c}}} - t} \right)\overline {{C_r}\left( {N{T_{\rm{c}}} - t - {T_{\rm{c}}}} \right)} $ | (12) |
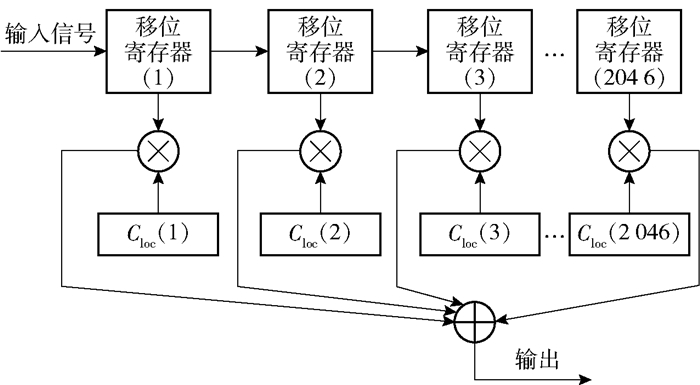
经处理后的本地码每个码片值决定了匹配滤波器中每个寄存器的赋值.所使用的匹配滤波器结构如图 4所示.
|
图 4 匹配滤波器结构 |
图 4中Cloc(n)表示处理后的本地码第n个码片,信号S2(t)进入该匹配滤波器做相关运算可以得到
| $ \begin{array}{*{20}{c}} {{R_1} = \int_{t - N{T_{\rm{c}}}}^t {\frac{P}{2}C(\theta - \tau )C\left( {\theta - \tau - {T_{\rm{c}}}} \right)P(\theta - \tau )} \times }\\ {P\left( {\theta - \tau - {T_{\rm{c}}}} \right){C_{{\rm{loc}}}}\left( {N{T_{\rm{c}}} - t} \right){{\rm{e}}^{{\rm{j}}\Delta \omega {T_{\rm{c}}}}}{\rm{d}}\theta = }\\ {\int_{t - N{T_{\rm{c}}}}^t {\frac{P}{2}C(\theta - \tau )C\left( {\theta - \tau - {T_{\rm{c}}}} \right){C_r}\left( {N{T_{\rm{c}}} - t} \right)} \times }\\ {{C_r}\left( {N{T_{\rm{c}}} - t - {T_{\rm{c}}}} \right)P(\theta - \tau )P\left( {\theta - \tau - {T_{\rm{c}}}} \right){{\rm{e}}^{{\rm{j}}\Delta \omega {T_{\rm{c}}}}}{\rm{d}}\theta } \end{array} $ | (13) |
将式(13)计算结果R1与预设门限比较,若大于门限值则视伪码相位捕获成功[13].当接收信号与本地码相位对齐时可以得C(θ-τ)C(θ-τ-T)×Cr(NTc-t)Cr(NTc-t-Tc)的值为1,P(θ-τ)P(θ-τ-Tc)在发生比特跳变的一个码片时间内值为-1,其余时间均为1.此时相关结果为
| $ \begin{array}{*{20}{c}} {R = \frac{P}{2}{{\rm{e}}^{{\rm{j}}\Delta \omega {T_{\rm{c}}}}}\int_{t - N{T_{\rm{c}}}}^t P (\theta - \tau )P\left( {\theta - \tau - {T_{\rm{c}}}} \right){\rm{d}}\theta = }\\ {\frac{{N - 2}}{2}P{T_{\rm{c}}}{{\rm{e}}^{{\rm{j}}\Delta \omega {T_{\rm{c}}}}}} \end{array} $ | (14) |
对于多普勒频移的搜索将由S3(t)所在支路进行.假设图 3中经过混频滤波后的I路信号为SI(t),则
| $ \begin{array}{*{20}{c}} {{S_3}(t) = {S_{\rm{I}}}(t){S_{\rm{Q}}}(t) = }\\ {\frac{P}{4}{C^2}(t - \tau ){P^2}(t - \tau )\sin (2\Delta \omega t + 2\varphi )} \end{array} $ | (15) |
由前文可知C(t)和P(t)值均为1或-1,故S3(t)可化简为[14]
| $ {S_3}(t) = \frac{P}{4}\sin (2\Delta \omega t + 2\varphi ) $ | (16) |
由式(16)可见,信号已经消除了NH码跳变带来的影响,利用FFT对S3(t)进行离散傅里叶变换,将得到的幅值与预设门限进行比较,若大于门限,则视为捕获成功,且相应幅值所对应频率点为捕获到的多普勒频移的2倍.
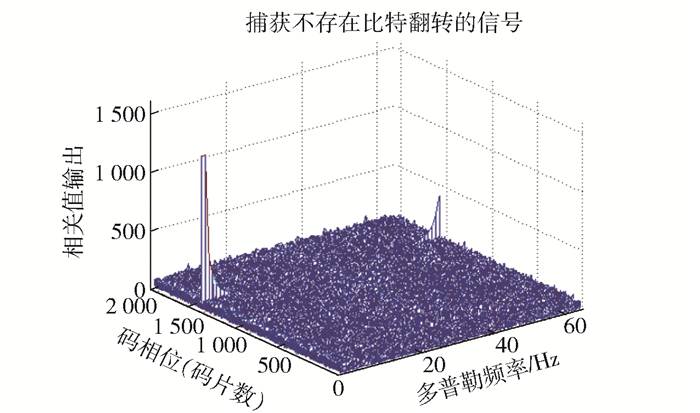
4 仿真分析为验证所提算法的捕获性能,以北斗1号卫星所产生伪码进行捕获过程仿真.捕获中生成的伪码速率为2.046 Mchip/s,码长2 046码片,信号采样率设置为2.046 MHz. NH码速率为1 KB/s且在0.5 ms发生翻转,正确的码相位为第1 531码片,加入的多普勒频移设为500 Hz,初始相位为0,载噪比为45 dB,虚警率设为pfa=0.01.若接收信号不存在比特跳变,使用PMF-FFT算法进行捕获的结果如图 5所示.
|
图 5 PMF-FFT捕获结果 |
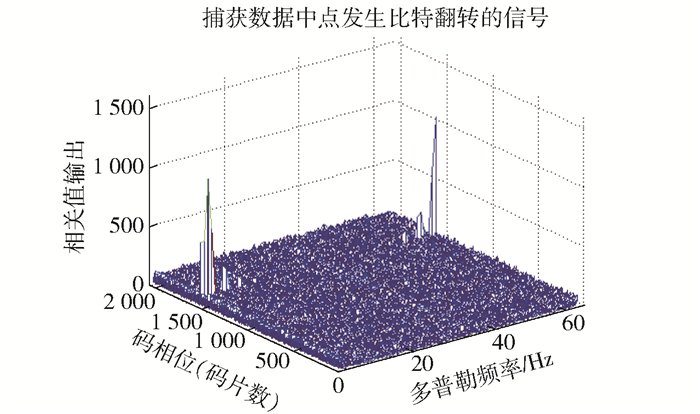
PMF-FFT算法成功捕获到了信号.若信号在0.5 ms处发生翻转,分别用PMF-FFT算法和文献[8]算法以及所提算法捕获同一个信号,结果如图 6~图 10所示.
|
图 6 PMF-FFT算法无法成功捕获 |

|
图 7 文献[8]中算法捕获0.5 ms时NH码翻转的信号码相位结果 |
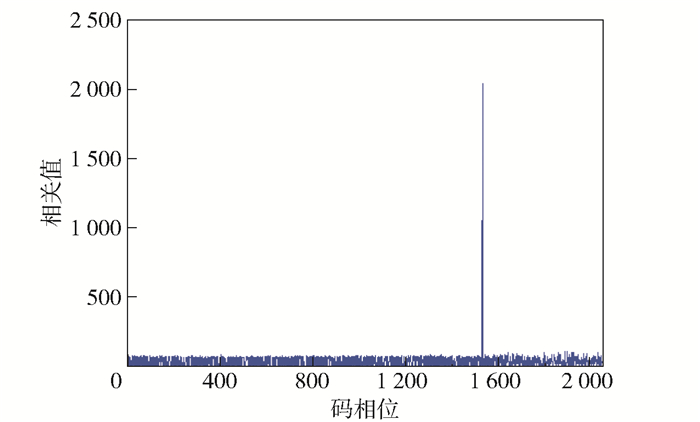
|
图 8 本文算法捕获0.5 ms时NH码翻转的信号码相位结果 |
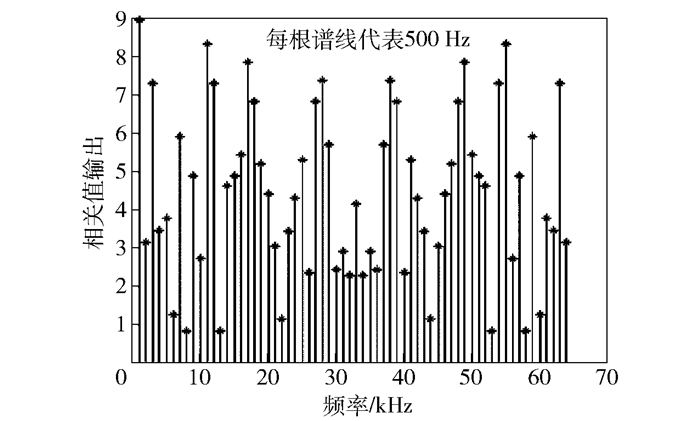
|
图 9 文献[8]中算法捕获0.5 ms时NH码翻转的信号多普勒频移结果 |
|
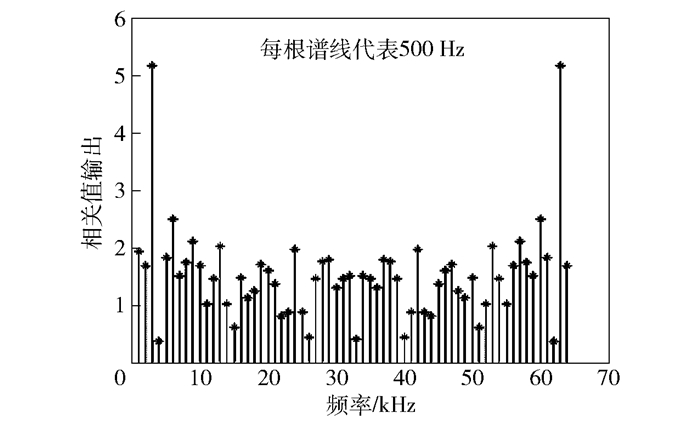
图 10 本文算法捕获0.5 ms时NH码翻转的信号多普勒频移结果 |
由图 6可见,在NH码跳变的情况下, PMF-FFT算法已经无法捕获到信号.由于比特跳变的干扰,检测值在正确的码相位及多普勒频率位置的主峰消失,两侧出现2个较小的峰值,与前文的理论分析结果相吻合. 图 7和图 8分别为文献[8]算法和所提算法捕获码相位结果,证明文献[8]算法和所提算法克服了比特跳变带来的影响,成功捕获到信号的码相位,码片位置为1531与预设值一致. 图 9为文献[8]中算法捕获多普勒频移结果,在捕获多普勒频移时,由于文献[8]算法未考虑NH码跳变,故捕获性能较差,主峰不明显. 图 10为所提算法捕获多普勒频移结果,该算法采用64点FFT运算,经过计算得每根谱线代表的频率为2.046 MHz/64=500 Hz.第3条谱线代表 1 000 Hz,是预设多普勒频率的2倍,与前文理论推导一致,故所提算法正确捕获到了多普勒频移.
算法灵敏度的对比方法参考文献[7],令多普勒频移均匀分布,在各个多普勒频移下90%检测概率对应的信号载噪比作为捕获灵敏度,对比结果如图 11所示.对于90%检测概率,所提算法在存在比特跳变的情况下比PMF-FFT算法灵敏度提高1.03 dB.

|
图 11 灵敏度对比 |
在使用现场可编程门阵列实现时,算法消耗的硬件资源也是需要考虑的因素.将3种算法消耗的资源进行对比,结果如表 1所示.
|
|
表 1 算法实现复杂度对比 |
由表 1的对比可见,所提算法在适当增加系统复杂度的条件下,克服了比特跳变的干扰,并且实现了码相位和多普勒频移的直接独立捕获.
5 结束语在捕获北斗B1频点信号的过程中,比特跳变的存在严重影响了接收机捕获性能.笔者提出一种伪码与多普勒频率分离捕获算法,消除了比特跳变带来的干扰,并且实现码相位和多普勒频移同时分离捕获.仿真结果表明,所提算法成功捕获到了北斗1号卫星存在比特跳变的信号,且在虚警率同为0.01的条件下,检测灵敏度比PMF-FFT算法有1.03 dB的提升.
| [1] |
李文刚, 黄鑫磊, 刘龙伟. 低信噪比环境下的长码捕获新算法[J]. 西安电子科技大学学报, 2013, 40(4): 29-36. Li Wengang, Huang Xinlei, Liu Longwei. New long code acquisition algorithms in low SNR environment[J]. Journal of Xi'an University of Electronic Science and Technology, 2013, 40(4): 29-36. DOI:10.3969/j.issn.1001-2400.2013.04.005 |
| [2] |
郑伦贵, 尤政, 张高飞, 等. 基于非相干积分的GNSS弱信号捕获[J]. 清华大学学报(自然科学版), 2014, 54(6): 794-798. Zheng Lungui, You Zheng, Zhang Gaofei, et al. GNSS weak signal acquisition based on incoherent integral[J]. Journal of Tsinghua University (Natural Science Edition), 2014, 54(6): 794-798. |
| [3] |
Jin Tian, Lu Fangyao, Liu Yang, et al. Double differentially coherent pseudo random noise code acquisition method for code-division multiple access system[J]. IET Signal Processing, 2013, 7(7): 587-597. DOI:10.1049/iet-spr.2012.0020 |
| [4] |
Juang Jyhching, Tsai Chiuteng, Chen Yuhsuan. Development of a PC-based software receiver for the reception of Beidou navigation satellite signals[J]. Journal of Navigation, 2013, 66(5): 701-718. DOI:10.1017/S0373463313000271 |
| [5] |
姚如贵, 冯泽明, 赵雨, 等. 基于FFT的时频并行捕获算法研究[J]. 西北工业大学学报, 2013, 31(3): 446-450. Yao Rugui, Feng Zeming, Zhao Yu, et al. Time-frequency parallel acquisition algorithm based on FFT[J]. Journal of Northwest Polytechnic University, 2013, 31(3): 446-450. DOI:10.3969/j.issn.1000-2758.2013.03.028 |
| [6] |
罗海坤, 王永庆, 罗雨, 等. PMF-FFT算法中码多普勒频率影响的分析及补偿[J]. 北京理工大学学报, 2013, 33(11): 1176-1182. Luo Haikun, Wang Yongqing, Luo Yu, et al. Analysis and compensation of code Doppler frequency influence in PMF-FFT algorithm[J]. Journal of Beijing University of Technology, 2013, 33(11): 1176-1182. DOI:10.3969/j.issn.1001-0645.2013.11.015 |
| [7] |
王嘉宁, 廉保旺, 吴鹏. 基于频域符号相关的北斗信号捕获新算法[J]. 西北工业大学学报, 2016, 34(5): 867-873. Wang Jianing, Lian Baowang, Wu Peng. A new Beidou signal acquisition algorithm based on frequency domain symbol correlation[J]. Journal of Northwest Polytechnic University, 2016, 34(5): 867-873. DOI:10.3969/j.issn.1000-2758.2016.05.020 |
| [8] |
韩志凤, 刘建业, 李荣冰, 等. 基于差分相关积分的北斗弱信号快速捕获方法[J]. 中国惯性技术学报, 2016, 24(6): 815-820. Han Zhifeng, Liu Jianye, Li Rongbing, et al. Fast acquisition method of Beidou weak signal based on differential correlation integral[J]. Chinese Journal of Inertial Technology, 2016, 24(6): 815-820. |
| [9] |
丁继成, 刘爱萌, 赵琳. 一种克服NH码调制影响的北斗卫星信号捕获方法[J]. 遥测遥控, 2015, 36(1): 58-62. Ding Jicheng, Liu Aimeng, Zhao Lin. A method of Bei-dou satellite signal acquisition to overcome the influence of NH code modulation[J]. Telemetry and Remote Control, 2015, 36(1): 58-62. DOI:10.3969/j.issn.2095-1000.2015.01.010 |
| [10] |
Smidt J, Ozafrain S, Roncagliolo P A, et al. New technique for weak GNSS signal acquisition[J]. IEEE Latin America Transactions, 2014, 12(5): 889-894. DOI:10.1109/TLA.2014.6872901 |
| [11] |
何智力, 徐颖, 袁洪, 等. 一种基于二维细化的自适应信号捕获算法[J]. 电子与信息学报, 2014, 36(10): 2450-2455. He Zhili, Xu Ying, Yuan Hong, et al. Based on two-dimensional refinement adaptive signal acquisition algorithm[J]. Journal of Electronics and Information, 2014, 36(10): 2450-2455. |
| [12] |
吴皓威, 刘远, 杨力生, 等. 基于差分判决的GPS弱信号长比特相干捕获算法[J]. 华中科技大学学报(自然科学版), 2013, 41(7): 42-46. Wu Haowei, Liu Yuan, Yang Lisheng, et al. Longbit coherent acquisition algorithms for GPS weak signals based on differential decision[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2013, 41(7): 42-46. |
| [13] |
严昆仑, 章红平, 张提升, 等. NH码对新一代GNSS信号捕获跟踪的影响[J]. 武汉大学学报(信息科学版), 2015, 40(5): 682-687. Yan Kunlun, Zhang Hongping, Zhang Tisheng, et al. The influence of NH codes on the acquisition and tracking of new generation GNSS signals[J]. Journal of Wuhan University (Information Science Edition), 2015, 40(5): 682-687. |
| [14] |
李新山, 郭伟. 基于平均相关和差分相干累积的微弱GPSC/A码信号精密捕获算法[J]. 通信学报, 2015, 36(5): 112-119. Li Xinshan, Guo Wei. Accurate acquisition algorithm of weak GPS C/A code signal based on mean correlation and differential coherent accumulation[J]. Journal of Communications, 2015, 36(5): 112-119. |


